2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, Liaoning, China
Steel Reinforced Ultra High Strength Concrete-Reinforced Concrete (SRUHSC-RC) structures make full use of the respective performance advantages of steel and ultra-high strength concrete to optimize the combination. Compared with traditional concrete structure, it has the advantages of small size, light weight, convenient construction, good mechanical performance, good crack resistance and so on. Compared with steel structure, it has the advantages of large stiffness, small amount of steel, good fatigue crack resistance and so on. Therefore, it has a broad application prospect in major engineering[1]. In particular, the development of various admixtures has promoted the development of ultra-high strength concrete manufacturing technology and the development of mixed structures[2]. In general, its definition of 28-day compressive strength of ultra-high strength concrete is determined by standard 150 mm×150 mm specimens above 100 MPa[2]. Compared with ordinary concrete, ultra-high strength concrete has excellent compressive properties, excellent durability and economic benefits[2]. Hence, super-high-strength concrete has been widely applied in composite structures and it is highly necessary to improve the earthquake-resistance performance of SRUHSC-RC structures.
The seismic behavior of the hybrid joint which dominates the whole structural system has become one of the critical problems for seismic design[3]. The research of steel-concrete frame structure joints was mainly focused on the ordinary concrete. Hanson and Connor[4] first proposed a quantitative definition of combined shearing. Paulay et al.[5] suggested the qualitative mechanisms of shear-resistance which consist of diagonal compression strut. After that, numerous researchers have subsequently carried out RC joint specimens test to investigate the critical influential factors for the seismic performance of the RC joints [6-13]. In general, it has been founded that joint shear strength has been coherently related to the compressive strength of concrete, joint transverse reinforcement and column axial load. Kim et al.[14] collected an extensive database of RC joint test specimens exhibiting joint shear failure. The test parameters of shear performance of joints were grouped according to material properties, joint plate geometry, reinforcement constraints, column axial load and reinforcement bonding conditions[15]. They also found that steel combined to RC structures can improve structural ductility. In addition, Sheikh et al.[16] conducted tests on internal reinforced concrete column-steel beam joints and formulated design guidelines for composite RCS frame beam-column bending moment connections. Parra-Montesinos et al.[17] studied the behavior of joints from the aspects of shear strength and deformation, stiffness degradation, strain and stress of stirrups and steel webs at the core area of joints by testing nine external RCS specimens. Chen and Lin[18] also conducted cyclic loading tests on five large-scale cruciform beam-column joint specimens. The experimental study mainly focused on the shear strength. In addition, their proposed models have ignored the effect of axial compression force on shearing resistance. The model for the strength prediction indicated large discrepancies between the predicted and experimental data. The high brittleness of ultra-high strength concrete determines its difference from ordinary concrete[19]. Its stress-strain curve is steeper than that of ordinary concrete, and there is "snap back" phenomenon[20]. The value of softening coefficient of compressive strength to main tensile strain is different from that of ordinary concrete[1]. Therefore, an experimental investigation was undertaken to compensate for the information on the plastic mechanical properties of SRUHSC exterior connection.
In this paper, low cycle reciprocation tests of eleven SRUHSC-RC frame exterior connections were conducted to study seismic behavior of the joint. The hysteretic behavior, ductility, energy dissipation property, strength degradation, stiffness degradation, strains of stirrups and steel web at the core area of joints were analyzed. Furthermore, the parameter sensitivity analysis was carried out for the key influencing factors such as axial compression ratio, stirrup ratio and steel ratio.
1 Experimentation Scheme 1.1 Design of SpecimensThe test specimen matrix parameters consisting of eleven frame joint specimens are shown in Table 1. All specimens were subjected to low cycle reciprocating load. The key influencing factors included axial compression ratio nt, ratio of stirrup ρsv in joint core, and the shape of steel cruciform cross-sections (I-shaped and][-shaped) in joint core. The ratio of the volume of steel is divided by the total volume of the member. From the economic point of view, the steel content of general steel concrete column should be no more than 15%. The more commonly used steel content is 4%-8%.
| Table 1 Parameters design of the specimens |
The stirrup ratio is calculated by
| $ \rho_{\mathrm{sv}}=\frac{n_1 A_{S 1} l_1+n_2 A_{S 2} l_2}{A_{\text {cor }} \cdot s} $ | (1) |
where n1 is the number of stirrup limbs in direction b; n2 is the number of stirrup limbs in direction h; AS1 represents section area of a single stirrup; AS2 represents section area of a single stirrup; l1 is the width of stirrup in direction b; l2 is the width of stirrup in direction h; Acor is core area, and Acor=l1×l2(for frame columns); s is stirrup spacing.
The structural steel ratio is calculated as follows: The steel bones are divided into two types: I12 and 2[10 (from 2[10 spot welding of I-steel) are both hot rolled ordinary steel. The structural steel ratios are 4.47% and 6.28% corresponding to 200 mm×200 mm column section steel content. The size and geometric parameters of steel bone are shown in Fig. 1.

|
Fig.1 Size and geometric parameters of steel bone |
It is convenient to analyze the performance and shear strength of beam-column connections. The specimens were designed in such a way that the connections represent the weakest links in the assembly[16]. The beam was a rectangular section 160 mm wide and 300 mm high, and the column was a square section 200 mm wide and 200 mm high. Longitudinal reinforcement arrangement and stirrup spacing are shown in Fig. 2. The compressive strength of concrete was 110 MPa. The beam had a rectangular cross section of 160 mm width and 300 mm height, while the column had a square cross section of 200 mm width and 200 mm height. The layout of the longitudinal reinforcements and spacing of stirrup reinforcements are shown in Fig. 2. The concrete compressive strength values were derived from the test of 10 cubic samples with a side length of 150 mm[21]. All specimens adopted the same type of longitudinal reinforcement and stirrup reinforcement. The concrete cover thickness is 20 mm. All the specimens are of the same size, 1.02 m length and 1.5 m height. The mechanical parameters of material are listed in Table 2 and Table 3.

|
Fig.2 Design details of test specimens (mm) |
| Table 2 Mechanic parameters of steel bone |
| Table 3 Mechanic parameters of reinforcement |
1.2 Design of Loading Scheme
The loading device for test specimens is shown in Fig. 3. The experimental device consisted of two hydraulic jacks of 500 kN and one hydraulic jack of 3000 kN, which were applied to the beam end to simulate transverse load and constant axial load of the column respectively. The ends of the columns were hinged to constrain the top and bottom. The beams were free to move. A hydraulic jack of 2000 kN was used to apply a constant axial force on the column to simulate the weight of several layers above the column. The beam ends were subjected to cyclic reciprocating loads. The LVDT was used to measure the shear deformation of the core area of the connection. Two 200 mm displacement gauges and two 500 mm displacement gauges were used to measure the displacement and deformation of the free end and plastic hinge end of the beam respectively[22].

|
Fig.3 Loading device for test specimens |
All specimens were subjected to force-controlled loading before yielding and displacement-controlled loading in the post-yielding region. The horizontal displacement responses of Δy, 2Δy, 3Δy, 4Δy, and so on were cycled twice. It should be noted that each control point was only reloaded once before yielding. Each control point was reloaded twice to obtain the restoring force degradation curve after yielding. The load spectrum used is shown in Fig. 4[22].

|
Fig.4 Loading spectrum |
2 Fracture Morphology and Failure Mode
The first group of SRUHSC-RC-1, SRUHSC-RC-2, SRUHSC-RC-5 and SRUHSC-RC-8 specimens with nt=0.25 formed plastic hinge failure. When the lateral force reached positive 25-30 kN, the vertical bending crack within 15 cm of the beam end was observed for the first time. The crack width was about 0.02 mm. When the loading continued, vertical and oblique cracks appeared continuously at the beam end, and the crack width increased. Diagonal cracks began to appear at the core region of the connection along the direction of steel flanges under the load level of 60-75 kN. Concrete in the plastic hinge zone at beam end began to collapse at 6Δy. The strength of the specimen was controlled by the flexural capacity of beams. The bending failure of the plastic hinge was formed at the beam end.
For the specimens with larger axial pressure, the failure pattern of specimens changed. The concentrated distribution area of cracks shifted from the beam end to the node core area. For specimens SRUHC-RC-4, SRUHC-RC-6, SRUHC-RC-9 and SRUHC-RC-10, joint shear failure occurred with plastic hinge formed at the end of the beam. In the initial fracture stage, the shear deformation and stirrup strain in the core area of the joint were very small. The shear force was mainly undertaken by concrete and steel bone. As the reciprocating load continued to be applied, oblique cracks appeared in the node core, which divided the core concrete into rhombic fragments. At this time, the crack at the end of the beam was connected from top to bottom and widened, and oblique cracks appear. When the load reached 90% of the ultimate load, the main fracture in the node core area was well connected, and the crack at the beam end had little change. The stirrup strain in the node core area increased rapidly, and the shear force of the node was mainly undertaken by the section steel. The steel web began to yield, but the stirrup had not yet yielded. After the concrete in the core zone was "cracked", the concrete in the core zone could still bear most of the shear force due to the aggregate bite and friction between the oblique cracks of the concrete and the stirrup constraint.At the same time, the steel webs had yielded and entered the strengthening stage. The stirrup had gradually yielded, and the load of the joint could still increase. In the node core area, the concrete was in a state of cross-linking and the cracks were significantly widened, accompanied by a slight splitting sound. The shear deformation in the core area of the joints increased obviously and the bearing capacity reached the ultimate load value. After reaching the peak load, the concrete in the core area of the node began to be crushed and peeled off in large chunks with the increase of displacement. However, due to the existence of the section steel skeleton, the joint could still bear the load and the resistance capacity began to decline. The specimens were considered to be damaged when the bearing capacity was down to 85% of the ultimate load or the specimen lost its bearing capacity. For the specimen SRUHC-RC-3 with the axial pressure ratio 0.45 and the volume hoop ratio of the node core area 0.8%, the crack of the node core area was inhibited. However, once cracked, the cracks of the node core area developed rapidly and appeared vertically due to the increase of axial pressure. As shown in Fig. 5 that the volume ratio of the reinforcement is a key factor influencing the specimens failure pattern. For the specimen of SRUHSC-RC-11, with axial compression ratio 0.45, the shear fracture was significantly reduced and the plastic hinge was formed as a result of reinforcement volume rate increasing to 1.6% with the increase of the number of cycles of the specimens. Fig. 5

|
Fig.5 Crack pattern |
3 Results and Discussion 3.1 Hysteretic Behavior
During the experiment, load versus displacement hysteresis loops were collected to study the hysteretic behavior of SUHSRC-RC connections. The test results of eleven specimens are illustrated in Fig. 6. It can be seen that the unrecoverable residual deformation occurs during unloading and the slope of the reloading curve decreases compared with the previous cycle, resulting in stiffness degradation after the joint specimen enters the elastic-plastic deformation stage. The reason is that after the joint specimen enters the stage of elastic-plastic deformation, cracks will occur in this direction during positive loading. Due to the influence of plastic deformation, cracks in this direction cannot be completely closed after unloading. During reloading, the pressure cannot be transferred directly at the unclosed interface, which results in a significant decrease in the stiffness of the beam-column joint assembly under reverse loading. The pressure cannot be transferred directly until the crack is closed, and the stiffness can be improved. The load-displacement hysteretic curve of the specimen shows different degrees of "pinching" effect. On the one hand, with further loading to lager displacement, the concrete does not bear the tensile stress after cracking, but the tensile stress is borne by the reinforcement. Therefore, the reinforcement stress at the cracking point is the largest and the stress distribution is not uniform, leading to the bond slip between the steel and the concrete. On the other hand, the lack of built-in steel bones makes the stiffness of the members deteriorate quickly.

|
Fig.6 Hysteretic loops |
3.2 Envelope Curves
The load-displacement envelope curves of the beam ends of the three specimens with stirrup ratios of 0.8 under different axial pressure ratios are shown in Fig. 7. It can be seen that there is no significant change in the yield load and the ultimate load is slightly increased when the test axial pressure ratio increases from 0.25 to 0.38. The yield section is shortened. The bearing capacity and stiffness degradation are accelerated after reaching the ultimate load. The ultimate load decreases slightly when the test axial pressure ratio increases from 0.38 to 0.45. The degradation of bearing capacity and stiffness is accelerated significantly, which has a negative impact on the seismic resistance of the joint assembly. The envelope curves of specimens with different stirrup ratios under the same axial pressure level are shown in Figs. 7(c) and (d). It can be seen that increasing the volume of joint core area with hoop ratio can improve the bearing capacity of joint specimens for two reasons. First, increasing the hoop ratio strengthens the constraint mechanism of concrete in joint core area, thus improving the effective compressive strength of concrete at the core area of the joint. Secondly, increasing stirrup ratio directly increases the effective area of stirrup in truss mechanism. It can be seen that in Fig. 7(e), when the axial pressure ratio and volume stirrup ratio are the same but the steel ratios are different, the initial stiffness of the joint specimen is improved with the increase of steel ratio, thus improving the ultimate resistance capacity of the specimens.
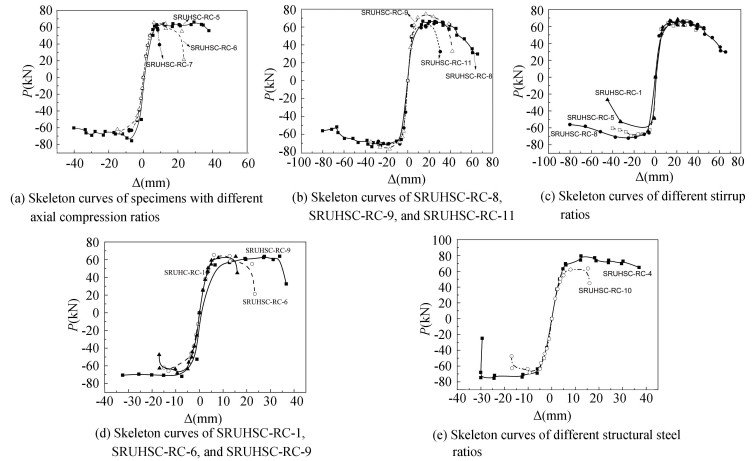
|
Fig.7 Skeleton curves of the specimens |
3.3 Ductility
The ductility coefficient of the external SRHRC-RC connections is used to quantify the inelastic deformation. According to the hysteretic response characteristics of SRUHSC-RC external nodes, the ductility coefficient μΔ is defined as[23]:
| $ \mu_{\Delta}=\frac{\Delta_y}{\Delta_u} $ | (2) |
where Δu is the limit displacement, Δy is the yield displacement. Δu is defined as the displacement of the force down to 85% Fmax[23]. For the specimens with little reinforcement and yield point, it is not difficult to determine the yield displacement (Δy) either from the reinforcement or the P-Δ load displacement curves. However, the yield displacement(Δy) is often determined from the appropriate position of curvature mutation of P-Δ curves with suitable reinforcement. For curves without obvious yield point, the general yield moment method, R. Park method and energy method can be used, as shown in Fig. 8. In this paper, the energy method is adopted to determine the equivalent yield point by using the method that the area surrounded by skeleton curve is equal. The area A1 of OAO is equal to the area A2 of ABCA and point A can be obtained, which is connected with OA and extended to intersect the ultimate load at point B and intersected with the P-Δ curve perpendicular to B at E. The corresponding displacement of point E is the yield displacement(Δy).

|
Fig.8 Schematic diagram of energy method |
The ductility coefficients of all the specimens are shown in Table 4:
| Table 4 Displacement ductility coefficient |
(1) It can be seen that the deformation capacity of the specimen with plastic hinge failure at the end of the beam is significantly better than that of the specimen with shear failure at the node core area. For example, the specimen SRUHC-RC-8 has plastic hinge failure at the beam end, μΔ=4.0, while the specimen with shear failure at the node core area and without plastic hinge at the beam end has an average displacement ductility coefficient of only 1.96(SRUHSC-RC-3 and SRUHSC-7).
(2) The displacement ductility coefficient of the member decreases significantly as the axial compression ratio increases. The reason is that the axial compression ratio is related to the ultimate compressive strain of concrete. The section strain distribution of different axial compression ratio is obviously different. The strain gradient of the cross section is larger when the axial pressure ratio is low. The strain gradient decreases with the increase of axial pressure ratio. When the axial pressure ratio is very high, the cross-section strain distribution is similar to that of axial compression members. From the theoretical analysis, it can be seen that the compression zone height is smaller when the specimens with low axial pressure are loaded to the ultimate load. The tension stirrup and section steel tensile flange have yielded, showing tensile failure. The concrete in the compression zone is small and the bearing capacity attenuation is slow. While the specimen with larger axial pressure has a larger compression zone height when it is loaded to the ultimate load, which is characterized by compression failure. The concrete in the compression zone is seriously damaged, the bearing capacity decays rapidly and the deformation capacity is poor.
(3) The joint core area stirrup ratio is also an important parameter that affects the ductility of specimens. When the volume stirrup ratio increases from 0.8% to 1.6%, the displacement ductility coefficient increases by an average of 20%.For example, the axial pressure ratios of specimens SRUHC-RC-3, SRUHC-RC-7 and SRUHC-RC-11 were all 0.45. Due to the increase of stirrup ratio, SRUHC-RC-11 still shows good ductility performance under high axial pressure. This is mainly due to the restriction effect of stirrup which restricts the development of oblique fractures in the node core area. In addition, the improvement of stirrup ratio reduces the bonding slip between steel bone and ultra-high strength concrete, ensuring the coordinated work of steel bone and concrete.
(4) The deformation capacity of specimens with higher steel rates is better than those with lower steel rates. For example, the steel rates of specimens SRUHSC-RC-1 and SRUHSC-RC-2 are 4.47% and 6.28% respectively, and the corresponding displacement ductility coefficients are 3.44 and 3.88 respectively.
3.4 Principal Strain Contrast of Steel BoneThe main tensile strains of steel web of SRUHSC-RC specimen and SRUHSC-SRC(Steel Reinforced Ultra high Strength Concrete column-Steel Reinforced Concrete beam)specimen are shown in Fig. 9. The systems of SRUHSC-RC-4 and SRUHSC-RC-5 are detailed in Table 5.

|
Fig.9 Comparison of steel strains between two different joints |
| Table 5 Control group of specimens matrix |
It has been shown that the principal tensile strain value of SRC beam specimens of steel with reinforced web is higher than the left and right RC beam specimen 1 times in the limit state. The shear ratio of the node area steel bone web of the SRC beam specimens increases because the transfer mechanism of the RC beam specimens is different from that of the SRC beam specimens[24-37]. For RC beam specimen, the pressure and tension of the beam reinforcement through the node was introduced into the surrounding concrete in the form of edge shear to core area during the period of the anchoring effect, forming shear stress field at the core area of the connections. The principal compressive stress of the shear stress field is shared by the core concrete and steel reinforced web. After the main tensile stress has caused oblique cracking of concrete in the core area of the connections, it is shared by the joint horizontal stirrup in parallel bearing direction and column longitudinal reinforcement along bearing direction. In the SRC beam specimen, the steel bone in the beam and the steel bone in the column are connected by welding, and a part of the force is directly introduced into the steel bone web in the joint area through the steel bone in the beam, resulting in the increase of the main strain of the steel bone web in the core area of the connections. Due to the plastic hinge bending failure of SRUHC-RC-4 joint, the steel web strains in the core area of the connections have not increased significantly in the later loading stage, which still restrained the concrete in the core area of the connections, as shown in Fig. 9. Moreover, the main tensile strain at the center of the web reaches the yield strain, with a greater shear bearing capacity. The steel bone strain of SRUHSC-SRC node increases greatly.
3.5 Strain Contrast of StirrupThe stirrup strain and load curves of the core area of the two joints are shown in Fig. 10. As the strength of ultra-high strength concrete increases, the elastic modulus increases and the deformation of concrete decreases, while the constraint effect of stirrup and steel bone on SRUHSC-RC joints decreases.

|
Fig.10 Comparison of stirrup strain |
As shown in Fig. 8, the stirrup strains of SRUHSRC and SRUHSC-RC joints both reach the yield strain. While the stirrup strain value of RC specimens is farless than that of SRC specimens. The reason is that beam plastic hinge failure happens on the RC specimens, while the shear fracture has not been fully developed and the stirrup tensile strength has not reached the limit strain values. The SRC specimens have sufficient elastic-plastic deformation and the stirrup tensile strength reached the limit strain values.
3.6 Displacement CompositionAs shown in Fig. 11, the beam end displacement of the RC specimens is composed of the deflection caused by shear deformation of the core area of the connection, the rotation of the plastic hinge at the beam end, and the compression deformation of the column end. The limit interlayer displacement angle of RC specimens is far less than that of SRC specimens. The ratio of the deflection at the free end to the displacement at the beam end is due to the decrease of the shear deformation in nodal zone.

|
Fig.11 Contribution of beam-column joint deformation to story drift |
4 Conclusions
The seismic performance of 11 SRUHSC-RC connections has been studied in this paper. The parameter sensitivity of SRUHSC-RC connection has been analyzed at component level. Emphasis is placed on fracture morphology, hysteretic performance, resistance capacity, ductility, energy dissipation property, strength and stiffness degradation. The main conclusions are as follows:
1) It is shown that the failure mode of the specimen does not change substantially with the increase of axial compression ratio. But the specimens show the characteristics of brittle failure as the ratio value increases. The damage of the core area of the connection is obviously reduced when the axial pressure is low, while more damage occurred in the plastic hinge region at the end of the beam. Most damage only occurred in the joint core region for the specimens when the axial pressure is high.
2) The hysteresis curves are plump and there is no evident pinching effect. It is shown that built-in steel bone can obviously improve the seismic performance of SRUHSC-RC connection.
3) nt=0.38 is the cut-off points of seismic damage evolution of SRUHSC-RC connections. When the ratio value is between 0.25 and 0.38, the peak load increases and the ultimate displacement decreases with the increase of the axial compression ratio. When the axial compression ratio is greater than 0.38, the peak load tends to be stable, the strength degradation rate increases, and the ultimate displacement decreases with the increase of the ratio value. While the value increases to 0.45, the carrying capacity decreases. An increase of the stirrup ratio and the steel ratio can contribute to the shear resistance capacity.
4) The safe use of SRUHSC-RC specimens in seismogenetic area still depends on the required ductility. Under the action of low axial compression, the specimen has good seismic performance even if less transverse reinforcement is applied. When components are subjected to high axial compression, considerable lateral reinforcement is necessary. Under high axial compression, the effect of the stirrup ratio on the deformation capacity is more significant.
| [1] |
Liu W, Jia J Q. Experimental study on the seismic behavior of steel-reinforced ultra-high-strength concreted ultra-high-strength concrete frame joints with cyclic loads. Advances in Structural Engineering, 2018, 21(2): 270-286. DOI:10.1177/1369433217717116 (  0) 0) |
| [2] |
Yao D L, Jia J Q, Wu F, et al. Shear performance of prestressed ultra high strength concrete encased steel beams. Construction and Building Materials, 2014, 52: 194-201. DOI:10.1016/j.conbuildmat.2013.11.006 (  0) 0) |
| [3] |
Pu X C, Wang Z J, Wang C, et al. Mechanical properties of super high-strength and high performance concrete. Journal of Building Structures, 2002, 23(6): 49-55. DOI:10.14006/j.jzjgxb.2002.06.007 (  0) 0) |
| [4] |
Hanson N W, Connor H W. Seismic resistance of reinforced concrete beam-column joints. Journal of the Structural Division, 1967, 93(5): 533-559. DOI:10.1061/JSDEAG.0001785 (  0) 0) |
| [5] |
Paulay T, Park R, Priestley M J N. Reinforced concrete beam-column joints under seismic actions. Journal of the American Concrete Institute, 1978, 75(11): 585-593. DOI:10.14359/10971 (  0) 0) |
| [6] |
Taylor C W, Montoya K F, Jáuregui D V, et al. Feasibility analysis of using UHPC in prestressed bridge girders. Proceedings of the 2011 Structures Congress. Nevada: ASCE, 2011, 203-214. (  0) 0) |
| [7] |
Tao M X, Fan J S, Nie J G. Seismic behavior of steel reinforced concrete column-steel truss beam hybrid joints. Engineering Structures, 2013, 56(3): 1557-1569. DOI:10.1016/j.engstruct.2013.07.029 (  0) 0) |
| [8] |
Hakuto S, Park R, Tanaka H, et al. Seismic load tests on interior and exterior beam-column joints with substandard reinforcing details. Structural Journal, 2000, 97(1): 11-25. DOI:10.14359/829 (  0) 0) |
| [9] |
Bonacci J, Pantazopoulou S. Parametric investigation of joint mechanics. ACI Structural Journal, 1993, 90(1): 61-71. DOI:10.14359/4211 (  0) 0) |
| [10] |
Kamimura T, Takeda S, Tochio M. Influence of joint reinforcement on strength and deformation of interior beam-column subassemblages Proceedings of the 12th World Conference on Earthquake Engineering. Auckland, New Zealand: WCEE, 2000, 2267. (  0) 0) |
| [11] |
Shin M, LaFave J M. Modeling of cyclic joint shear deformation contributions in RC beam-column connections to overall frame behavior. Structural Engineering and Mechanics, 2004, 18(5): 645-669. DOI:10.12989/sem.2004.18.5.645 (  0) 0) |
| [12] |
Lin C M, Restrepo J I. Seismic behavior and design of reinforced concrete interior beam-column joints. Bulletin of the New Zealand Society for Earthquake Engineering, 2002, 35(2): 108-128. DOI:10.5459/bnzsee.35.2.108-128 (  0) 0) |
| [13] |
Cheng C T, Chen C C. Seismic behavior of steel beam and reinforced concrete column connections. Journal of Constructional Steel Research, 2004, 61(5): 587-606. DOI:10.1016/j.jcsr.2004.09.003 (  0) 0) |
| [14] |
Kim J, LaFave J M. Key influence parameters for the joint shear behavior of reinforced concrete(RC) beam-column connections. Engineering Structures, 2007, 29: 2523-2539. DOI:10.1016/j.engstruct.2006.12.012 (  0) 0) |
| [15] |
Parra-Montesinos G, Wight J K. Seismic response of exterior RC column-to-steel beam connections. Journal of Structure Engineering, 2000, 126(10): 1113-1121. DOI:10.1061/(ASCE)0733-9445(2000)126:10(1113) (  0) 0) |
| [16] |
Sheikh T M, Deierlein G G, Yura J A, et al. Beam-column moment connections for composite frames: Part 1. Journal of Structural Engineering, 1989, 115(11): 2858-2876. DOI:10.1061/(asce)0733-9445 (  0) 0) |
| [17] |
Parra-Momtesinos G, Wight J K. Modeling shear behavior of hybrid RCS beam-column connections. Journal of Structural Engineering, 2001, 127(1): 3-11. DOI:10.1061/(ASCE)0733-9445(2001)127:1(3) (  0) 0) |
| [18] |
Chen C C, Suswanto B, Lin Y J. Behavior and strength of steel reinforced concrete beam-column joints with single-side force inputs. Journal of Constructional Steel Research, 2009, 65(8-9): 1569-1581. DOI:10.1016/j.jcsr.2009.04.003 (  0) 0) |
| [19] |
Bugeja M N, Bracci J M, Moore W P. Seismic behavior of composite RCS frame systems. Journal of Structural Engineering, 2000, 126(4): 429-436. DOI:10.1061/(ASCE)0733-9445(2000)126:4(429) (  0) 0) |
| [20] |
Boulekbache B, Hamrat M, Chemrouk M, et al. Influence of yield stress and compressive strength on direct shear behaviour of steel fibre-reinforced concrete. Construction and Building Materials, 2012, 27(1): 6-14. DOI: CABM(2012)27:1<p.6:IOYSAC>2.0.TX;2-W.
(  0) 0) |
| [21] |
General Administration of Quality Supervision, Inspection and Quarantine, Ministry of Construction of the People's Republic of China. GB50107-2010, Standard for Test and Evaluation of Concrete Compression Strength. Beijing: General Administration of Quality Supervision, 2010.
(  0) 0) |
| [22] |
Ministry of Construction of the People's Republic of China. JGJ101-96, Specificating of Test Methods for Earthquake Resistant Building. Beijing: Ministry of Construction of the People's Republic of China, 1997.
(  0) 0) |
| [23] |
Liu W, Jia J Q. Experimental studies on seismic behavior of exterior SRUHSC joints. Journal of Harbin Institute of Technology(New Series), 2017, 24(5): 61-70. DOI:10.11916/j.issn.1005-9113.16120 (  0) 0) |
| [24] |
Zhang L X, Hsu T T C. Behavior and analysis of 100Mpa concrete membrane elements. Journal of Structural Engineering, 1998, 124(1): 24-34. DOI:10.1061/(ASCE)0733-9445(1998)124:1(24) (  0) 0) |
| [25] |
Wang H T, Wang L C. Experimental study on static and dynamic mechanical properties of steel fiber reinforced lightweight aggregate concrete. Construction and Building Materials, 2013, 38(2): 1146-1151. DOI:10.1016/j.conbuildmat.2012.09.016 (  0) 0) |
| [26] |
Wang T C, Chen H C, Guo Y L, et al. Rigidity degeneration of RC column under two-way horizontal cyclic loads. Journal of Tianjin University (Science and Technology), 2005, 38(12): 1058-1062. (  0) 0) |
| [27] |
Yan C W, Jia J Q, Zhang J. Seismic behavior of steel reinforced ultra high strength concrete column and reinforced concrete beam connection. Transactions of Tianjin University, 2010, 16: 309-316. DOI:10.1007/s12209-010-1344-z (  0) 0) |
| [28] |
Fan G X, Song Y P, Wang L C. Experimental study on the seismic behavior of reinforced concrete beam-column joints under various strain rates. Journal of Reinforced Plastics and Composites, 2014, 33(7): 601-618. DOI:10.1177/0731684413512706 (  0) 0) |
| [29] |
Park S, Mosalam K. Analytical model for predicting shear strength of unreinforced exterior beam-column joints. ACI Structural Journal, 2012, 109(14): 149-160. DOI:10.14359/51683626 (  0) 0) |
| [30] |
Chen C C, Lin K T. Behavior and strength of steel reinforced concrete beam-column joints with two-side force inputs. Journal of Constructional Steel Research, 2009, 65(3): 641-649. DOI:10.1016/j.jcsr.2008.03.010 (  0) 0) |
| [31] |
Parra-Montesinos G J, Liang X, Wight J K. Towards deformation-based capacity design of RCS beam-column connection. Journal of Engineering Structures, 2003, 25(5): 681-690. DOI:10.1016/S0141-0296(02)00177-3 (  0) 0) |
| [32] |
Kim K, Noguchi H. A study on the ultimate shear strength of connections with RC columns and steel beams. Journal of Structural and Construction Engineering, 1998, 507: 163-169. DOI:10.3130/aijs.63.163_2 (  0) 0) |
| [33] |
Sakaguchi N. Shear capacity of beam-column connection between steel beams and reinforced concrete columns. Transactions of AIJ, 1991, 428: 69-77. DOI:10.3130/aijsx.428.0_69 (  0) 0) |
| [34] |
Tang J R, Chen X H. Behavior and calculation of shear capacity of steel reinforced concrete beam-column joint. Journal of Building Structure, 1990, 11(4): 28-36. (  0) 0) |
| [35] |
Vecchio F J, Collins M P. Compression response of cracked reinforced concrete. Journal of Structural Engineering, 1993, 119(12): 3590-3610. DOI:10.1061/(ASCE)0733-9445(1993)119:12(3590) (  0) 0) |
| [36] |
Li B, Pan T C, Than C T. Effects of axial compression load and eccentricity on seismic behavior of nonseismically detailed interior beam-wide column joints. Journal of Structural Engineering, 2009, 135(7): 774-784. DOI:10.1061/(ASCE)0733-9445(2009)135:7(774) (  0) 0) |
| [37] |
Frederic L, Paultre P. Behavior of high-strength concrete columns under cyclic flexure and constant axial load. Structural Journal, 2000, 97(4): 591-601. (  0) 0) |
 2023, Vol. 30
2023, Vol. 30



 6
6 14
14 6
6