2. School of Aeronautics and Astronautics, University of Electronic Science and Technology of China, Chengdu 611731, China;
3. School of Mechanical and Electrical Engineering, Wenzhou University, Wenzhou 325035, Zhejiang, China
In the past several decades, production and machine maintenance planning have been a hot topic for many engineers and researchers. Mostly, they are separately optimized. Since they both have impacts on the machine's capacity and reliability, there is an increasing interest in developing optimization models that integrate maintenance planning and production scheduling jointly in recent years, especially. In the related literatures, they are generally divided into three categories.
Some research focuses on production planning with given deterministic machine unavailability constraints. In these studies, preventive maintenance activities were considered as machine unavailability periods to optimize production performance measures under the deterministic machine unavailability constraints, and scheduling rules and algorithms were developed to solve these problems. Lee et al.[1] presented reviews of local search methods and machine scheduling with unavailability constraints. Sanlaville and Schmidt[2] proved the problems are NP-hard. Kubzin and Strusevich[3] considered tow-machine open shop and completion time of all activities to be scheduled. Ma et al.[4] provided detailed and comprehensive reviews on all kinds of deterministic scheduling problems with unavailability constraints.
Some research focuses on flexible unavailability constraints. In this category, preventive maintenance needs to be scheduled. Qi[5], Yang[6] and Lee[7] considered a single machine scheduling and maintenance simultaneously to minimize the total completion time. Lee and Chen[8] extended this integrated problem for parallel systems to reduce completion time. Chen[9] studied both integrated single and parallel machine arrange problems and took total delay as a performance measure. Chen[10] also studied the same problem with the assumption of nonresumable jobs to minimize the makespan. Sbihi and Varnier[11] and Mosheiov and Sarig[12] proposed continuous working time. Levin[13] considered two parallel identical machines and assumed that two machines must be maintained simultaneously. Chen[14] considered a single machine system planning problem to minimize the number of tardy jobs while Batun[15] aimed to establish the model by minimizing total flow time. Sun[16] proposed two integrated models on two identical parallel machines with the objective of minimizing makespan and whole accomplishment time of jobs, respectively. Low et al.[17] assumed that pre-emptive operation was not allowed and proposed some heuristic algorithms to the single machine problems with respect to final minimization of makespan. Yang et al.[18] investigated a single machine scheduling problem with both resumable and nonresumable cases, in terms of total completion time.
Other research studies the combination of production arrangement and preventive maintenance with stochastic failures. They consider that scheduling may be affected by unexpected machine breakdowns with stochastic features and corrective maintenance is carried out. Lee[19] studied scheduling problems involving maintenance and repair. Cassady and Kutanoglu[20] investigated a single scheduling model integrating production scheduling and preventive maintenance. Chen and Liao[21] considered maintenance scheduling problems with five specific maintenance situations in terms of the number of tardy jobs. Sortrakul [22] developed heuristics based on genetic algorithm (GA) flexibly to solve the integrated optimization model. Jin et al.[23] studied the integrated optimization model with multiple objectives, and multi-objective genetic algorithms were developed. Pan et al.[24] considered a variable maintenance time. Later, Pan et al.[25] studied a single machine scheduling model that integrates the two models. Wang and Liu[26] extended the model proposed by Cassady[27] and developed a branch and bound algorithm.
However, most of the above literatures aimed to optimize the production performance. In reality, many industries have arrangements between production department (PD) and maintenance department (MD). Indeed, competition exists between PD and MD on account of KPI, and both of them are committed to better performance. Therefore, scheduling by optimization method may not meet their needs.
In this paper, an integrated optimization model of maintenance planning and production scheduling is proposed for a single machine system with stochastic failures. First, game theory is introduced to solve the integrated scheduling problem with the aim of making performance of both of them as better as possible. The performance measure for production is to minimize the whole earliness or tardiness cost, while MD aims to minimize the total maintenance cost. In this model, imperfect preventive maintenance is considered and backwards induction methods are applied to cope with the problem. The method proposed in the paper can reduce the total maintenance costs from a company perspective. The optimized schedule would balance PD and MD to improve the overall efficiency.
The rest of the paper is organized as follows: Section 1 states the problem and two game-theory based models. In Section 2, the proposed backwards induction method is presented. Section 3 compares the performance of the proposed two game-theory models with other two optimization models by computational tests. Section 4 concludes the paper and provides directions on future research.
1 Model Description 1.1 Problem DescriptionA set of jobs J={J1, J2, …, Jn} with deterministic processing time pj and due date dj(j=1, 2, ..., n) is to be scheduled on a single machine. All jobs are available at the beginning of the time horizon. The machines are subject to Weibull probability distribution, where λ(t) represents the failure rate function of the machine with shape parameter β and scale parameter η. It is assumed that preventive maintenance is imperfect. When an unexpected failure happens, minimal repairs are adopted to get the machine back up and running without changing the failure rate. It is assumed that the time duration of minimal repair is negligible compared with the processing time. Meanwhile, the works are preventive for PM and can be resumed with repair. The classic control limit policy is adopted for PM, which indicates that PM is carried out whenever the reliability of the machine reaches the predetermined threshold.
The integrated model intends to apply scheduling rules and dynamic game theory with perfect information to decide the ideal work sequence and the ideal PM threshold. Two players are PD and MD. PD aims to minimize whole expected advance or delay costs, while MD points at minimizing the total expected maintenance costs. The game model seeks to obtain best job sequence and PM threshold to balance the profits of two players.
In the following, expressions of the total expected maintenance costs and the total advance or delay costs are derived. Fig. 1 shows an illustration of problem in Gantt chart, where Bi is the ith batch of jobs, PMi is the ith maintenance activity, l is the number of batches.

|
Fig.1 Illustration of the problem under consideration |
1.2 Total
Expected Maintenance Cost
Let R be the optimal PM reliability threshold, and λ1(t) be the initial failure rate function. Then the initial reliability function is as follows:
| $ R_{1}(t)=\exp \left[-\int_{0}^{t} \lambda(t) \mathrm{d} t\right]=\mathrm{e}^{-\left(\frac{t}{\eta}\right) \beta} $ |
and the initial PM cycle is:
| $ R_{1}\left(\tau_{1}^{\prime}\right)=R=\mathrm{e}^{-\left(\frac{\tau_{1}^{\prime}}{\eta}\right) \beta} $ | (1) |
| $ \tau_{1}^{\prime}=(-\ln R)^{1 / \beta} \eta $ | (2) |
Because the initial age of the machine is a0, the initial PM cycle is adjusted as follows:
| $ \tau_{1}=\tau_{1}^{\prime}-a_{0} $ | (3) |
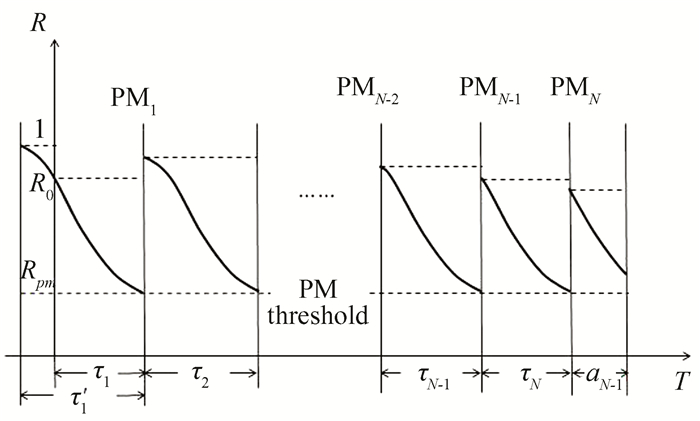
Since PM is imperfect, PM cycle is reduced with the increase of the age of the machine. Let a denote degradation rate, 0 < a < 1. Fig. 2 shows variation curves of reliability of the machine, where R0 is the initial reliability, aN+1 is the remaining production task after the last PM. The failure rate distribution function after the ith PM is:
| $ \lambda_{(i+1)}(t)=\lambda_{1}\left(t+i a \tau_{1}^{\prime}\right) $ | (4) |
|
Fig.2 Variation curves of reliability |
The reliability function after the ith PM is:
| $ \begin{aligned} & R_{(i+1)}(t)=\exp \left[-\int_{0}^{t} \lambda_{(i+1)}(t) \mathrm{d} t\right]= \\ & \quad \exp \left[-\int_{0}^{t} \lambda_{1}\left(t+i a \tau_{1}^{\prime}\right) \mathrm{d} t\right]=\mathrm{e}^{-\left(\frac{t+i a \tau_{1}^{\prime}}{\eta}\right) \beta} \end{aligned} $ | (5) |
According to Eq.(5), PM cycle after the ith PM is:
| $ R_{(i+1)}\left(\tau_{(i+1)}\right)=R=\mathrm{e}^{-\left(\frac{\tau_{(i+1)+i a \tau_{1}^{\prime}}}{\eta}\right) \beta} $ | (6) |
| $ \tau_{(i+1)}=(1-i a) \tau_{1}^{\prime} $ | (7) |
The total number of PM during the time horizon can be solved by the following equation:
| $ \text { MS }=\sum\limits_{i=1}^{N} \tau_{i}=\left(N-\frac{N(N-1)}{2} a\right) \tau_{1}^{\prime} $ | (8) |
where MS
| $ \frac{a}{2} N^{2}-\left(\frac{a}{2}+1\right) N+\frac{\mathrm{MS}}{\tau_{1}^{\prime}}=0 $ | (9) |
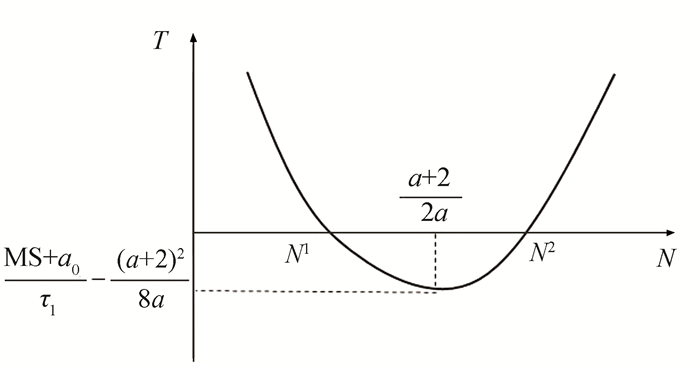
There are two solutions N1 and N2, N1 < N2, Lemma 1 is proposed to prove that the smaller one N1 is the feasible solution.
Lemma 1 Eq.(9) has the unique feasible solution, which is the smaller one of the two solutions.
Proof Put N into Eq.(7):
| $ \tau_{N}=(1-(N-1) a) \tau_{1}^{\prime}>0 \Rightarrow 1-(N-1) a>0 $ | (10) |
The coordinate of the lowest point of formula (9) is ((a+2)/2a, MS/τ1-(a+2)2/8a), as shown in Fig. 3. According to Fig. 3, N1≤(a+2)/2a, N2>(a+2)/2a. Put the maximal value of N1=(a+2)/2a and the minimum value of N2=(a+2)/2a+1 into formula (10), there is:
| $ \left\{\begin{array}{l} 1-\left(N^{1}-1\right) a=1-\left(\frac{a+2}{2 a}-1\right) a=\frac{a}{2}>0 \\ 1-\left(N^{2}-1\right) a=1-\left(\frac{a+2}{2 a}+1-1\right) a=-\frac{a}{2}<0 \end{array}\right. $ | (11) |
|
Fig.3 Illustration of Eq.(9) |
Comparing Eq.(10) and Eq.(11), it can be concluded that N2 is not feasible because it does not satisfy the inequality while N1 is feasible. So, the equation only has a unique feasible solution, and it is the smaller one.
After the Nth PM, the remaining product task aN+1 is:
| $ a_{N+1}=\mathrm{MS}-\sum\limits_{i=1}^{N} \tau_{i} $ | (12) |
The total maintenance costs consist of PM costs and minimal repair costs are:
| $ M_{c}(R)=N c_{p}+c_{r}\left(\sum\limits_{i=1}^{N} m\left(\tau_{i}\right)+m\left(a_{N+1}\right)\right) $ | (13) |
where cp and cr represent PM cost and minimal repair cost respectively. m(τi) represents the expected failures during the ith PM cycle:
| $ \begin{gathered} m\left(\tau_{i}\right)=m\left((1-(i-1) a) \tau_{1}^{\prime}\right)= \\ \int_{0}^{(1-(i-1) a) \tau_{1}^{\prime}} \lambda_{1}(t) \mathrm{d} t= \\ \int_{0}^{(1-(i-1) a) \tau_{1}^{\prime}} \frac{\beta}{\eta}\left(\frac{t}{\eta}\right)^{\beta-1} \mathrm{~d} t= \\ \left(\frac{(1-(i-1) a) \tau_{1}^{\prime}}{\eta}\right)^{\beta}=\left(\frac{\tau_{i}}{\eta}\right)^{\beta} m(\tau) \end{gathered} $ | (14) |
Total earliness/tardiness costs consist of total earliness costs and tardiness costs.
In a single machine system, it is assumed that:
| $ x_{[i] j}=\left\{\begin{array}{l} 1, J_{j} \text { is the } i \text { th job in order } \\ 0, \text { otherwise } \end{array}\right. $ | (15) |
Then the equations must be satisfied:
| $ \sum\limits_{i=1}^{n} x_{[i] j}=1, j=1, \ldots, n $ | (16) |
| $ \sum\limits_{j=1}^{n} x_{[i] j}=1, i=1, \ldots, n $ | (17) |
Let p[i] be the processing time of the ith job in the sequence, d[i]be the due date time of the ith job in the sequence, then there is:
| $ p_{[i]}=\sum\limits_{j=1}^{n} p_{j} x_{[i] j} $ | (18) |
| $ d_{[i]}=\sum\limits_{j=1}^{n} d_{j} x_{[i] j} $ | (19) |
The number of PM from time zero to the end of the ith job in the sequence can be solved by the following equation:
| $ A_{[i]}=\sum\limits_{i=1}^{N_{[i]}} \tau_{i}=\left(N_{[i]}-\frac{N_{[i]}\left(N_{[i]}-1\right)}{2} a\right) \tau_{1}^{\prime} $ | (20) |
where
| $ C_{[i]}=A_{[i]}+N_{[i]} t_{p} $ | (21) |
where tp denotes time length of PM. The total earliness/tardiness costs are:
| $ \begin{gathered} \operatorname{ET}_{c}(R)=\sum\limits_{i=1}^{n}\left(\mu_{\text {max }}\left(d_{[i]}-C_{[i]}, 0\right)+\right. \\ \left.\varphi_{\text {max }}\left(C_{[i]}-d_{[i]}, 0\right)\right) \end{gathered} $ | (22) |
where μ and φ represent the unit earliness penalty and the unit tardiness penalty respectively.
1.4 Game ModelsFor MD, they focus on the preventive maintenance policy. The maintenance model can be obtained from the analysis above:
| $ \min M_{c}(R) $ | (23) |
| $ \text { s.t. }\ \ \ \ 0<R<1 $ | (24) |
For PD, production scheduling needs to be considered first. The production scheduling model is given:
| $ \operatorname{minET}_{c}(R) $ | (25) |
| $ \text { s.t. } \quad 0<R<1 $ | (26) |
| $ \sum\limits_{i=1}^{n} x_{[i] j}=1, j=1, \ldots, n $ | (27) |
| $ \sum\limits_{j=1}^{n} x_{[i] j}=1, i=1, \ldots, n $ | (28) |
| $ p_{[i]}=\sum\limits_{j=1}^{n} p_{j} x_{[i] j} $ | (29) |
| $ d_{[i]}=\sum\limits_{j=1}^{n} d_{j} x_{[i] j} $ | (30) |
| $ x_{[i] j} \in\{0, 1\}, i=1, \ldots, n, j=1, \ldots, n $ | (31) |
To balance the two departments and reduce the total costs, the dynamic game theory is applied to decide the ideal work sequence and the ideal PM threshold. Two players are PD and MD. The game model is a three-stage dynamic model based on alternating-offers game. It consists of two players with an infinite-horizon game. One player is the proposer. The proposer requires the PM threshold. The other player is the responder, who observes the proposer's demand and decides either to accept or reject it. In the first stage, Player 1 is the proposer and Player 2 is the responder. In the next stage, the roles are reversed. If the responder rejects the proposal, the profits of the two players will decrease by δ(0 < δ < 1). Suppose that there are only three-stage. In the third stage, the responder must accept the proposal and the game ends. Two game models are developed. In Model 1, MD serves as the proposer first. In Model 2, PD proposes first.
1) Model 1
Participants: MD, PD.
Game order:
(1) MD proposes a PM threshold R1.
(1*) PD determines whether to reject or accept the proposal.
(2) If PD accepts the proposal, the game is over. Otherwise, PD proposes another PM threshold R2.
(2*) MD determines whether to reject or accept the proposal.
(3) If MD accepts the proposal, the game is over; otherwise, MD proposes the final PM threshold R, PD must accept it, and the game is over.
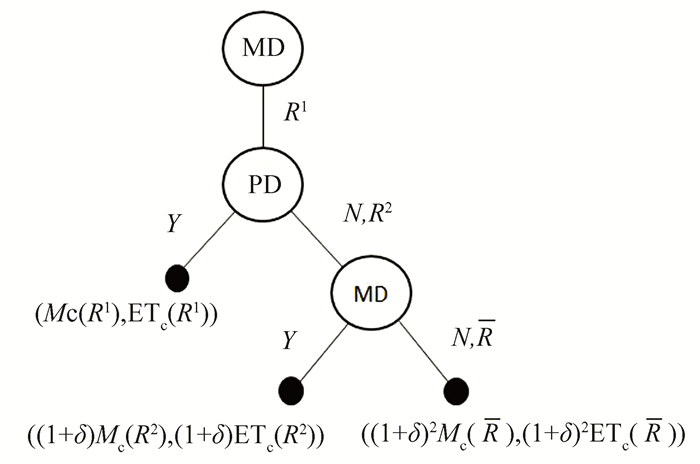
Fig. 4 reveals the extension of Model 1, where Y means 'accept' and N means 'reject'.
|
Fig.4 Extension of Model 1 |
2) Model 2
Participants: MD, PD.
Game order:
(1) PD proposes a PM threshold R1.
(1*) MD determines whether to reject or accept the proposal.
(2) If MD accepts the proposal, the game is over; otherwise, MD proposes another PM threshold R2.
(2*) PD determines whether to reject or accept the proposal.
(3) If PD accepts the proposal, the game is over; otherwise, PD proposes the final PM threshold R, MD must accept it, the game is over.
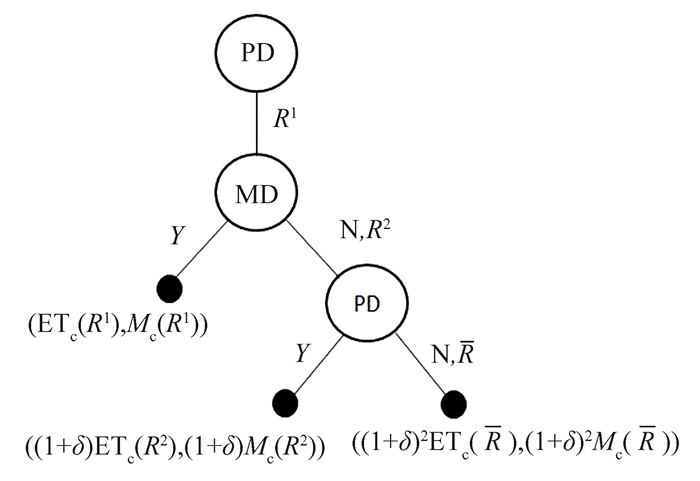
Fig. 5 reveals the extension of Model 2, where Y means 'accept' and N means 'reject'.
|
Fig.5 Extension of Model 2 |
2 Solution Method 2.1 Solution to Model 1
Solution to Model 1 is to find the PM threshold that is the subgame perfect Nash equilibrium, and here is the following lemma.
Lemma 2 The subgame perfect Nash equilibrium of Model 1 is a function of R and δ.
Proof Backward induction is used.
When the game continues to the third stage, total maintenance cost is (1+δ)2Mc(R), total production cost is (1+δ)2ETc(R).
In the second stage, the proposer is PD. If MD rejects the proposal, in the third stage, whatever R that the MD proposes, PD has to accept it. At that time, PD is in a disadvantage situation. If PD has already rejected the proposal of the first stage, it has to propose a R2, whether MD accepts or rejects this proposal. There is no difference between the value of the costs. MD would accept the proposal. At the same time, the costs of PD at this stage are smaller than the third stage. This kind of proposal satisfies PD since it best meets PD's profits. R2 can be calculated as follows :
| $ (1+\delta) M_{c}\left(R^{2}\right)=(1+\delta)^{2} M_{c}(\bar{R}) $ | (32) |
| $ (1+\delta) \operatorname{ET}_{c}\left(R^{2}\right)<(1+\delta)^{2} \operatorname{ET}_{c}(\bar{R}) $ | (33) |
Based on this, we move back to the first stage. The proposer is MD. If PD rejects the proposal, PD can acquire the largest profits in the second stage. So MD has to propose a R1, whether PD accepts or rejects this proposal, it has no difference between the value of the costs, then PD would accept the proposal, at the same time, the costs of MD at this stage is smaller than the second stage. This kind of proposal satisfies MD since it best meets MD's profits. R1 can be calculated by the following equation:
| $ \operatorname{ET}_{c}\left(R^{1}\right)=(1+\delta) \operatorname{ET}_{c}\left(R^{2}\right) $ | (34) |
| $ M_{c}\left(R^{1}\right)<(1+\delta) M_{c}\left(R^{2}\right) $ | (35) |
R1 solved by the previous equation can both make MD and PD get the largest profits, so this is the subgame perfect Nash equilibrium of Model 1. Based on Eqs. (21) and (22), it can be concluded R2 is a function of R and δ:
| $ R^{2}=g(\bar{R}, \delta) $ | (36) |
According to Eqs.(23) and (24), R1 is a function of R2 and δ:
| $ R^{1}=f\left(R^{2}, \delta\right) $ | (37) |
Based on Eqs.(25) and (26), R1 is a function of R and δ:
| $ R^{1}=f(g(\bar{R}, \delta), \delta) $ | (38) |
So it proves that R1 is the subgame perfect Nash equilibrium of Model 1.
2.2 Solution to Model 2The solving process of Model 2 is similar to that of Model 1. According to Lemma 2, the subgame perfect Nash equilibrium of Model 2 is a function of R and δ. With the adoption of the backward deduction method, in the second stage, R2 satisfies the following equations:
| $ (1+\delta) \operatorname{ET}_{c}\left(R^{2}\right)=(1+\delta)^{2} \operatorname{ET}_{c}(\bar{R}) $ | (39) |
| $ (1+\delta) M_{c}\left(R^{2}\right)<(1+\delta)^{2} M_{c}(\bar{R}) $ | (40) |
In the first stage, Rs1satisfied the following equations:
| $ M_{c}\left(R^{1}\right) =(1+\delta) M_{c}\left(R^{2}\right) $ | (41) |
| $ \operatorname{ET}_{c}\left(R^{1}\right) <(1+\delta) \operatorname{ET}_{c}\left(R^{2}\right) $ | (42) |
R1 solved by the previous equation is the subgame perfect Nash equilibrium of Model 2. Like Eqs.(25)-(27), it can be concluded that R1 is a function of R and δ.
3 Computational ExperimentsThe results of the game model are shown in the section. It is compared with two optimization models. The procedures are programmed in Matlab 2013b and run on PC with an Intel 2.10 GHz CPU and 4.00GB RAM.
3.1 Experimental DesignThe test procedure applied in this paper is similar to that in Ref.[26]. Three parameters are set: n, η, β (i.e., n=10, η=100, β=3), and the only focus is the impacts of different tp on two models. There are more parameters cp=5000, cr=15000, μ=100, φ=200, a=0.01.Each experiment consists of a certain number of randomly generated problems:
(1) The initial age of single machine a0 is integer within the range from 1 to 100 with a discrete uniform random distribution.
(2) The job processing time is integer within the range from 1 to 100 with a discrete uniform random distribution.
(3) The due date of a job is integer within the range from (1-C-E/2)·MS to (1-C+E/2)·MS, where C=0.2, E=0.6.
(4) The time length of PM tp={5, 50, 120}.
Three rules are set for the sequence of jobs:
(1) SPT: jobs are sorted in increasing order of processing time.
(2) LPT: jobs are sorted in decreasing order of processing time.
(3) EDD: jobs are sorted in increasing order of due date time.
According to Lemma 2, the subgame perfect Nash equilibrium of two models is a function of R and δ, R and δ are taken as equal to 0.1, 0.2, …, 0.9.
The three rules are applied for sorting the jobs and the two models are applied for optimizing the scheduling. The experimental results are based on 6 methods after combination.
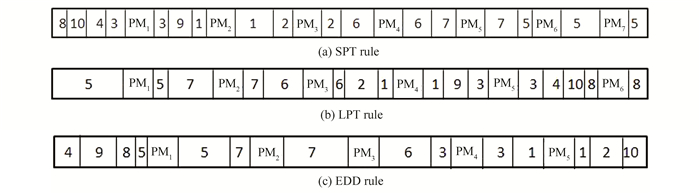
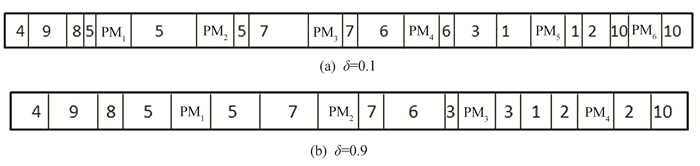
3.2 Performance of Game ModelsIn this section, tp=50, R=0.5, and three rules on Model 1 and Model 2 with different δ are tested. The performances are presented in Tables 1-6, where CTotal(R) is the total costs, CTotal(R)=ETc(R)+Mc(R).Fig. 6 shows schedule of Model 1 of three rules under δ=0.1, and Fig. 7 shows schedule of Model 2 of EDD rule under δ=0.1 and δ=0.9.
| Table 1 Costs associated with SPT rule of Model 1 |
| Table 2 Costs associated with LPT rule of Model 1 |
| Table 3 Costs associated with EDD rule of Model 1 |
| Table 4 Costs associated with SPT rule of Model 2 |
| Table 5 Costs associated with LPT rule of Model 2 |
| Table 6 Costs associated with EDD rule of Model 2 |
|
Fig.6 Schedule of Model 1of δ=0.1 |
|
Fig.7 Schedule of Model 2 of EDD rule |
According to the obtained results, it can be concluded that:
(1) Under the same rule, for Model 1, R, ETc(R) and CTotal(R) increase with the increase of δ while Mc(R) decreases except for one rule (SPT); for Model 2, R decreases with the increase of δ while Mc(R) increases, and ETc(R) decreases except for one rule(SPT);
(2) If δ is fixed, for Model 1, it is always better to sort jobs on increasing order of due date time for minimizing R, ETc(R) and CTotal(R); in 60% of the cases, the minimum value of Mc(R) is obtained under SPT rule; for Model 2, for minimizing Mc(R), it is always better to sort jobs on SPT rule except for δ=0.1, 0.2, 0.3; for minimizing ETc(R) and CTotal(R), it is always better to sort jobs on EDD rule.
(3) Under the same rule, if δ is fixed, PM threshold and the value of ETc(R) of Model 1 are always bigger than that of Model 2 while the value of Mc(R) is smaller. It can be concluded that in game models, the player who serves as the proposer first has advantage of acquiring more profits.
From Fig. 6, if δ=0.1, under SPT rule, the number of PM is 7, which is more than the number of the other two rules, which means the completion time of all jobs is the longest. The number of PM is 5 under EDD rule. To make further observation, the EDD rule is fixed, Fig. 7(a) is the sequence of Model 2 of δ=0.1, and Fig. 7(b) is the sequence of Model 2 of δ=0.9. It can be concluded that when δ gets larger, the number of PM is fewer, and the completion time of all jobs is shorter.
3.3 Comparison with Two Optimization ModelsIn this section, the proposed game models are compared with other two optimization models. The objective of optimization Model 1(OM1) is to minimize the total costs (including earliness/tardiness penalty costs and maintenance costs), which can be stated as follows:
| $ \operatorname{Min} C_{\text {Total }}(R)=\operatorname{ET}_{c}(R)+M_{c}(R) $ | (43) |
| $ \text { s.t. } \quad \sum\limits_{i=1}^{n} x_{[i] j}=1, i=1, 2, \cdots, n $ | (44) |
| $ \sum\limits_{j=1}^{n} x_{[i] j}=1, j=1, 2, \cdots, n $ | (45) |
| $ x_{[i] j}=0 \text { or } 1, i=1, 2, \cdots, n ; j=1, 2, \cdots, n $ | (46) |
This model can be solved by Monto-Carlo method.
Optimization Model 2 (OM2) is the conventional independent decision model. It is applies EDD rule to sort the jobs, and the optimal PM cycle is calculated by minimizing the average cost rate. Let Ti be the ith PM cycle, the average maintenance cost of ith PM cycle is:
| $ C_{i}=\frac{c_{p}+c_{r} \int_{0}^{\tau} \lambda_{i}(t) \mathrm{d} t}{t_{p}+T_{i}} $ | (47) |
It can be solved by the following equation:
| $ \left.\frac{\mathrm{d} C_{i}}{\mathrm{~d} T_{i}}\right|_{T}=0 $ | (48) |
According to the optimal PM cycle and EDD rule, the total costs can be calculated.
Under the same rule (EDD rule), δ=0.1. Compare the PM threshold and total costs of three methods with different R and tp. The perfomances are presented in Tables 7 and 8.
| Table 7 Comparison between Model 1 and two optimization methods |
| Table 8 Comparison between Model 2 and two optimization methods |
From Tables 7 and 8, it can be concluded that:
(1) Compare game models with OM1. When tp=50, R=0.2, the value of total costs of Model 2 is the same as the value of OM1. In fact, there is at least one combination of δ and R, making the total costs of game models equal to that of OM1 for the same tp. For example, when tp=50, R=0.1, δ=0.3, the costs of Model 1 are the same as those of OM1. When tp=5, OM1 has better performance. With the increase of tp, PM threshold becomes smaller which is not consistent with the actual situation in the factory, but game models have more combinations to choose.
(2) Compare game models with OM2. When tp=5, it is better to choose OM2. With the increase of tp, when tp=50, the result of OM2 is 2.5 times larger than that of Model 1, the same as Model 2. When tp=120, the result of OM2 is nearly 5 times larger than that of Model 1, and over 5 times larger than the maximum value of Model 2. Thus, it can be concluded that, when tp increases, game models perform better.
4 ConclusionsThis paper proposes a new integrated model of PM planning and production scheduling for a single machine system based on game theory. The aim is to minimize the costs of the PD and MD, respectively. Three-stage dynamic game with perfect information was applied to establish and solve the models, and were compared with other two optimization models. Results show that the player who proposes first has advantage over profits, and when the time duration of PM action gets longer, the game models perform better. This method can coordinate MD and PD better. The model integrating PM planning and production scheduling would benefit the company by decreasing the total costs.
The proposed models are suitable for preemptive jobs. In future work, the aim is to develop game models for non-preemptive jobs. In addition, we are interested in developing integrated game models for multi-machine systems.
| [1] |
Lee C-Y, Lei L, Pinedo M. Current trends in deterministic scheduling. Annals of Operations Research, 1997, 70: 1-41. DOI:10.1023/A:1018909801944 (  0) 0) |
| [2] |
Sanlaville E, Schmidt G. Machine scheduling with availability constraints. Acta Informatica, 1998, 35(9): 795-811. DOI:10.1007/s002360050143 (  0) 0) |
| [3] |
Kubzin M A, Strusevich V A. Planning machine maintenance in two-machine shop scheduling. Operations Research, 2006, 54(4): 789-800. DOI:10.1287/opre.1060.0301 (  0) 0) |
| [4] |
Ma Y, Chu C B, Zuo C R. A survey of scheduling with deterministic machine availability constraints. Computers & Industrial Engineering, 2010, 58(2): 199-211. DOI:10.1016/j.cie.2009.04.014 (  0) 0) |
| [5] |
Qi X, Chen T, Tu F. Scheduling the maintenance on a single machine. Journal of the Operational Research Society, 1999, 50(10): 1071-1078. DOI:10.1057/palgrave.jors.2600791 (  0) 0) |
| [6] |
Yang D-L, Hung C-L, Hsu C-J, et al. Minimizing the makespan in a single machine scheduling problem with a flexible maintenance. Journal of the Chinese Institute of Industrial Engineers, 2002, 19(1): 63-66. DOI:10.1080/10170660209509183 (  0) 0) |
| [7] |
Lee C-Y, Yu G. Single machine scheduling under potential disruption. Operations Research Letters, 2007, 35(4): 541-548. DOI:10.1016/j.orl.2006.08.005 (  0) 0) |
| [8] |
Lee C Y, Chen Z L. Scheduling jobs and maintenance activities on parallel machines. Naval Research Logistics (NRL), 2000, 47(2): 145-165. DOI:10.1002/(SICI)1520-6750(200003)47:2<145::AID-NAV5>3.0.CO;2-3 (  0) 0) |
| [9] |
Chen J-S. Optimization models for the machine scheduling problem with a single flexible maintenance activity. Engineering Optimization, 2006, 38(1): 53-71. DOI:10.1080/03052150500270594 (  0) 0) |
| [10] |
Chen J-S. Scheduling of nonresumable jobs and flexible maintenance activities on a single machine to minimize makespan. European Journal of Operational Research, 2008, 190(1): 90-102. DOI:10.1016/j.ejor.2007.06.029 (  0) 0) |
| [11] |
Sbihi M, Varnier C. Single-machine scheduling with periodic and flexible periodic maintenance to minimize maximum tardiness. Computers & Industrial Engineering, 2008, 55(4): 830-840. DOI:10.1016/j.cie.2008.03.005 (  0) 0) |
| [12] |
Mosheiov G, Sarig A. Scheduling a maintenance activity to minimize total weighted completion-time. Computers & Mathematics with Applications, 2009, 57(4): 619-623. DOI:10.1016/j.camwa.2008.11.008 (  0) 0) |
| [13] |
Levin A, Mosheiov G, Sarig A. Scheduling a maintenance activity on parallel identical machines. Naval Research Logistics (NRL), 2009, 56(1): 33-41. DOI:10.1002/nav.20324 (  0) 0) |
| [14] |
Chen W-J. Minimizing number of tardy jobs on a single machine subject to periodic maintenance. Omega, 2009, 37(3): 591-599. DOI:10.1016/j.omega.2008.01.001 (  0) 0) |
| [15] |
Batun S, Azizoǧlu M. Single machine scheduling with preventive maintenances. International Journal of Production Research, 2009, 47(7): 1753-1771. DOI:10.1080/00207540701636348 (  0) 0) |
| [16] |
Sun K, Li H. Scheduling problems with multiple maintenance activities and non-preemptive jobs on two identical parallel machines. International Journal of Production Economics, 2010, 124(1): 151-158. DOI:10.1016/j.ijpe.2009.10.018 (  0) 0) |
| [17] |
Low C, Ji M, Hsu C-J, et al. Minimizing the makespan in a single machine scheduling problems with flexible and periodic maintenance. Applied Mathematical Modelling, 2010, 34(2): 334-342. DOI:10.1016/j.apm.2009.04.014 (  0) 0) |
| [18] |
Yang S-L, Ma Y, Xu D-L, et al. Minimizing total completion time on a single machine with a flexible maintenance activity. Computers & Operations Research, 2011, 38(4): 755-770. DOI:10.1016/j.cor.2010.09.003 (  0) 0) |
| [19] |
Lee C-Y, Lin C-S. Single-machine scheduling with maintenance and repair rate-modifying activities. European Journal of Operational Research, 2001, 135(3): 493-513. DOI:10.1016/S0377-2217(00)00322-2 (  0) 0) |
| [20] |
Cassady C R, Kutanoglu E. Minimizing job tardiness using integrated preventive maintenance planning and production scheduling. IIE Transactions, 2003, 35(6): 503-513. DOI:10.1080/07408170304416 (  0) 0) |
| [21] |
Chen W J, Liao C J. Scheduling with different maintenance policies in a textile company. Journal of Quality in Maintenance Engineering, 2005, 11(1): 43-52. DOI:10.1108/13552510510589361 (  0) 0) |
| [22] |
Sortrakul N, Nachtmann H L, Cassady C R. Genetic algorithms for integrated preventive maintenance planning and production scheduling for a single machine. Computers in Industry, 2005, 56(2): 161-168. DOI:10.1016/j.compind.2004.06.005 (  0) 0) |
| [23] |
Jin Y, Jiang Z, Hou W. Multi-objective integrated optimization research on preventive maintenance planning and production scheduling for a single machine. The International Journal of Advanced Manufacturing Technology, 2008, 39(9): 954-964. DOI:10.1007/s00170-007-1268-5 (  0) 0) |
| [24] |
Pan E S, Liao W Z, Xi L F. Single-machine-based production scheduling model integrated preventive maintenance planning. The International Journal of Advanced Manufacturing Technology, 2010, 50(1): 365-375. DOI:10.1007/s00170-009-2514-9 (  0) 0) |
| [25] |
Pan E S, Liao W Z, Xi L F. A joint model of production scheduling and predictive maintenance for minimizing job tardiness. The International Journal of Advanced Manufacturing Technology, 2012, 60(9): 1049-1061. DOI:10.1007/s00170-011-3652-4 (  0) 0) |
| [26] |
Wang S J, Liu M. A branch and bound algorithm for single-machine production scheduling integrated with preventive maintenance planning. International Journal of Production Research, 2013, 51(3): 847-868. DOI:10.1080/00207543.2012.676683 (  0) 0) |
| [27] |
Cassady C R, Kutanoglu E. Integrating preventive maintenance planning and production scheduling for a single machine. IEEE Transactions on Reliability, 2005, 54(2): 304-309. DOI:10.1109/TR.2005.845967 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30


