Dynamics plays a pivotal role in understanding the RNNs. The studies about the RNNs' dynamics have been carried out for many years[1-7]. In spite of many progresses, the problem still remains unanswered. Moreover, this issue seems to become more and more complicated because of the emergence of RNNs with complex architectures[8-9]. ESN is a simple approach to design RNNs. The common idea of ESN is that input signals are fed into a fixed RNN (called reservoir), and then a trainable readout extracts the required features from the reservoir and generate the network output[10]. In the past ten years, ESN and its large amounts of variants have been successfully applied in modeling various time related tasks[11-14].
Despite of the simplicity, ESN's dynamics is still not fully understood[1, 15-16]. It results in the difficulty of designing the reservoir[15]. In recent years, theoretical studies about ESN, such as universal approximation[15], echo state property and Lyapunov exponents[17-18], have attracted more and more attention. However, these theoretical studies are not enough to reveal the ESN's dynamic behavior, because they cannot reflect the change law of the internal state of the ESN with time. A few studies about the internal dynamics only focus on shallow ESNs[4]. With the gradual emergence of ESNs with different structures, the dynamic of shallow ESN is not sufficient to explain the dynamic behavior of ESNs. Therefore, the authors of this paper investigate the dynamics of four representative ESNs proposed in the last 20 years that are conventional ESN (CESN)[19], ESN with a delay& sum readout (D & S ESN)[14], deep echo state network (DESN)[20], and asynchronously deep echo state network (ADESN)[21], respectively. Among these models, CESN and D & S ESN are shallow ESNs. Compared with CESN, the D & S ESN has extra delayed links attached to the reservoir neurons. DESN and ADESN are multilayered/deep ESNs proposed in recent years, which divide the single reservoir in CESN into a number of sub-reservoirs that are connected one by one in sequence. Extra delayed links are inserted between every two adjacent sub-reservoirs/layers in ADESN. The investigation is conducted from the spatial and temporal views. It is beneficial to build a unified theoretical framework for the dynamic study of ESNs. short-term memory (STM) is closely related to the ESN's dynamics[3, 7]. It is one of the key factors to solve time related tasks. Therefore, based on the dynamic analysis, the STM capacities of ESNs are studied through several numerical experiments. These experiments reveal the STM capacities of ESNs under different hyper-parameter settings. It is helpful to set appropriate hyper-parameters to obtain appropriate STM capacity for specific time-dependent problems.
The paper has mainly two contributions. One is to explain the dynamics of different ESNs under a unified theoretical framework. The other is to investigate the STM of ESNs under different hyper-parameters. The remainder of this paper is organized as follows. Section 1 introduces related works about the involved ESNs. Section 2 analyzes the dynamics of the ESNs based on linear system theory. In Section 3, STM is studied through several experiments based on the dynamic analysis. Also, theoretical conclusions are extended experimentally to nonlinear ESNs. In addition, the influence of the dynamics and STM on ESN's performance is further interpreted through two time series modeling tasks. Finally, some conclusions are made in Section 4.
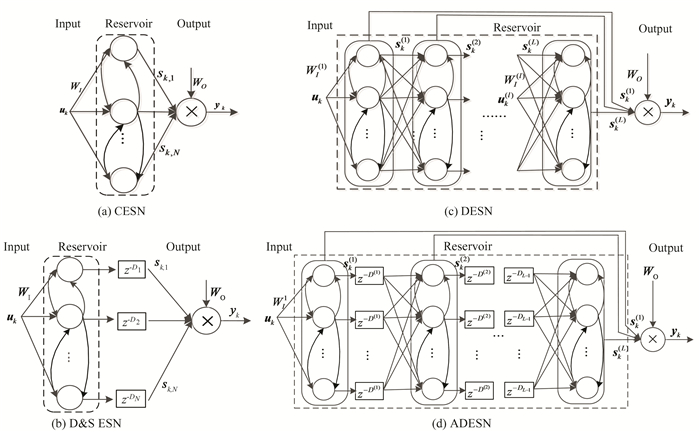
1 Related WorksThe dynamics of the CESN (Fig. 1(a)) can be expressed as
| $ \boldsymbol{s}_{k}=f\left(\alpha \boldsymbol{W}_{\mathrm{I}} \boldsymbol{u}_{k}+\boldsymbol{W}_{\mathrm{R}} \boldsymbol{s}_{k-1}\right) $ | (1) |
where k denotes time step, f is activation function, α is the input scaling,
|
Fig.1 Topologies of ESN models |
The output of the CESN is
| $ \boldsymbol{y}_{k}=\boldsymbol{W}_{o} \boldsymbol{s}_{k} $ | (2) |
where
The dynamics of D & S ESN (Fig. 1(b)) is the same as that of the CESN. But its output is a linear combination of the delayed sk, i.e.,
| $ \boldsymbol{y}_{k}=\sum\limits_{i=1}^{N} \boldsymbol{W}_{i, o} \boldsymbol{s}_{k-D_{i}, i} $ | (3) |
where Wi, O denotes the i-th column of WO.Di is the delayed time of the i-th neuron, and sk-j, i(j=D1, …, DN) is the delayed state of the i-th neuron.
The DESN is a multilayered ESN (Fig. 1(c)). The dynamics of the l-th layer can be expressed as
| $ \boldsymbol{s}_{k}^{(l)}=f\left(\alpha \boldsymbol{W}_{\mathrm{I}}^{(1)} \boldsymbol{u}_{k}^{(l)}+\boldsymbol{W}_{\mathrm{R}}^{(1)} \boldsymbol{s}_{k-1}^{(l)}\right) $ | (4) |
where
| $ \boldsymbol{u}_{k}^{(l)}=\left\{\begin{array}{l} \boldsymbol{u}_{k}, l=1 \\ \boldsymbol{s}_{k}^{(l-1)}, 1<l<L \end{array}\right. $ | (5) |
where l denotes the layer ID, sk(l) is the state of the l-th layer, WI(l) and WR(l) are the input weight matrix and the reservoir weight matrix of the l-th layer respectively, uk(l) is the external input of the l-th layer, and L is the amount of layer.
The output of the DESN is
| $ \boldsymbol{y}_{k}=\left[\begin{array}{lll} \boldsymbol{W}_{\rm O}^{(1)} & \cdots & \boldsymbol{W}_{\rm O}^{(L)} \end{array}\right]\left[\begin{array}{c} \boldsymbol{s}_{k}^{(1)} \\ \vdots \\ \boldsymbol{s}_{k}^{(L)} \end{array}\right] $ | (6) |
where WO(l) is the output weight matrix related to the l-th layer and its dimension is Q×N(l), N(l) is the reservoir size of the l-th layer.
The dynamics and the output of the ADESN (Fig. 1(d)) are the same as that of the DESN except uk(l). Because of the existence of the delayed links, uk(l) in the ADESN is
| $ \boldsymbol{u}_{k}^{(l)}=\left\{\begin{array}{l} \boldsymbol{u}_{k}, l=1 \\ \boldsymbol{s}_{k-D^{(l-1)}}^{(l-1)}, 1<l<L \end{array}\right. $ | (7) |
where D(l) is the delayed time between the l-th layer and the (l+1)-th layer.
2 Dynamic Investigation of ESNsIn this section, the dynamics of the involved ESNs is investigated by the linear system theory. The conclusions deduced by the linear system theory will extend to the nonlinear ESNs experimentally in the next part. To reduce the complexity, it is assumed that f is an identity function in this section. In addition, suppose uk≡ 0 when k≤0.
2.1 Dynamics of CESN and D & S ESNWhen f=1, the dynamics of the CESN (Eq.(1)) can be rewritten as
| $ \begin{aligned} \boldsymbol{s}_{k}= & \alpha \boldsymbol{W}_{\mathrm{I}} \boldsymbol{u}_{k}+\boldsymbol{W}_{\mathrm{R}} \boldsymbol{s}_{k-1}=\alpha \boldsymbol{W}_{\mathrm{I}} \boldsymbol{u}_{k}+\alpha \boldsymbol{W}_{\mathrm{R}} \boldsymbol{W}_{\mathrm{I}} \boldsymbol{u}_{k-1}+ \\ & \boldsymbol{W}_{\mathrm{R}}^{2} \boldsymbol{s}_{k-2} \end{aligned} $ | (8) |
By analogy, one can conclude that
| $ \boldsymbol{s}_{k}=\boldsymbol{W}_{\mathrm{R}}^{k} \boldsymbol{S}_{0}+\sum\limits_{d=0}^{k-1} \alpha \boldsymbol{W}_{\mathrm{R}}^{d} \boldsymbol{W}_{\mathrm{I}} \boldsymbol{u}_{k-d} $ | (9) |
where d denotes the delayed time step.
Because
| $ \boldsymbol{s}_{k}=\alpha \sum\limits_{d=0}^{k-1} \beta_{d} \boldsymbol{u}_{k-d} $ | (10) |
where
| $ \beta_{d}=\boldsymbol{W}_{\mathrm{R}}^{d} \boldsymbol{W}_{\mathrm{I}} $ | (11) |
Similarly, the dynamics of the D & S ESN is as follows:
| $ \boldsymbol{s}_{k, i}=\alpha \sum\limits_{d=0}^{k-D_{i}-1} \beta_{d, i} \boldsymbol{u}_{k-D_{i}-d} $ | (12) |
where βd, i is the i-th row of βd.
2.2 Dynamics of DESN and ADESNFollowing Eqs. (8) and (9), when f is identity function, the state of the l-th layer of the ADESN is
| $ \boldsymbol{s}_{k}^{(l)}=\left(\boldsymbol{W}_{\mathrm{R}}^{(l)}\right)^{k} \boldsymbol{s}_{0}^{(l)}+\alpha \sum\limits_{d=0}^{k-1}\left(\boldsymbol{W}_{\mathrm{R}}^{(l)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(l)} \boldsymbol{u}_{k-d}^{(l)} $ | (13) |
If
| $ \boldsymbol{s}_{k}^{(l)}=\alpha \sum\limits_{d=0}^{k-1}\left(\boldsymbol{W}_{\mathrm{R}}^{(l)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(l)} \boldsymbol{u}_{k-d}^{(l)} $ | (14) |
For l=1,
| $ \boldsymbol{s}_{k}^{(1)}=\alpha \sum\limits_{d=0}^{k-1}\left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(1)} \boldsymbol{u}_{k-d} $ | (15) |
For l=2,
| $ \boldsymbol{s}_k^{(2)}=\alpha \sum\limits_{d=0}^{k-D^{(1)}-1}\left(\boldsymbol{W}_{\mathrm{R}}^{(2)}\right)^d \boldsymbol{W}_{\mathrm{I}}^{(2)} \boldsymbol{u}_{k-d}^{(2)} $ | (16) |
Substituting Eq. (7) into Eq. (16) yields
| $ \begin{aligned} \boldsymbol{s}_{k}^{(2)} & =\alpha \sum\limits_{d=0}^{k-D^{(1)}-1}\left(\boldsymbol{W}_{\mathrm{R}}^{(2)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(2)} \boldsymbol{s}_{k-D^{(1)}-d}^{(1)}= \\ & \alpha \boldsymbol{W}_{\mathrm{I}}^{(2)} \boldsymbol{s}_{k-D^{(1)}}^{(1)}+\cdots+\alpha\left(\boldsymbol{W}_{\mathrm{R}}^{(2)}\right)^{k-D^{(1)}-1} \boldsymbol{W}_{\mathrm{I}}^{(2)} \boldsymbol{s}_{1}^{(1)} \end{aligned} $ | (17) |
According to Eq. (15),
| $ \boldsymbol{s}_{k-D^{(1)}-j}^{(1)}=\sum\limits_{d=0}^{k-D^{(1)}-j-1} \alpha\left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(1)} \boldsymbol{u}_{k-D^{(1)}-j-d} $ | (18) |
Note that uk ≡ 0 when k≤0. Substituting Eq. (18) into Eq. (17) yields
| $ \begin{gathered} \boldsymbol{s}_{k}^{(2)}=\alpha^{2}\left(\boldsymbol{W}_{\mathrm{R}}^{(2)}\right)^{k-D^{(1)}-1} \boldsymbol{W}_{\mathrm{I}}^{(2)} \boldsymbol{W}_{\mathrm{I}}^{(1)} \boldsymbol{u}_{1}+\cdots+ \\ \alpha^{2} \boldsymbol{W}_{\mathrm{I}}^{(2)} \sum\limits_{d=0}^{k-D^{(1)}-1}\left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(1)} \boldsymbol{u}_{k-D^{(1)-d}} \end{gathered} $ | (19) |
Expanding Eq.(19) and merging similar items in chronological order yields
| $ \boldsymbol{s}_{k}^{(2)}=\alpha^{2} \sum\limits_{d=0}^{k-D^{(1)}-1} \boldsymbol{\beta}_{d}^{(2)} \boldsymbol{u}_{k-D^{(1)}-d} $ | (20) |
where
| $ \boldsymbol{\beta}_{d}^{(2)}=\sum\limits_{j=0}^{d}\left(\boldsymbol{W}_{\mathrm{R}}^{(2)}\right)^{j} \boldsymbol{W}_{\mathrm{I}}^{(2)}\left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right)^{d-j} \boldsymbol{W}_{\mathrm{I}}^{(1)} $ | (21) |
By analogy, one can conclude that
| $ \boldsymbol{s}_{k}^{(1)}=\alpha^{l} \sum\limits_{d=0}^{k-\sum D^{(l)}-1} \boldsymbol{\beta}_{d}^{(l)} \boldsymbol{u}_{k-\sum D^{(l)-d}} $ | (22) |
where
| $ \boldsymbol{\beta}_{d}^{(l)}=\left\{\begin{array}{l} \left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(1)}, l=1 \\ \sum\limits_{j=0}^{d}\left(\boldsymbol{W}_{\mathrm{R}}^{(l)}\right)^{j} \boldsymbol{W}_{\mathrm{I}}^{(l)} \boldsymbol{\beta}_{d-j}^{(l-1)}, l>1 \end{array}\right. $ | (23) |
and
| $ \sum D^{(l)}=\sum\limits_{j=1}^{l-1} D^{(j)} $ | (24) |
The DESN is exactly a special case with D(l)=0 for all l. Hence the state of the l-th layer in the DESN is
| $ \boldsymbol{s}_{k}^{(l)}=\alpha^{l} \sum\limits_{d=0}^{k-1} \beta_{d}^{(l)} \boldsymbol{u}_{k-d} $ | (25) |
According to Eqs. (10), (12), (22) and (25), the states of ESNs are exactly the superpositions of the delayed input features. For the CESN and the DESN (Eqs. (10) and (22)), the superposition features contain all the input history from time step k to time step 1. i.e., the current state sk contains the features of
From Eq. (10), βduk-d is the d-th item of the right side of equation. It can be regarded as the spatial features that are extracted by the reservoir neurons from the external input at time step k-d. These spatial features of the external inputs at different time steps forms the current state. Therefore, the CESN has spatiotemporal characteristic. The other ESNs have the similar spatial characteristics as the CESN. In this sense, βd can be regarded as a spatial mapping of the external input at time step k-d and it maps uk-d into a N-dimensional space.
2.3 Property of βdβd is a key factor to affect the dynamics of the ESNs. If ||βd|| is obviously larger than others, the features of uk-d are significant in the state. Conversely, the features of uk-d are weak in the state. Empirically speaking, significant features are easy to be captured by the readout from the states. Hence, if uk-d is pivotal to model a time related task, ||βd|| should be large.
Proposition 1 If
Proof
| $ \lim\limits_{d \rightarrow \infty}\left\|\beta_{d}\right\|=\lim\limits_{d \rightarrow \infty}\left\|\boldsymbol{W}_{\mathrm{R}}^{d} \boldsymbol{W}_{\mathrm{I}}\right\| \leqslant \lim\limits_{d \rightarrow \infty}\left\|\boldsymbol{W}_{\mathrm{I}}\right\|\left\|\boldsymbol{W}_{\mathrm{R}}^{d}\right\| $ | (26) |
According to Gelfand theorem,
| $ \lim\limits_{d \rightarrow \infty}\left\|\boldsymbol{W}_{\mathrm{R}}^{d}\right\|=\lim\limits_{d \rightarrow \infty} \rho^{d}\left(\boldsymbol{W}_{\mathrm{R}}\right) $ | (27) |
Because
| $ \lim\limits_{d \rightarrow \infty}\left\|\beta_{d}\right\|=0 $ | (28) |
This completes the proof.
‖βd, i‖ in Eq. (12) also satisfies Proposition 1 because βd, i is the i-row of the βd.
Proposition 2 When the maximum singular value of WR is smaller than 1, ||βd|| in Eq. (11) is monotonically decreasing as d increases.
Proof The maximum singular value of WR is ‖WR‖2. If ‖WR‖2 < 1, the CESN has ESP. According to Eq. (11),
| $ \begin{aligned} & \left\|\beta_{d+1}\right\|_{2}=\left\|\boldsymbol{W}_{\mathrm{R}}^{d+1} \boldsymbol{W}_{\mathrm{I}}\right\|_{2} \leqslant \\ & \left\|\boldsymbol{W}_{\mathrm{R}}^{d} \boldsymbol{W}_{\mathrm{I}}\right\|_{2}\left\|\boldsymbol{W}_{\mathrm{R}}\right\|_{2}=\left\|\beta_{d}\right\|_{2}\left\|\boldsymbol{W}_{\mathrm{R}}\right\|_{2}< \\ & \left\|\beta_{d}\right\|_{2} \end{aligned} $ | (29) |
This completes the proof.
Proposition 3 If
Proof: When l=1,
| $ \begin{aligned} \lim\limits_{d \rightarrow \infty}&\left\|\beta_{d}^{(1)}\right\|=\\ &\lim\limits_{d \rightarrow \infty}\left\|\left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right)^{d} \boldsymbol{W}_{\mathrm{I}}^{(1)}\right\| \leqslant \lim\limits_{d \rightarrow \infty}\left\|\boldsymbol{W}_{\mathrm{I}}^{(1)}\right\| \rho^{d}\left(\boldsymbol{W}_{\mathrm{R}}^{(1)}\right) \end{aligned} $ | (30) |
Because
| $ \lim\limits_{d \rightarrow \infty}\left\|\beta_{d}^{(1)}\right\|=0 $ | (31) |
Suppose l=m(m < L),
| $ \lim\limits_{d \rightarrow \infty}\left\|\beta_{d}^{(m)}\right\|=0 $ | (32) |
When l=m+1,
| $ \begin{aligned} &\left\|\beta_{d}^{(m+1)}\right\|=\left\|\sum\limits_{j=0}^{d}\left(\boldsymbol{W}_{\mathrm{R}}^{(m+1)}\right)^{d-j} \boldsymbol{W}_{\mathrm{I}}^{(m+1)} \beta_{j}^{(m)}\right\| \leqslant \\ &\ \ \ \ \ \ \left\|\boldsymbol{W}_{\mathrm{I}}^{(m+1)}\right\|\left(\left\|\beta_{0}^{(m)}\right\| \rho^{d}\left(\boldsymbol{W}_{\mathrm{R}}^{(m+1)}\right)+\cdots+\right. \\ &\ \ \ \ \ \ \left.\left\|\beta_{d}^{(m)}\right\|\right) \end{aligned} $ | (33) |
According to Eq.(32) and
| $ \lim\limits_{d \rightarrow \infty}\left\|\beta_{d}^{(m+1)}\right\|=0 $ | (34) |
This completes the proof.
Propositions 1 and 3 indicate that the norms of the spatial mapping matrices of all involved ESNs are decreasing as d increases in general trends. Under this condition, sk can be approximated by the front H items, i.e., Eqs. (10), (12), (22) and (25) can be approximated by Eqs. (35), (36), (37) and (38) respectively.
| $ \boldsymbol{s}_{k}=\sum\limits_{d=0}^{H} \beta_{d} \boldsymbol{u}_{k-d} $ | (35) |
| $ \boldsymbol{s}_{k, i}=\sum\limits_{d=0}^{H} \beta_{d, i} \boldsymbol{u}_{k-D_{i}-d} $ | (36) |
| $ \boldsymbol{s}_{k}^{(l)}=\sum\limits_{d=0}^{H} \boldsymbol{\beta}_{d}^{(l)} \boldsymbol{u}_{k-\sum D^{(l)-d}} $ | (37) |
| $ \boldsymbol{s}_{k}^{(l)}=\sum\limits_{d=0}^{H} \boldsymbol{\beta}_{d}^{(l)} \boldsymbol{u}_{k-d} $ | (38) |
where H is a sufficiently large positive integer.
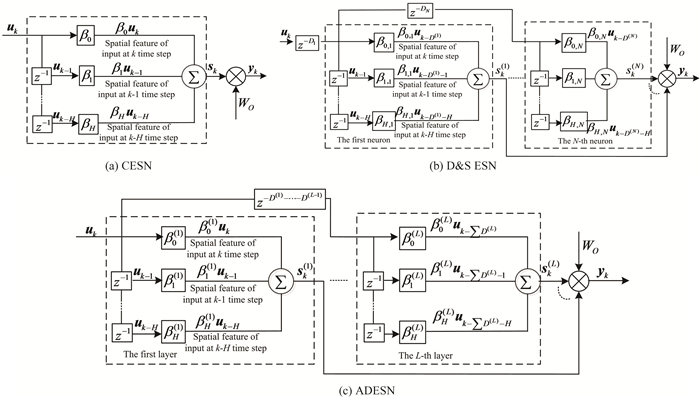
Eqs. (35)-(38) imply that the current states of ESNs contain practically only limited input information. The equations can be exhibited in expanding forms as shown in Fig. 2. If D(l) is set as zero for all l, ADESN becomes the DESN. Hence, the topology of the DESN is not listed in Fig. 2.
|
Fig.2 Equivalent topologies of linear ESNs |
From Fig. 2 (a), sk in the CESN is a superstition of the spatial features of the external inputs at time steps from k to k-H. Comparison of Figs. 2(a) and (c) show ADESN is equivalent to be composed of several CESNs in parallel connections, and the external input of the l-th(l>1) CESN is u(k-∑D(l)). For the D & S ESN, the equivalent external input of the i-th neuron is u(k-Di). From Fig. 2(b) and Fig. 2(c), the D & S ESN and the ADESN are highly similar in topologies. The D & S ESN is equivalent to an N-layer ADESN in appearance. However, there are significant difference between them. First, there is only one neuron in each layer of the D & S ESN, while the reservoir in each layer of ADESN is composed of a number of neurons. Second, βd, i in the D & S ESN is exactly the i-row of βd which is the spatial mapping matrix of a CESN, while βd(l) in the ADESN is the spatial mapping matrix of the l-layer. According to Fig. 2(c) and D(l) =0 for all l, the DESN is equivalent to be composed of several CESNs in parallel connections, and the external inputs of all the CESNs are u(k).
Proposition 4 For the CESN, βN can be expressed by β0, …, βN-1.
Proof According to Cayley-Hamilton theory,
| $ \boldsymbol{W}_{\mathrm{R}}^{N}+k_{N} \boldsymbol{W}_{\mathrm{R}}^{N-1}+\cdots+k_{1} \boldsymbol{I}=0 $ | (39) |
where ki (i=1, …, N) are the coefficient of the characteristic polynomial of WR. Eq.(39) can be written as
| $ \boldsymbol{W}_{\mathrm{R}}^{N}=-k_{1} \boldsymbol{I}-k_{2} \boldsymbol{W}_{\mathrm{R}} \cdots-k_{N} \boldsymbol{W}_{\mathrm{R}}^{N-1} $ | (40) |
Substituting Eq. (40) into Eq. (11) yields
| $ \begin{aligned} & \boldsymbol{\beta}_{N}=\boldsymbol{W}_{\mathrm{R}}^{N} \boldsymbol{W}_{\mathrm{I}}= \\ & \quad\left(-a_{1} \boldsymbol{I}-\mathrm{a}_{2} \boldsymbol{W}_{\mathrm{R}} \cdots-a_{N} \boldsymbol{W}_{\mathrm{R}}^{N-1}\right) \boldsymbol{W}_{\mathrm{I}}= \\ & \quad-a_{1} \beta_{0}-\cdots-a_{N} \beta_{N-1} \end{aligned} $ | (41) |
where ai(i=1, …, N) are real values. This completes the proof.
Proposition 4 can be extended to the first layers of DESN and ADESN, because both of them are equivalent to a CESN. Proposition 4 also implies that βd(d≥N) can be expressed by β0, …, βN-1.
2.4 Temporal FeaturesAccording to Eq. (35), sk in the CESN contains the features of inputs at time steps from k to k-H. On the surface, the readout can recall uk to uk-H in the states. However, it is usually not true in practice. It will be explained next.
Definition 1 If the readout can recall accurately uk-d from the state, Eq.(42) must hold.
| $ \boldsymbol{u}_{k-d}=\boldsymbol{W}_{\rm O} \boldsymbol{s}_{k} $ | (42) |
Proposition 5 Suppose uk obeys random distribution. If uk-d can be recalled from the states of the CESN accurately, d < N, where N is the reservoir size.
Proof: Substituting Eq. (35) into Eq.(42) yields
| $ \begin{aligned} \boldsymbol{u}_{k-d}= & \boldsymbol{W}_{\rm O} \sum\limits_{j=0}^{H} \beta_{d} \boldsymbol{u}_{k-d}=\boldsymbol{W}_{\rm O} \boldsymbol{\beta}_{0} \boldsymbol{u}_{k}+\cdots+ \\ & \boldsymbol{W}_{\rm O} \boldsymbol{\beta}_{d} \boldsymbol{u}_{k-d}+\cdots+\boldsymbol{W}_{\rm O} \boldsymbol{\beta}_{H} \boldsymbol{u}_{k-H} \end{aligned} $ | (43) |
Because uk obeys random distribution, the necessary condition for Eq. (43) to hold is
| $ \boldsymbol{W}_{\rm O} \beta_{j}=\left\{\begin{array}{l} I, j=d \\ 0, \text { otherwise } \end{array}\right. $ | (44) |
According to Proposition 4, if d≥N,
| $ \beta_{d}=a_{1} \beta_{0}+\cdots+a_{N} \beta_{N-1} $ | (45) |
Therefore, when d≥N,
| $ \boldsymbol{W}_{\rm O} \boldsymbol{\beta}_{d}=a_{1} \boldsymbol{W}_{\rm O} \boldsymbol{\beta}_{0}+\cdots+a_{N} \boldsymbol{W}_{\rm O} \boldsymbol{\beta}_{N-1} $ | (46) |
Obviously, when d≥N, Eq.(46) is contradicted to Eq.(44), i.e., when d≥N, Eq.(44) cannot hold. It means that the readout cannot recall accurately uk-d from sk when d≥N. This completes the proof.
STM plays a pivotal role for ESNs to model time related tasks. It is the capacity for holding a small amount of information in mind in an active, readily available state for a short period of time[22]. Proposition 5 implies that the accurate STM capacity is not larger than the reservoir size for a random input sequence. This conclusion is also proved by a statistical theory[7]. Proposition 5 is applicable to the first layers of the DESN and the ADESN. For the deeper layers, this proposition can hardly be verified theoretically because of its complexity. However, in the experiments, it is found that Proposition 5 is still valid to the deeper layers in general trends. The related experiments are exhibited in the following section.
There is significant difference among ESNs in STM modes. For the CESN, the reservoir can preserve the input features at time steps from k to k-MC, where MC (memory capacity) is the real STM capacity. According to Proposition 5, MC≤N. For the DESN, the equivalent external input in each layer is uk. Hence each layer in the DESN can preserve the input features at time steps from k to k-MC(l), where MC(l) is the real STM capacity of the l-th layer in the DESN. Because the memory starting time in the layers of DESN are the same, there are a large number of duplicate memories among layers of the DESN. For the D & S ESN, the reservoir can preserve the input features at time steps k-D1, …, k-DN. If Di(i=1, …, N) are selected carefully, the D & S ESN can preserve the required input features. However, there are only one neuron to extract and preserve the input features at k-Di. Therefore, the spatial features of the input at k-Di time step are very one-sided. A possible way to solve this problem is to divide the reservoir neurons into several groups and each group adopts the same delayed time. According to Fig. 2, the external input of the l-th layer in ADESN is equivalent to u(k-∑D(l)). Therefore, the l-th layer can preserve the input features at time steps from k-∑D(l) to k-∑D(l)-MC(l). The layers of ADESN have different memory timespans. It can generate a relay memory mode that can reduce the duplicate memories and enlarge the STM capacity.
3 Experiments and Analysis 3.1 Changes of ||βd|| with dβd is a pivotal parameter that controls the decay rate of the features of uk-d. According to Eq.(23), βd is determined by the parameters including WR, WI, and the delayed time d. It is irrelevant to the external input and the other parameters (for example D(l)). In this sense, ‖βd(l)‖ in ADESN and DESN have the same changing trends. Therefore, CESN and DESN are selected to investigate the changes of ‖βd(l)‖ with d. Table 1 lists the parameter settings.
| Table 1 Experimental settings for CESN and DESN |
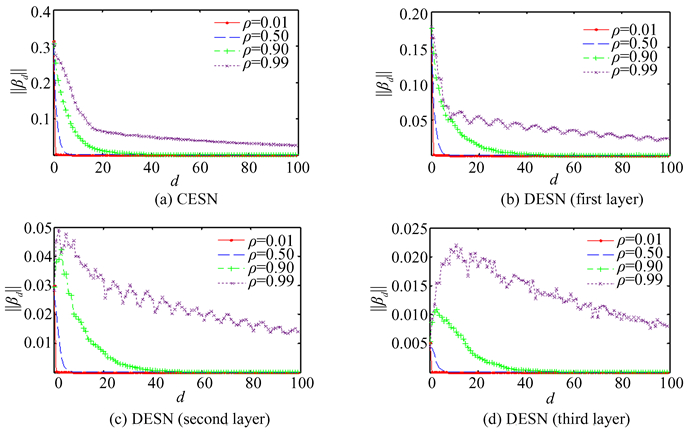
To reduce the influence of randomness, each test is carried out 10 times independently and the mean value is regarded as the final testing results. Fig. 3 shows the results under different spectral radii. From Fig. 3(a), ρ(WR) (denoted as ρ for simplicity) is a key parameter that affects ||βd|| significantly. When ρ is small, ||βd|| decays very rapidly. The decay rate of ||βd|| becomes slower and slower as ρ grows. From Figs. 3(b), (c) and (d), the ‖βd(l)‖(l= 1, 2, 3) in the DESN have the same changing trend as that in CESN. However, the changes of ‖βd(l)‖ with d in the second layer (Fig. 3(b)) and the third layer (Fig. 3(c)) are more complicated than that in the first layer because of the complexity of βd in the deeper layers. Nevertheless, the general change trends of ||βd|| with d are still descending when ρ < 1. Moreover, when ρ is properly small, ||βd|| is monotonically decreasing.
|
Fig.3 changes of ‖βd(l)‖ with d |
3.2 Testing STM
For most time dynamic tasks, the current output is determined by the inputs and outputs in the recent time. They can be described as
| $ \begin{aligned} y(k)= & F\left(u(k), \cdots, u\left(k-T_{1}\right), y(k-1), \cdots, \right. \\ & \left.y\left(k-T_{2}\right)\right) \end{aligned} $ | (47) |
where T1 and T2 is the delayed time, and F is an unknown function.
Without considering the initial state, Eq. (47) is equivalent to
| $ y(k)=F\left(u(k), \cdots, u\left(k-T_{3}\right)\right) $ | (48) |
where T3 denotes the delayed time.
Eq. (48) implies that the current output y(k) is determined by the inputs in the recently past time. To model such dynamic system, the ESN should memorize the recent input characteristics in its reservoir states, and these preserved input characteristics in the reservoir states should be sufficient to construct y(k). This memory is called STM. STM is closely related to the reservoir dynamics. It is necessary to set an appropriate STM capacity for a given time-dependent task, and some tasks need large STM capacities while other tasks need small ones.
In Ref. [7], an estimation method about STM for the CESN is proposed as follows:
| $ \mathrm{MC}=\sum\limits_{d=0}^{\infty} \mathrm{MC}_{d} $ | (49) |
where
| $ \mathrm{MC}_{d}=\frac{\operatorname{cov}^{2}\left(u(k-d), y_{d}(k)\right)}{\sigma^{2}(u(k-d)) \sigma^{2}\left(y_{d}(k)\right)} $ | (50) |
where yd(k) denotes the output of the readout unit trained to recall the input signal with a delay d, i.e., u(k-d), and cov2 and σ2 denote respectively the covariance and variance operators. MCd is an index that assesses the correlation between u(k-d) and yd(k).
In this experiment, u(k) is randomly sampled from a uniform distribution over interval [-0.5, 0.5]. WI(l) are randomly sampled over interval [-1, 1] for all l. The aim is to train the ESNs to output u(k-d) (d=0, 1, …, ∞) with the input u(k), which attempts to reconstruct the delayed input u(k-d). Practically, the upper limit of d is set as 100, since the recall performance in ESNs will drop drastically when more time steps are predicted than the number of neurons in the reservoir. The parameter settings of the CESN and the DESN are listed in Table 1. For the D & S ESN, the reservoir neurons are divided into three groups and each group has 10 neurons. The delayed time of the first, second and third groups are 0, 20 and 40 respectively. The other parameters of the D & S ESN are the same as that of the CESN. The parameters of the ADESN are the same as that of the DESN except that D(l)=20 (l=1, 2). 2500 samples are further generated. The first 2000 samples are used to train the models, and the remaining 500 samples are used to calculate MCd and MC. The first 500 steps in the training sequence are used as the washout phase to eliminate the influence of the initial state.
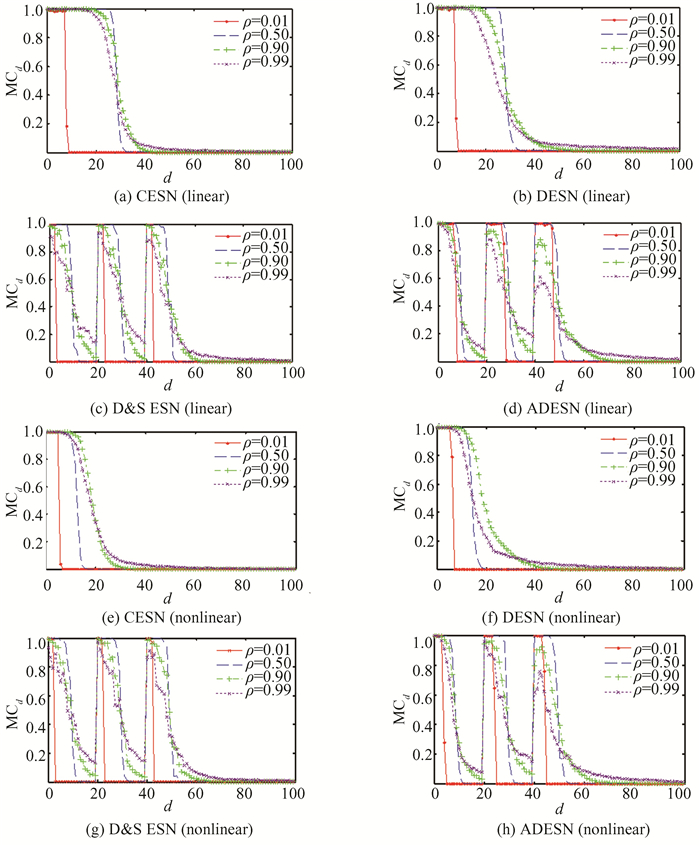
Fig. 4 shows the changes of MCd with d for ESNs. From Fig. 4(a) and Fig. 4(b), the CESN and DESN exhibit almost the same memory characteristics. When ρ is small (for example ρ=0.01), the CESN and DESN memorize a little input history accurately and the memory is sharply cut-off at a certain point. When ρ=0.5, the readout can recall more input history accurately. If ρ grows continuously (ρ=0.9, 0.99), MCd decays slowly. The recalling precision reduces though the readout can recall more input history. From Fig. 4(c) and Fig. 4(d), the D & S ESN and ADESN exhibit almost the same memory property, and each group of the D & S ESN or each layer of ADESN exhibits almost the same memory property as the CESN. The D & S ESN and the ADESN have the characteristics of segmented memory. According to Proposition 5, for the ADESN, when D(l)≥N(l), there is clear boundary in memory spans between the l-th layer and the (l+1)-th layer. When D(l) < N(l), the boundary is indistinct, because there are overlapped area between the memory spans of the l-th layer and the (l+1)-th layer. For the ADESN, the amplitudes of the input features shrink layer by layer if the input scaling is less than 1.
|
Fig.4 Changes of MCd with d |
Therefore, it is more difficult to extract accurately the input features from the deeper layers than the shallower layers. However, for most of time prediction tasks, the recent input history is more important than the remote one. The memory decreasing layer by layer in the ADESN just fits the concept.
Figs. 4(e), (f), (g) and (h) are respectively the nonlinear versions of Figs. 4 (a), (b), (c) and (d). In the nonlinear versions, the reservoir neurons adopt tanh activation functions. From Figs. 4 (e) and (f), the memory time in the nonlinear versions of CESN and DESN is significantly shorter than their linear ones. It is also called memory-nonlinearity trade-off[23]. From Figs. 4(c) and (g), the memory-nonlinearity trade-off in the D & S ESN is not apparent. For the ADESN, the memory-nonlinearity trade-off is clear when ρ is small, but it becomes inapparent when ρ is properly large.
Reservoir size is another important parameter to affect the STM capacity. Fig. 5(a) shows the changes of MC with the reservoir size. Generally, the MC increases with the growth of the reservoir size. However, the growth of MC with reservoir size is not linear. It is slower and slower as the reservoir size grows. Moreover, the D & S ESN and the ADESN achieve obviously much larger MC than the CESN and DESN under the same reservoir size.
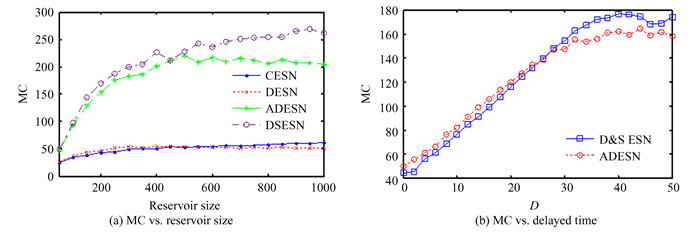
|
Fig.5 Changes of MC with the reservoir size and changes of MC with the delayed time in D & S ESN and ADESN |
Fig. 5(b) shows the changes of MC with the delayed time. In this experiment, the reservoir size is set as 200. The spectral radius is 0.9, and the input scaling is 0.1. The reservoir neurons in the ADESN and the D & S ESN are divided into five layers and five groups respectively. In the ADESN, the delayed time (denoted as D) between every two adjacent layers increases from 0 to 50 with incremental step 2. In the D & S ESN, the delayed time of the i-th group is (i-1)×D. When D is small, the MC increases with D nearly linearly. When D is larger than a threshold (the maximum value is the reservoir size of each layer/group), the MC reaches a plateau. Compared with the CESN and the DESN, the D & S ESN and the ADESN have an extra parameter (delayed time) to adjust the MC in a large scale under the constant reservoir size. What is more, the D & S ESN and the ADESN can adjust the memory timespans by adapting the delayed time, and these timespans can form a continuous memory or a series of discrete memory segments, while the CESN and the DESN can only have a continuous memory span. Hence, the memory in the D & S ESN and the ADESN are more flexible than the CESN and the DESN. A number of samples have verified the advantages of the D & S ESN and the ADESN on solving long-term dependent tasks[14, 21].
STM is a key factor to affect the performance of ESNs. In Section 3.3 and Section 3.4, this point will be explained through two applications.
3.3 Mackey-Glass System PredictionThe Mackey-Glass time series model can be expressed by the following equation[14] :
| $ \dot{y}(t)=\frac{0.2 y(t-\tau)}{1+y^{10}(t-\tau)}-0.1 y(t) $ | (51) |
The system has a chaotic attractor if τ>16.8. In this paper, τ is set as τ=30. The Mackey-Glass model can be written as a discrete form:
| $ y(k)=F(u(k-1), u(k-T), \cdots, u(k-Q T)) $ | (52) |
where T is the delayed time and Q is a positive integer. For such model, a series of discrete STM segments are very suitable. D & S ESN and ADESN can realize this memory mode, while CESN and DESN can realize only a continuous memory. According to Proposition 2, when D=T, D & S ESN and ADESN can extract u(k-iT) (i=1, …, Q) precisely from the reservoir states. 3500 samples are generated in total. The first 500 steps are as the wash-out phase, and the ESNs are trained by the next 2000 steps. The remaining 1000 steps are used to test the ESNs. The NRMSE is calculated by the first 500-step samples in the testing set. In the training process, the external input is u(k)=y(k-1), and the expected output is y(k). In the testing process, the prediction output at the previous step is fed back into the network, i.e., the network disconnects from the teacher signal and performs predictions independently in the testing procedure. The parameter settings are as follows: the reservoir size is 1000, the spectral radius is 0.99, the input scaling is 0.5. For CESN and ADESN, the layer number is 5, and the delayed time is 13 for ADESN. The testing results are shown in Table 2 and Fig. 6.
| Table 2 Testing results of different RC models for Mackey-Glass time series prediction tasks |
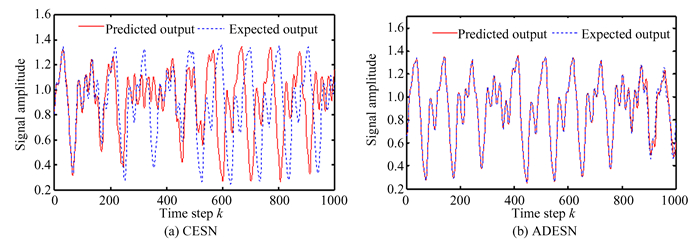
|
Fig.6 Testing results of ESNs for Mackey-Glass task |
From Table 2, the performance of D & S ESN and ADESN are better than that of CESN and DESN. From Fig. 2(b), the D & S ESN is equivalent to a multilayered ESN, and each layer has only one neuron. Therefore, the D & S ESN is insufficient in spatial mapping ability though it is sufficient in the temporal one, i.e., the D & S ESN cannot preserve the characteristics of u(k-T), …, u(k-QT) comprehensively. The ADESN avoids this defect. Hence, the ADESN achieves better results than the D & S ESN in this problem. Fig. 6 shows the prediction circles of CESN and ADESN. The CESN predicts the M-G model accurately only in a short time. As time pass by, the error between the CESN and the actual M-G model is getting bigger and bigger. By comparison, the ADESN predicts the M-G model accurately for a long time.
3.4 Modeling SO2 Concentration in Sulfur Recovery UnitSulfur recovery unit (SRU) is an important refinery processing module. It removes environmental pollutants from acid gas streams before they are released into the atmosphere[24]. Hydrogen sulfide and sulfur dioxide cause frequent damage to on-line analyzers, which often have to be taken off for maintenance. Therefore, it is necessary to design soft sensors that predict SO2 concentrations in the tail gas stream. There are five components in the input u(Table 3).
| Table 3 Descriptions of input components |
In this experiment, 10081 data are collected from the historical database of the plant. The first 8000 samples are selected as the training set, and the remainder of the samples are selected as the testing set. The parameter settings are as follows: the reservoir size is 100, the spectral radius is 0.8, the input scaling is 0.5. For CESN and ADESN, the layer number is 5, and the delayed time is 5 for ADESN. The testing results are shown in Table 4.
| Table 4 Performance comparison of ESN models (MSE denotes mean square error and R denotes correlation coefficient) |
Overall, the D & S ESN and the ADESN achieve better performance than the CESN and DESN. It contributes to the flexible STM in the D & S ESN and the ADESN. Moreover, ADESN can generate richer dynamics than D & S ESN because of large amounts of neurons in each layer. CESN or DESN is actually a special case of ADESN. Large number of time dependent tasks can be described by the same moving average model as shown in Eq. (52). When T and Q are small, CESN and DESN can achieve good performance because a continuously small STM is sufficient to this problem. When T or Q is big, CESN and DESN hardly achieve high performance, because u(k-QT) is difficult to be extracted from the reservoir states. ADESN solves this difficulty by a segmented memory method. Therefore, for most problems, the performance of ADESN is better than that of CESN and DESN. From structural view, CESN and DESN are actually special cases of ADESN.
4 ConclusionsThis paper investigates the dynamics of four kinds of ESNs which are proposed one after another in the past twenty years. The investigation reveals that the ESNs have spatiotemporal features in their dynamics, and the current state is exactly the superstition of the spatial features of the historical inputs at different time steps.
For a given time-related task, the significance and sufficiency of the required input features implied in the states are the two important issues. A large STM capacity can ensure the sufficiency of the required input features, because it implies that the states contain more input history. The CESN and DESN hardly generate large STM capacity, hence they are difficult to solve the tasks that required long input history. The significance of the required features is another problem that the CESN and DESN need to face. If the feature of u(k-d) is important to a model, ‖βd‖ should be large. This is not an easy thing for the CESN and DESN because of exponentially attenuation of ‖βd‖ with d. ADESN and D & S ESN solve this problem by inserting delay links between every two adjacent layers and by adding delayed links after reservoir neurons respectively. It breaks the attenuation continuity of ‖βd‖ with d and provides the possibility to increase ‖βd‖ corresponding to the key features by adapting the delayed time. In view of this, the ADESN achieves better performance for time-dependent tasks than the CESN and DESN. Compared with D & S ESN, ADESN can still have better results because it has more neurons in each layer while the D & S ESN has only one neuron in each layer. Therefore, ADESN generate richer dynamics than D & S ESN. From structural view, ADESN is an extension of CESN and DESN, and CESN or DESN is only a special case of ADESN. Therefore, ADESN is worth studying to find general dynamic characteristics in ESN. Nevertheless, the dynamical analysis about RNN is very complicated. We think there is still a long way to go concerning the dynamical research of the ESNs, especially for the deeper layers in ADESN.
| [1] |
Ceni A, Ashwin P, Livi L. Interpreting recurrent neural networks behavior via excitable network attractors. Cognitive Computation, 2020, 12: 330-356. DOI:10.1007/s12559-019-09634-2 (  0) 0) |
| [2] |
Rivkind A, Barak O. Local dynamics in trained recurrent neural networks. Physical Review Letters, 2017, 118(25): 258101. DOI:10.1103/PhysRevLett.118.258101 (  0) 0) |
| [3] |
Farkaš I, Bosák R, Gergel P. Computational analysis of memory capacity in echo state networks. Neural Networks, 2016, 83: 109-120. DOI:10.1016/j.neunet.2016.07.012 (  0) 0) |
| [4] |
Bianchi F M, Livi L, Alippi C. Investigating echo-state networks dynamics by means of recurrence analysis. IEEE Transactions on Neural Networks and Learning Systems, 2016, 29(2): 427-439. DOI:10.1109/TNNLS.2016.2630802 (  0) 0) |
| [5] |
Gallicchio C, Micheli A, Silvestri L. Local Lyapunov exponents of deep echo state networks. Neurocomputing, 2018, 298: 34-45. DOI:10.1016/j.neucom.2017.11.073 (  0) 0) |
| [6] |
Tino P. Dynamical Systems as Temporal Feature Spaces. https://arxiv.org/pdf/1907.06382.pdf.
(  0) 0) |
| [7] |
Jaeger H. Short-Term Memory in Echo State Networks. https://www.researchgate.net/publication/247514367_Short_Term_Memory_in_Echo_State_Networks.
(  0) 0) |
| [8] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 (  0) 0) |
| [9] |
Kumar R, Srivastava S. A novel dynamic recurrent functional link neural network-based identification of nonlinear systems using Lyapunov stability analysis. Neural Computing and Applications, 2021, 33(13): 7875-7892. DOI:10.1007/s00521-020-05526-x (  0) 0) |
| [10] |
Jaeger H, Haas H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science, 2004, 304(5667): 78-80. DOI:10.1126/science.1091277 (  0) 0) |
| [11] |
Sun L L, Jin B, Yang H Y, et al. Unsupervised EEG feature extraction based on echo state network. Information Sciences, 2019, 475: 1-17. DOI:10.1016/j.ins.2018.09.057 (  0) 0) |
| [12] |
Li Z Q, Tanaka G. Multi-reservoir echo state networks with sequence resampling for nonlinear time-series prediction. Neurocomputing, 2022, 467: 115-129. DOI:10.1016/j.neucom.2021.08.122 (  0) 0) |
| [13] |
Ren F J, Dong Y D, Wang W. Emotion recognition based on physiological signals using brain asymmetry index and echo state network. Neural Computing and Applications, 2019, 31(9): 4491-4501. DOI:10.1007/s00521-018-3664-1 (  0) 0) |
| [14] |
Holzmann G, Hauser H. Echo state networks with filter neurons and a delay&sum readout. Neural Networks, 2010, 23(2): 244-256. DOI:10.1016/j.neunet.2009.07.004 (  0) 0) |
| [15] |
Deng X G, Wang S B, Jing S J, et al. Dynamic frequency-temperature characteristic modeling for quartz crystal resonator based on improved echo state network. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2022, 69(1): 438-446. DOI:10.1109/TUFFC.2021.3118929 (  0) 0) |
| [16] |
Stefenon S F, Seman L O, Neto N F S, et al. Echo state network applied for classification of medium voltage insulators. International Journal of Electrical Power & Energy Systems, 2022, 134: 107336. DOI:10.1016/j.ijepes.2021.107336 (  0) 0) |
| [17] |
Grigoryeva L, Ortega J P. Echo state networks are universal. Neural Networks, 2018, 108: 495-508. DOI:10.1016/j.neunet.2018.08.025 (  0) 0) |
| [18] |
Gallicchio C, Micheli A. Echo state property of deep reservoir computing networks. Cognitive Computation, 2017, 9: 337-350. DOI:10.1007/s12559-017-9461-9 (  0) 0) |
| [19] |
Jaeger H. The "Echo State" Approach to Analysing and Training Recurrent Neural Networks - with an Erratum Note. https://www.researchgate.net/profile/Herbert-Jaeger-2/publication/215385037_The_echo_state_approach_to_analysing_and_training_recurrent_neural_networks-with_an_erratum_note%27/links/566a003508ae62b05f027be3/The-echo-state-approach-to-analysing-and-training-recurrent-neural-networks-with-an-erratum-note.pdf.
(  0) 0) |
| [20] |
Gallicchio C, Micheli A, Pedrelli L. Deep reservoir computing: A critical experimental analysis. Neurocomputing, 2017, 268: 87-99. DOI:10.1016/j.neucom.2016.12.089 (  0) 0) |
| [21] |
Bo Y C, Wang P, Zhang X. An asynchronously deep reservoir computing for predicting chaotic time series. Applied Soft Computing, 2020, 95: 106530. DOI:10.1016/j.asoc.2020.106530 (  0) 0) |
| [22] |
Cowan N. What are the differences between long-term, short-term, and working memory?. Progress in Brain Research, 2008, 169: 323-338. (  0) 0) |
| [23] |
Inubushi M, Yoshimura K. Reservoir computing beyond memory nonlinearity trade-off. Scientific Reports, 2017, 7(1): 10199. DOI:10.1038/s41598-017-10257-6 (  0) 0) |
| [24] |
Shao W M, Tian X M. Adaptive soft sensor for quality prediction of chemical processes based on selective ensemble of local partial least squares models. Chemical Engineering Research and Design, 2015, 95: 113-132. DOI:10.1016/j.cherd.2015.01.006 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30


