2. Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology, Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin 150000, China;
3. China Energy Engineering Group Shanxi Electric Power Engineering Co., Ltd., Taiyuan 030001, China;
4. University of Maryland, Baltimore County, Maryland 21250, USA;
5. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150006, China
Wind and snow disasters occur average year in cities in cold climate regions, particularly in areas with heavy snowfall. As a result, undesirable urban planning and design typically result in a slew of negative environmental impacts in the planning space, such as a local strong wind vortex, heavy snow accumulation, and a local severe wind and snow climate[1]. Consequently, this issue adversely affects the regular use of the city's planning area and can result in material loss, traffic obstruction, restricted human behavior, and a series of other things that can compromise human safety and undermine the city's operations. Therefore, in the early stages of planning and architecture, we should focus on the prediction and research of the wind and snow environment in urban planning space, as well as the analysis of wind and snow environment inside urban planning space using accurate evaluation methods, in order to guide or optimize the technical and spatial strategies for cold regions[2-6].
Current wind and snow research methods primarily consist of field measurements, experimental methods, and numerical simulations. Initially, research was conducted using real-world measurements and wind tunnel tests. Mellor[7], for example, pioneered the study of wind and snow environments by introducing the two-phase flow theory of wind and sand motion into the study of wind and snow motion in 1965. In one study, Thiis and Gjessing[8] used three uniform height building models with different roof structures to conduct field measurements of snow distribution around building models. Oikawa[9] conducted long-term in situ observations of a cube with a 1 m side length to determine the snow distribution around the cube under various wind and snow environmental conditions. Later, Thiis[10] also investigated the distribution of snow around a large-scale building model through observation. In addition, Thiis[11] also studied snow distribution around a rectangular cube and two adjacent cube models, confirming that differences in building type design and planning space can have a significant impact on snow distribution. Tsutsumi et al.[12-13] investigated the snow distribution around a two-storey building model and a twelve-building model complex, contributing to our understanding of the wind and snow environment of buildings. Delpech[14] built a scaled-down model of the Antarctic Concordia station in the Jules Verne wind tunnel laboratory, using artificial snow to simulate the snow distribution around it.The degree of similarity between the model and the prototype was not taken into account in many early wind tunnel tests, and there were no scientific criteria for particle selection[15-17].
The most accurate measurements are made in the field, but they are subject to natural conditions, and most previous research has observed single buildings and limited areas of planning, making direct experimental tests of actual spatial layouts difficult. Additionally, wind tunnel tests are also time-consuming and expensive, which complicates testing the actual planning space model. With the advancement of computer technology in recent years, CFD technology has become an important tool for studying fluid-related engineering problems. Wind and snow simulations based on CFD techniques have advantages over actual field measurements or wind tunnel tests, such as low cost, high efficiency, time savings, intuitive and detailed calculation results, and controllable boundary conditions. Using CFD techniques, many studies have been conducted to investigate wind and snow environments. For example, Uematsu[18] pioneered the use of numerical simulation to study the wind and snow environment around a hill, and by comparing the field measurements, the numerical calculation model can efficiently predict the snow distribution around the hill. Tominaga and Mochida[19] also used numerical simulation methods to investigate the snow distribution around a nine-story building. Thiis and Ferreira[20] simulated and analyzed the distribution of snow caused by three different cube configurations, and showed that different cube layouts with different numbers of rows could result in different wind-bypassing patterns, which could potentially affect the wind and snow environment around them. Tsutsumi et al.[21] and Okaze et al.[22]used field observations and numerical simulation techniques, respectively, to study snow accumulation around 12 rectangular cubes arranged in a matrix of three rows and four columns. Zhao[23] used quartz sand as snow phase particles in a pre-lay wind tunnel test at room temperature to experimentally and simulatively study the snow distribution around three cubes in a zigzag layout. In terms of computational modelling, many new numerical computational methods were investigated to obtain snow distribution around cubic building models more efficiently and accurately[24-27]. Beyers and Waechter[28] used numerical simulations to study the snow distribution around two adjacent cubic buildings.
Despite the fact that CFD is an effective method in wind and snow engineering[27], little research has been done to simulate wind and snow environments in planning spaces. Furthermore, when the simulation results are analyzed, the wind and snow are examined separately and independently, preventing an examination of the true impact of wind and snow on the planning space.
The present paper builds on previous research using CFD technology and introduces the meteorological wind and snow index in a novel way. It attempts to analyze the wind and snow environment in the planning space using the wind speed and snow distribution from the simulation results. With a real planning space as an example, this study first used numerical calculation methods to calculate the wind and snow speed and snow distribution in the area. The meteorological wind and snow index calculation equation was then presented in order to compare the local wind and snow environment in the planning space to the rating standard. Simultaneously, this paper provides a theoretical foundation and spatial technical reference for the preliminary planning of other severe cold city construction sectors, as well as a planning and design approach for the harmonious coexistence of man and cold nature. It also refines traditional research on the external environment of buildings and provides new research ideas for related building environment research.
1 MethodologyThe wind and snow environment in the region is calculated and analyzed using a numerical simulation approach in this paper. However, in the practical application of numerical simulation, there are many factors that may directly affect the convergence and accuracy of the calculation results, and one of the important factors is the appropriate choice of turbulence model[29-30]. In this study, based on the Eulerian-Eulerian approach, we use the Eulerian multiphase flow model and the standard k-ε turbulence model to numerically simulate the wind and snow environment around the building. We also use the finite volume method and SIMPLE pressure correction algorithm to decouple and solve the non-linear discretization equations iteratively.
1.1 Theoretical Justification of Numerical Methods for Simulating Wind and Snow Environment(1) Volume fraction equation.
The volume fraction represents the total volume of all phases occupied by each phase, and each phase independently satisfies the laws of conservation of mass and momentum, where the volume of the snow phase is defined as:
| $ V_{\mathrm{s}}=\int \alpha_{\mathrm{s}} \mathrm{d} V $ | (1) |
| $ \alpha_{\mathrm{s}}+\alpha_{\mathrm{a}}=1 $ | (2) |
where αs is snow phase volume fraction; subscript s is for snow phase; αa is air phase volume fraction; subscript a is for air phase.
Effective density of the snow phase:
| $ {\widehat \rho _{\rm{s}}} = {\alpha _{\rm{s}}}{\rho _{\rm{s}}} $ | (3) |
where ρs is physical density of the snow phase, kg/m3
(2) Equation of conservation of mass.
The equation of continuity for the snow phase can be expressed as:
| $ \frac{\partial}{\partial t}\left(\alpha_{\mathrm{p}} \rho_{\mathrm{p}}\right)+\nabla \cdot\left(\alpha_{\mathrm{p}} \rho_{\mathrm{p}} \vec{v}_{\mathrm{p}}\right)=\sum\limits_{i=1}^n\left(\dot{m}_{\mathrm{ip}}-\dot{m}_{\mathrm{pi}}\right)+S_{\mathrm{p}} $ | (4) |
(3) Conservation of momentum equation.
Momentum balance equation for the snow phase can be expressed as follows:
| $ \begin{aligned} & \frac{\partial}{\partial t}\left(\alpha_{\mathrm{s}} \rho_{\mathrm{s}} \vec{v}_{\mathrm{s}}\right)+\nabla \cdot\left(\alpha_{\mathrm{s}} \rho_{\mathrm{s}} \vec{v}_{\mathrm{s}} \vec{v}_{\mathrm{s}}\right)=-\alpha_{\mathrm{s}} \nabla p+ \\ & \quad \quad \nabla \cdot \overline{\bar{\tau}}_{\mathrm{s}}+\alpha_{\mathrm{s}} \rho_{\mathrm{s}} g+\sum\limits_{i=1}^n\left(\vec{R}_{\mathrm{ip}}+\dot{m}_{\mathrm{is}} \vec{v}_{\mathrm{is}}-\dot{m}_{\mathrm{si}} \vec{v}_{\mathrm{si}}\right)+ \\ & \quad \quad\left(\vec{F}_{\mathrm{s}}+\vec{F}_{\mathrm{lift}, \mathrm{s}}+\vec{F}_{\mathrm{vm}, \mathrm{s}}\right) \end{aligned} $ | (5) |
where
The wind and snow simulations in this paper were calculated using Ansys Fluent 19.0, a commercial software for computational fluid dynamics. Table 1 shows the CFD calculation parameters and basic settings.
| Table 1 CFD calculation parameters and basic settings |
1.2 Validation of Numerical Simulation Methods for Wind and Snow Environment
(1) In this paper, using the cube as the research object, this section compares and analyses the snow distribution pattern with numerical simulation outcomes and actual measurements to demonstrate the feasibility of using the Eulerian multiphase flow model to simulate the wind and snow environment around the building.
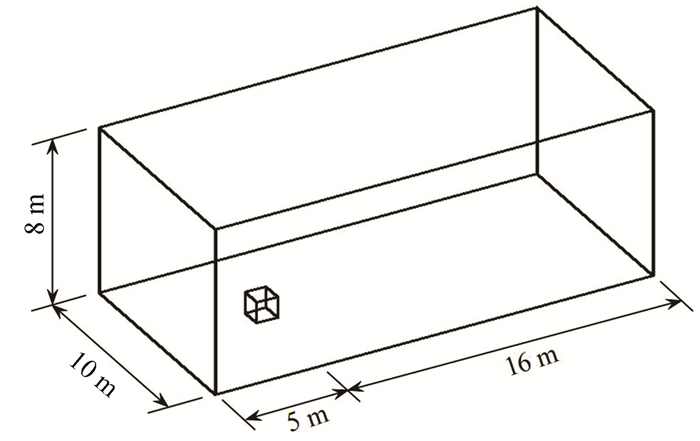
This example of validation calculation is based on a real test conducted by Oikawa[34] in 2003. The cube's side length is 1 m. The computational domain is determined by the size of the cube, as shown in Fig. 1. The entire computational domain's grid structure is a structured grid, and due to the cube model's simplicity, a minimum grid size of 0.02 m and a total number of 389340 cells were used for model validation. The grid structure division is shown in Fig. 2.
|
Fig.1 Schematic diagram of calculation model and calculation domain |

|
Fig.2 Grid structure division diagram |
In the air phase of simulation, the snow particles are treated as a continuous fluid[35] and follow the air flow when setting up the particle material. Thus, the fluid phase of simulation is the snow phase. Both the snow and air phase temperatures can be set as constants because no heat transfer process is involved in the simulation.
(2) Validation analysis of calculation results.
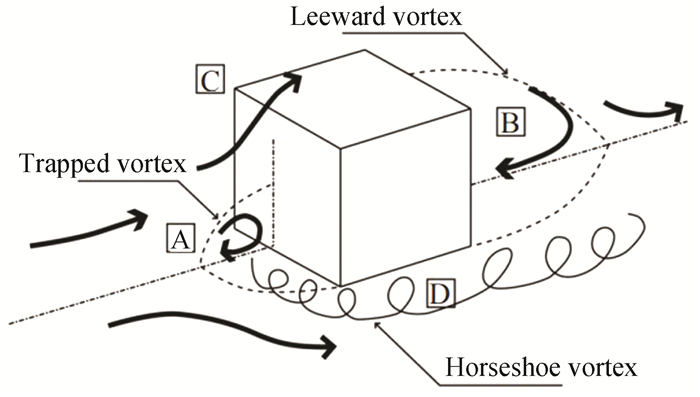
For the discrete equation set's pressure-velocity method, SIMPLE pressure correction is used, with a Body Force Weighted pressure term. The parameters used in second-order windward differential format are momentum, turbulent kinetic energy, and turbulent dissipation rate. The flow in the computational domain takes gravity into account, with the gravitational acceleration in the z-axis direction set to -9.81 m/s2 and the simulated snowfall time set to 60 min. The simulation results were post-processed using Tecplot with CFD-post, as shown in Fig. 3, to obtain top and side views of the flow and pressure in the windward section of the cube, which was consistent with the wind and snow flow field around the cube as simplified in the study[36]. Two-phase flow is used in the numerical simulation of wind and snow movement. In the wind snow two-phase flow, wind and snow are regarded as two-phase or multiphase mixed fluid. The air phase is the main phase. In the wind snow flow, the volume fraction of snow particles is very small, as is the size of snow particles. A dilute phase homogeneous flow model can be used to simulate wind and snow two-phase flow in an urban wind environment, ignoring the hysteresis of snowflakes in the airflow, and the wind and snow two-phase flow is considered as a proposed single-phase flow. The simplified flow field diagram of wind and snow flow around the cube is shown in Fig. 4.

|
Fig.3 Flow diagram of windward section of cube |
|
Fig.4 Simplified flow field diagram of wind and snow flow around the cube(From Ref.[34], reprinted with permission from the authors licensed under CC-BY4.0) |
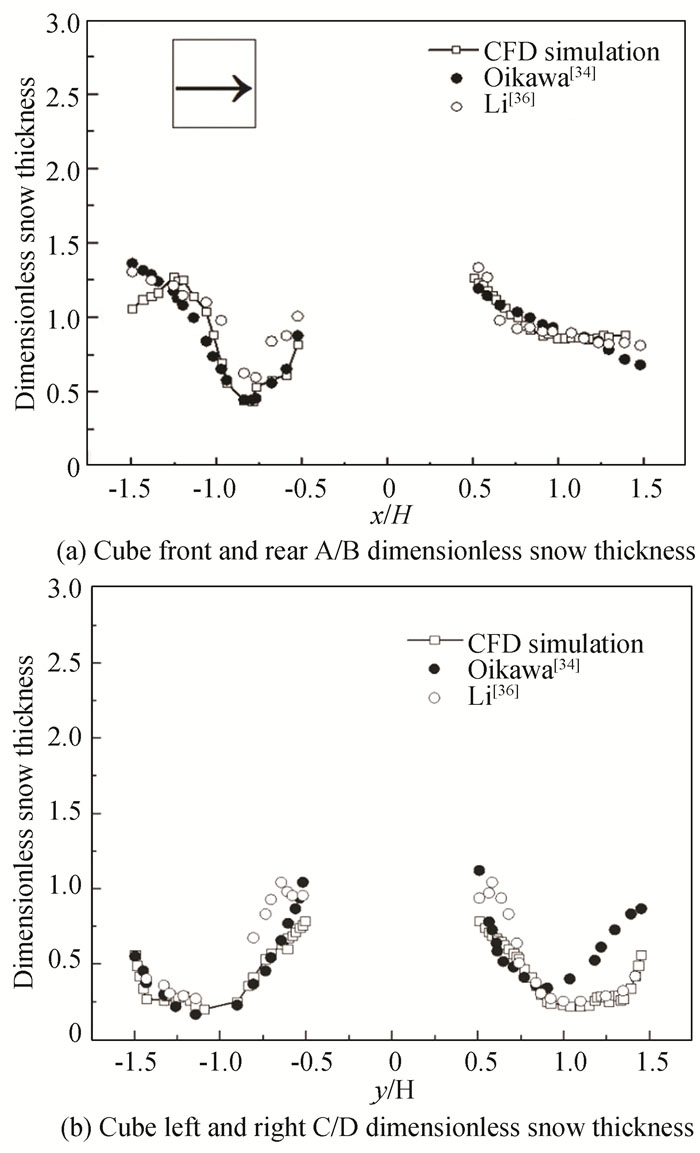
As shown in Fig. 5, the numerical simulation of the snow distribution pattern in the downwind direction closely matches the experimental results, indicating that the Eulerian multiphase flow numerical simulation method used above has a high reliability; however, there is some asymmetry in the measured values in the b-plot. This discrepancy could be resulted from the fact that previous research has not provided a clear incoming wind direction, but the margin of error is quite small. As a result, the method can be applied to future numerical simulation studies of wind and snow flows.
|
Fig.5 Comparison of simulation results with measured values |
2 Evaluation Criteria for Wind and Snow Environments
After confirming the applicability of this numerical method, the above simulation method can be used to obtain the wind and snow velocity and snow distribution in the region. This paper introduces the meteorological wind and snow level standard in an innovative way, using the meteorological wind and snow level calculation equation to simulate the wind and snow impacts in urban planning regions. Using the speed and snow distribution data, the wind and snow index can be obtained, which is comprehensive in its application as wind and snow environment evaluation criteria, based on the level requirements to evaluate wind and snow environment in the region on life, production, traffic, and other impacts, scientific and effective to make an evaluation of the wind and snow environment in the region, and to provide a reference basis for early planning and design.
The storm weather grade criteria are introduced in the snow and wind environment evaluation. This criterion, according to the specification, applies to all urban areas where wind and snow disasters are possible and is primarily used to describe the severity of wind and snow weather[37]. The area chosen for the following section of this paper is also on the mesoscale scale. Therefore, this method is used to simulate the regional wind and snow environments shown below, and this scale can be applied as long as fine wind and snow velocity and snow distribution are obtained. The SWI (snowstorm weather index), which is the wind and snow index, is usually used to calculate the SWG (snowstorm weather grade).
Three meteorological factors, namely snowfall, maximum wind speed, and minimum visibility, are chosen as influencing factors for the snowstorm weather index (SWI). First, for a specific point in the region, the maximum wind speed is its speed. Aside from that, the dimensionless snow thickness used in this paper refers to the ratio of snow distribution at a given point to the average snow distribution. Because the average simulated snowfall thickness is 1 mm, snow thickness at a specific point is dimensionless snow thickness. As a result, the meaning of the factors can be aligned, as can the SWG standard.
To accurately describe the micro-scale regional snow and wind environment, snowfall is chosen as the snow thickness, maximum wind speed is chosen as the fixed point wind and snow speed in the region, and minimum visibility is taken as the maximum value of 1.0.
Snowstorm Weather Index (SWI) was calculated as shown in Eq.(6):
| $ \begin{aligned} S_{\mathrm{WI}}= & 0.58 \times(R / 2.5)+0.59 \times(W / 13.9)+ \\ & 0.79 \times V_{\mathrm{IS}} \end{aligned} $ | (6) |
where SWI is snowstorm Weather Index; R is calculated dimensionless snow thickness, R=αs/αs(average); W is the calculated wind and snow mixing speed, m/s; The component in the x direction is denoted by i; The component in the y direction is denoted by j; The component in the z direction is denoted by k; vi is the component of wind and snow mixing speed in x direction, which is calculated as vi=(via+vis)/2 m/s.vj is the component of wind and snow mixing speed in y direction, which is calculated as vj=(vja+vjs)/2 m/s.vk is the component of wind and snow mixing speed in z direction, which is calculated as vk=(vka+vks)/2 m/s; The letter a represents the air phase, while the letter s represents the snow phase; VIS is minimum visibility, km, VIS selected for 1 in this text.
Storm Weather Grade is classified into four categories, as shown in Table 2 and 3: Light Storm Weather, Moderate Storm Weather, Strong Storm Weather and Very Strong Storm Weather. Table 2 displays the various SWI and SWG values associated with various meteorological parameters.
| Table 2 SWG with various meteorological parameters |
| Table 3 SWG classification |
Based on the rating criteria[37], the impact of the wind and snow environment can be further evaluated, including the degree of impact of the wind and snow environment on traffic, residents' outdoor activities, etc., and can be used as a general guideline for avoiding the risks caused by the wind and snow environment, as shown in Table 3.
3 Case Study of Planning Space Wind and Snow Environment Model 3.1 Case IntroductionIn this paper, Harbin (45° 450N, 126° 400E) is chosen as the representative city in the severe cold area. Harbin is located in a harshly cold region of northeast China. The cold area chosen for this paper is a planned region in Harbin.
The long-term meteorological data of Harbin is statistically analyzed using the meteorological data of Harbin from January 1994 to December 2013 obtained from the NOAA open-source database Integrated Surface Data of the National Oceanic and Atmospheric Administration of the United States.
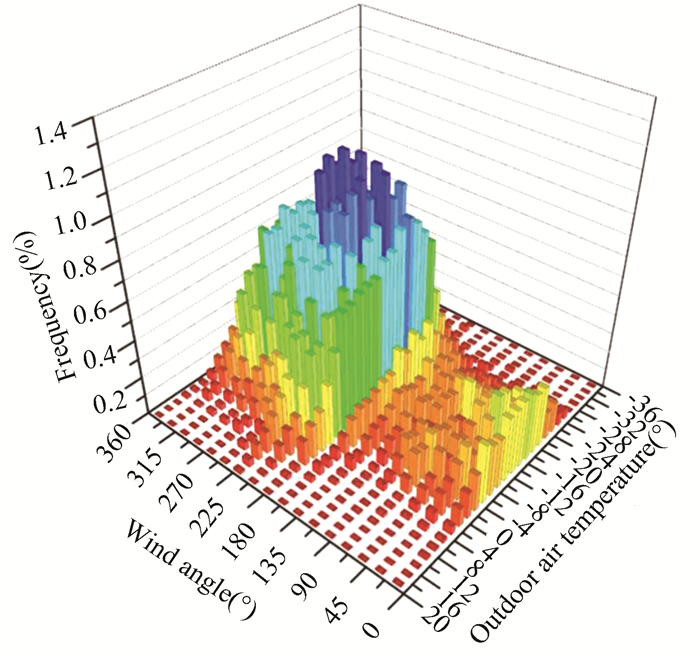
Fig. 6 depicts the joint distribution of wind direction and temperature in Harbin in winter[38]. The overall winter air temperature in Harbin is low, as shown by the graph. To be exact, in terms of wind direction, cold air below -20℃ is most likely to come from the south (wind angle 180°) and southwest (wind angle 225°) with a probability of 3.77%.
|
Fig.6 Joint distribution of wind direction and air temperature in winter for Harbin(From Ref.[39], reprinted with permission from the authors licensed) |
Fig. 7 shows the wind rose diagram of annual and seasonal wind speed and direction distribution based on long-term meteorological data statistics of Harbin. Each season is divided according to the definition of perennial climate seasons in the meteorological industry standard "Division of Climate Seasons" (QXT 152-2012). The figure shows that the dominant wind direction in Harbin throughout the year is southwest wind, with a wind frequency of 12.28% and an average wind speed of 3.18 m/s; the dominant wind direction in winter is also southwest wind, with a wind frequency of 12.39% and an average wind speed of 2.91 m/s.
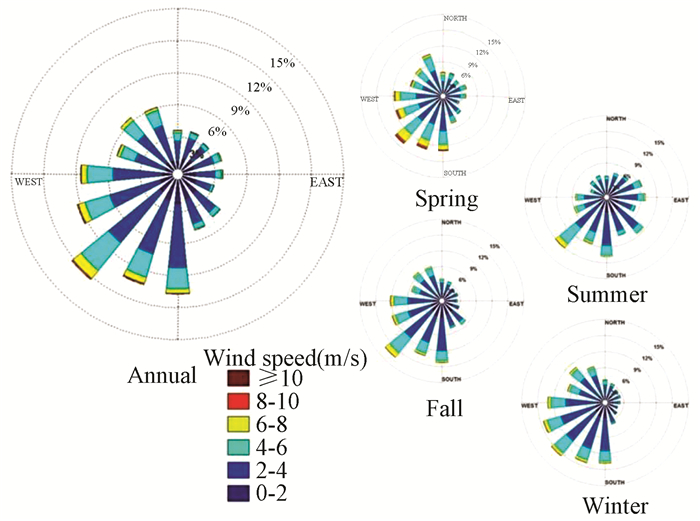
|
Fig.7 Annual and seasonal wind roses for Harbin(From Ref.[39], reprinted with permission from the authors licensed) |
This paper examined a typical wind and snow environment for a Harbin urban area planning base map. As shown in Fig. 8, the area was modelled in Sketch up. According to the research, the area has a dense concentration of small hills upstream of the dominant winter wind direction, which is depicted in the figure as the pink area. We kept the hills to ensure the case's authenticity, but their height is only 3 m and they are far from the buildings. The effect of the hills on the wind and snow flow field can be ignored when compared to the height of the buildings. Furthermore, the prevailing wind direction is south-west, and after adjusting the model direction, the wind in Fig. 8 blows from left to right, corresponding to the actual south-westerly wind. The complex is made up of a mixed arrangement of 18 buildings of varying heights; the individual buildings in the area are designed to standardize the modular treatment, and the complex layout is preserved in its current form.
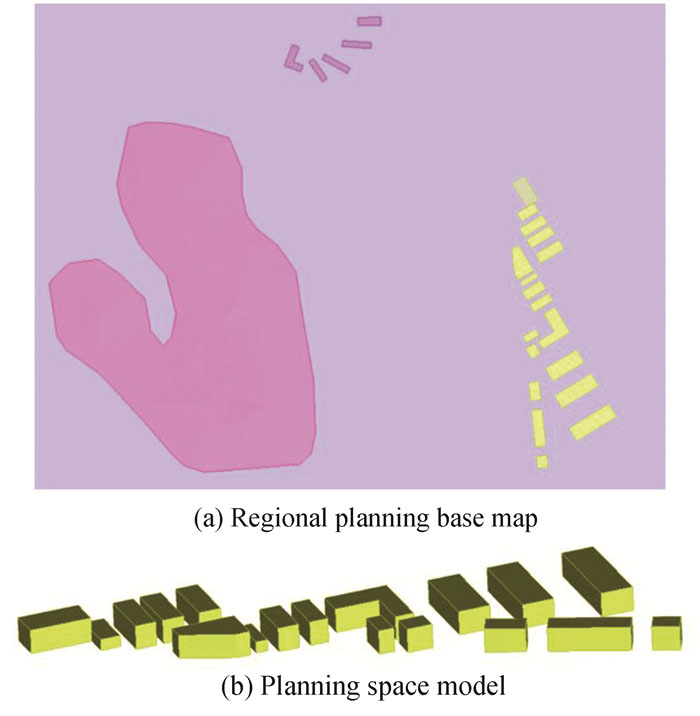
|
Fig.8 Actual planning model |
In addition, the geometric model was meshed using ANSYS (ICEM). The whole computing domain adopts unstructured grid for spatial discretization. Near the ground, the boundary layer grid was used, and the grids were then arranged non-uniformly and locally encrypted near the building walls. ICEM is used to calibrate the grid quality measurement index. For different types of grids, different measurement methods were used. For triangle or tetrahedron grids used in this paper, the height to length ratio of each side was calculated, and the smallest value was used. The closer the grid quality is to 1, the better. The ICEM grid quality inspection yielded a minimum value of 0.75, a maximum value of 1, and an average value of around 0.9. The places with poor grid quality were concentrated in the hills, and the grid was also repaired automatically. Because of the height of the hills and the distance between the buildings, the quality of the hills was thought to have no effect on the basic buildings. The dimensionless distance y+ was about 180; the smallest grid size along the height direction was 0.5 m.
The number of grids has a significant impact on the accuracy of simulation results. It is necessary to obtain the appropriate number of grids that can not only ensure calculation accuracy, but also reduce calculation time through grid independence test. According to Ferziger et al.[40], the number of fine grids in each dimension should be at least 1.5 times that of rough grids in grid independence test. Based on this principle, the case is divided into three grids of varying precision: rough grid, basic grid and fine grid. The grid diagram of three types of precision is shown in Fig. 9, with a total of 2712620 basic grids, 904240 coarse grids, and 3630460 fine grids.

|
Fig.9 Perspective view of grids with different cells for grid-sensitivity analysis |
Fig. 10 compares SWI results at 12 measuring points obtained from the three precision grid simulations. It can be seen from the figure that the simulation results of the basic grid and the fine grid are basically consistent, whereas the simulation results of the rough grid and the basic grid are significantly different, indicating that the basic grid ensures the simulation accuracy while reducing the number of grids compared with the fine grid, resulting in less calculation and calculation time. Therefore, the grid parameters of the basic grid division are used for the grid division of each working condition in this paper.

|
Fig.10 The grid-sensitivity analysis results |
3.2 Analysis of Results
Here, the simulation results were compared and analyzed in terms of wind and snow velocity, snow distribution, and wind and snow environment level. The case study complex consists of 18 buildings of varying heights arranged in a complex pattern. Fig. 11 depicts the wind and snow velocity clouds at 1.5 m pedestrian height in the horizontal plane, Fig. 12 depicts the snow distribution at ground level.
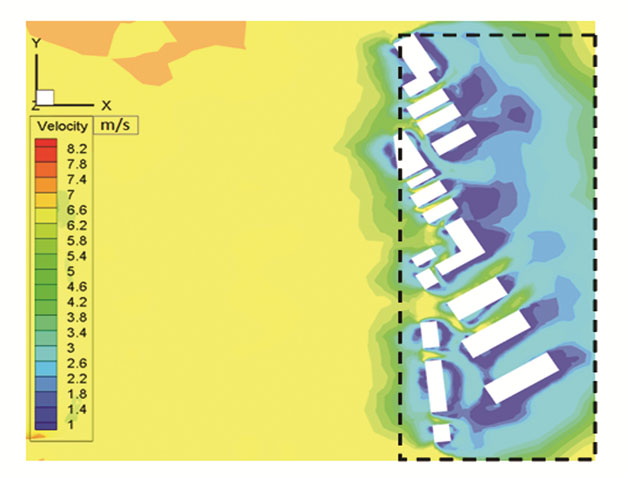
|
Fig.11 Wind and snow speed (m/s) |
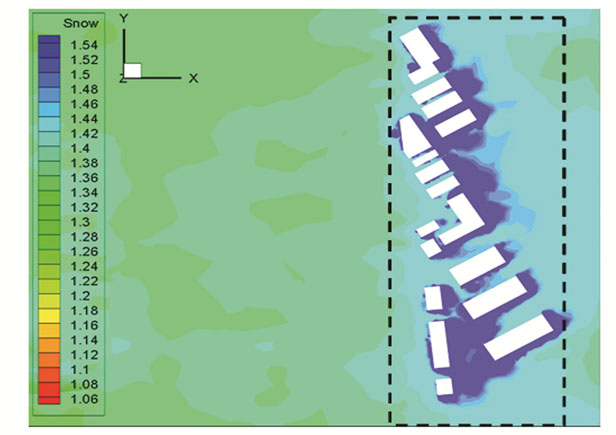
|
Fig.12 Snow distribution at ground level |
(1) Calculation results for wind and snow speed and snow distribution
As the incoming wind and snow flow velocity increases upstream to 6.5 m/s, residents' mobility in this area will be impeded and people will be more likely to feel uncomfortable due to the impact of snow particles on the human body, as shown in Fig. 11. While flowing through the building complex, the velocity is reduced due to the building complex's blocking effect, and the average height of the building complex is low, so the downwash velocity is smaller, and only a small area within the building complex has a velocity greater than 6 m/s. As a result, wind and snow velocities are not critical factors in influencing people's outdoor activities within this area. However, as shown in Fig. 12, it is clear that in the leeward areas of each building, a vortex is formed, and within the vortex, velocities are low and snow accumulation is likely, so snow distribution will be a key factor influencing people outside; whereas within the windward street valley, the velocity of the mixed flow increases due to the canyon effect, so erosion and accumulation are less likely.
(2) Wind and snow environment grade
The distribution of wind and snow levels enables a visual analysis of the combined effect of wind and snow on the external environment of the building. As shown in Fig. 13, the blue area in this building complex has a SWI index of less than 1.6, indicating a mild blizzard rating area that may cause traffic congestion, traffic accidents, and interfere with people's normal outdoor activities. There are green and yellow areas near some buildings with SWI indices between 1.6 and 2.5, occasionally greater than 3, indicating a moderate snowstorm level.However, as the scope of these areas is small, the impact on transportation is not significant. Meanwhile, local power lines and communication lines will be disrupted, which will seriously affect people's normal activities, so it is not recommended to install these facilities outside.Furthermore, as shown in Fig. 13, these areas are primarily in high snow areas, where snow distribution has a greater impact on the wind and snow environment.
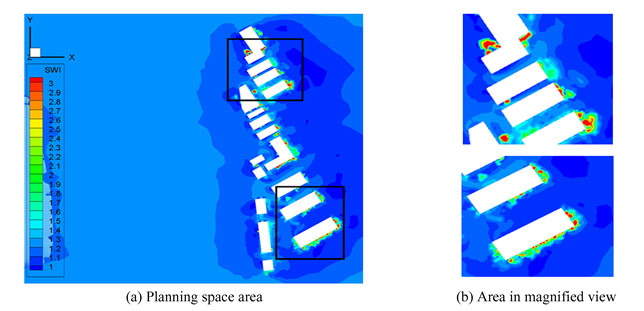
|
Fig.13 Wind and snow environment grade cloud map |
As shown in Fig. 14, 150 measurement points were chosen in the planning space. In Fig. 15, 150 measurement points are shown using the two dimensions of wind and snow velocity and snow distribution, but no correlation between the wind and snow environment can be drawn, nor can the wind and snow environment at that measurement point be specifically judged.
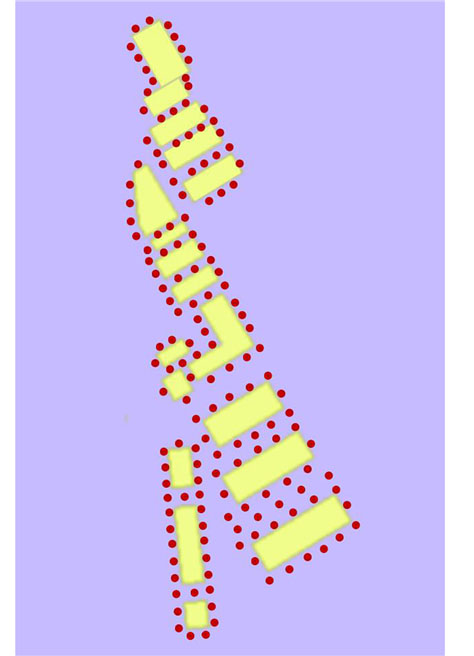
|
Fig.14 Measurement points |

|
Fig.15 Velocity and snow at measurement points |
The wind and snow environment of this planning space, however, can be expressed as an SWI index by combining the results of wind and snow environment calculations from 150 measurement points, as shown in Fig. 16. Using the original calculation equation and the average snowfall and wind speed for the entire area, the solid orange line depicts the average calculation result. This area's SWI index is 1.38, indicating a mild wind and snow grade that may cause traffic congestion and frequent traffic accidents, as well as affecting residents' outdoor activities. However, the SWI clearly exceeds 1.38 at all points near buildings. The solid black line represents the moderate wind and snow grade, while the dotted black line represents the strong wind and snow grade. As shown in Fig. 15 and Fig. 16, 55% of the points are in the moderate wind and snow category, indicating that transportation in the area may be disrupted, affecting the normal operation of power and communication lines and seriously affecting residents' outdoor activities. Furthermore, 1.3% of the points are in the category of strong wind and snow. Since the range is relatively small, the impact is still in the category of moderate wind and snow.

|
Fig.16 SWI distribution at measurement points |
The average value of the entire region was previously used to evaluate the wind and snow environment in the planning space, but this approach frequently resulted in large margins of error, and the evaluation of the wind and snow environment in the region was inaccurate. Our research method, on the other hand, combines the results of the wind and snow environments, allowing for accurate evaluation of specific areas or locations.
4 ConclusionsFirst, the Eulerian multiphase flow method was used to study the wind and snow environment around the cube, which was then validated with experimental results, demonstrating that the Eulerian multiphase flow model is highly reliable for the simulation of wind and snow environments in planning space. Second, in this paper, an actual urban planning space design was chosen and modelled. The Eulerian multiphase flow numerical simulation method was used to obtain the calculation results of wind and snow velocity and snow distribution in this planning space, and the wind and snow index was incorporated to obtain the wind and snow environment level distribution. The following conclusions have been reached:
(1) The SWI index is a useful tool for digitally displaying the combined effect of wind and snow environments, as well as visually describing the impact of wind and snow environments on life, transportation, and facilities in relation to wind and snow class norms.
(2) In this paper, 150 measurement points were chosen, with 55% falling into the moderate wind and snow category and 1.3% falling into the intense wind and snow category. This paper was able to realize the evaluation of the wind and snow environment in the fixed-point area while effectively avoiding the error introduced by the average SWI index evaluation across the entire planning space.
(3) It is demonstrated in our paper that by combining the numerical simulation calculation method with the wind and snow environment evaluation method, the comfort and safety of the wind and snow environment in a specific area can be evaluated intuitively and quantitatively, allowing future urban planning to have a more accurate understanding of the wind and snow environment around the building complex.
Our approach provides a powerful tool for climate-based planning and design, as well as well-informed recommendations for cold urban planning and design. The study of the wind and snow environment in the planning space is critical for the life, production, and traffic in the planning space. The evaluation of the wind and snow environment in the planning space can be realized based on the research in this paper, so that the damage caused by the wind and snow environment can be effectively avoided. However, there are some limitations in this paper that will be the focus of our future research:
(1) Considering wind and snow movement is a complex flow phenomenon, future models should include the pushing or rolling of snow as it occurs on the ground when wind and snow are simulated.
(2) A better correlation between outdoor comfort and wind and snow conditions needs to be achieved through more research using machine learning methods to match wind and snow conditions with outdoor comfort.
AcknowledgmentsThe authors are grateful to the members of the Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology, Ministry of Industry and Information Technology in Harbin Institute of Technology, for providing invaluable information and advice in this study.
| [1] |
Li Y, Chen L. Study on the influence of voids on high-rise building on the wind environment. Building Simulation, 2020, 13(2): 419-438. DOI:10.1007/s12273-019-0584-7 (  0) 0) |
| [2] |
Norman Pressman. Reshaping Winter Cities: Concepts, Strategies and Trends. Ontario: University of Waterloo Press, 1985.
(  0) 0) |
| [3] |
Regional/Urban Design Assistance Team Program, Royal Architectural Institute of Canada. Livable Winter Cities. Edmonton, Alta. : Regional/Urban Design Assistance Team, 1986.
(  0) 0) |
| [4] |
Winter Cities '86 Corporation, Edmonton (Alta. ), Livable Winter City Association. Winter Cities Forum '86: Symposium Proceedings: Finding a Cure for the Common Cold. Edmonton, 1986.
(  0) 0) |
| [5] |
Jorma Mänty, Norman Pressman. Cities Designed for Winter. Helsinki: Building Book Ltd, 1988.
(  0) 0) |
| [6] |
Norman Pressman. Institute of Urban Studies, Images of the North: Culture Interpretations of Winter. Winnipeg, Canada Institute of Urban Studies, 1988.
(  0) 0) |
| [7] |
Mellor Malcolm. Cold Regions Science and Engineering, Part Ⅲ, Section A3c: Blowing snow. Hanover, New Hampshire: U.S. Army Materiel Command Cold Regions Research and Engineering Laboratory, 1965: 1-81.
(  0) 0) |
| [8] |
Thiis T K, Gjessing Y. Large-scale measurements of snowdrifts around flat-roofed and single-pitch-roofed buildings. Cold Regions Science and Technology, 1999, 30(1-3): 175-181. DOI:10.1016/S0165-232X(99)00021-X (  0) 0) |
| [9] |
Oikawa S, Tomabechi T, Ishihara T. One-day observations of snowdrifts around a model cube. Journal of Snow Engineering of Japan, 1999, 15(4): 283-291. DOI:10.4106/JSSE.15.4_283 (  0) 0) |
| [10] |
Thiis T K. Large scale studies of development of snowdrifts around buildings. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(6): 829-839. DOI:10.1016/S0167-6105(02)00474-9 (  0) 0) |
| [11] |
Thiis T K, Jaedicke C. The snowdrift pattern around two cubical obstacles with varying distance-measurements and numerical simulations. Proceedings of the 4th International Conference on Snow Engineering. Trondheim, Norway, 2000. 369-375.
(  0) 0) |
| [12] |
Tsutsumi T, Tomabechi T, Chiba T. Field measurement of snowdrift around a building using full-scale model. Summaries of JSSI & JSSE Joint Conference on Snow and Ice Research, 2010, 26(4): 184-185. DOI:10.14851/jcsir.2009.0.184.0 (  0) 0) |
| [13] |
Tsutsumi T. Snowdrifts on and around buildings based on field measurement. Proceedings of the 7th International Conference of Snow Engineering. Fukui, Japan: Snow Engineering Ⅶ Organizing Committee, 2012.9-17.
(  0) 0) |
| [14] |
Delpech P, Palier P, Gandemer J. Snowdrifting simulation around Antarctic buildings. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 567-576. DOI:10.1016/S0167-6105(98)00051-8 (  0) 0) |
| [15] |
Nokkentved C. Investigation on snow fences. Stads-og havneingeniøren, 1938, 30(8): 111-114. (  0) 0) |
| [16] |
Finney E A. Snow drift control by highway design results of wind tunnel investigations interpreted. Roads Streets, 1940, 83(3): 45-48. (  0) 0) |
| [17] |
Becker A. Natural snow fences along roads. Bautechnik, 1944, 22: 161-166. (  0) 0) |
| [18] |
Uematsu T, Nakata T, Takeuchi K, et al. Three-dimensional numerical simulation of snowdrift. Cold Regions Science and Technology, 1991, 20(1): 65-73. DOI:10.1016/0165-232X(91)90057-N (  0) 0) |
| [19] |
Tominaga Y, Mochida A. CFD prediction of flowfield and snowdrift around a building complex in a snowy region. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 81(1-13): 273-282. DOI:10.1016/S0167-6105(99)00023-9 (  0) 0) |
| [20] |
Thiis T, Ferreira Almerindo D. Sheltering effect and snow deposition in arrays of vertical pillars. Environmental Fluid Mechanics, 2015, 15(1): 27-39. DOI:10.1007/s10652-014-9356-1 (  0) 0) |
| [21] |
Tsutsumi T, Chiba T, Tomabechi T. Snowdrifts on and around buildings based on field measurement. Proceedings of the 7th International Conference on Snow Engineering. Fukui, 2012. 9-17.
(  0) 0) |
| [22] |
Okaze T, Kato S, Tominaga Y, et al. CFD prediction of snowdrift in a building array. Proceedings of the 8th International Conference on Snow Engineering. Nantes, 2016. 26-29.
(  0) 0) |
| [23] |
Zhao L. Study on Snowdrift on Low-rise Buildings Through Field Measurement, Wind Tunnel Test and Numerical Simulation. Chengdu: Southwest Jiaotong University, 2017.
(  0) 0) |
| [24] |
Beyers J H M, Sundsbo P A, Harms T M. Numerical simulation of three-dimensional transient snow drifting around a cube. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(9): 725-747. DOI:10.1016/j.jweia.2004.03.011 (  0) 0) |
| [25] |
Tominaga Y, Okaze T, Mochida A. CFD modeling of snowdrift around a building: An overview of models and evalution of a new approach. Building and Environment, 2011, 46(4): 899-910. DOI:10.1016/j.buildenv.2010.10.020 (  0) 0) |
| [26] |
Sun Xiao-Ying, Hong Cai-Bin, Wu Yue, et al. Numerical simulation of snow drifting around building model. Engineering Mechanics, 2014, 31(4): 141-146. DOI:10.6052/j.issn.1000-4750.2012.11.0839 (  0) 0) |
| [27] |
Liu Mengmeng, Zhang Qingwen, Fan Feng, et al. Experiments on natural snow distribution around simplified building models based on open air snow-wind combined experimental facility. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 173: 1-13. DOI:10.1016/j.jweia.2017.12.010 (  0) 0) |
| [28] |
Beyers M, Waechter B. Modeling transient snowdrift development around complex three-dimensional structures. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10-11): 1603-1615. DOI:10.1016/j.jweia.2008.02.032 (  0) 0) |
| [29] |
Wright N G, Easom G J. Development and validation of a non-linear k-ε model for flow over a full-scale building. Wind and Structures, 2001, 4(3): 177-196. DOI:10.12989/WAS.2001.4.3.177 (  0) 0) |
| [30] |
Jin Xin-Yang, Yang Wei, Jin Hai, et al. Comparative study of turbulence model on prediction of wind pressure and wind velocity around rectangular buildings. Building Science, 2006, 22(5): 1-5. (  0) 0) |
| [31] |
Syamlal M. The Particle-particle Drag Term in a Multiparticle Model of Fluidization. Springfield: National Technical Information Service, 1987.
(  0) 0) |
| [32] |
Schaeffer David G. Instability in the evolution equations describing incompressible granular flow. Journal of Differential Equations, 1987, 66(1): 19-50. DOI:10.1016/0022-0396(87)90038-6 (  0) 0) |
| [33] |
Lun C K K, Savage S B, Jeffrey D J, et al. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. Journal of Fluid Mechanics, 1984, 140: 223-256. DOI:10.1017/S0022112084000586.am (  0) 0) |
| [34] |
Oikawa S, Tomabechi T. Formation processes of the deposition and erosion of snow around a model building. Seppyo, 2003, 65(3): 207-218. DOI:10.5331/SEPPYO.65.207 (  0) 0) |
| [35] |
Bintanja R. Snowdrift suspension and atmospheric turbulence. Part Ⅰ: Theoretical background and model description. Springer Netherlands, 2000, 95: 343-368. (  0) 0) |
| [36] |
Li Xuefeng. Research on Snow Drifting on Building Roof and Around Building. Shanghai: Tongji University, 2011.
(  0) 0) |
| [37] |
Standardization Administration of China. Classification of Snowstorms(GB/T 34298-2017). Beijing: Standardization Administration of China, 2017.1-3.
(  0) 0) |
| [38] |
China Meteorological Administration. Classification of Climatic Seasons (QX/T 152-2012). Beijing: Meteorological Publishing House, 2012.
(  0) 0) |
| [39] |
Shui Taotao. Prediction and Evaluation of Wind and Thermal Environment of Urban Residential Areas in Severe Cold Regions. Harbin: Harbin Institute of Technology, 2018.
(  0) 0) |
| [40] |
Ferziger J H, Peric M. Computational Methods for Fluid Dynamics (3rd edition). Berlin: Springer, 2002.
(  0) 0) |
 2023, Vol. 30
2023, Vol. 30



