In recent years, the Chinese high-speed railway industry has developed rapidly and the number of EMU trains has increased. Maintenance of EMU trains has become a major concern for researchers. During actual operation, EMU trains are affected by environmental factors, especially on lines with extreme environments such as the Lanzhou-Xinjiang line. At the same time, each EMU train is a complex multi-component system internally. There are also various correlations between the components. Therefore, the maintenance decision of EMU trains faces great challenges.
The special natural environment makes it necessary to consider the influence of several environmental factors when making maintenance decisions for EMU trains. Under the influence of extreme environments such as sand and extreme temperature, the reliability evolution of EMU trains will change significantly[1-2]. Ref.[3] tracked statistics on the maintenance work such as wheel wear cycle, gate inspection cycle, and hook cleaning cycle of CRH5G model train on the Lanzhou-Xinjiang line. The research also provided corresponding maintenance improvement suggestions under the natural environment of the Lanzhou-Xinjiang line. Han et al.[4] made a statistical analysis of the aging of rubber components such as air springs and door seals in the sandy and extreme temperature environment between day and night.
The influence of external environment on the reliability of EMU components can be divided into two categories: 1) Environmental factors can be considered as the operating conditions of the components[5]. Extreme temperature has a negative effect on the wear life of rubber components and brake pads; 2) The other category of environmental factors can be considered as the random impact on components. Strong wind and sand can greatly affect the performance of lubricating grease of vibration-damping components and transmission components, making the components fail faster. Many scholars have conducted studies on the influence of operating conditions on maintenance models[6]. Xia et al.[7] introduced environmental impact factors to quantify the influence of environmental conditions on the evolution of failure rate. The paper proposed a non-perfect failure rate evolution model considering changes in environmental conditions for the maintenance of port equipment. You et al. [8] took the equipment processing load as a covariate, and conducted tests on the sequential loading of different operating conditions sequence. Finally, a non-perfect maintenance model for equipment under dynamic loading was constructed by combining the proportional failure model and the non-perfect maintenance approach. Hu[9] focused on the Markov process of the system under the influence of time-varying environment, in which the transfer matrix of the deterioration state changes with the environmental changes. The average maintenance cost is reduced by the proposed joint strategy of inspection and maintenance. Another environmental factor strongly affects component reliability in the form of stochastic shocks[10].Eryilmaz et al. [11] proposed a hybrid shock model that divides external shocks into extreme shock and run shock. Yang et al.[12] further modeled the failure rate under the influence of internal recession and external shocks, and refined the internal failure process into normal and defective stages. The study optimized the preventive replacement cycle T, inspection cycle s and inspection number m of the equipment.
The multi-component system in the EMU train is complex which consists of machine, electrical and hydraulic components. According to Thomas[13], the correlations considered in the maintenance models of multi-part systems are usually classified into three types: economic correlations, fault correlations, and structural correlations. Currently, two main types of maintenance strategies on multi-component systems exist, i.e., group maintenance and opportunistic maintenance strategies[14]. Wang et al.[15] modeled the complex correlations of components in the system by fault chains and proposed a grouping maintenance strategy, which was optimized by genetic algorithms. Vu et al.[16] proposed a dynamic grouping model with rolling time axis and considered the effect of repair time of preventive maintenance and replacement on grouping modeling and grouping optimization, as well as the economic correlations between components. Bouvard et al. [17] applied a dynamic planning model to find the best balance point within the maintenance adjustment range to minimize the maintenance adjustment cost. Do et al. [18] proposed a dynamic grouping maintenance strategy based on the positive economic correlations by considering the preventive maintenance time and the planned range, and optimized the dynamic grouping based on the rolling range.
In conclusion, some literature addressed the influence of environmental factors on the reliability of EMU trains. When the reliability evolution pattern changes, the maintenance costs of EMU trains would alter under its influence. Some literature focuses on correlation factors in multi-component systems, for which different correlations require different adjustments in maintenance strategies. The current research provides little analysis and study for the maintenance decision problem of EMU trains under the joint effect of environmental influence and correlations. In fact, the influence of multiple factors makes the problem more complex to solve. In this paper, the focus is on EMU train system and a comprehensive maintenance model is proposed for EMU trains considering the joint effect of environmental influence and correlations. Finally, the maintenance decision is optimized by a new dynamic maintenance strategy.
The rest of the paper is organized as follows: Section 1 defines the research subjects. In Section 2, the maintenance model is established with the analysis of failure rate and costs. Section 3 presents the dynamic maintenance strategy and its process in detail. In Section 4, a numerical example analysis is provided. Finally, Section 5 concludes the paper and provides directions for future research.
1 Structure of EMU Train SystemAn EMU train consists of 8 carriages, 4 of which are power carriages and the other 4 are non-power carriages. Each power carriage has two power bogies, and each non-power carriage has two non-power bogies. The bogie system is an important part of EMU trains, and the number of failures of the bogie system accounts for about 21% of the total failures[19]. Considering the maintenance difficulty and maintenance frequency of bogies, we assume bogie systems form the EMU train in series, as shown in Fig. 1. It is assumed that the EMU train shuts down when one component of the bogie is under preventive maintenance, and maintenance is performed for the same type of components in all bogies. Each bogie is considered as a multi-unit system. There are two types of multi-unit systems because the structure of power bogies and non-power bogies are different.

|
Fig.1 EMU train system |
2 Model Descriptions
In this paper, an EMU train composed of bogie system in series is studied. The objective is to optimize the maintenance decision on the mileage interval [0, Lmax] to reduce the maintenance costs. Economic correlations and fault correlations are considered. The assumptions are as follows.
(1) The initial failure rate of each component follows two-parameter Weibull distribution. The failure rate of components is influenced by environmental factors.
(2) There are mainly two types of maintenance actions: minimal repair and preventive maintenance. Preventive maintenance restores the component as good as new with the EMU train shutdown; minimal repair is implemented without shutdown after the failure and the reliability of the component would not change.
(3) Preventive maintenance generates downtime costs. Preventive maintenance of components can be carried out together to reduce the total cost. It reveals the economic correlations between components.
(4) Within a bogie system, the failure rate of one component affects that of other components by accelerating the deterioration process. Therefore, there are fault correlations between components[20-21].
2.1 Failure Rate and Reliability ModellingAccording to the assumptions, component i belongs to either power bogie or non-power bogie. Vp is the component set of power bogie and Vnp is the component set of non-power bogie. The initial failure rate follows two-parameter Weibull distribution. The initial failure rate of component i is given:
| $ \lambda_i^0(l)=\frac{\alpha_i}{\beta_i}\left(\frac{l}{\beta_i}\right)^{\alpha_i-1} $ | (1) |
where αi and βi denote the shape and dimensional parameters of component i, respectively. We assume the mileage in a year is Ly. Ref.[4] shows that the sand blown and extreme temperatures have great impacts on the reliability of components of EMU trains. With seasonal changes of environment, the mileage in a year can be divided into θ interval segments:
| $ \left[0, L_y\right]=\left[l_1, l_2\right] \cup\left[l_2, l_3\right] \cup \ldots \cup\left[l_\theta, l_{\theta+1}\right] $ | (2) |
Each interval k corresponds to a specific environmental factor εk. The total length of the mileage is assumed to be Lmax and Lmax>Ly. It is important to identify the year and the interval of mileage when calculating the failure rate. If the current mileage is l, let ld=lmodLy,
| $ \lambda_i^I(l)=\varepsilon_k \lambda_i^0\left(\varepsilon_k\left(l_d-l_k\right)+\sum\limits_{j=1}^{k-1} l_{\text {eq }}^j+l_s L_{\text {eqy }}\right) $ | (3) |
According to the study of component failure correlations in Ref.[20], the influence of component j on the failure rate of component i can be expressed by the correlation coefficient γij. The failure correlation coefficients between power bogie components form the matrix A(1), and the failure correlation coefficients between non-power bogie components form the matrix A(2).
| $ \boldsymbol{A}^{(1)}=\left(\begin{array}{ccc} \gamma_{11}^{(1)} & \cdots & \gamma_{1 n}^{(1)} \\ \vdots & \ddots & \vdots \\ \gamma_{n 1}^{(1)} & \cdots & \gamma_{n n}^{(1)} \end{array}\right) $ | (4) |
| $ \boldsymbol{A}^{(2)}=\left(\begin{array}{ccc} \gamma_{11}^{(2)} & \cdots & \gamma_{1 n}^{(2)} \\ \vdots & \ddots & \vdots \\ \gamma_{n 1}^{(2)} & \cdots & \gamma_{n n}^{(2)} \end{array}\right) $ | (5) |
Considering the influence of other components on the failure rate of component i, the actual failure rate of component i is given:
| $ \boldsymbol{\lambda}_i(l)=\boldsymbol{\lambda}_i^I(l)+\sum\limits_{j \in \boldsymbol{V}_{\mathrm{p}}} \boldsymbol{\gamma}_{i j}^{(1)} \boldsymbol{\lambda}_j(l), i \in \boldsymbol{V}_{\mathrm{p}} $ | (6) |
| $ \boldsymbol{\lambda}_i(l)=\boldsymbol{\lambda}_i^I(l)+\sum\limits_{j \in V_{\mathrm{np}}} \gamma_{i j}^{(2)} \boldsymbol{\lambda}_j(l), i \in \boldsymbol{V}_{\mathrm{np}} $ | (7) |
where γij(1) is the element of matrix A(1), γij(2) is the element of matrix A(2).
Taking the components in the power bogie as an example, the initial failure rate of the components consists of the vector λI=[λ1I, ..., λ4I]T. The actual failure rate vector is given:
| $ \boldsymbol{\lambda}=\boldsymbol{\lambda}^I+\boldsymbol{A}^{(1)} \boldsymbol{\lambda} $ | (8) |
| $ \left(\boldsymbol{I}-\boldsymbol{A}^{(1)}\right) \boldsymbol{\lambda}=\boldsymbol{\lambda}^I $ | (9) |
| $ \boldsymbol{\lambda}=\left(\boldsymbol{I}-\boldsymbol{A}^{(1)}\right)^{-1} \boldsymbol{\lambda}^I $ | (10) |
where I is unit matrix of n dimensions. We assume D=(I-A(1))-1, and it is derived that λ=DλI. dij is the element of the ith row and jth column of D. Then the reliability is given:
| $ \begin{aligned} R_i(l)= & \exp \left(-\int_0^l \lambda_i(s) \mathrm{d} s\right)= \\ & \exp \left(-\int_0^l\left(\sum\limits_{j \in V_p} d_{i j} \lambda_i^I(s)\right) \mathrm{d} s\right)= \\ & \prod\limits_{j \in V_p} \exp \left(-d_{i j} \int_0^l \lambda_j^I(s) \mathrm{d} s\right) \end{aligned} $ | (11) |
Similarly, we can derive the failure rate and reliability of components in the non-power bogie.
2.2 Maintenance Costs ModellingPreventive maintenance and minimal repair are applied to maintenance of EMU trains in this paper. Therefore, the maintenance costs include preventive maintenance costs and minimal repair costs.
The preventive maintenance costs of component i are given:
| $ C_i^{\mathrm{p}}=c^{\mathrm{set}}+c_i^{\mathrm{up}} $ | (12) |
where cset denotes the fixed set-up cost, ciup denotes the unit preventive maintenance cost.
The minimal repair costs are given:
| $ C_i^{\mathrm{c}}=\int_0^{L_{\max }} \varepsilon_k c_i^{\mathrm{cu}} \lambda_i(l) \mathrm{d} l $ | (13) |
where cicu denotes the unit minimal repair cost.
When preventive maintenance is carried out on any component, we can implement preventive maintenance for other components simultaneously to reduce fixed costs. Therefore, the cost of the jth downtime of the system for maintenance is given:
| $ C^{\mathrm{total}}=\sum\limits_{i \in V} C_i^{\mathrm{p}}+\sum\limits_{i \in V} C_i^{\mathrm{c}}-\Delta N_{\mathrm{om}}\left(c^{\mathrm{set}}+c^{\mathrm{d}}\right) $ | (14) |
where ΔNom denotes the number of saving fixed costs.
3 Dynamic Maintenance StrategyIn this paper, a dynamic maintenance strategy based on environmental changes is proposed to solve this problem. The preventive maintenance thresholds are different with the fluctuation of environmental factors and the maintenance strategy is more flexible.
3.1 Thresholds SettingIn traditional opportunistic maintenance strategy, a pair of reliability thresholds (Rpm, Rom) are set. When the reliability of any component is lower than Rpm, preventive maintenance is implemented on other components whose reliabilities are lower than Rom at the same time. In the dynamic maintenance strategy, (Rpmk, Romk) is set for each interval k. There are θ pairs of reliability thresholds (Rpm1, Rom1), ..., (Rpmθ, Romθ), so the reliability thresholds are more flexible to adapt to the environmental change.
3.2 Decision-making ProcessThe flow chart of the dynamic maintenance strategy is shown in Fig. 2. The steps to be performed are as follows:

|
Fig.2 Flow chart of dynamic maintenance strategy |
1) Input initial parameters, including Weibull distribution parameters, thresholds, cost coefficients, environmental parameters, and fault correlation matrix.
2) Obtain the environmental interval and reliability thresholds for the interval.
3) Calculate the reliability and failure rate under the influence of fault correlations and environment.
4) Determine whether there are components with reliability below Rpmk, if so, skip to 5); if not, skip to 9).
5) Add the components that require preventive maintenance to the maintenance set V.
6) Determine if there are components with reliability below Romk. If so, skip to 7); if not, skip to 9).
7) Add the components that require maintenance to the maintenance set V.
8) Calculate the maintenance costs according to set V.
9) Determine if the total mileage exceeds Lmax. If yes then skip to 10); otherwise, l=l+1, skip to 2).
10) Calculate the total maintenance costs and output the result.
3.3 Thresholds OptimizationThere are θ pairs of reliability thresholds (Rpm1, Rom1), ..., (Rpmθ, Romθ) in the dynamic maintenance strategy and it is difficult to determine the optimized values. We apply artificial bee colony algorithm to optimize the thresholds. The artificial bee colony algorithm is a meta-heuristic algorithm with high robustness and high accuracy. In this paper, the artificial bee colony algorithm (Fig. 3) is suitable due to the complex calculation of the objective function and the high accuracy requirements in the solution[22].

|
Fig.3 Flow chart of artificial bee colony algorithm |
(Ⅰ) Initialization
An array of 2 rows and θ columns is applied to represent a solution, as shown in Fig. 4.
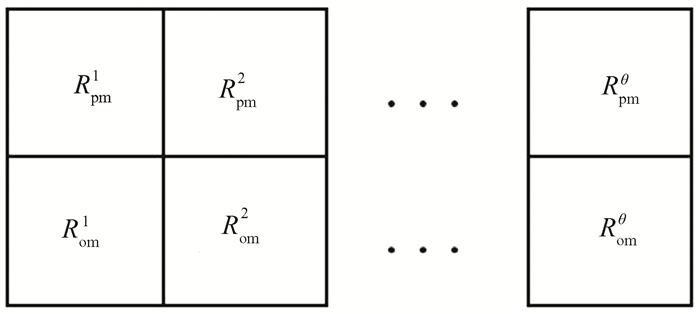
|
Fig.4 Encoding form |
The initial solutions are generated from continuous random variables within[0, 1]. Each solution corresponds to an employed bee.
(Ⅱ) Employed bees
In the algorithm, employed bees search for better neighboring solutions. We assume the corresponding solution of the employed bee is p1. Choose a solution p2 randomly from the solution set. The generating neighboring solution is given:
| $ \boldsymbol{p}_{\mathrm{nei}}=\boldsymbol{p}_1+\xi\left(\boldsymbol{p}_2-\boldsymbol{p}_1\right) $ | (15) |
If pnei achieves a better objective than that of p1, p1 is replaced by pnei. Otherwise pnei is abandoned.
(Ⅲ) Onlooker bees
According to Section 2, we can calculate the objective function Citotal of each solution. The average value of all the objective functions is Cave. Then the fitness of each solution is given:
| $ f_i=\exp \left(-C_i^{\text {total }} / C^{\text {ave }}\right) $ | (16) |
The selection probability is calculated:
| $ p_i^{\mathrm{fo}}=\frac{f_i}{\sum\limits_{j=1}^{N_{\mathrm{ne}}} f_j} $ | (17) |
Each onlooker bee would select a solution by selection probability. The solutions which are not selected would be abandoned.
(Ⅳ) Scout bees
Each scout bee searches solutions in the entire solution space. If any solution is better than the current best solution, the solution is added to the solution set.
4 Numerical AnalysisIn this paper, the bogie system of EMU train is the research object for result analysis. According to the maintenance outline of EMU trains, there are 5 levels of maintenance procedure. The maintenance of bogie system belongs to Level 3. The structure is illustrated in Section 1.
According to Ref.[15], the composition of the bogies of EMU trains and their correlations have been analyzed in detail. The component composition of the power bogie is X1(Traction motor), X2(Coupling joint), X3(Gearboxes), and X4(Rotation pair), Vp={X1, X2, X3, X4}.
The failure correlation matrix of the power bogie is given:
| $ \begin{aligned} & \begin{array}{llll} &&&&&&X_1 & X_2 & X_3 & X_4 \end{array} \\ & \boldsymbol{A}^{(1)}=\begin{array}{c} X_1 \\ X_2 \\ X_3 \\ X_4 \end{array}\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0.05 & 0 & 0 & 0 \\ 0 & 0.07 & 0 & 0 \\ 0 & 0.02 & 0.1 & 0 \end{array}\right) \\ & \end{aligned} $ |
The component composition of the non-power bogie is X5(Rotation pair), X6(Brakes), X7(Axle box), and X8(Gate sheet), Vnp={X5, X6, X7, X8 }. The failure correlation matrix of the non-power bogie is given:
| $ \begin{aligned} & \begin{array}{llll} &&&&&&X_5 & X_6 & X_7 & X_8 \end{array} \\ & \boldsymbol{A}^{(2)}=\begin{array}{l} X_5 \\ X_6 \\ X_7 \\ X_8 \end{array}\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0.07 & 0 & 0 & 0 \\ 0.1 & 0 & 0 & 0 \\ 0 & 0.06 & 0 & 0 \end{array}\right) \\ & \end{aligned} $ |
Referring to the data in Ref.[23], Weibull parameters and cost coefficients are shown in Table 1. The ratio of two type of unit costs cuc/cup=3, which would be analysed.
| Table 1 Component parameters |
The fixed set-up cost cset=500. Environmental factors[4] within [0, Ly] are shown in Table 2.
| Table 2 Environmental impact factor |
The reliability evolution of the components throughout the time window is shown in Fig. 5. When the reliability of one component is restored by maintenance, the reliability of its interacting components also improves. As shown in Fig. 5(a), when the first maintenance (42×104km) is performed, the reliability of X3 and X4 changes even though they are under no preventive maintenance. The curvature of the reliability of the components under the influence of environmental factors varies in different intervals. As can be observed in Fig. 5(b), the curvature of the reliability curve of the components changes several times.
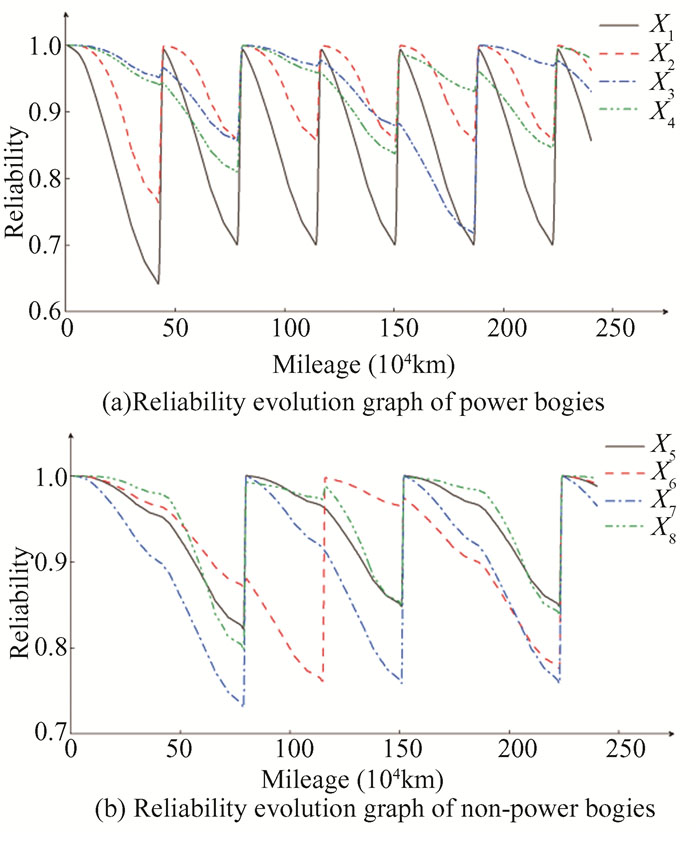
|
Fig.5 Reliability evolution graph of power bogies and non-power bogies |
Dynamic maintenance strategy is proposed for maintenance planning, while the artificial bee colony algorithm is applied for optimization of maintenance thresholds. In the artificial bee colony algorithm, the initial number of solutions is set to 40 and the maximum iteration is set to 400. Table 3 shows the optimization results of the dynamic maintenance decision method. The results show that the dynamic maintenance strategy is able to combine the maintenance of different components in a reasonable way, reducing downtime as well as fixed set-up costs.
| Table 3 Maintenance scheduling optimization results |
The traditional opportunistic maintenance strategy is compared with the strategy proposed in the paper. The comparison of the two strategies is shown in Fig. 6. It can be observed that the initial solution of the dynamic repair strategy outperforms the traditional opportunistic maintenance strategy. The dynamic strategy results in lower maintenance costs as well as faster convergence.
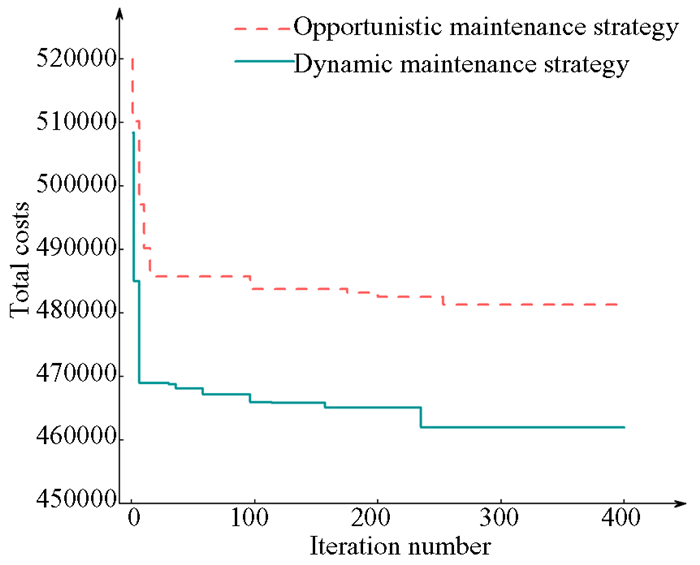
|
Fig.6 Algorithm iteration and comparison chart |
Table 4 shows the comparison of the specific optimization results of the two maintenance strategies. The traditional opportunistic maintenance strategy thresholds are limited to a fixed value, which makes it difficult to adjust the environmental changes and generates higher preventive maintenance costs. The dynamic maintenance strategy, on the other hand, canreduce preventive maintenance costs by dynamically adjusting the thresholds to make the decisions more flexible.
| Table 4 Comparison of the results of different maintenance strategies |
Table 5 shows the fluctuation of the dynamic maintenance strategy with the change of the fault correlation coefficient. Each fault correlation coefficient is increased by 0.05 and the costs are analyzed separately. The results show that the adjustment of the fault correlation coefficients mainly affects the costs of minimum repair. The fault correlation coefficients can affect the change pattern of the failure rate, which increases the expected number of minimum repairs.
| Table 5 Sensitivity analysis of failure correlation coefficients |
A sensitivity analysis is performed on the cost parameters of the components, as shown in Table 6. cuc/cup reflects the proportional relationship between the minimal repair cost and the preventive maintenance cost. cset is fixed set-up cost. When cuc/cup increases, the minimal repair costs will theoretically increase proportionally. The dynamic maintenance strategy suppresses the increase of minimal repair costs by adjusting the maintenance schedule. For example, when cset=500 and cuc/cup=3, the minimal repair cost is ¥205401. When cset=500 and cuc/cup=10, the minimal repair cost is ¥589657. When cset increases, the preventive maintenance cost increase, but the fixed cost savings also increase. Finally, the total costs growth is controlled. When cuc/cup=3, cset is set to 500 and 2500, the total costs are ¥462001 and ¥470595, respectively.
| Table 6 Sensitivity analysis of cost parameters |
The results show that the dynamic maintenance strategy proposed in this paper outperforms the traditional opportunistic maintenance strategy. The maintenance model can provide assistance in making better decisions for EMU trains. However, there are many other factors that could be further considered. The maintenance effectiveness, personnel cost, and storage cost would change with different maintenance strategies. Considering these factors, some novel methods need to be proposed to deal with the complex problems of EMU trains maintenance. There are many real maintenance scenarios for each maintenance action. Under each scenario, the maintenance costs may be different, which also influences the decision-making for maintenance plans. The situations and details are not considered adequately in this paper due to the limitation of the related data and research.
5 ConclusionsThis paper analyzes the evolution of the reliability and failure rate of EMU trains under the influence of environmental factors, fault correlations and economic correlations. We establish a maintenance model for EMU trains considering environmental factors and multiple correlations with the lowest total maintenance cost as the optimization objective. A dynamic maintenance strategy is proposed for this model, which optimizes the maintenance plan by setting maintenance thresholds flexibly. An artificial bee colony algorithm is applied to optimize the parameters in the strategy. The results show that the dynamic maintenance strategy can effectively reduce costs and outperforms the traditional opportunistic maintenance strategy. Sensitivity analysis is also conducted to confirm the stability of the model.
This paper can provide reference and theoretical basis for the maintenance plan of EMU trains. In the future study, the effectiveness of the maintenance model can be verified by practical application of maintenance plans for EMU trains.
| [1] |
Li Y, Qi Feng, Yin P F, et al. Study on preventive maintenance cycle of sliding plug door of high-speed train in strong blown-sand area. Journal of Central South University (Science and Technology), 2018, 49(09): 2344-2349. DOI:10.11817/j.issn.1672-7207.2018.09.030 (  0) 0) |
| [2] |
Xiao Y R, Zhang G Q. Technology research on weather-resistance for Lan-Xin line EMU. Railway Locomotive & Car, 2014, 34(04): 90-93. (  0) 0) |
| [3] |
Xing H Y, Li S X, Xiao Y R. Technical research on multiple units adaptability to track of Lanxin line. Rolling Stock, 2014, 52(6): 1-5+60. (  0) 0) |
| [4] |
Han C G. Operation and Maintenance Requirement Research of Lanzhou-Xinjiang High-Speed Railway for CRH. Beijing: China Academy of Railway Sciences, 2015.
(  0) 0) |
| [5] |
Hu J, Jiang Z, Liao H. Preventive maintenance of a single machine system working under piecewise constant operating condition. Reliability Engineering & System Safety, 2017, 168: 105-115. DOI:10.1016/j.ress.2017.05.014 (  0) 0) |
| [6] |
Lan J, Yuan H J, Yuan M, et al. System reliability assessment under real time-varying environmental stress. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 406-412. DOI:10.13700/j.bh.1001-5965.2017.0120 (  0) 0) |
| [7] |
Xia T B, Xi L F, Lee J, et al. Optimal cbpm policy considering maintenance effects and environmental condition. The International Journal of Advanced Manufacturing Technology, 2011, 56(9): 1181-1193. DOI:10.1007/s00170-011-3235-4 (  0) 0) |
| [8] |
You M-Y, Li H G, Meng G. Control-limit preventive maintenance policies for components subject to imperfect preventive maintenance and variable operational conditions. Reliability Engineering & System Safety, 2011, 96(5): 590-598. DOI:10.1016/j.ress.2010.12.015 (  0) 0) |
| [9] |
Hu J W, Xu A C, Li B, et al. Condition-based maintenance planning for multi-state systems under time-varying environmental conditions. Computers & Industrial Engineering, 2021, 158: 107380. DOI:10.1016/j.cie.2021.107380 (  0) 0) |
| [10] |
Li L, Jin L, Zhou X J. Preventive maintenance strategy based on shock modeling for leasing equipment. Computer Integrated Manufacturing Systems, 2013, 19(1): 114-118. (  0) 0) |
| [11] |
Eryilmaz S, Tekin M. Reliability evaluation of a system under a mixed shock model. Journal of Computational and Applied Mathematics, 2019, 352: 255-261. DOI:10.1016/j.cam.2018.12.011 (  0) 0) |
| [12] |
Yang L, Ma X B, Peng R, et al. A preventive maintenance policy based on dependent two-stage deterioration and external shocks. Reliability Engineering & System Safety, 2017, 160: 201-211. DOI:10.1016/j.ress.2016.12.008 (  0) 0) |
| [13] |
Thomas L C. A survey of maintenance and replacement models for maintainability and reliability of multi-item systems. Reliability Engineering, 1986, 16(4): 297-309. DOI:10.1016/0143-8174(86)90099-5 (  0) 0) |
| [14] |
Liu Q M. Research on Methods for Condition Based Equipment Health Prognosis and Integrated Maintenance Model. Shanghai: Shanghai Jiao Tong University, 2014.
(  0) 0) |
| [15] |
Wang H, Du W X, Liu Z L, et al. Integrating failure and economic dependence for maintenance of electric multiple unit multi-component system. Journal of Shanghai Jiao Tong University, 2016, 50(5): 660-667. (  0) 0) |
| [16] |
Vu H C, Do P, Barros A. A study on the impacts of maintenance duration on dynamic grouping modeling and optimization of multicomponent systems. IEEE Transactions on Reliability, 2018, 67(3): 1377-1392. DOI:10.1109/TR.2018.2827926 (  0) 0) |
| [17] |
Bouvard K, Artus S, Berenguer C, et al. Condition-based dynamic maintenance operations planning & grouping. Application to commercial heavy vehicles. Reliability Engineering & System Safety, 2011, 96(6): 601-610. DOI:10.1016/j.ress.2010.11.009 (  0) 0) |
| [18] |
Do P D, Barros A, Berenguer C, et al. Dynamic grouping maintenance with time limited opportunities. Reliability Engineering & System Safety, 2013, 120: 51-59. DOI:10.1016/j.ress.2013.03.016 (  0) 0) |
| [19] |
Kou L L, Qin Y, Zhao X J, et al. Integrating synthetic minority oversampling and gradient boosting decision tree for bogie fault diagnosis in rail vehicles. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2019, 233(3): 312-325. DOI:10.1177/0954409718795089 (  0) 0) |
| [20] |
Sun Y, Ma L, Mathew J, et al. An analytical model for interactive failures. Reliability Engineering & System Safety, 2006, 91(5): 495-504. DOI:10.1016/j.ress.2005.03.014 (  0) 0) |
| [21] |
Wang H, Xiong L, He Y, et al. Optimization of opportunistic maintenance for electric multiple unit component considering failure risk. Journal of the China Railway Society, 2019, 41(3): 79-85. DOI:10.3785/j.issn.1006-754X.2022.00.026 (  0) 0) |
| [22] |
He Y, Liu J H, Yang R H. Survey on artificial bee colony algorithm. Application Research of Computers, 2018, 35(5): 1281-1286. (  0) 0) |
| [23] |
Zheng J C. Research on the Reliability of Bogie System of High-Speed Train. Beijing: Beijing Jiaotong University, 2016.
(  0) 0) |
 2023, Vol. 30
2023, Vol. 30


