Optimization with multiple objective functions is called multi-objective optimization problems (MOPs) [1]. Since multiple objective functions often conflict with each other, MOPs are more complex than single objective optimization problems (SOPs). When MOPs have more than three objective functions, they are mentioned as many-objective optimization problems (MaOPs) [2-3]. MaOPs have more objective functions than MOPs, which makes solving more challenging.
multi-objective evolutionary algorithms (MOEAs) can solve MOPs that simulate natural biological evolution processes [4]. Traditional MOEAs can get better performance when dealing with MOPs; however, there will be a series of problems when dealing with MaOPs [5]. One of the important problems is that more objective functions will produce a large number of non-dominated solutions, and sometimes the whole population will be non-dominated solutions. Too many non-dominated solutions will make the environmental-selection strategy based on non-dominated relations fail.
Researchers have proposed a series of improved algorithms to meet the challenge brought about by the increased objectives. These algorithms are divided into the decomposition-based algorithm, laxity-based algorithm, and Indicator-based algorithm. The decomposition-based algorithm decomposes a MaOP into simple SOPs or MOPs, and it solves and merges these subproblems separately to obtain the solution to the MaOP. The representatives of such algorithms are the multi-objective evolutionary algorithm based on decomposition (MOEA/D) [6], reference-vector-guided evolutionary algorithm (RVEA)[7], and non-dominated sorting genetic algorithm III (NSGA-III) [8].
The laxity-based algorithm modifies the dominating relationship to expand the dominating region of the solution and alleviate the dominating failure to a certain extent. Such algorithms proposed recently include the many-objective evolutionary algorithm adopting dynamic angle vector-based dominance relation (DAV-MOEA) [9], many-objective particle swarm optimization based on adaptive fuzzy dominance (MAPSOAF)[10], etc.
Indicator-based algorithm proposes an indicator to map the objective values to a certain number, and the indicator is also used for environmental selection or mating selection.Immune-inspired resource allocation strategy for many-objective optimization (MaOEA/IRAS) [11] is a new indicator-based algorithm. The sparse region theory in Ref. [11] proposes a new indicator, which defined by the Euclidean distances of their projected points on the unit hyperplane. Solutions far from hyperplane are considered to be in the sparse region.The algorithm has less exploration in the sparse region, and exploring the region can increase the diversity of the algorithm. The indicator-based evolutionary algorithm (IBEA) [12] is the first Iε+-indicator-based algorithm and provides a common framework for indicator-based methods.
The IBEA can be combined with arbitrary indicators. Although binary performance measure Iε+(x, y) can be combined with arbitrary indicators, directly using Iε+(x, y) into the selection process also has good performance. The IBEA proposes a fitness function based on Iε+(x, y) (fitness assignment), which considers the individual information of the entire population to evaluate individuals. Iε+(x, y) can be directly used for environmental selection (worst contribution) to balance the diversity and convergence, and only the information between two solutions is used for selection. The many-objective evolutionary algorithm based on indicator Iε+(x, y) is proposed.
1 Propaedeutics 1.1 Indicator-based AlgorithmClassification method [13] classifies IB mechanisms into two main categories: IB Selection (IB-environmental selection, IB-density estimation, and IB-archiving) and IB-mating selection. Many-objective metaheuristics based on the R2 indicator (MOMBI)[14] and Indicator-based evolutionary algorithm (IBEA) use the IB-environmental selection mechanism. The hypervolume estimation algorithm (HypE)[15] and IGD-based many-objective evolutionary algorithm (MaOEA/IGD)[16] use the IB-density estimator. The adaptive archiving algorithm for storing nondominated vectors (LAHC) [17] uses IB-archiving methods.IB-mating selection involves the identification of good parent solutions based on quality indicator values. IB-mating selection mechanisms are used by the R2 Indicator-based evolutionary algorithm for multi-objective optimization (R2-IBEA) [18], MaOEA/IGD, and adaptive reference points-based multi-objective evolutionary algorithm (ARMOEA)[19].
1.2 Indicator Iε+(x, y)A general optimization problem is defined by d-dimensional decision space X, m-dimensional objective space Y, and m objective functions f1, f2, f3, …, and fm.
y=(f1(x), f2(x), f3(x), …, fm(x))∈Y for each decision variable x=(x1, x2, …, xd)∈X. All objective functions are assumed to be minimized, and
| $ \begin{gathered} I_{\varepsilon+}\left(\boldsymbol{x}^1, \boldsymbol{x}^2\right)=\min _{\varepsilon}(\forall i \in\{1, 2, \cdots, m\}, \\ \left.\exists y_i^1-\varepsilon \leqslant y_i^2\right) \end{gathered} $ | (1) |
where x1 and x2∈X; yi1∈y1; yi2∈y2; y1 and y2 are the mappings of x1 and x2 on the objective space.
Iε+(x, y) can be regarded as the enhancement of Pareto dominance, and Iε+(x, y) can be directly used as a fitness value; therefore, Iε+(x, y) is used in the work. The two-objective problem is taken as an example (see Fig. 1).
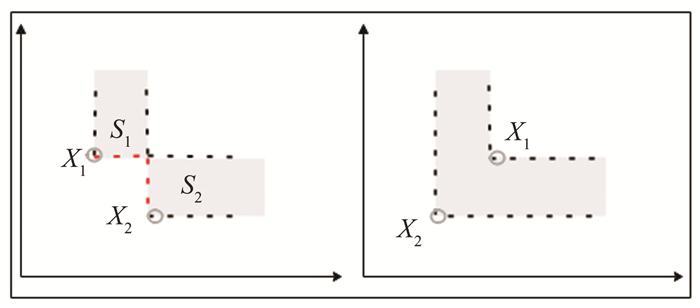
|
Fig.1 Two cases of Iε+(x, y) |
Two solutions X1 and X2 do not dominate each other on the left. S1 and S2 represent the distance between X2 and X1 on object 1 and that between X1 and X2 on object 2, respectively. Iε+(X1, X2)=S2. S2 is interpreted as that if X1 wants to dominate X2, S2 needs to be optimized at least. Similar to Iε+(X2, X1)=S1, if X2 wants to dominate X1, S1 needs to be optimized at least. Two solutions X1 and X2 are on the right, and X2 dominates X1. Iε+(X2, X1) < 0, that is, when Iε+(x, y) < 0, x dominates y.
2 Proposed MaOEA/I 2.1 Framework of MaOEA/IThe overall framework of the proposed MaOEA/I is presented in Algorithm 1.
Algorithm1 General Framework of MaOEA/I
Input : N (population size), maxFE (maximum function evaluation times) Output : P (final population) 1: P=Initialization(N) 2: while FE < maxFE do 3: MatingPool=TournamentSelection(P) 4: O=Reproduction(MatingPool) 5: Pt=P∪O 6: P=EnvironmentalSelection(Pt) 7: end while 8: Return P
The MaOEA/I starts from randomly initialized population P containing N individuals. Afterward, P undergoes an evolution procedure. Offspring population O is first generated in each generation by performing mating selection, simulated binary crossover [20], and polynomial mutation [21] on P.Second, P and O are merged to form new population Pt of 2N individuals. Finally, environmental selection is performed to select N elite individuals. The evolution procedure is repeated until the termination criterion is satisfied. The mating selection and environmental selection of the MaOEA/I are introduced in the following sections.
2.2 Mating SelectionThe binary tournament selection method is used for a mating selection. Function F based on Iε+(x, y) is used as the fitness value of the mating selection (see Eq. (2)).
| $ F_x=-\min I_{\varepsilon^{+}}\left(x, x_i\right), x_i \in P /\{x\} $ | (2) |
where Fx is the fitness value of individual x; xi is the other individual except for x in population P.
2.3 Environmental SelectionEnvironmental selection mainly depends on fitness assignments in the IBEA.
| $ F\left(x_1\right)=\sum _{x_2 \in P /\left\{x_1\right\}}-e^{-I\left(x_2, x_1\right) / \kappa} $ | (3) |
where P is the population; κ the fitness scaling factor. Fitness F(x) is related to Iε+(x, y) between x and the whole population without itself.
The MaOEA/I has no fitness for the individual.Indicator Iε+(x, y) can measure individuals by its value. Iε+(x, y) is directly used to evaluate the quality of individuals.
A population of 100 individuals is taken as an example, and each iteration produces 100 new individuals.Both the IBEA and MaOEA/I need to calculate Iε+(x, y) between each individual. TheIBEA uses Iε+(x, y) to calculate the fitness of the 200 individuals, while the MaOEA/I uses Iε+ as the indicator of environmental selection. Although the environmental selection of the MaOEA/I needs to consider more values and the situation is more complex (with 200 fitness of IBEA and 200×199 Iε+), it can more accurately select the individual with the lowest contribution.
The environmental selection procedure of the proposed MaOEA/I is presented in Algorithm 2.
Algorithm 2 Environmentals election
Input: Pt (temporary population), count (number of individuals in Pt), and N (population size) Output: P (final population) 1: I=CalculationI(Pt, 2N) 2: Sort I from small to large 3: i=1 4: while count>N do 5: Get the elements in I (defined as Ii) and corresponding individuals xi, yi in order 6: if xi∈Pt∧yi∈Pt, then 7: Delete yi from Pt 8: count=count-1 9: end if 10: i=i+1 11: end while 12: P=Pt 13: Return P
Calculate Iε+(x, y) of temporary population Pt, and sort I from small to large. When Iε+(x, y)≤0, x dominates y.Smaller Iε+(x, y) means greater dominance. When Iε+(x, y)>0, the closer x is to y, the smaller Iε+(x, y) is. Therefore, the work gives priority to deleting the most dominant individual. When all the dominant individuals are deleted and the number of individuals in temporary population Pt is still larger than N, one of the closest two individuals is deleted. The inferior individuals are deleted from Pt one by one until the number of individuals in Pt is N.The individuals with poor convergence and diversity in the population are gradually eliminated by repeating the above operations, and the population converges and is evenly distributed on the Pareto front (see Fig. 2).

|
Fig.2 Flow of environmental selection |
Iε+(x, y) calculation procedure is presented in Algorithm 3. In particular, when i=j, I(i, j)=+∞ is set because Iε+(x, y) cannot be calculated for the same individual.
2.4 Calculation of Iε+(x, y)
Algorithm 3 Calculation I
Input: P (population) and N (population size) Output: I (Iε+ matrix) 1: Normalize the objective values of all individuals in P 2: Generate matrix I of N×N, the value of the element in the matrix is +∞ 3: for i=1∶N do 4: for j=1∶N do 5: if i≠j do 6: Calculate Iε+(xi, xj) by Eq. (1) and fill in storage matrix I(i, j) 7: end if 8: end for 9: end for 10:Return I
The computational complexity of the proposed MaOEA/I mainly depends on the mating selection and environmental selection. The computational complexity of the mating selection is O(N2) in the worst case. Environmental selection includes the calculation of Iε+(x, y), sort, and deletion. The calculation of Iε+(x, y) includes O(2mN) required for normalization. m is the objective number of the problem, and the calculated value of Iε+(x, y) requires O(4mN2). Sort requires O(4N2log2(2N)), and deletion requires O(2N). Overall, the computational complexity of MaOEA/I is O(N2)+ O(2mN)+O(4mN2)+O(4N2log2(2N))+O(2N)= O((4m+log2(2N))N2).
3 Experiment and DiscussionThe proposed MaOEA/I was compared with other 6 algorithms, including IBEA[11], MOMBI-II [22], MaOEA/IGD [15], NSGA-III [8], RPEA [23], and RVEA, to test its performance in MaOPs. This section describes the test problems, performance indicator, experimental environment, parameter settings used in the experimental study, results, and discussion.
3.1 Test ProblemsMaF [24] test problems are used to verify the performance of the MaOEA/I. MaF test problems have many properties of the Pareto Front, which can test the performance of solving MaOPs from many aspects.
The number of objective M is 5, 10, 15, and 25, respectively. The default values of the number of decision variable D is used for MaF test problems. Calculate D with D=M+K-1 in MaFs 1-12, and K=10. Calculate D with D=M+K-1 in MaF 7, and K=20. D is fixed to 2 in MaFs 8 and 9. Calculate D with D=M×20 in MaFs 14 and 15.
3.2 Performance IndicatorInverse generation distance (IGD) [25] and Hypervolume (HV) [26] were used to evaluate the convergence and diversity of results. Each algorithm was independently executed 30 times on each test problem to reduce the impact of random factors on performance evaluations. The Wilcoxon rank sum test with a significance level of 0.05 was used to discuss the difference in algorithm performance.
3.3 Experimental EnvironmentThe computer was configured with 16G memory, Intel (R) Core (TM) i7-10875H CPU@2.30GHz processor, and Windows10 X64 system. All algorithms were compared on PlatEMO [27] based on MATLAB, and the version of the PlatEMO was v3.5.
3.4 Parameter SettingsThe population size with 5, 10, 15, and 25 objectives were 150, 200, 250, and 300, respectively. The termination condition was that the algorithm had exhausted the number of evaluations. The maximum number of evaluations was 100000. All evolutionary algorithms in the work used binary crossover and polynomial mutation to generate offspring. The crossover probability and mutation probability were set to 1.0 and 1/D, and D was the number of decision variables. The fitness scaling factor of IBEA was set to 0.5. The number of evaluations for nadir point estimation of the MaOEA/IGD was set to 100×N.The parameter controlling the rate of change of penalty in RVEA was set to 2, and the frequency of employing reference vector adaptation was set to 0.1. The variance threshold, tolerance threshold, and record size of nadir vectors of MOMBI-II were set to 0.5, 0.001, and 5. The ratios of individuals used to generate reference points and parameters determining the difference between the reference point and the individuals of RPEA were set to 0.4 and 0.1, respectively. There was no need to set parameters for the MaOEA/I.
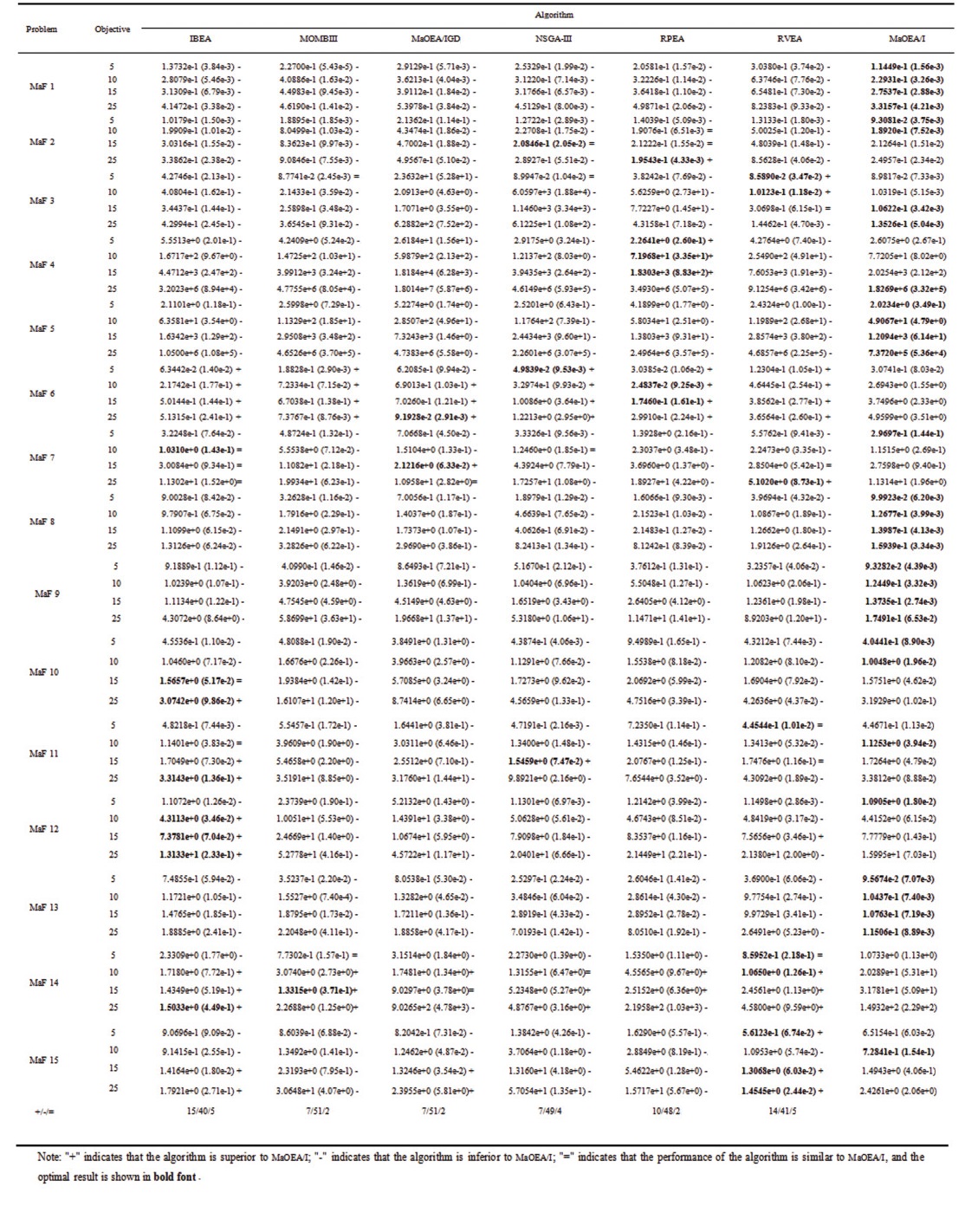
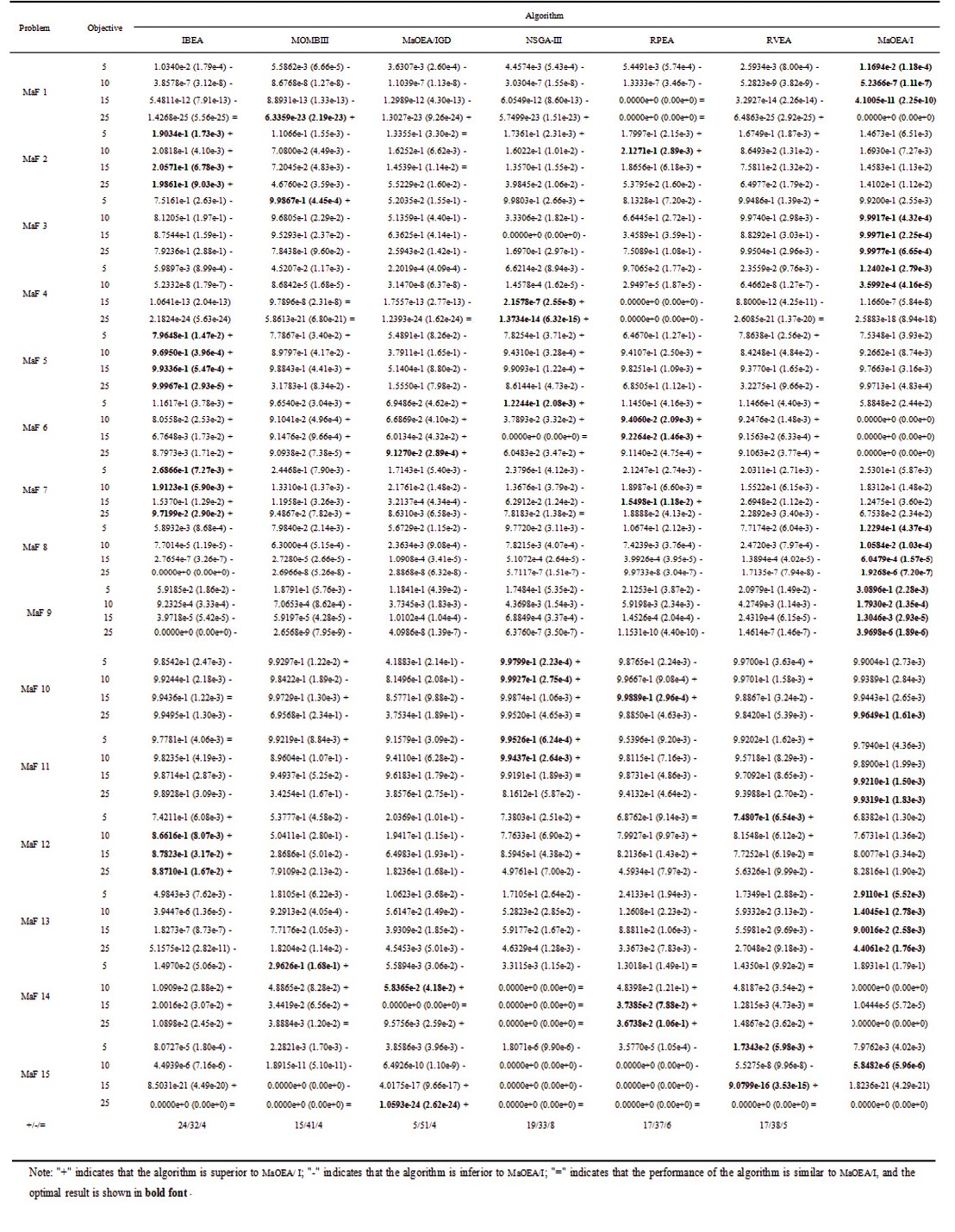
3.5 Results and DiscussionTables 1 and 2 show the results of each algorithm on MaF(5-objective). The IBEA, MOMBI-II, MaOEA/IGD, NSGA-III, RPEA, RVEA, and MaOEA/I are in columns 1-7, respectively.
| Table 1 Results of IGD |
| Table 2 Results of HV |
The MaOEA/I obtains significantly better performance on MaF testing problems with different dimensions and different difficulties (see Table 1). Although the performance of the MaOEA/I is not as good as that in Table 1, the MaOEA/I is still better than other algorithms (see Table 2). Fig. 3 shows the IGD changing curves of MaFs 1, 3, 5, 6, 7, and 13. IGD values obtained by the MaOEA/I in the 6 test problems can rapidly converge to a relatively good position and continue to optimize, which shows its performance in balancing convergence and diversity. The IGD of the IBEA, MaOEA/IGD, NSGA-III, RVEA, and MOMBIII fluctuates during the search process (see Fig. 3 (f)).
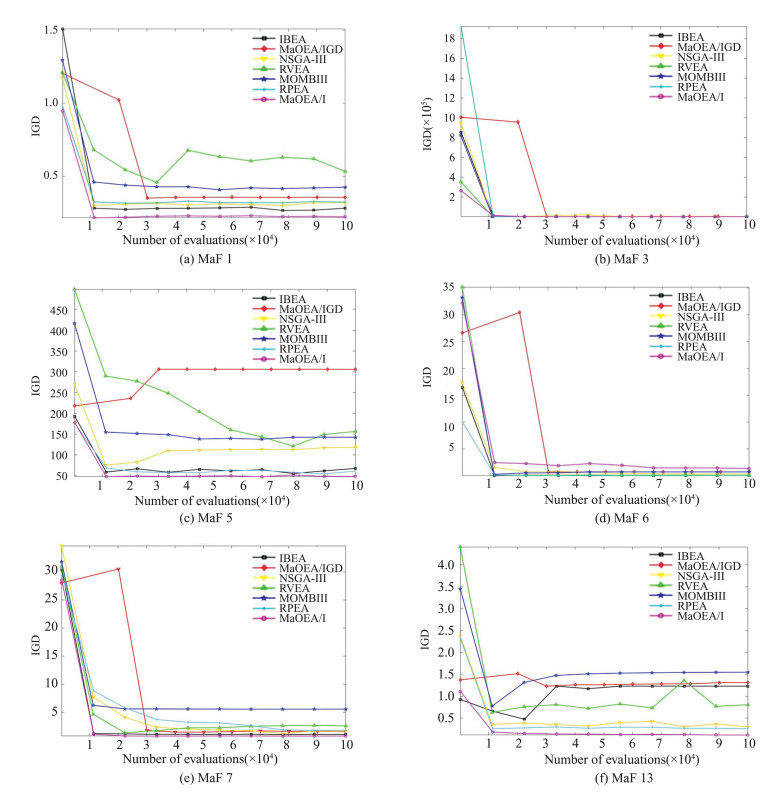
|
Fig.3 IGD changing curves |
Table 3 shows the average running time of the algorithm for calculating MaFs. Environmental selection is more complex and the computation will increase with the expansion of the population; therefore, the MaOEA/I has no advantage over other algorithms in running time.
| Table 3 Running time |
Fig. 4 shows IGD on 5-objective MaFs.

|
Fig.4 IGD on 5-objective MaFs |
The MaOEA/I can obtain stable results on most problems in 30 repeated experiments, and it is only inferior to other algorithms on MaFs 6 and 15.
4 ConclusionsAiming at the environmental selection strategy based on non-dominated relation failure and the difficulty in the balance of convergence and diversity in MaOPs, the work proposed the MaOEA/I. The MaOEA/I used Iε+(x, y) for environmental selection. Iε+(x, y) could select the dominated solution and the solution close in space with the strengthening non-dominated relationship, which considers convergence and diversity.
The IBEA focused on global information and usedfitness assignment using Iε+(x, y); however, MaOEA/I used the local meaning and worst contribution. If two solutions were too close, no matter where they were in the population, one of them must be deleted. It solved the environmental selection strategy based on non-dominated relation failure and contributed to dealing with the irregular Pareto front. The experimental results showed that the MaOEA/I has a good performance on MaF problems, with effectiveness in balancing convergence and diversity.
| [1] |
Zhou A, Qu B, Li H, et al. Multi-objective evolutionary algorithms: a survey of the state of the art. Swarm and Evolutionary Computation, 2011, 1(1): 32-49. DOI:10.1016/j.swevo.2011.03.001 (  0) 0) |
| [2] |
Sun J, Gong D-W. Recent advances in evolutionary many-objective optimization. Control Theory & Applications, 2018, 35(7): 928-938. DOI:10.7641/CTA.2018.80067 (  0) 0) |
| [3] |
Liu J C, Li F, Wang H H, et al. Survey on evolutionary many-objective optimization algorithm. Control and Decision, 2018, 35(5): 114-122. DOI:10.13195/j.kzyjc.2017.1442 (  0) 0) |
| [4] |
Deb K. Multi-objective Optimization Using Evolutionary Algorithms. England: John Wiley and Sons, 2001. 13-49.
(  0) 0) |
| [5] |
Chen Zhen-Xing, Yan Xuan-Hui, Wu Kun-An, et al. Many-objective optimization integrating open angle based congestion control strategy. Acta Automatica Sinica, 2015, 41(6): 1145-1158. DOI:10.16383/j.aas.2015.c140555 (  0) 0) |
| [6] |
Zhang Q F, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2008, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 (  0) 0) |
| [7] |
Cheng R, Jin Y, Olhofer M, et al. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791. DOI:10.1109/TEVC.2016.2519378 (  0) 0) |
| [8] |
Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 (  0) 0) |
| [9] |
Xie Cheng-Wang, Yu Wei-Wei, Guo Hua, et al. DAV-MOEA: A many-objective evolutionary algorithm adopting dynamic angle vector based dominance relation. Chinese Journal of Computers, 2022, 45(2): 317-333. (  0) 0) |
| [10] |
Yu Wei-Wei, Xie Cheng-Wang, Bi Ying-Zhou, et al. Many-objective particle swarm optimization based on adaptive fuzzy dominance. Acta Automatica Sinica, 2018, 44(12): 2278-2289. DOI:10.16383/j.aas.2018.c170573 (  0) 0) |
| [11] |
Li L, Lin Q, Ming Z, et al. An immune-inspired resource allocation strategy for many-objective optimization. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 99: 1-14. DOI:10.1109/TSMC.2022.3221466 (  0) 0) |
| [12] |
Zitzler E, Künzli S. Indicator-based selection in multi-objective search. International Conference on Parallel Problem Solving from Nature. Berlin: Springer, 2004, 3242: 832-842.
(  0) 0) |
| [13] |
Falcón-Cardona J G, Coello Coello C A. Indicator-based multi-objective evolutionary algorithms: A comprehensive survey. ACM Computing Surveys, 2021, 52(2): 1-35. DOI:10.1145/3376916 (  0) 0) |
| [14] |
Hernández Gómez R, Coello Coello C A. MOMBI: A new metaheuristic for many-objective optimization based on the R2 indicator. IEEE Congress on Evolutionary Computation. Piscataway: IEEE, 2013.2488-2495. DOI: 10.1109/CEC.2013.6557868.
(  0) 0) |
| [15] |
Bader J, Zitzler E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary Computation, 2011, 19(1): 45-76. DOI:10.1162/EVCO_a_00009 (  0) 0) |
| [16] |
Sun Y, Yen G G, Yi Z. IGD Indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Transactions on Evolutionary Computation, 2019, 23(2): 173-187. DOI:10.1109/TEVC.2018.2791283 (  0) 0) |
| [17] |
Knowles J D, Corne D. Properties of an adaptive archiving algorithm for storing nondominated vectors. Applications of Evolutionary Computation. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 100-116. DOI:10.1109/TEVC.2003.810755 (  0) 0) |
| [18] |
Phan D H, Suzuki J. R2-IBEA: R2 Indicator-based evolutionary algorithm for multi-objective optimization. IEEE Congress on Evolutionary Computation. Piscataway: IEEE, 2013.1836-1845. DOI: 10.1109/CEC.2013.6557783.
(  0) 0) |
| [19] |
Tian Y, Cheng R, Zhang X, et al. An Indicator-based multi-objective evolutionary algorithm with reference point adaptation for better versatility. IEEE Transactions on Evolutionary Computation, 2018, 22(4): 609-622. DOI:10.1109/TEVC.2017.2749619 (  0) 0) |
| [20] |
Deb K, Sindhya K, Okabe T. Self-adaptive simulated binary crossover for real-parameter optimization. Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2007. 1187-1194. DOI: 10.1145/1276958.1277190.
(  0) 0) |
| [21] |
Deb K, Goyal M. A combined genetic adaptive search (GeneAS) for engineering design. Computer Science and Informatics, 1996, 26: 30-45. (  0) 0) |
| [22] |
Hernandez Gomez R, Coello Coello C A. Improved metaheuristic based on the R2 indicator for many-objective optimization. New York: Association for Computing Machinery, 2015: 679-686. DOI:10.1145/2739480.2754776
(  0) 0) |
| [23] |
Liu Y, Gong D, Sun X, et al. Many-objective evolutionary optimization based on reference points. Applied Soft Computing, 2017, 50: 344-355. DOI:10.1016/j.asoc.2016.11.009 (  0) 0) |
| [24] |
Cheng R, Li M, Tian Y, et al. A benchmark test suite for evolutionary many-objective optimization. Complex & Intelligent Systems, 2017, 3(1): 67-81. (  0) 0) |
| [25] |
Bosman P A N, Thierens D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 174-188. DOI:10.1109/TEVC.2003.810761 (  0) 0) |
| [26] |
Zitzler E, Thiele L. Multiobjective evolutionary algorithms: Acomparative case study and the strength Pareto approach. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271. DOI:10.1109/4235.797969 (  0) 0) |
| [27] |
Tian Y, Cheng R, Zhang X, et al. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87. DOI:10.1109/MCI.2017.2742868 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30