2. Shanghai Ship Technology Research Institute, Shanghai 200032, China
Ship painting operation plays a very important role in shipbuilding. According to statistics, in the whole ship construction process, the working hours of the painting operation account for about 12%-18% of the total ship hours[1]. The level of ship painting management is largely reflected in the consumption of paint materials for ship painting and the consumption of working time per unit area of painting[2]. Due to factors such as space restrictions and raw material supply, the previous process of ship block painting is often delayed. Due to the change in the dock loading plan, the delivery time of the subsequent process often needs to be advanced. These two factors make the processing time requirements of the painting operation very strict, so the project completion time becomes the key to the painting schedule.
In the field of scheduling of ship painting, Cho et al.[3] and Kwon et al.[4] proposed heuristic multi-stage methods combined with a mixed integer programming model and priority rules to solve the block painting scheduling problem. Zhang et al. [5] researched the block painting scheduling problem with time and space constraints, but it is difficult to meet the actual scheduling requirements assuming that all blocks are re-entrant only once and the waiting time is the same. Liu and Yao[6] established a hierarchical network planning model for ship block painting production, and used a hybrid genetic algorithm base on a simulated annealing hierarchy to optimize the underlying network planning.
Some researchers regard ship painting as a part of the shipbuilding schedule. Basan et al.[7] introduced a heuristic simulation-based approach to address the scheduling problem for shipbuilding in a real-world multi-stage production system. They explored different types of heuristic rules to reduce the overall production and assembly time of shipbuilding. Liu et al.[8] based on the organizing of the various logistical processes for blocks and the circulation process in the shipyard, established a model that takes the task time window and other factors as constraints to minimize the sum of delay time and no-load time of flat transporters while satisfying the punctuality of scheduling tasks. Finally, the load efficiency can be improved, and the delivery time can be reduced by the optimization model. Tao et al.[9] focused on assembly blocks in shipyards considering precedence and cooperating constraints, and they proposed a metaheuristic algorithm based on the hybrid topological graph and genetic algorithm with tabu search.
In general, the studies on scheduling for ship painting mostly aimed at reducing time or cost. On the other hand, the research on ship block painting operation scheduling always focuses on scheduling each process at the planning level. However, there are few scheduling studies considering the assignment of painting team workers. Although some studies take ship painting as a project scheduling problem considering human resource constraints and propose an effective scheduling method with priority rules[10]. Unfortunately, the study only regards human resources as resource constraints, and fails to consider that painting workers are multi-skilled workers with different efficiency.
For labor-intensive production systems, worker allocation plays a pivotal role in operating efficiency. The skill level of the ship painting workers is uneven, so it is unrealistic to ignore worker heterogeneity. In the analysis of human factors in the field of shipbuilding, operational safety[11], human-computer interaction[12], and the influence of environmental factors [13] are often considered. But in the field of scheduling research, goals such as working hours, total costs, and workload balancing are often focused on[14-15]. Zhu et al. and Zhou et al. aimed at the resource constrained project scheduling problem by considering human resources[16-17]. They allocated the number of workers to maximize profit and used improved meta-heuristic algorithms to solve problems.
For the problem of fine-grained consideration of personnel scheduling, the human factor makes scheduling a particularly difficult optimization problem. Considering the problem scenario of the retail industry[18], Hassani et al. proposed a heuristic staff rescheduling algorithm, which can quickly obtain a Pareto optimal solution between a set of costs and the number of shift changes. For a potash mine scheduling problem, Seifi et al.[19] designed a mixed integer linear program considering the assignment of people and machines under work shifts. They conducted numerical experiments on examples derived from real data. Fang et al.[20] proposed an improved non-dominated sorting genetic algorithm to shorten the production cycle for the problem of worker allocation and balance on the aircraft assembly line. In addition, based on a common management model in actual management, there are also teams considering a multi-agent project staffing problem involving a single project which has to be scheduled under resource constraints[21]. Finally, a bi-evel optimization model is proposed to manage human resources.
After reviewing the above research, it is found that the personnel scheduling problem is limited by the character of the specific problem itself, and mathematical models are often established based on specific production scenarios. As a non-deterministic polynomial difficult problem, its exact solution scale is limited. Therefore, much literature focuses on metaheuristic algorithms. However, due to the previous imperfect information system and extensive management method of the shipyard, few scholars have carried out research on personnel scheduling of ship block painting.
In this paper, a mathematical model is proposed based on the painting production of a shipyard in Shanghai. Based on the model, a path relinking strategy is designed for the painting personnel scheduling model, and an improved scatter search algorithm based on hybrid approximate dynamic programming is proposed. Through the comparison with the GUROBI solver and other algorithms in numerical experiments, the effectiveness of the hybrid algorithm proposed in this paper is verified, which can provide decision support for the process of ship painting production from extensive management to fine management.
1 Elements of Ship Block Painting Operation 1.1 Painting Task Relationship ConstraintsThe tasks of block painting of ships in the spraying workshop can be divided into pre-spraying, spraying, Touch-up, and pump management tasks. The spraying task is the core of the painting operation, and every ship block needs to be further decomposed into more than a dozen working areas. An example of the block working areas is shown in Fig. 1.
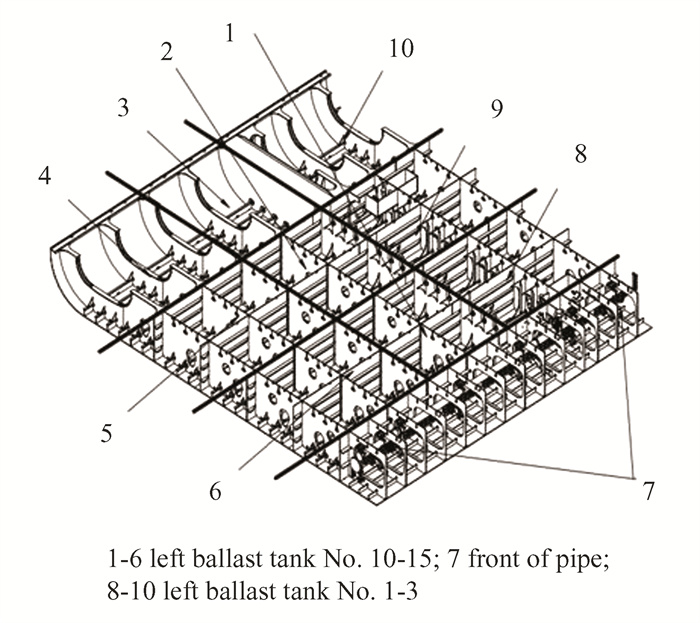
|
Fig.1 Diagram of work areas in a ship block |
Considering the elements involved in the painting process, the constraints between painting tasks include task priority constraints, paint preparation constraints, pump management constraints, and neighbor avoidance constraints.
1.1.1 Task priority constraintsFor the spraying tasks in the work area on the same block, the workers follow the task priority relationship of the space rules: first inside and then outside, first up and then down. In the mathematical model, the task set M ={1, 2, …, m}, i, j∈ M recorded as the task number; the worker set N ={1, 2, …, n}, k∈ N recorded as the worker number; the 0-1 variable xij indicates that there is a priority relationship constraint between tasks, and when xij is 1, it indicates that the task i is the previous priority task of the task j, xij is 0 indicates that the task i is not the previous priority task of the task j.
1.1.2 Paint preparation constraintsThe paint needs to be prepared before it is used in the painting task, and the prepared paint needs to be used up within a certain period, known as the effective service period TES. If the paint required for the task has not been prepared before the task starts, it will take TPP minutes to prepare unified paint according to the sum of the paint task requirements in the next effective service period. In the mathematical model, the value of TPP is 10; the value of TES is 240; pi represents the number of paint required for task i; the 0-1 variable li represents whether paint needs to be prepared at the beginning of task i, li is 1 when the required paint is not prepared at the beginning of task i, and li is 0 indicates that the required paint has been prepared.
1.1.3 Pump management constraintsSince the high-pressure air pump used in the spraying task has safety risks, when a block has a spraying task, there must be a person responsible for checking and monitoring the equipment status, which is called pump management. Denote M′ as the set of pump management tasks, and qi represents the number of the pumping task to which spraying task i belongs.
1.1.4 Neighbor avoidance constraintsTo avoid the interaction of workers spraying on a block simultaneously, spraying tasks in adjacent areas need to be staggered. In the mathematical model, a 0-1 variable zij of 1 indicates that task i and task j are adjacent spraying tasks and cannot be performed at the same time, and a zij of 0 indicates that task i and task j are not adjacent spraying tasks.
1.2 Budget Working Time AnalysisThe shipyard mainly determines the budget working time of various tasks through the base unit time. For the ship painting task, it is necessary to further consider the influence of the difficulty of spraying area, the workers' multi-skills, and the workers' proficiency level.
1) Difficulty of spraying area: according to the functions of ships, ships are usually divided into various areas such as the flat bottom, straight bottom, open deck, freeboard, fore and aft peak tanks, ballast tanks, etc. According to the functions of ships, the regional difficulty coefficient of spraying task i is recorded as Di.
2) Multi-skilled workers: The types of painting tasks in the spraying workshop include 6 different types of spraying tasks, which are deck and hull, ship cabin, bow and stern, ship piping, superstructure, and other settings according to the spray area. After additionally considering pre-spraying, Touch-up, and pump management, there are 9 types of tasks. In the mathematical model, when the 0-1 variable rki is 1, it means that worker k can undertake task i, and when rki is 0, it means that worker k cannot undertake task i.
3) Worker proficiency level: The worker's efficiency coefficient corresponding to the proficiency level will affect the working time. In the mathematical model, the skills mastered by workers are summarized into 5 different proficiency levels, and the proficiency levels 1 to 5 correspond to efficiency coefficients ranging from 1 to 0.6. Denote Rki as the efficiency coefficient of worker k on task i.
To sum it up, calculate the budget working time. For the ship painting task, the operating area Ai of task i is an indicator of the amount of workload completed by the worker, which directly determines the time required for the task. Considering the influence of the painting area's difficulty, the workers' multi-skills, and the workers' efficiency coefficient. The calculation formula of the budget working time in minutes is:
| $ T_{k i}=\left\{\begin{array}{l} H \cdot D_i \cdot R_{k i} \cdot A_i, r_{k i}=1 \\ \text { Inf, }\;\;\;\;\quad\quad\quad\quad r_{k i}=0 \end{array}\right. $ | (1) |
In Eq. (1), Tki represents the time required for worker k to complete task i. H represents the basic unit time, which is set as 0.76 min/m2 according to the production experience in the practice of the shipyard. Before modeling the block painting problem, the budget working time of each worker for each task is obtained by pre-calculation.
2 Painting Personnel Scheduling ModelBased on the known block painting tasks that the team needs to undertake in today's plan and the information on the team's attendance today, the spraying task of each block is divided into the smallest unit tasks. The minimum completion time is the target to complete the scheduling of personnel and tasks. Scheduling decisions focus on intraday planning. While shipyards employ a long-term worker team, the model does not need to consider the cost impact of hiring and firing workers in long-term planning.
In the model, d is used to represent the discrete-time in minutes, and the decision variables are introduced as follows: ti represents the actual time required to complete task i in a specific plan; 0-1 decision variable yki is 1 indicating that worker k undertakes task i, which is 0 means that worker k does not undertake task i; the start time of task i is si and the end time is ci; the completion time of worker k is uk. By reasonably arranging the task allocation and scheduling of workers, the target is to minimize the total completion time U.
The constraints in the mathematical model are as follows:
| $ \text { Obj: } \operatorname{Min} U=\max \left(u_1, u_2, \cdots, u_n\right) $ | (2) |
| $ \sum\limits_{k=1}^n y_{k i}=1, \forall i \in M $ | (3) |
| $ y_{k i} \leqslant r_{k i}, \forall k \in N, i \in M $ | (4) |
| $ t_i=\sum\limits_{k=1}^n T_{k i} \cdot y_{k i}, \forall i \in M / M^{\prime} $ | (5) |
| $ s_i \geqslant 0, \forall i \in M $ | (6) |
| $ c_i \geqslant s_i+t_i+T^{\mathrm{PP}} \cdot l_i, \forall i \in M / M^{\prime} $ | (7) |
| $ s_j \geqslant x_{i j} \cdot c_i, \forall i, j \in M / M^{\prime} $ | (8) |
| $ \begin{gathered} l_j \leqslant\left\{\begin{array}{l} 0, s_j-s_i \geqslant 0 \cap c_j-s_i \geqslant T^\mathrm{ E S} \\ 1, \text { others } \end{array}\right. \\ \;\;\;\;\;\;\;\;\;\;\;\forall i, j \in M, l_i=1, p_i=p_j \end{gathered} $ | (9) |
| $ s_i \leqslant s_j, \forall i \in M^{\prime}, q_j=i $ | (10) |
| $ c_i \geqslant c_j, \forall i \in M^{\prime}, q_j=i $ | (11) |
| $ v_{k i d}=\left\{\begin{array}{l} 1, s_i \leqslant d \leqslant c_i \\ 0, \text { others } \end{array}, \forall y_{k i}=1, k \in N, i \in M\right. $ | (12) |
| $ \sum\limits_{i=1}^m v_{\text {kid }} \leqslant 1, \forall k \in N, d \in\left\{1, \cdots, D_{\max }\right\} $ | (13) |
| $ u_k=\max \left(y_{k 1} \cdot c_1, \cdots, y_{k n} \cdot c_n\right), \forall k \in N $ | (14) |
| $ \begin{gathered} \sum\limits_{k=1}^n V_{k i d}+\sum\limits_{k=1}^n V_{k j d} \leqslant 1, \\ \forall d \in\left\{1, \cdots, D_{\max }\right\}, z_{i j}=1 \end{gathered} $ | (15) |
In this formulation, Constraint (2) indicates that the optimization objective is the minimum total completion time; Constraint (3) indicates that each task can only be assigned to one worker; Constraint(4) indicates that a worker can only perform the tasks that master multi-skill set; Constraints (5)-(7) represent the constraints of the start time, and end time of each task. If the paint needs to be prepared, it will consume an additional time TPP; Constraint (8) represents the priority relationship between tasks; Constraint (9) defines whether the required paint needs to be prepared at the beginning of task j; Constraints (10)-(11) indicate that during the execution of the spraying task, the block to which it belongs must have a worker in charge of the pump task; Constraint (12) represents whether it is undertaken by worker k for task i at time d; Constraint (13) indicates that each worker can only undertake one task at the same time; Constraint(14) indicates the relationship between the completion time of worker k and the end time of tasks the worker is responsible for; Constraint (15) indicates the adjacent spraying tasks cannot be performed simultaneously.
3 Improved Scatter Search AlgorithmThe scatter search (SS) algorithm is a heuristic-based evolutionary algorithm that has been successfully applied to various optimization problems. It has been researched and applied in workshop scheduling problems and vehicle routing problems considering personnel scheduling factors, and it is considered an effective method to solve complex combinatorial optimization problems[22].
The most obvious difference between SS and other evolutionary algorithms is that its operation strategies are not based on the principle of randomness and are more focused on adopting systematic methods to construct new solutions[23]. A scatter search algorithm usually consists of five systematic sub-methods. 1) Generation method of initial solution set is used to generate a large number of different solutions in the initial stage. 2) Reference set (RefSet) update method aims to select solutions with good quality and diversity. 3) Subset generation method generates reference subsets from the solution reference set in each iteration. 4) Combination operator of solutions method generates one or more new solutions from subsets of solutions. 5) Solution improvement method is applied to each newly generated solution.
This paper proposes an improved scatter search (ISS) algorithm. An approximate dynamic programming (ADP) algorithm is introduced in the generation method of initial solution set, which generates diverse solutions to speed up the ISS convergence speed. In combination operator of solutions method, the path relinking solution combination and the task sequence solution combination are proposed. Thus two solution combination methods jointly enhance the breadth of the ISS search space.
The algorithm framework flowchart of the improved scatter search algorithm is shown in Fig. 2. In the initial stage, Psize random task sequences are generated, and the approximate dynamic programming algorithm is executed for each task sequence to obtain Psize solutions as the reference set P. Then two reference subsets are obtained according to the subset generation method. The reference subset RS1 stores high-quality solutions on the basis of ensuring a certain diversity, while RS2 stores more diverse solutions.
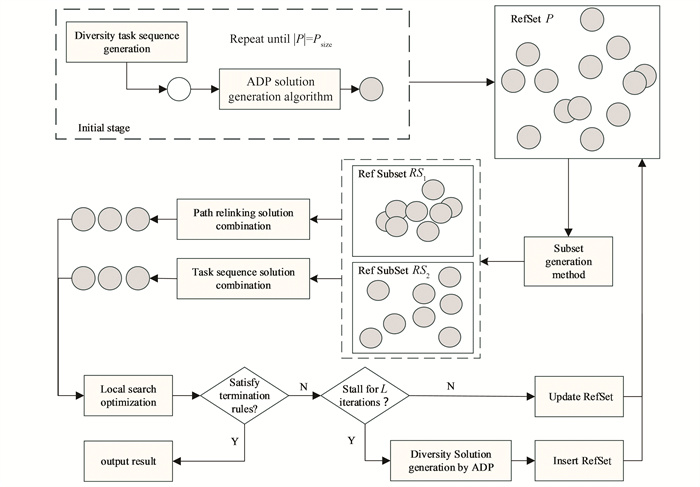
|
Fig.2 Flow chart of the improved scatter search algorithm framework |
Then, two solutions are taken from each of the two subsets for combination. Two combination methods are used here: the path relinking solution combination method is more inclined to the depth of the search, while the task sequence combination method is more inclined to the breadth of the search. Local search is performed for all new solutions obtained by combining them to optimize the model. The subsets RS1 and RS2 are updated with the newly obtained solutions until the termination rules are satisfied. If a better solution cannot be found for a long time, the algorithm will insert the diverse solutions obtained through random sequences into the reference set to avoid the search being trapped in the locality.
The process of the improved scatter search is shown in Algorithm 1, the components of improved scatter search will be explained in detail as follows.
Algorithm 1 ISS algorithm
Input: task data, worker data, Psize
Output: Sbest
1:
Generate Psize random task sequences
2:
Get initialization RefSet P by task sequence (Algorithm 2)
3:
repeat
4:
Update subsets RS1 and RS2 by P (Algorithm 3)
5:
6:
for
7:
for
8:
Combine S1 and S2 to generate Snew (Algorithm 4)
9:
Combine S1 and S2 to generate Snew' (Algorithm 5)
10:
Local search: Snew and Snew'
11:
12:
if find a better solution then
13:
Update Sbest
14:
if stall for L iterations then
15:
P← random diversity solution
16:
Until termination rules are satisfied
17:
Return Sbest
The results of the plan for the scheduling of ship block painting personnel are represented by a two-dimensional sequence of S=(ρ, π). In the personnel assignment sequence ρ=(ρ1, …, ρm), ρi represents which worker is responsible for the task number i; In the task sequence π=(π1, …, πm), πi represents the number of the i task sorted by the task start time.
Due to the NP-hard of the personnel scheduling problem and the problem scale requirement of the exact solution, an approximate dynamic programming algorithm is proposed, which can quickly obtain the approximate optimal solution under the determined task sequence. The algorithm divides the input task sequence π into stages according to the number of tasks, starting from the task sequence length of 1, and recursively obtains the approximate optimal solution in the final stage. This algorithm retains most Fmax solutions at each stage, and uses a scoring function to compare worker completion time set of current solution U′=(u′1, u′2, …, u′n) and each reserved solution Ui, retains the plan with the higher score after comparison.
| $ \begin{gathered} f\left(U^{\prime}, U^i\right)=\alpha \cdot \operatorname{Dom}\left(U^{\prime}, U^i\right)+\beta \cdot\left(\max \left(U^{\prime}\right)-\right. \\ U)^{-}+\gamma \cdot \operatorname{Loss}\left(U^{\prime}\right)^{-} \end{gathered} $ | (16) |
The scoring function is shown in Eq.(16), which includes three factors: the dominating number judgment function Dom, the shortest completion time excess value, and the invalid time function Loss, which replaces the full domination judgment for solving the completion time set in the dynamic programming algorithm. The dominance number refers to the number of workers whose completion time in plan U′ is less than that in plan Ui. After normalizing the factors, the parameter settings are exhaustively exhausted by grid search, and the optimal weight parameter setting is determined as: (α, β, γ)=(0.6, 0.3, 0.1). This method quickly obtains the approximate optimal solution under this task sequence, which avoids the problem of dynamic programming algorithm that takes too long time to solve or even fails to obtain the final result due to the explosion of dimensions.
In the generation method of initial solution set, a large number of random task sequences generated in the initialization phase are input into ADP algorithm in turn. A complete and high-quality plan S can be quickly obtained by each task sequence. Finally, a solution set is formed. The flow of the ADP algorithm is shown in Algorithm 2.
Algorithm 2 ADP algorithm
Input: task sequence π
Output: Sa-best
1:
for
2:
Get a new task p in phase i from π
3:
Calculate all possible plans eFi, j based on set eFi-1
4:
for
5:
if eFi, j do not meet constraints then
6:
Delete exFi, j from set exFi
7:
for
8:
Calculate
9:
if Uj better than Ui then
10:
11:
Get Fmax plans set eFi
12:
Calculate U for all plans in eFm
13:
Get the best solution Sa-best
14:
Return Sa-best
The reference subset is created from the reference set. By searching the reference set, two reference subsets RS1 and RS2 are created. RS1 stores high-quality solutions, while RS2 stores solutions with more diversity, where the solution's diversity is judged by the distance function between solutions[24].
For the solution S=(ρ, π) and the solution S′=(ρ′, π′), the distance between the solutions includes the distance between the personnel assignment ρ and ρ′ and the distance between the task sequence π and π′. The distance of the personnel assignment result can be obtained by calculating the similarities and differences of the personnel assigned to each task. The task sequence is a sequence with contextual significance, thus using Kendall's tau coefficient to define the distance between π and π′ as
| $ \left(S, S^{\prime}\right)=\left|\left\{k \mid \rho(k) \neq \rho^{\prime}(k)\right\}\right|+K\left(\pi, \pi^{\prime}\right) $ |
According to the definition of the distance function, first put the high-quality solutions into the reference subset RS1 according to the distance d1, the distance between the solutions in RS1 is at least d1. Then select the reference subset RS2 from the remaining reference set. The distance between the solutions in RS2 are at least d2, and the distance between solutions in RS1 and RS2 are also at least d2. d2>d1 is set to ensure that the solution in RS2 has a higher diversity.
The flow of reference subset generation method is shown in Algorithm 3. When the subset RS2 is not full, the algorithm generates new solutions to ensure the successful construction of the reference subset.
Algorithm 3 Reference subset generation algorithm
Input: P, d1, d2, subset size rs1 and rs2
Output: RS1, RS2.
1:
2:
while
3:
4:
if
5:
6:
7:
while
8:
9:
if minr∈RS1∪RS2d(S2, r)d2 then
10:
11:
if
12:
Fill RS2 by new solutions
13:
Return RS1, RS2
Two solutions are taken from each of the two reference subsets RS1 and RS2 and then are combined. This paper refers to the idea of finding critical paths in the path relinking algorithm of vehicle routing problems[25], and uses the solution representation of S'=(s1, …, sn) to perform path relinking solution combination, where si=(t1, …, tk) represents the order of all tasks that the worker number i is responsible for.
For the two solutions called parent solutions to be combined, one is used as guiding solution, and the other is used as the initiating solution. Starting from the task which has the latest completion time, the consecutive tasks in charge of the same worker on the critical path are called a path block. As shown in Fig. 3, the critical path of the initiating solution is determined according to the principle of block maximization. If there are multiple such critical paths, one is randomly selected. The sequence on the critical path of the initiating solution is exchanged in turn according to the order guided by the guiding solution, so that the task sequence on the initiating path is always closer to the guiding solution. The combined solution is the best feasible solution among the path solutions obtained during the exploration process. Based on the initiating solution in Fig. 3, the flow of path relinking is shown in Fig. 4.
|
Fig.3 Critical path of an initiating solution |
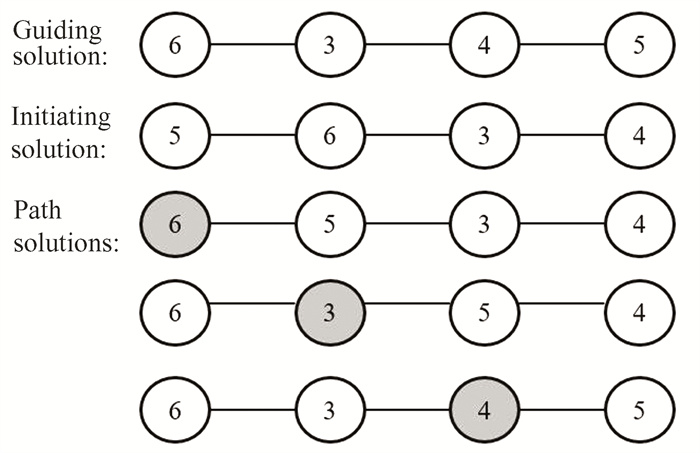
|
Fig.4 Path relinking diagram |
In addition, to the path relinking between the two parent solutions that are mutually guiding solutions and the initiating solution, the path relinking solution combination algorithm also uses the current global optimal solution Sbest as a constant guiding solution. The process relinks each new solution's paths separately and replaces the original solution if a better solution is found. The flow of the path relinking combination algorithm is shown in Algorithm 4.
Algorithm 4 Path relinking combination algorithm
Input: S1, S2, Sbest
Output: Snew
1:
S1 is initiating solution, S2 is guiding solution
2:
Get critical path of S1, get task sequence of S2
3:
while |
4:
5:
Local search: personnel
6:
S2 is initiating solution, S1 is guiding solution
7:
Get critical path of S2, get task sequence of S1
8:
while |
9:
10:
Local search: personnel
11:
Sbest is guiding solution, Snew is initiating solution
12:
if find a better solution then
13:
Replace Snew
14:
Return Snew
Path relinking combination is limited to the critical path in this model, which leads to the localization of the search space. Therefore, the task sequence combination method is used in the construction of new solutions. Considering the task sequences π and π′ of the two parent solutions, randomly obtain a part of the sequence fragments from the sequence π, and then fill in the vacancies according to the sequence π′ to obtain a new task sequence πnew.
An example of the task sequence combination method is shown in Fig. 5.
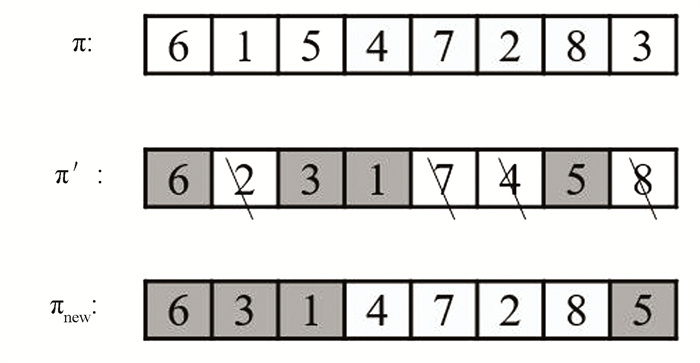
|
Fig.5 Task sequence combination diagram |
The combined task sequence πnew is operated by the ADP algorithm, then the combined solution of the offspring can be obtained. Each iteration obtains h combined solutions in this way. The number of h increases with the number of stagnations of the optimal solution to expand the global nature of your search. The flow of the task sequence combination algorithm is shown in Algorithm 5.
Algorithm 5 Task sequence combination algorithm
Input: S1, S2
Output: Snew
1:
Get task sequences of S1, S2 as π, π′
2:
Get Rand Num: 0 < r1 < r2 < M
3:
4:
while i≤m do:
5:
if i≥r1 and i≤r2 then
6:
7:
else if i≤m then
8:
9:
Get Snew from πnew by Algorithm 2
10:
Return Snew
The local search algorithm is used as the optimization strategy of the solution. For two aspects of personnel assignment and critical task path, 2-opt and 3-opt local searches are carried out. Personnel allocation ensures that the task combination of each person in the original plan remains unchanged, but only the overall exchange between the personnel is carried out. Moreover, the 3-opt local search is applied to all personnel. For the local search method of task critical path, each block on the critical task path is regarded as a simplified neighborhood. 2-opt and 3-opt methods are performed inside each neighborhood. Each newly generated solution is optimized by these two strategies and then enters the reference set.
3.5 Reference Set Update Method and Termination RulesThe reference set P is set as an empty set after each generation of two reference subsets RS1 and RS2. After each iteration, put all the new solutions generated in this iteration into P, and then put the reference subsets RS1 and RS2 into P. If the number of stagnant iterations is greater than L which values 3 in the program, the ADP algorithm generates random solutions with diversity and inserts them into the reference set.
ISS adopts two termination rules. One is the maximum iteration count, which outputs the result and terminates the progress when the number is reached. The other is the maximum stagnation count, which is set to 10 in the program. When the optimal solution cannot be updated for ten consecutive iterations, terminate the algorithm.
4 Numerical ExperimentThis paper uses Matlab 9.2 as the programming environment to carry out numerical experiments on a computer (CPU: Intel Core i9-9940X@3.30GHz; RAM: 16GB; operating system: Window10) to implement the algorithm. In order to verify the effectiveness of ISS, the small scale instances are compared with the optimization solver GUROBI, and the medium and large scale instances are compared with the methods in other literature on personnel scheduling problems. In addition, the ISS solution results were compared and analyzed with the actual production data of the ship block painting.
The numerical experimental data comes from a Shanghai shipyard. On the basis of the normal distribution function of various task times obtained by fitting the actual data and the uniform distribution function of the number of skills mastered by workers, reasonable random tasks and workers' data are generated. Add and delete the test data set with the different number of workers n and tasks m. For small-scale instances (sp101-sp114), this paper sets the scale parameter n×m not more than 12×35; For medium and large scale instances (sp201-sp214), this paper sets the scale parameter n×m not less than 12×40.
4.1 Results of ISS and GUROBI on Small Scale InstancesIn order to verify the effectiveness of the ISS algorithm, the MIP model obtained by linearizing the mathematical model of ship block painting personnel scheduling is solved on small scale instances through the solver GUROBI.
Table 1 shows the results of 14 small scale instances. The completion time (U) unit of the results of the instance is minutes, and the running time (t) unit of the algorithm is seconds. Set the running time upper limit of GUROBI as 7200 s; GAP represents the difference between the optimal solution by GUROBI and the solution by ISS.
| Table 1 Results of ISS and GUROBI on small scale |
The experimental results of small scale numerical examples are shown in Table 1. Most of the results of ISS are the optimal solution with a GAP of 0.0%, and the average GAP is about 0.6%. The GAP is generally kept below 1.9%. With the increase in the size of the instance and the complexity of the problem, GUROBI can not find the optimal solution within the given effective time after the problem size increases to n=12 and m=35, while the ISS algorithm has a maximum operation time of 39.5 s on small scale instances, that showing ISS has obvious advantages in solving efficiency.
4.2 Results of ISS and Other Algorithms on Medium and Large Scale InstancesDue to the little research on personnel scheduling algorithms in the field of ship painting scheduling, this paper draws on an improved scatter search algorithm proposed by Hakli and Ortacay[26], and designs a scatter search algorithm (H-SS) as a comparison algorithm for ship block painting model. Furthermore, a genetic algorithm (S-GA) proposed by Su[27] for personnel task assignment is used for comparison and verification. As shown in Table 2, under the 14 instances of medium and large scale, the unit of completion time of the result is minutes; The optimal solution among three algorithms is marked with an asterisk (*); GAP indicates the difference between the solution of each algorithm and the optimal solution of the three algorithms.
| Table 2 Results of ISS and other algorithms on medium and large scale |
It can be seen from Table 2 that ISS always obtains the relative optimal solution on medium and large scale instances. Compared with H-SS without hybrid approximate dynamic programming algorithm, it can achieve a maximum GAP optimization effect of 3.5% and an average GAP optimization value of 1.5%. Compared with S-GA, the maximum optimization value is 6.0%, and the average is about 3.1%, which verifies the superiority of ISS in solving.
Taking the actual instance sp205 of painting production as an example, then the convergence efficiency of the three algorithms is verified. The results are shown in Fig. 6, and it can be observed that ISS has converged in 25 iterations, which takes 57.8 s; H-SS converges within 40 iterations which takes 58.1 s; S-GA converges within 70 iterations, which takes 179.2 s. ISS has a higher convergence speed than H-SS and S-GA and has a better solution in the initial state. This is because the approximate dynamic programming algorithm finds a large number of high-quality solutions in the initialization phase and increases the subsequent convergence efficiency by the task sequence combination method.
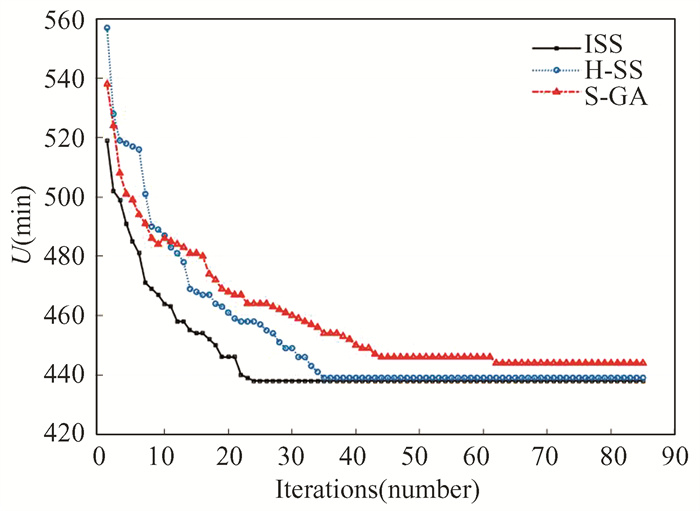
|
Fig.6 Convergence efficiency of different algorithms by iterations |
4.3 Result Analysis of ISS on Production Example
The experimental analysis is carried out by taking the medium and large scale instance sp205 which comes from actual painting production. The proficiency level information of the sp205 workers is shown in Table 3. The proficiency level will be displayed if the worker masters the corresponding skill. Otherwise, the display of the proficiency level will be omitted. The efficiency of the pump management task has nothing to do with the proficiency level, so record that the proficiency level of the worker who masters the pump management skill is 1.
| Table 3 Worker proficiency level of instance sp205 |
Given the input of worker information and task information, after the solution of ISS, the result of the instance sp205 from the actual engineering case is shown in Table 4. Under the painting tasks of 7 blocks that the designated team is responsible for, all tasks are assigned to 15 painting workers. Base worker hours represent the time it takes a worker at proficiency level 1 to complete the task. Each task has its own ship block and required paint. The algorithm tries to maximize the overall painting efficiency under each task constraint, such as pump management and paint preparation.
| Table 4 Task data and result information of instance sp205 |
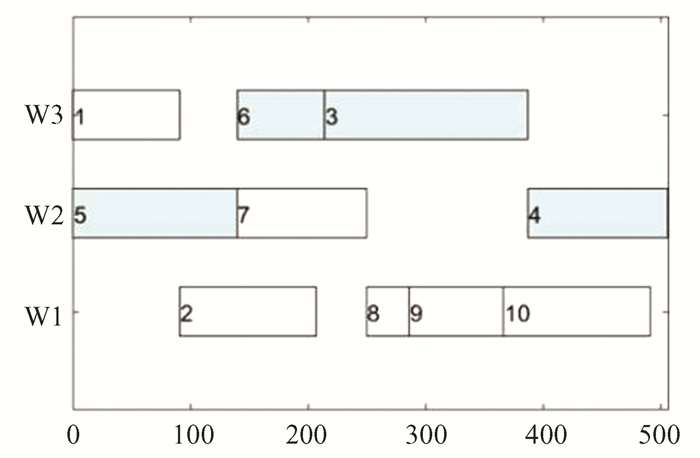
The visualization of solution results of instance sp205 is shown in Fig. 7. Each row represents the task sequence and time arrangement for which the designated worker is responsible. The task color blocks use different colors to represent different task types and paint preparation.
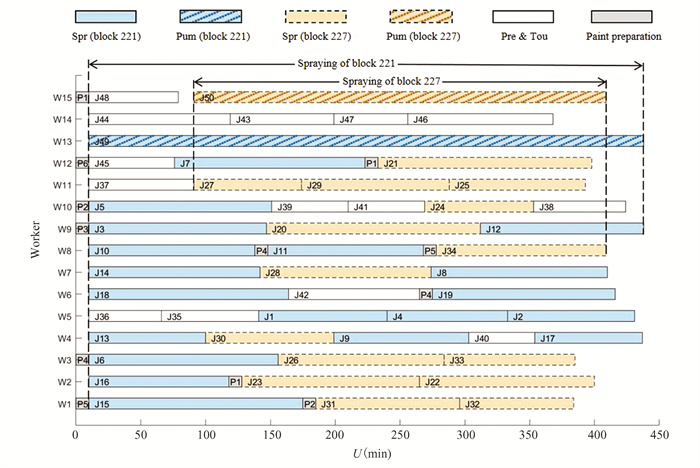
|
Fig.7 Solution result of the instance sp205 |
The output plan was obtained by ISS algorithm. The final completion time of the plan was 438 min, which was 10.61% less than the actual production time of 490 min recorded in the MES system of the shipyard.
Experiments were conducted on the parameter settings of d1 and d2 in reference subset generation method under the instance scale of m=50. The grid search method was used for parameter enumeration, with the parameter range of d1 from 20 to 50 and the parameter range of d2 from 5 to 45. The minimum unit of parameter is 5. Each parameter setting was averaged over 10 instances. Fig. 8 shows the visualization of the grid search results for d1 and d2, where the score represents the completion time under the best parameter setting divided by the completion time under the corresponding parameter setting. A score closer to 1 indicates a better parameter setting. Based on the results of the parameter experiments, the parameter settings of (d1, d2)=(25, 40) were selected and applied to instances of different scales with the parameter settings of (d1, d2)=(0.5 m, 0.8 m).
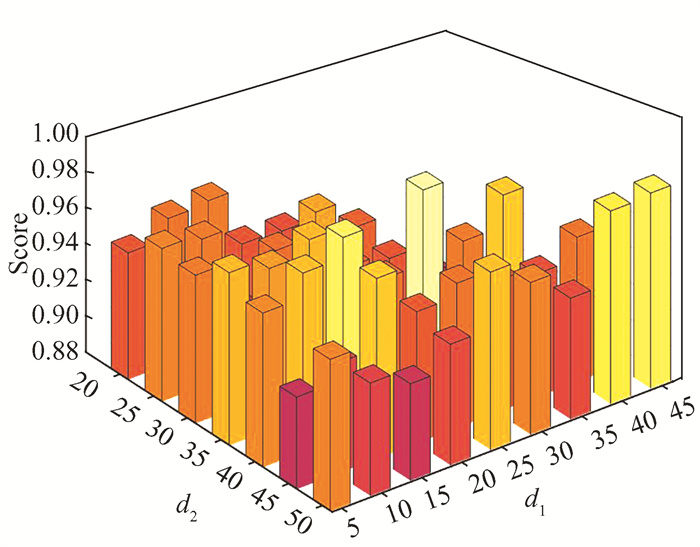
|
Fig.8 Visualization of the grid search for d1 and d2 |
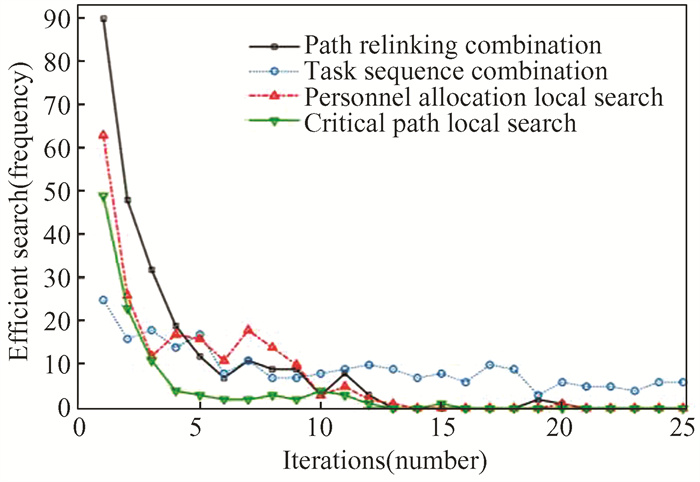
Fig. 9 shows the change of the better solution found times by the two solutions combination strategies and the two local search strategies, which are called during the solution process of the ISS in the instance sp205 with iteration. The search that finds a better solution is called an efficient search. It can be observed that for the local optimization strategy, the critical path local search strategy stalls earlier than the personnel allocation local search strategy. For the solution combination strategy, the path relinking combination strategy efficiently finds the better solution at the beginning of the iteration, while in the later period of iteration, the better solution cannot be found for a long time. However, the task sequence combination strategy stably finds the better solution in the full iteration cycle, which shows that it has a more global search capability.
|
Fig.9 Effects of different strategies in ISS to optimize by iterations |
5 Conclusions
In view of the current situation that the scheduling research in the field of ship painting lacks consideration of personnel factors, this paper takes the personnel scheduling problem of ship block painting as the research object, establishes a mathematical model considering the constraints of actual production scenarios, and designs an improved scatter search algorithm to solve it. Conclusions are summarized as follows:
1) Analyze the elements of the painting operation and summarize the constraints like paint preparation and pump management. Propose a working time Pre-calculation method that considers workers' skill set and proficiency level, then establish a painting personnel scheduling model to minimize the total completion time.
2) An improved scatter search algorithm is proposed to solve this model. The approximate dynamic programming algorithm is used in the two stages of initial solution generation and solution combination, which improve search efficiency. Two solution combination methods, path relinking combination and task sequence combination, are designed to increase the search space.
3) Numerical experiments are carried out based on the data of a large shipyard in Shanghai. For small scale instances, the optimal solution difference between ISS and the GUROBI is about only 0.6%, and ISS has obvious time advantages. Compared with genetic algorithm and other scatter search algorithms in recent literature, the optimization effect can be improved by 3.2% and 1.5% respectively. That verifies the effectiveness and advantages of the proposed algorithm.
4) Run this algorithm on the actual production case of painting to get a schedule plan that shortens the completion time by 10.61%. The result obtained by ISS meets the needs of actual production scheduling, and has guidance and reference for painting plan management from weekly planning to daily refined dispatching workers.
5) Future work will be focused on long-term planning and employment relationship of painting, and the work of this paper will be further extended to a multi-objective optimization problem considering personnel cost and task completion period.
AcknowledgementThe data comes from Shanghai Waigaoqiao Shipyard.
| [1] |
Tang J, Zhao H. Research on comprehensive evaluation system of fine management effect of shipyard painting operation. China Water Transport, 2018, 18(1): 38-40, 74. (in Chinese) (  0) 0) |
| [2] |
Ding C L. The present situation analysis and improvement research of ship painting design and site management. Marine Technology, 2016(1): 80-86. DOI:10.3969/j.issn.1000-3878.2016.01.017 (  0) 0) |
| [3] |
Cho K K, Chuang K H, Park C, et al. A spatial scheduling system for block painting process in shipbuilding. CIRP Annals-Manufacturing Technology, 2001, 50(1): 339-342. DOI:10.1016/S0007-8506(07)62135-0 (  0) 0) |
| [4] |
Kwon B, Lee G M. Spatial scheduling for large assembly blocks in shipbuilding. Computers & Industrial Engineering, 2015, 89: 203-212. DOI:10.1016/j.cie.2015.04.036 (  0) 0) |
| [5] |
Zhang Z Y, Lin C, Yang S, et al. Block-painting-operation-oriented hybrid flow shop scheduling. Journal of Shanghai Jiaotong University, 2014, 48(3): 382-387. DOI:10.16183/j.cnki.jsjtu.2014.03.013 (  0) 0) |
| [6] |
Liu T, Yao Z R. Optimization of parallel construction scheduling on ship block coating. Marine Technology, 2019, 347(1): 82-93. (in Chinese) (  0) 0) |
| [7] |
Basan N P, Achkar V G, Mendez C A, et al. A heuristic simulation-based framework to improve the scheduling of blocks assembly and the production process in shipbuilding. Proceedings of the 2017 Winter Simulation Conference (WSC). Piscataway: IEEE, 2017. 3218-3229. DOI: 10.1109/WSC.2017.8248040.
(  0) 0) |
| [8] |
Liu J, Yin J, Khan R U. Scheduling management and optimization analysis of intermediate products transfer in a shipyard for cruise ships. Plos One, 2022, 17(3): e0265047. DOI:10.1371/journal.pone.0265047 (  0) 0) |
| [9] |
Tao N R, Jiang Z H, Liu J F, et al. A metaheuristic algorithm to transporter scheduling for assembly blocks in a shipyard considering precedence and cooperating constraints. Discrete Dynamics in Nature and Society, 2019(1): 1-14. DOI:10.1155/2019/2615154 (  0) 0) |
| [10] |
Fundeling C U, Trautmann N. A priority-rule method for project scheduling with work-content constraints. European Journal of Operational Research, 2010, 203(3): 568-574. DOI:10.1016/j.ejor.2009.09.019 (  0) 0) |
| [11] |
Oraith H, Blanco-Davis E, Yang Z, et al. An evaluation of the effects of human factors on pilotage operations safety. Journal of Marine Science and Application, 2021, 20(3): 393-409. DOI:10.1007/s11804-021-00222-1 (  0) 0) |
| [12] |
Kari R, Steinert M. Human factor issues in remote ship operations: Lesson learned by studying different domains. Journal of Marine Science and Engineering, 2021, 9(4): 385. DOI:10.3390/jmse9040385 (  0) 0) |
| [13] |
Xue J, Chen Z, Papadimitriou E, et al. Influence of environmental factors on human-like decision-making for intelligent ship. Ocean Engineering, 2019, 186: 106060. DOI:10.1016/j.oceaneng.2019.05.042 (  0) 0) |
| [14] |
Van den Bergh J, Beliën J, De Bruecker P, et al. Personnel scheduling: A literature review. European Journal of Operational Research, 2013, 226(3): 367-385. DOI:10.1016/j.ejor.2012.11.029 (  0) 0) |
| [15] |
Khalfay A, Crispin A, Crockett Keeley A. A review of technician and task scheduling problems, datasets and solution approaches. Proceedings of the 2017 Intelligent Systems Conference (IntelliSys). Piscataway: IEEE, 2017. 288-296. DOI: 10.1109/IntelliSys.2017.8324306.
(  0) 0) |
| [16] |
Zhu H W, Lu Z Q. Modeling and optimization of resource constrained project scheduling problem considering employee-timetabling. Journal of Shanghai Jiaotong University, 2020, 54(6): 624-635. (in Chinese) DOI:10.16183/j.cnki.jsjtu.2018.134 (  0) 0) |
| [17] |
Zhou X Y, Tu Y, Lev B. Production and work force assignment problem: A bi-level programming approach. International Journal of Management Science & Engineering Management, 2015, 10(1): 50-61. DOI:10.1080/17509653.2014.950713 (  0) 0) |
| [18] |
Hassani R, Desaulniers G, Elhallaoui I. Real-time bi-objective personnel rescheduling in the retail industry. European Journal of Operational Research, 2021, 293(1): 93-108. DOI:10.1016/j.ejor.2020.12.013 (  0) 0) |
| [19] |
Seifi C, Schulze M, Zimmerman J. A new mathematical formulation for a potash-mine shift scheduling problem with a simultaneous assignment of machines and workers. European Journal of Operational Research, 2021, 292(1): 27-42. DOI:10.1016/j.ejor.2020.10.007 (  0) 0) |
| [20] |
Fang P C, Yang J-J, Liao Q M, et al. Flexible worker allocation in aircraft final assembly line using multi-objective evolutionary algorithms. IEEE Transactions on Industrial Informatics, 2021, 17(11): 7468-7478. DOI:10.1109/TII.2021.3051896 (  0) 0) |
| [21] |
Milička P, Šůcha P, Vanhoucke M, et al. The bilevel optimisation of a multi-agent project scheduling and staffing problem. European Journal of Operational Research, 2022, 296(1): 72-86. DOI:10.1016/j.ejor.2021.03.028 (  0) 0) |
| [22] |
Fan K, Wang M, Zhai Y, et al. Scatter search algorithm for the multiprocessor task job-shop scheduling problem. Computers & Industrial Engineering, 2019, 127: 677-686. DOI:10.1016/j.cie.2018.11.006 (  0) 0) |
| [23] |
Guo X, Zhou M, Liu S, et al. Lexicographic multi-objective scatter search for the optimization of sequence-dependent selective disassembly subject to multiresource constraints. IEEE Transactions on Cybernetics, 2019, 50(7): 3307-3317. DOI:10.1109/TCYB.2019.2901834 (  0) 0) |
| [24] |
Benavides A J, Ritt M, Miralles C. Flow shop scheduling with heterogeneous workers. European Journal of Operational Research, 2014, 237(2): 713-720. DOI:10.1016/j.ejor.2014.02.012 (  0) 0) |
| [25] |
Li X, Tian P, Aneia Y P. An adaptive memory programming metaheuristic for the heterogeneous fixed fleet vehicle routing problem. Transportation Research Part E: Logistics and Transportation Review, 2010, 46.6: 1111-1127. DOI: 10.1016/j.tre.2010.02.004.
(  0) 0) |
| [26] |
Hakli H, Ortacay Z. An improved scatter search algorithm for the un-capacitated facility location problem. Computers & Industrial Engineering, 2019, 135: 855-867. DOI:10.1016/j.cie.2019.06.060 (  0) 0) |
| [27] |
Su B, Xie N, Yang Y. Hybrid genetic algorithm based on bin packing strategy for the unrelated parallel workgroup scheduling problem. Journal of Intelligent Manufacturing, 2021, 32(4): 957-969. DOI:10.1007/s10845-020-01597-8 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


