As well known, a fatigue life assessment of metals is usually divided into two types: low cycle fatigue (LCF)and medium/high cycle fatigue (HCF). Concerning HCF fatigue assessment, the Wöhler Curve Method is usually used. The Modified Wöhler Curve Method proposed by Susmel and Lazzarin [1], for example, is used to perform the HCF assessment of metals for conventional mechanical components subjected to multiaxial fatigue loading. While for LCF of metals, no doubt, the Coffin-Manson Curve Method is used to perform fatigue life assessment. The Modified Manson-Coffin Curve Method by Susmel et al.[2], for example, is employed to evaluate LCF lifetime of metals under multiaxial fatigue loading.
A key to fatigue life evaluation of metals is in substance that, on the basis of fatigue test data of metallic specimens and mechanical analyses for those specimens, a proper stress intensity parameter, S, is taken to establish a relationship between the stress intensity parameter and the fatigue life, N. For example, the Wöhler Curve Method and the Coffin-Manson Curve Method are two typical examples of the relationship. When a different stress intensity parameter, S, is taken, naturally, a different relationship equation is obtained, which has usually different accuracy and efficiency when to be employed to perform fatigue life assessment. Both accurate and high efficient fatigue life evaluation equation is to be searched for by all field investigators.
Recently, a description on a practicability of the Wöhler Curve Method for low cycle fatigue of metals was given by Yan [3]. By the description and the low cycle fatigue test data of 16MnR steel [4], it is important to show that, for low cycle fatigue of the metallic material, such a way that a stress-based intensity parameter calculated by the linear-elastic analysis is taken to be a stress intensity parameter, S, to establish a relationship between the stress intensity parameter, S, and the fatigue life, N, is practicable. In this work, many metallic materials from the literature are given to show that the Wöhler Curve Method is well suitable for low cycle fatigue analysis of metals.
1 Experimental VerificationsIn order to well show that the Wöhler Curve Method is well suitable for low cycle fatigue analysis of metals, "Uniaxial fatigue assessment according to Manson and Coffin's idea" appearing in Ref.[5] is rewritten as follows:
The strain-based approach postulates that fatigue lifetime can be estimated accurately by simultaneously considering the contributions to fatigue damage of both the elastic and plastic parts of the total strain amplitude (Coffin [6]; Manson [7]; Morrow [8]).
Consider the plain specimen sketched in Fig. 1 and assume that it is subjected to fully reversed uniaxial fatigue loading. According to Basquin's idea[9], the relationship between the stress amplitude, σx, a, and the number of reversals to failure, 2Nf, can be expressed as follows:
| $ \sigma_{x, a}=\sigma_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^b $ | (1) |

|
Fig.1 Plain cylindrical specimen and its gauge length (taken from Ref.[5]) |
where the fatigue strength coefficient σ'f, and the fatigue strength exponent b are material constants to be determined by running appropriate experiments.
By taking full advantage of Eq. (1), it is trivial to calculate the amplitude of the elastic part of the total strain εx, ae, as the number of reversals to failure Nf increases, that is:
| $ \varepsilon_{x, a}^e=\frac{\sigma_{x, a}}{E}=\frac{\sigma'_{\mathrm{f}}}{E}\left(2 N_{\mathrm{f}}\right)^b $ | (2) |
Similarly, the relationship between the plastic strain amplitude, εx, ap, and Nf can be expressed as follows:
| $ \varepsilon_{x, a}^p=\varepsilon^{'}_{\mathrm{f}}\left(2 N_{\mathrm{f}}\right)^c $ | (3) |
where the fatigue ductility coefficient ε'f, and the fatigue ductility exponent c, are also material constants to be determined experimentally.
Finally, if the elastic contribution to the overall fatigue damage is added to the corresponding plastic contribution, the relationship between the total strain amplitude εx, a, and the number of reversals to failure can be written directly in the following explicit form:
| $ \varepsilon_{x, a}=\varepsilon_{x, a}^e+\varepsilon_{x, a}^p=\frac{\sigma_{\mathrm{f}}^{\prime}}{E}\left(2 N_{\mathrm{f}}\right)^b+\varepsilon_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^c $ | (4) |
This relationship is usually called the Manson-Coffin equation.
In this paper, Eq. (1) or (2) is called the Basquin's equation.
Here, a comparison of the Wöhler equation with the Basquin's equation is given below:
Eq.(1) is rewritten as:
| $ \lg \left( {{\sigma _{x, a}}} \right) = b\lg \left( {{N_{\rm{f}}}} \right) + \lg \left( {{{\sigma '}_{\rm{f}}}} \right) + b\lg \left( 2 \right) $ | (5) |
Here, the Wöhler equation is usually written as:
| $ \lg \left( {{\sigma _{x, a}}} \right) = {A_1}\lg \left( {{N_{\rm{f}}}} \right) + {C_1} $ | (6) |
Obviously, Eq.(6) is the same as Eq.(1) by letting
| $ A_1=b, \quad C_1=\lg \left(\sigma_{\mathrm{f}}^{'}\right)+b \lg (2) $ | (7) |
By comparing the Wöhler equation with Basquin's equation, thus, it is seen that the Wöhler equation is the same as Basquin's equation expressed in terms of Eq.(1) or (2). Based on the same, it is concluded that, in performing low cycle fatigue analysis of a metallic material by the Manson-Coffin Curve Method, if the relationship between σx, a and Nf is well revealed by the Basquin's Eq. (1), or if the relationship between εx, ae and Nf is well revealed by using the Basquin's Eq. (2), low cycle fatigue analysis of the metallic material can be well calculated by using the Wöhler equation. Here, a metallic material with well linear fitting relationship between lg(σx, a) and lg(Nf) or lg(εx, ae) and lg(Nf) is called the Basquin's material. Obviously, for the Basquin's material, its LCF analysis is well calculated by the Wöhler equation, which will be illustrated by means of the following examples from the literature.
In order to illustrate that the low cycle fatigue life of Basquin's material is to be well predicted by the Wöhler equation, we searched for relevant studies on low cycle fatigue of metals. Here, such studies are divided into three types: Type Ⅰ, Type Ⅱ, and Type Ⅲ.
1.1 Type ⅠBoth low cycle fatigue test data of a metallic material and Strain-life curves obtained by using the Manson-Coffin equation are included in the literature. Then the Basquin's curve in the Strain-life curves is used to show that the metallic material is the Basquin's material, its LCF life is to be well predicted by the Wöhler equation, and at the same time, low cycle fatigue test data of the metallic material are analyzed by using the Wöhler equation to further show that LCF life of the metallic material can be calculated by the Wöhler equation. Such type materials include EN AW-2007 aluminum alloy[10] and EN AW-2024-T3 aluminum alloy[11].
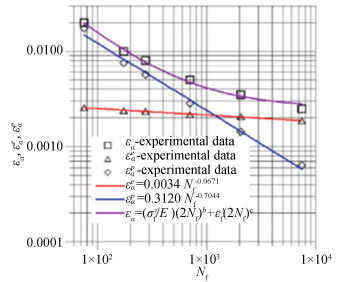
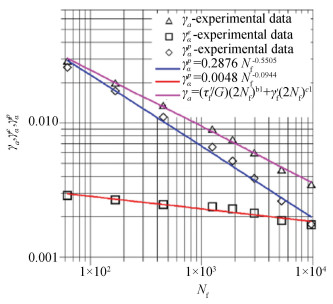
1.1.1 Example 1: Low cycle fatigue of EN AW-2007 aluminum alloyHere, low cycle fatigue test data (see Table 1 and Table 2) of EN AW-2007 aluminum alloy reported by Szusta and Seweryn [10] is employed to show that, for the Basquin's material, its low cycle fatigue life is to be well predicted by the Wöhler Curve Method. Figs. 2, 3 and 4 illustrate the monotonic tension curve, the fatigue life strain curve for the symmetrical tension-compression, the fatigue life curve for symmetrical torsion, respectively. From Figs. 3 and 4, it can be seen that low cycle fatigue life of the metallic material is characterized by using the Manson-Coffin equation, and that low cycle fatigue life of the metallic material is characterized also by the Basquin's equation because the relationship between εae and Nf is well described by Basquin's equation. Thus the metallic material is the Basquin's material.
| Table 1 Low cycle fatigue test data of EN AW-2007 aluminum alloy (for tension R=-1) and predicted results by Wöhler Curve Method |
| Table 2 Low cycle fatigue test data of EN AW-2007 aluminum alloy(for torsion R =-1) and predicted results by Wöhler Curve Method |

|
Fig.2 Tension curve of EN AW-2007 alloy (Taken from Ref.[10]) |
|
Fig.3 Low cycle fatigue life strain curve of EN AW-2007 alloy for the symmetrical tension-compression (Taken from Ref.[10]) |
|
Fig.4 Low cycle fatigue life curve for EN AW-2007 alloy for symmetrical torsion (Taken from Ref.[10]) |
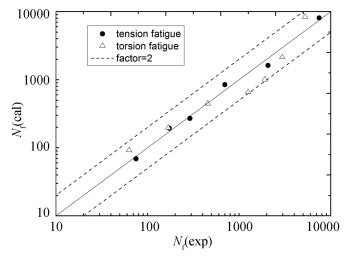
Here, an attempt is made that the Wöhler Curve Method is employed to analyze low cycle fatigue test data of EN AW-2007 aluminum alloy. The obtained results are given in Tables 1-3 and Fig. 5. From Fig. 5, it can be seen that the test fatigue lives are in good agreement with those predicted by the Wöhler curve Method, with error indexes : M.E.=1.0%, E.R.=[-21.4, 21.1]%, and M.E.=10.7%, E.R.=[-47.7, 87.8]% for tension and torsion fatigue, respectively. R.E., M.E., and E.R. are the abbreviation of relative error, mean error and range of error, respectively.Thus, it can be concluded that for the Basquin's material, EN AW-2007 aluminum alloy, its low cycle fatigue life is to be well calculated by the Wöhler Curve Method.
| Table 3 Curve fitting constants in Wöhler equation for EN AW-2007 aluminum alloy |
|
Fig.5 Comparison of test fatigue lives with those predicted by Wöhler Curve Method (EN AW-2007 alloy) |
1.1.2 Example 2: Low cycle fatigue of aluminum alloy EN AW-2024-T3
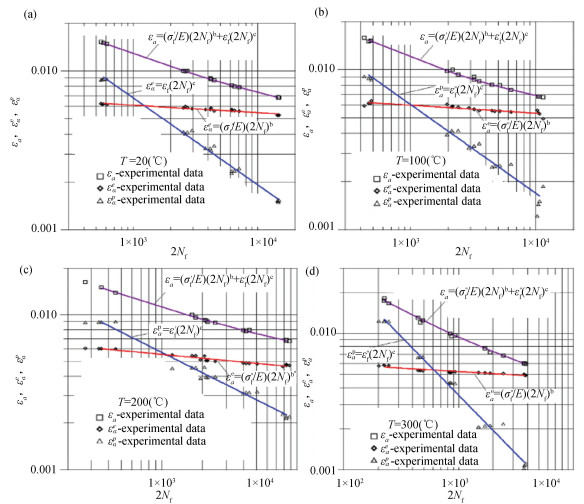
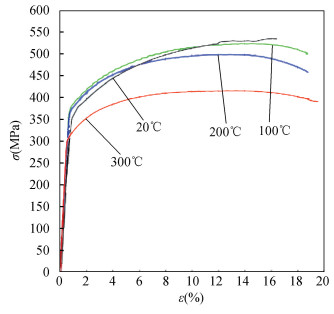
Here, low cycle fatigue test data (as shown in Table 4 and Fig. 6) of aluminum alloy EN AW-2024-T3 at room temperature(RT) and elevated temperature reported by Szusta and Seweryn [11] is employed to further show the author's viewpoint that, for Basquin's material, its low cycle fatigue life is to be well predicted by the Wöhler Curve Method. Fig. 7 is a comparison of monotonic tension curves of EN AW-2024T3 aluminum alloy at 20°, 100°, 200°, 300°.
| Table 4 Low cycle fatigue test data of EN AW-2024-T3 alloy specimens at room temperature (RT) and elevated temperature and the predicted results by using Wöhler Curve Method |
|
Fig.6 Low cycle fatigue life curve for EN AW-2024T3 aluminum alloy samples in the tension loading conditions and temperature of: (a) T=20°, (b) T=100°, (c) T=200°, and (d) T=300° (Taken from Ref.[11]) |
|
Fig.7 A comparison of tension curves of EN AW-2024T3 aluminum alloy at 20°, 100°, 200°, 300° (Taken from Ref.[11]) |
From Fig. 6, it can be seen that low cycle fatigue life of the metallic material is characterized by using the Manson-Coffin curve, and that low cycle fatigue life of the metallic material is characterized also by the Basquin's equation because the relationship between εae and Nf is well expressed by Basquin's equation. Thus the metallic material is Basquin's material.
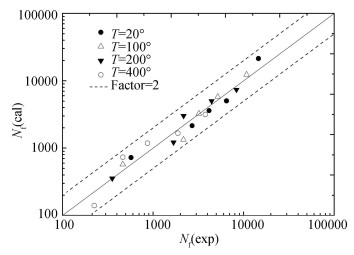
Here, low cycle fatigue test data (see Table 4) of aluminum alloy EN AW-2024-T3 at room temperature (RT) and elevated temperature reported by Szusta and Seweryn [11] are analyzed by using the Wöhler Curve Method. The obtained results are given in Table 4, see also Fig. 8. From Fig. 8, it can be seen that the test fatigue lives are in good agreement with those calculated by the Wöhler Curve Method, with error indexes: M.E.=3.4%, E.R.=[-22.2, 46.2]%; M.E.=2.7%, E.R.=[-38.1, 23.5]%; M.E.=2.5%, E.R.=[-27.5, 38.7]% and M.E.=5.8%, E.R.=[-37.3, 58.2]% for 20°, 100°, 200°, and 300°respectively.
|
Fig.8 Comparison of test fatigue lives with those predicted by Wöhler Curve Method |
Table 5 gives the fitting constants in the Wöhler equation of aluminum alloy EN AW-2024-T3. It can be seen from the various values of R square shown in Table 5 that low cycle fatigue life of the metallic material is well calculated by using the Wöhler Curve Method.
| Table 5 Curve fitting constants in Wöhler equation for aluminum alloy EN AW-2024-T3 |
1.2 Type Ⅱ and Type Ⅲ
Type Ⅱ: Low cycle fatigue test data of a metallic material are given but Strain-life curves are not reported in the literature. Then low cycle fatigue test data of the metallic material are analyzed by using the Wöhler equation to show that low cycle fatigue life of the metallic material can be computed by the Wöhler equation. Such type metals include A533B [12], Inconel 718[13], SAE1045[14], AISI304[15], Ti-6Al-4V[16], 6061-T6[17], 1Cr-18Ni-9Ti[18], AISI304[19], AISIH11[20], 34CrNiMo6[21], RAFM steels [22]. The details are shown in Appendix A.
Type Ⅲ: Strain-life curves of a metallic material are reported but low cycle fatigue test data are not given in the literature. Then the Basquin's curve in the Strain-life curves is used to show that the metallic material is the Basquin's material, its low cycle fatigue life is to be well predicted by Wöhler equation. Such type metallic materials include: P92 ferritic-martensitic steel [23], Cr-Mo-V low alloy steel [24], S35C carbon steel and SCM 435 alloy steel [25-26], high strength spring steel with different heat-treatments [27], 316 L(N) stainless steel at room temperature[28], CLAM steel at room temperature[29]), Eurofer97[30], F82H (a ferritic-martensitic steel)[31], En3B (a commercial cold-rolled low-carbon steel)[32], nodular cast iron[33] and low carbon grey cast iron[34]. The details are reported in Appendix B.
2 Conclusions and Further WorkFrom this work, the conclusions can be made: Wöhler Curve Method is well suitable for LCF life analysis of metallic materials, in which the stress-based intensity parameter calculation is on the basis the linear-elastic analysis without the need for carrying out complex and time-consuming the elastic-plastic analysis.
In view of the fact that medium/high cycle fatigue lives of metallic materials are well calculated by the Wöhler Curve Method, thus, from this work it appears to be possible that the Wöhler Curve Method is well suitable for fatigue life assessment for low/medium/high cycle fatigue of metallic materials. This work will be reported in another paper.
Appendix AExperimental investigations: The Wöhler Curve Method is well suitable for low cycle fatigue life analysis of metals by using low cycle fatigue test data of the metals from the literature.
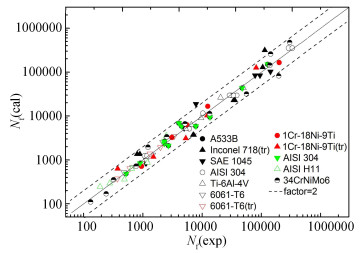
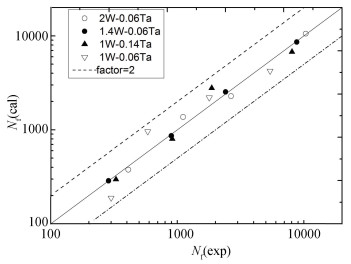
Here, low cycle fatigue test data of metals reported in the literature are analyzed by the Wöhler Curve Method to show that low cycle fatigue life of the metals can be calculated by the Wöhler Curve Method. A summary of the obtained results is given in Table A-1, the test data of different metals and the corresponding results are shown in Tables A-2 to A-14. Comparison of the test low cycle fatigue lives with those calculated by the Wöhler Curve Method are shown in Figs. A-1 and A-2. Such type materials are A533B [12](Table A-2), Inconel 718[13](Table A-3), SAE 1045 [14](Table A-4), AISI 304 [15] (Table A-5), Ti-6Al-4V[16](Table A-6), 6061-T6 [17] (Table A-7, Table A-8), 1Cr-18Ni-9Ti [18] (Table A-9, Table A-10), AISI 304 [19] (Table A-11), AISI H11 [20](Table A-12), 34CrNiMo6[21](Table A-13), RAFM steels [22](Table A-14).
| Table A-1 Summary: low cycle fatigue test data of metals reported in the literature are analyzed by using the Wöhler equation or the Basquin's equation |
| Table A-2 Strain-controlled low cycle fatigue test data of A533B and calculated results by Basquin's equation |
| Table A-3 Strain-controlled low cycle fatigue test data of Inconel 718 and calculated results by Basquin's equation |
| Table A-4 Strain-controlled low cycle fatigue test data of SAE 1045 and calculated results by Basquin's equation |
| Table A-5 Strain-controlled low cycle fatigue test data of AISI 304 and calculated results by Basquin's equation |
| Table A-6 Strain-controlled low cycle fatigue test data of Ti-6Al-4V and calculated results by Wöhler equation |
| Table A-7 Strain-controlled low cycle fatigue test data of 6061-T6 and calculated results by Wöhler equation (tension) |
| Table A-8 Strain-controlled low cycle fatigue test data of 6061-T6 and calculated results by Wöhler equation (torsion) |
| Table A-9 Strain-controlled low cycle fatigue test data of 1Cr-18Ni-9Ti and calculated results by Wöhler equation (tension) |
| Table A-10 Strain-controlled low cycle fatigue test data of 1Cr-18Ni-9Ti and calculated results by Wöhler equation (torsion) |
| Table A-11 Strain-controlled low cycle fatigue test data of AISI 304 and calculated results by Wöhler equation |
| Table A-12 Strain controlled low cycle fatigue testl results of AISI H11 hot-work tool steel and predicted results by using by Wöhler equation |
| Table A-13 low cycle fatigue test data of 34CrNiMo6 high strength steel and predicted results by using by Wöhler equation |
| Table A-14 Low cycle fatigue test data of RAFM steels and predicted results by using Wöhler equation |
|
Fig.A-1 Comparison of low cycle fatigue test lives of metals with those calculated by the Wöhler Curve Method |
|
Fig.A-2 Comparison of low cycle fatigue test lives of AFM steels with those calculated by the Wöhler Curve Method |
From Tables A-1 to A-14 and Figs. A-1 and A-2, it can be seen that the test low cycle fatigue lives of the metals are in good agreement with those calculated by the Wöhler Curve Method, which illustrates that low cycle fatigue life of the metals can be well calculated by the Wöhler Curve Method.
Appendix BExperimental investigations: The Wöhler Curve Method is well suitable for low cycle fatigue life analysis of metals by using the Basquin's curve in the Strain-life curves of metals from the literature.
Here, the Basquin's curve in the Strain-life curves of a metallic material reported in the literature is employed to show that the metallic material is the Basquin's material, its low cycle fatigue life is to be well predicted by the Wöhler Curve Method. Such type materials are P92 ferritic-martensitic steel[23](as shown in Fig.B-1), Cr-Mo-V low alloy steel[24](as shown in Fig.B-2), S35C carbon steel and SCM 435 alloy steel [25-26](as shown in Fig.B-3), high strength spring steel with different heat-treatments[27](as shown in Fig.B-4), 316 L(N) stainless steel at room temperature[28](as shown in Fig.B-5), CLAM steel at room temperature[29])(as shown in Fig.B-6), Eurofer97[30](as shown in Fig.B-7), F82H (a ferritic-martensitic steel)[31](as shown in Fig. B-8), En3B (a commercial cold-rolled low-carbon steel)[32](as shown in Fig.B-9), nodular cast iron[33](as shown in Fig. B-10) and low carbon grey cast iron[34](as shown in Fig. B-11).
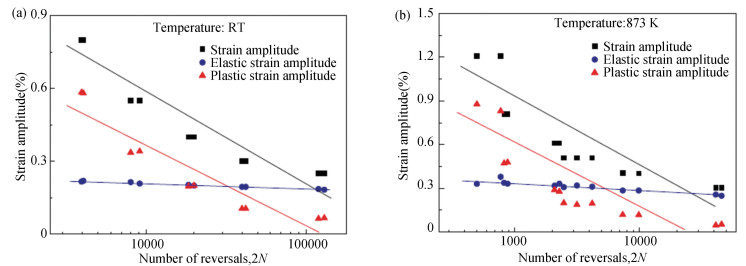
|
Fig.B-1 Strain-life curve of P92 ferritic-martensitic steel (a) RT, (b) 873 K(Taken from Zhang et al.[23]) |
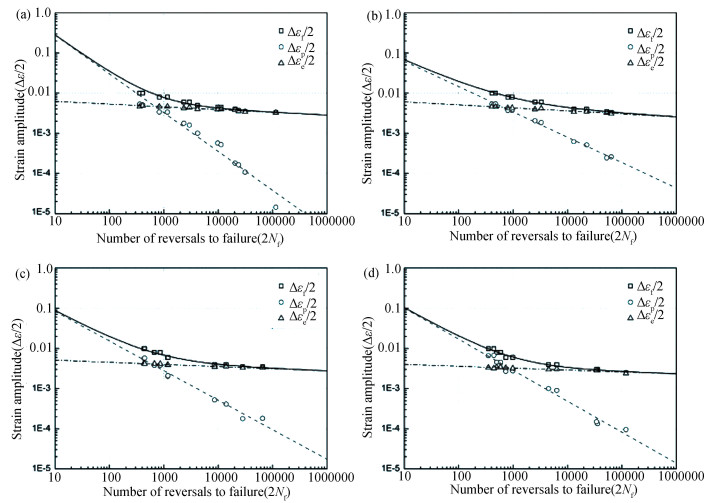
|
Fig.B-2 Strain-life curves of Cr-Mo-V low alloy steel at (a) RT, (b) 200°, (c) 400°, and (d) 600°(Taken from Li [24]) |
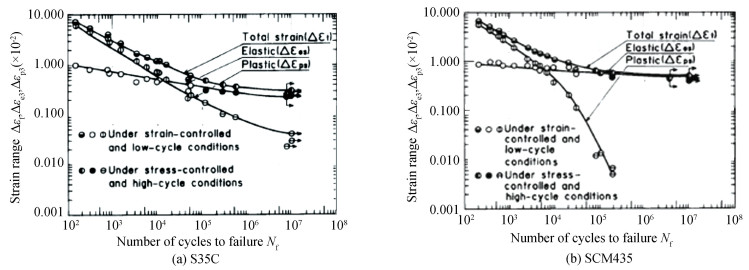
|
Fig.B-3 Strain-life curves S35C carbon steel normalized and SCM 435 alloy steel quenched and then tempered(Taken from Hatanaka[25-26]) |
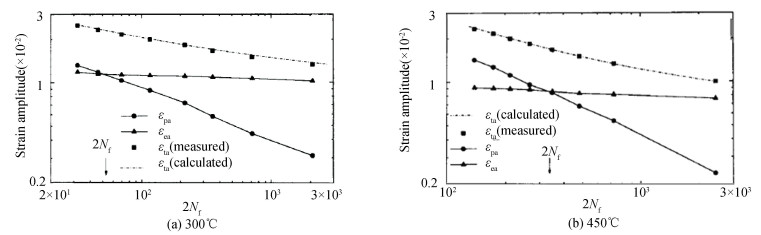
|
Fig.B-4 Strain-life curves of high strength spring steel with different heat-treatments(Taken from Li[27]) |

|
Fig.B-5 Strain-life plots of 316 L(N) stainless steel at room temperature(Taken from Roy[26]) |
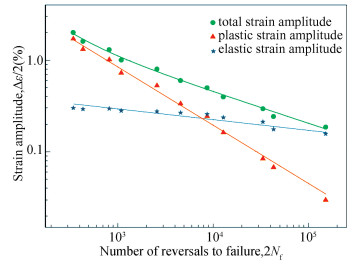
|
Fig.B-6 Strain-life plots CLAM steel at room temperature(Taken from Hu[29]) |
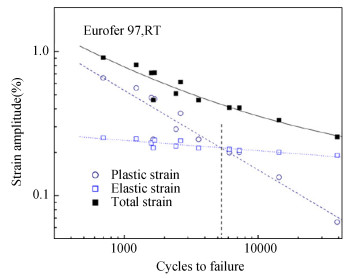
|
Fig.B-7 Strain-life plots of Eurofer 97(Taken from Marmy[30]) |
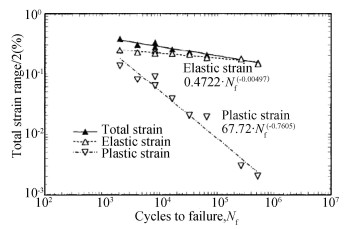
|
Fig.B-8 Strain-life plots of F82H(a ferritic-martensitic steel)(Taken from Stubbins[31]) |
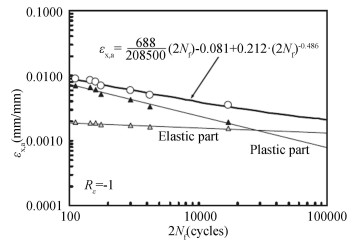
|
Fig.B-9 Strain-life plots of En3B (a commercial cold-rolled low-carbon steel)(Taken from Atzori[32]) |
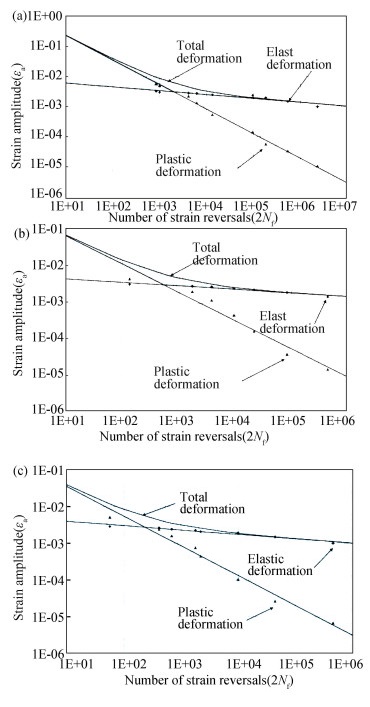
|
Fig.B-10 Strain-life curves of nodular cast iron at (a) RT, (b) 300°, (c) 400°(Taken from Šamec[33]) |
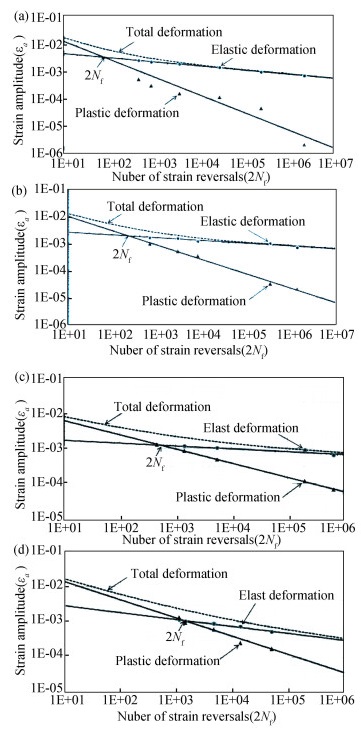
|
Fig.B-11 Strain-life curves of low carbon grey cast iron at (a) RT, (b) 500°, (c) 600° and (d) 700°(Taken from Pevec[34]) |
From Figs. B-1 to B-11, it can be seen that all Basquin's curves have well linear fitting relationship between lg(εx, ae) and lg(Nf). Thus all the metals studied are the Basquin's materials, then their low cycle fatigue lives can be calculated by the Wöhler Curve Method.
From Fig.B-1, it can be seen that there is no well linear fitting relationship between lg(εx, ap) and lg(Nf). So low cycle fatigue life of P92 ferritic-martensitic steel appears to be not well calculated by the Manson-Coffin equation.
From Fig.B-3, it can be seen that, from low-cycle to high-cycle fatigue of the two materials, the relationship between εae and Nf is expressed by the Basquin's equation. Thus it is very possible that the fatigue life of the two materials, from low cycle to high cycle fatigue, is well calculated by the Wöhler Curve Method.
In addition, it can be seen from Fig. B-10 (Strain-life curves of nodular cast iron) that, from low-cycle to high-cycle fatigue of the material at room temperature, the relationship between εae and Nf is expressed by Basquin's equation. Thus it is very possible that the fatigue life of the material at room temperature, from low cycle to high cycle fatigue, is well calculated by the Wöhler equation.
| [1] |
Susmel L, Lazzarin P. A bi-parametric modified Wöhler curve for high cycle multiaxial fatigue assessment. Fatigue and Fracture of Engineering Materials and Structures, 2002, 25: 63-78. DOI:10.1046/J.1460-2695.2002.00462.X (  0) 0) |
| [2] |
Susmel L, Meneghetti G, Atzori B. A simple and efficient reformulation of the classical Manson-Coffin curve to predict lifetime under multiaxial fatigue loading. Part Ⅰ: plain materials. Transactions of the ASME, Journal of Engineering Materials and Technology, 2009, 131(2): 021009. DOI:10.1115/1.3078300 (  0) 0) |
| [3] |
Yan X Q. A local approach for fracture analysis of V-notch specimens under Mode-Ⅰ loading. Engineering Fracture Mechanics, 2022, 274: 108753. DOI:10.1016/j.engfracmech.2022.108753 (  0) 0) |
| [4] |
Gao Z, Zhao T, Wang X, et al. Multiaxial fatigue of 16MnR steel. Journal of Pressure Vessel Technology, 2009, 131(2): 021403. DOI:10.1115/1.3008041 (  0) 0) |
| [5] |
Susmel L. Multiaxial Notch Fatigue, from Nominal to Stress/Strain Quantities. Cambridge: CRC Press, Woodhead Publishing Limited, 2009.
(  0) 0) |
| [6] |
Jr Coffin L F. A study of the effects of cyclic thermal stresses on a ductile metal. Transactions of the ASME, 1954, 76: 931-949. DOI:10.1115/1.4015020 (  0) 0) |
| [7] |
Manson S S. Behaviour of Materials Under Conditions of Thermal Stress. Virginia: National Advisory Committee for Aeronautics, 1954.
(  0) 0) |
| [8] |
Morrow J D. Cyclic plastic strain energy and fatigue of metals. Internal Friction, Damping and Cyclic Plasticity. Philadelphia: American Society for Testing and Materials, 1965: 45-84.
(  0) 0) |
| [9] |
Basquin O H. The exponential law of endurance tests. Proceedings of American Society for Testing and Materials, 1910, 10: 625-630. (  0) 0) |
| [10] |
Szusta J, Seweryn A. Fatigue damage accumulation modeling in the range of complex low-cycle loadings-the strain approach and its experimental verification on the basis of EN AW-2007 aluminum alloy. International Journal of Fatigue, 2011, 33: 255-264. DOI:10.1016/j.ijfatigue.2010.08.013 (  0) 0) |
| [11] |
Szusta J, Seweryn A. Experimental study of the low-cycle fatigue life under multiaxial loading of aluminum alloy EN AW-2024-T3 at elevated temperatures. International Journal of Fatigue, 2016, 96: 28-42. DOI:10.1016/j.ijfatigue.2016.11.009 (  0) 0) |
| [12] |
Nelson D V, Rostami A. Biaxial fatigue of A533B pressure vessel steel. Transactions of the ASME, Journal of Pressure Vessel Technology, 1997, 119: 325-331. DOI:10.1115/1.2842312 (  0) 0) |
| [13] |
Socie D F, Kurath P, Koch J. A multiaxial fatigue damage parameter. Biaxial and Multiaxial Fatigue, EGF 3, edited by M. W. Brown and K. J. Miller. London: Mechanical Engineering Publications, 1989: 535-550.
(  0) 0) |
| [14] |
Kurath P, Downing S D, Galliart D R. Summary of non-hardened notched shaft-round robin program. Multiaxial Fatigue-Analysis and Experiments, edited by G. E. Leese and D. F. Socie, SAE AE-14. Warrendale, PA: Society of Automotive Engineers, 1989: 13-32.
(  0) 0) |
| [15] |
Socie D F. Multiaxial fatigue damage models. Transactions of the ASME, Journal of Engineering Materials and Technology, 1987, 109: 293-298. DOI:10.1115/1.3225980 (  0) 0) |
| [16] |
Kallmeyer A R, Krgo A, Kurath P. Evaluation of multiaxial fatigue life prediction methodologies for Ti-6Al-4V. Transactions of the ASME, Journal of Engineering Materials and Technology, 2002, 124: 229-237. DOI:10.1115/1.1446075 (  0) 0) |
| [17] |
Lin H, Nayeb-Hashemi H, Pelloux R M. Constitutive relations and fatigue life prediction for anisotropic Al-6061-T6 rods under biaxial proportional loadings. International Journal of Fatigue, 1992, 14: 249-259. DOI:10.1016/0142-1123(92)90009-2 (  0) 0) |
| [18] |
Chen X, An K, Kim K S. low-cycle fatigue of 1Cr-18Ni-9Ti stainless steel and related weld metal under axial, torsional and 90 out-of-phase-loading. Fatigue and Fracture of Engineering Materials and Structures, 2004, 27: 439-448. DOI:10.1111/j.1460-2695.2004.00740.x (  0) 0) |
| [19] |
Itoh T, Sakane M, Ohnami M, et al. Nonproportional low cycle fatigue criterion for type 304 stainless steel. Transactions of the ASME, Journal of Engineering Materials and Technology, 1995, 117: 285-292. DOI:10.1115/1.2804541 (  0) 0) |
| [20] |
Du W, Luo Y, Wang Y, et al. A new energy-based method to evaluate low-cycle fatigue damage of AISI H11 at elevated temperature. Fatigue & Fracture Engineering Materials & Structures, 2017, 40: 994-1004. DOI:10.1111/ffe.12570 (  0) 0) |
| [21] |
Branco R, Costa J D, Antunes F V. low-cycle fatigue behavior of 34CrNiMo6 high strength steel. Theoretical and Applied Fracture Mechanics, 2012, 58: 28-34. DOI:10.1016/j.tafmec.2012.02.004 (  0) 0) |
| [22] |
Shankar V, Mariappan K, Nagesha A, et al. Effect of tungsten and tantalum on the low cycle fatigue behavior of reduced activation ferritic/martensitic steels. Fusion Engineering and Design, 2012, 87: 318-324. DOI:10.1016/j.fusengdes.2012.01.020 (  0) 0) |
| [23] |
Zhang Z, Hu Z F, Schmauder S, et al. Low cycle fatigue properties and microstructure of P92 ferritic-martensitic steel at room temperature and 873 K. Materials Characterization, 2019, 157: 109923. DOI:10.1016/j.matchar.2019.109923 (  0) 0) |
| [24] |
Li Z Q, Han J M, Li W J, et al. Low cycle fatigue behavior of Cr-Mo-V low alloy steel used for railway brake discs. Materials and Design, 2014, 56: 146-157. DOI:10.1016/j.matchar.2019.109923 (  0) 0) |
| [25] |
Hatanaka K. Cyclic stress-strain responds and low-cycle fatigue life in metallic materials. International Journal(Series 1), 1990, 33(1): 13-25. (  0) 0) |
| [26] |
Hatanaka K, Fujimisu T. The cyclic stress-strain response and strain life behavior of metallic materials. Proc. of Fatigue '84, 1984, 1: 93. (  0) 0) |
| [27] |
Li D M, Kim K W, Lee C S. Low cycle fatigue data evaluation for a high strength spring steel. Int. J. Fatigue, 1997, 19(8-9): 607-612. DOI:10.1016/S0142-1123(97)00074-1 (  0) 0) |
| [28] |
Roy S C, Goyal S, Sandhy R, et al. Low cycle fatigue life prediction of 316 L(N) stainless steel based on cyclic elasto-plastic response. Nuclear Engineering and Design, 2012, 253: 219-225. DOI:10.1016/j.nucengdes.2012.08.024 (  0) 0) |
| [29] |
Hu X, Huang L X, Wang W G, et al. Low cycle fatigue properties of CLAM steel at room temperature. Fusion Engineering and Design, 2013, 88: 3050-3059. DOI:10.1016/j.fusengdes.2013.08.001 (  0) 0) |
| [30] |
Marmy P, Kruml T. Low cycle fatigue of Eurofer 97. Journal of Nuclear Materials, 2008, 377: 52-58. DOI:10.1016/j.jnucmat.2008.02.054 (  0) 0) |
| [31] |
Stubbins J F, Gelles D S. Fatigue performance and cyclic softening of F82H, a ferritic-martensitic steel. Journal of Nuclear Materials, 1996, 233-237: 33l-335. DOI:10.1016/S0022-3115(96)00226-7 (  0) 0) |
| [32] |
Atzori B, Meneghetti G, Susmel L, et al. The modified Manson-Coffin method to estimate low-cycle fatigue damage in notched cylindrical bars. Proceedings of the 8th International Conference on Multiaxial Fatigue and Fracture. Sheffield: Springer, 2007.
(  0) 0) |
| [33] |
Šamec B, Potrč I, Šraml M. Low cycle fatigue of nodular cast iron used for railway brake discs. Engineering Failure Analysis, 2011, 18: 1424-1434. DOI:10.1016/j.engfailanal.2011.04.002 (  0) 0) |
| [34] |
Pevec M, Oder G, Potrč I, et al. Elevated temperature low cycle fatigue of grey cast iron used for automotive brake discs. Engineering Failure Analysis, 2014, 42: 221-230. DOI:10.1016/j.engfailanal.2014.03.021 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


