2. School of Engineering, Hulunbuir University, Hulun Buir 021008, Inner Mongolia, China;
3. School of Mathematics and Physics, Hulunbuir University, Hulun Buir 021008, Inner Mongolia, China
In 1952, Turing [1] proposed a concept of "diffusion-driven instability", which means that if a constant equilibrium solution is stable in ODEs, it might become unstable when diffusions are introduced into the system. This kind of instability is really induced by diffusions. Nowadays, this instability is referred to as "homogeneity-breaking instability". It is known that if a constant equilibrium solution undergoes homogeneity-breaking instability, the system might have new non-constant steady state solutions.
In the past, most of the works focused on investigating the homogeneity-breaking instability of the constant equilibrium solution of the reaction-diffusion equations. However, few attention focused on studying the homogeneity-breaking instability of the periodic solutions except Refs.[2-5].
In this study, the diffusive Gierer-Meinhardt model is as follows:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} U}{\mathrm{~d} s}=D_{11} \Delta U+D_{12} \Delta V+ \\ \ \ \rho_U \frac{U^2 V}{1+K^2 U^2}-\mu_U U, x \in \Omega, s>0 \\ \frac{\mathrm{d} V}{\mathrm{~d} s}=D_{21} \Delta U+D_{22} \Delta V- \\ \ \ \rho_V \frac{U^2 V}{1+K^2 U^2}-\sigma_V, x \in \Omega, s>0 \\ \partial_\nu U=\partial_\nu V=0, x \in \Omega, s>0 \end{array}\right. $ | (1) |
where Ω ∈ Rn(n≥1) is a bounded open domain, with smooth boundary ∂Ω. Here U = U(x, s) and V = V(x, s) stand for the concentrations of the activator and inhibitor respectively at time s > 0 and a spatial position x ∈ Ω; D11, D22 > 0 are the diffusion coefficients of the activator and inhibitor, respectively; D12, D21 > 0 are the cross-diffusions coefficients; the parameters ρU, ρV, μU, σV and K are the positive real numbers.
Introducing new variables
| $ \begin{gathered} u=K U, v=\frac{\mu_U V}{\sigma_V}, u_0=k U_0 \\ v_0=\frac{\mu_U V_0}{\sigma_V}, t=\mu_U s, a=\frac{\mu_U \sigma_V}{K \mu_U^2}\\ b=\frac{\rho_V}{K^2 \mu_U}, d_{i j}=\frac{D_{i j}}{\mu_U} \end{gathered} $ |
We obtain
| $ \left\{\begin{array}{l} \frac{\partial u}{\partial t}=d_{11} u_{x x}+d_{12} v_{x x}+\frac{a u^2 v}{1+u^2}-u, \\ \quad(x, t) \in(0, \tau {\rm{ \mathsf{ π}}}) \times(0, \infty) \\ \frac{\partial v}{\partial t}=d_{21} u_{x x}+d_{22} v_{x x}-\frac{b u^2 v}{1+u^2}+1, \\ \quad(x, t) \in(0, \tau {\rm{ \mathsf{ π}}}) \times(0, \infty) \\ \partial_\nu u=\partial_\nu v=0, x \in \Omega, x=0, \tau {\rm{ \mathsf{ π}}}, t>0 \\ u(x, 0)=u_0(x) \geqslant 0, v(x, 0)=v_0(x) \geqslant 0, \\ \quad x \in(0, \tau {\rm{ \mathsf{ π}}}) \end{array}\right. $ | (2) |
The dynamics of system (2) when only diffusions (without cross diffusions) is present were considered by Wan et al. [6], who performed detailed Hopf bifurcation analysis on this reaction diffusion system (2). They not only proved the existence of Hopf bifurcations, but also derived the conditions to identify the characteristics of the bifurcating periodic solutions. However, homogeneity-breaking instability of the periodic solutions remains unsolved.
In Ref.[5], Yi used the perturbation method proposed by Maginu[2] to derive a sufficient condition for the periodic solution to undergo Turing instability diffusion rate in a general reaction diffusion equation with cross diffusion. The purpose of the current paper is to use the general results of Ref.[5] to consider the homogeneity-breaking instability of the bifurcating periodic with the reaction-diffusion Gierer-Meinhardt model. It is found that homogeneity-breaking instability of the Hopf bifurcating periodic solutions occurs under suitable conditions on diffusions and cross-diffusions.
1 Stability and Hopf Bifurcation Analysis of Kinetic ODEsThe ODEs of system (2) are as follows:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} u}{\mathrm{~d} t}=-u+\frac{a u^2 v}{1+u^2} \\ \frac{\mathrm{d} v}{\mathrm{~d} t}=1-\frac{b u^2 v}{1+u^2} \end{array}\right. $ | (3) |
Clearly, system (2) has a unique positive steady state solution (κ, vκ)∶=(κ, (κ2+1)/aκ), where κ∶=a/b. We use κ as the bifurcation parameter by fixing a > 0.
The linearized operator of system (2) evaluated at (λ, vλ) is given by:
| $ \boldsymbol{J}(\boldsymbol{\kappa}):=\left(\begin{array}{ll} a_*(\boldsymbol{\kappa}) & b_*(\boldsymbol{\kappa}) \\ c_*(\boldsymbol{\kappa}) & d_*(\boldsymbol{\kappa}) \end{array}\right) $ | (4) |
where
| $ \begin{gathered} a_*(\kappa)=\frac{1-\kappa^2}{1+\kappa^2}, b_*(\kappa)=\frac{a \kappa^2}{1+\kappa^2} \\ c_*(\kappa)=-\frac{2}{\kappa\left(1+\kappa^2\right)}, d_*(\kappa)=-\frac{a \kappa}{1+\kappa^2} \end{gathered} $ |
The characteristic equation of J(κ) is μ2-μT(κ)+ D(κ) = 0, where
| $ T(\kappa)=\frac{1-a \kappa-\kappa^2}{\kappa^2+1}, D(\kappa)=\frac{a \kappa}{\kappa^2+1} $ | (5) |
We would like to mention that for the reaction-diffusion Gierer-Meinhardt model (2) without cross-diffusion, Wan et al. [6] derived precise conditions on system parameters to study the existence and properties of the Hopf bifurcating periodic solutions.
In this section, we use the similar methods to study the existence and stability of the Hopf bifurcating periodic solutions for the ODEs System (3).
The results are as follows.
Theorem 1: Suppose that κ0 is the unique positive root of 1-aκ-κ2 = 0. Then, the following conclusions hold true:
1) (κ, vκ) is locally asymptotically stable in System (3) if κ ∈ (0, κ0), while unstable if κ ∈ (κ0, ∞);
2) When κ = κ0, the Hopf bifurcation of System (3) occurs around (κ, vκ). The bifurcating periodic solution, denoted by (u*(t), v*(t)), is locally orbitally asymptotically stable if a > 2/
Proof
1) For κ ∈ (0, κ0), we have T(κ) > 0, D(κ) > 0, which means the instability, and for κ ∈ (κ0, ∞), we have T(κ) < 0, D(κ) > 0. which induces the local stability of (κ, vκ).
2) At κ = κ0,
| $ \alpha(\kappa)=\frac{1}{2} T(\kappa), \omega(\kappa)=\frac{1}{2} \sqrt{4 D(\kappa)-T^2(\kappa)} $ | (6) |
The direct calculation results show as follows:
| $ \alpha^{\prime}\left(\kappa_0\right)=-\frac{a+2 \kappa_0}{2\left(1+\kappa_0{ }^2\right)}<0 $ | (7) |
Then, from the Hopf Bifurcation Theorem [3], system (2) has a Hopf bifurcation at (κ0, vκ0).
In the following, we consider the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions, denoted by (u*(t), v*(t)).
We translate (κ, vκ) to origin and let
| $ \left\{\begin{array}{l} u^{\prime}=-u-\lambda+\frac{a(u+\lambda)^2(v+\lambda)}{1+(u+\lambda)^2} \\ v^{\prime}=1-\frac{b(u+\lambda)^2(v+\lambda)}{1+(u+\lambda)^2} \end{array}\right. $ | (8) |
Rewrite system (8) in the following form:
| $ \binom{u^{\prime}}{v^{\prime}}=\boldsymbol{J}(\boldsymbol{\kappa})\binom{u}{v}+\binom{F_1(u, v, \kappa)}{G_1(u, v, \kappa)} $ | (9) |
where J (κ) is defined in Eq.(4) and
| $ \begin{aligned} F_1(u, v, \kappa)= & \frac{1-3 \kappa^2}{\kappa(1+\kappa)^2} u^2-\frac{2 a \kappa}{(1+\kappa)^2} u v+ \\ & \frac{4\left(1-\kappa^2\right)}{\left(1+\kappa^2\right)^2} u^3+\frac{a\left(1-3 \kappa^2\right)^2}{\left(1+\kappa^2\right)^3} u^2 v+ \\ & \mathrm{O}\left(|u|^4, |u|^3|v|\right) \\ G_1(u, v, \kappa)= & \frac{1-3 \kappa^2}{\kappa^2\left(1+\kappa^2\right)^2} u^2-\frac{2 a}{\left(1+\kappa^2\right)^2} u v+ \\ & \frac{4\left(1-\kappa^2\right)}{\kappa\left(1+\kappa^2\right)^3} u^3-\frac{a\left(1-3 \kappa^2\right)}{\kappa\left(1+\kappa^2\right)^3} u^2 v+ \\ & \mathrm{O}\left(|u|^4, |u|^3|v|\right) \end{aligned} $ |
Define a real 2-by-2 matrix
| $ \boldsymbol{Y}(\boldsymbol{\kappa})=\left(\begin{array}{cc} 1 & 0 \\ \frac{\kappa^2-a \kappa-1}{2 a \kappa^2} & -\frac{\left(1+\kappa^2\right) \omega}{a \kappa^2} \end{array}\right) $ |
By using the linear transformation
| $ \binom{u}{v}=\boldsymbol{Y}(\boldsymbol{\kappa})\binom{x}{y} $ |
We can simplify Eq.(9) into the following equations
| $ \binom{x^{\prime}}{y^{\prime}}=\left(\begin{array}{cc} \alpha(\boldsymbol{\kappa}) & -\omega(\boldsymbol{\kappa}) \\ \omega(\boldsymbol{\kappa}) & \alpha(\boldsymbol{\kappa}) \end{array}\right)\binom{x}{y}+\binom{F(x, y, \boldsymbol{\kappa})}{G(x, y, \kappa)} $ | (10) |
where α(κ) and ω(κ) are defined in Eq.(6), and
| $ \begin{aligned} F(x, y, \kappa):= & F_1\left(x, \frac{\kappa^2-a \kappa-1}{2 a \kappa^2} x-\right. \\ & \left.\frac{\left(1-\kappa^2\right) \omega}{a \kappa^2} y, \kappa\right) \\ G(x, y, \kappa):= & \frac{\kappa^2-a \kappa-1}{2 a \kappa^2} F(x, y, \kappa)-\frac{a \kappa^2}{\left(1+\kappa^2\right) \omega} \cdot\\ G_1(x, &\frac{\kappa^2-a \kappa-1}{2 a \kappa^2} x-\frac{\left(1-\kappa^2\right) \omega}{a \kappa^2} y, \kappa) \end{aligned} $ |
Taylor expanding F(x, y, κ) at (x, y)=(0, 0), we have
| $ \begin{aligned} F(x, y, \kappa) & =a_{20} x^2+a_{11} x y+a_{21} x^2 y+a_{30} x^3+ \\ & \mathrm{O}\left(|u|^4, |u|^3|v|\right) \end{aligned} $ | (11) |
where
| $ \begin{gathered} a_{\left.\right|_0}:=-\frac{a+2 \kappa}{\left(1+\kappa^2\right)^2}, a_{11}:=-\frac{2 \omega}{\kappa+\kappa^3} \\ a_{21}:=\frac{\omega\left(-1+3 \kappa^2\right)}{\kappa^2\left(1+\kappa^2\right)^2} \\ a_{30}:=\frac{-1-4 \kappa^2+5 \kappa^4+a \kappa\left(-1+3 \kappa^2\right)}{2 \kappa^2\left(1+\kappa^2\right)^3} \end{gathered} $ |
Similarly, Taylor expanding G(x, y, κ) at (x, y)=(0, 0), we have
| $ \begin{aligned} G(x, y, \kappa) & =b_{20} x^2+b_{11} x y+b_{21} x^2 y+ \\ b_{30} x^3 & +\mathrm{O}\left(|u|^4, |u|^3|v|\right) \end{aligned} $ | (12) |
where
| $ \begin{gathered} b_{20}:=-\frac{(a+2 \kappa)\left(-1+a \kappa+\kappa^2\right)}{2 \omega\left(1+\kappa^2\right)^3} \\ b_{11}:=-\frac{-1+a \kappa+\kappa^2}{\kappa\left(1+\kappa^2\right)^2} \\ b_{21}:=\frac{\left(-1+a \kappa+\kappa^2\right)\left(-1+3 \kappa^2\right)}{2 \kappa^2\left(1+\kappa^2\right)^3} \\ b_{30}:=\frac{\left(-1-4 \kappa^2+5 \kappa^4+a \kappa\left(-1+3 \kappa^2\right)\right)\left(-1+a \kappa+\kappa^2\right)}{4 \omega \kappa^2\left(1+\kappa^2\right)^4} \end{gathered} $ |
Following Refs.[5, 7-8], we define
| $ \begin{aligned} c_*\left(\kappa_0\right):= & \frac{i}{2 \omega\left(\kappa_0\right)}\left(h_{20} g_{11}-2\left|h_{11}\right|^2-\right. \\ & \left.\frac{1}{3}\left|h_{02}\right|^2\right)+\frac{h_{21}}{2} \end{aligned} $ | (13) |
where
| $ \begin{gathered} h_{11}:=\frac{1}{4}\left(F_{x x}+F_{y y}+i\left(G_{x x}+G_{y y}\right)\right) \\ h_{02}:=\frac{1}{4}\left(F_{x x}-F_{y y}-2 G_{x y}+i\left(G_{x x}-G_{y y}+2 F_{x y}\right)\right) \\ h_{20}:=\frac{1}{4}\left(F_{x x}-F_{y y}+2 G_{x y}+i\left(G_{x x}-G_{y y}-2 F_{x y}\right)\right) \\ h_{21}:=\frac{1}{8}\left(F_{x x x}+F_{x y y}+G_{x x y}+G_{y y y}+\right. \\ \left.i\left(G_{x x x}+G_{x y y}-F_{x x y}-F_{y y y}\right)\right) \end{gathered} $ | (14) |
where all the quantities are to be evaluated at (0, 0, κ0). Then, we have
| $\begin{aligned} &\operatorname{Re}\left(c_*\left(\kappa_0\right)\right)=\frac{1}{16}\left(F_{x x x}+F_{x y y}+G_{x x y}+G_{y y}\right)+\\ & \frac{1}{16 \omega\left(\kappa_0\right)} \cdot\left(F_{x y}\left(F_{x x}+F_{y y}\right)-G_{x y}\left(G_{x x}+G_{y y}\right)-\right. \\ & \left.F_{x x} G_{x x}+F_{y y} G_{y y}\right) \end{aligned} $ |
In the formula, F and G are solved for the partial derivatives at point (0, 0, κ0), and the following results are obtained.
Then, from Eqs.(11) and (12), we get
| $ \begin{aligned} & \operatorname{Re}\left(c_*\left(\kappa_0\right)\right)=\frac{3}{8} a_{30}+\frac{1}{8 \omega\left(\kappa_0\right)} a_{11} a_{30}= \\ & \frac{2 \kappa_0-a}{8 \kappa_0\left(1+\kappa_0{ }^2\right)^2} \end{aligned} $ | (15) |
Then, by Refs.[5, 7-8], if Re(c*(κ0)) < 0, then the Hopf bifurcating periodic solution is stable, while if Re(c*(κ0)) > 0, then the Hopf bifurcating periodic solution is unstable. One can check that if a > 2/
Remark 1 From Eqs.(11) and (12), we also have
| $ \begin{aligned} \operatorname{Im}\left(c_*\right. & \left.\left(\kappa_0\right)\right)=\frac{1}{16}\left(G_{x x x}+G_{x y y}-F_{x x y}-F_{y y}\right)- \\ & \frac{1}{16 \omega\left(\kappa_0\right)}\left(\left(F_{x x}+F_{y y}\right)^2+\left(G_{x x}+G_{y y}\right)^2\right)+ \\ & \frac{1}{32 \omega\left(\kappa_0\right)}\left(\left(F_{x x}+F_{y y}\right)\left(F_{x x}-F_{y y}+2 G_{x y}\right)-\right. \\ & \left.\left(G_{x x}+G_{y y}\right)\left(G_{x x}-G_{y y}-2 F_{x y}\right)\right)- \\ & \frac{1}{96 \omega\left(\kappa_0\right)}\left(\left(F_{x x}-F_{y y}-2 G_{x y}\right)^2+\right. \\ & \left.\left(G_{x x}-G_{y y}-2 F_{x y}\right)^2\right)= \\ & -\frac{1}{8} a_{21}-\frac{1}{6 \omega\left(\kappa_0\right)} a_{20}^2-\frac{1}{24 \omega\left(\kappa_0\right)} a_{11}^2= \\ & -\frac{a\left(1+9 \kappa_0^2\right)\left(1+\kappa_0^2\right)+4 \kappa_0\left(a+2 \kappa_0\right)^2}{24 \omega\left(\kappa_0\right) \kappa_0\left(1+\kappa_0^2\right)^4} \end{aligned} $ | (16) |
Remark 2 A periodic solution (u*(t), v*(t))=(u*(t+P), v*(t+P)) is said to be orbitally stable if the set M = {(u*(t), v*(t)), 0 ≤ t ≤ P} is stable. Similarly, orbital asymptotic stability, orbital instability all refer to the corresponding stability property of the set M.
2 Homogeneity-Breaking Instability of Periodic Solutions in Spatial SystemsIn this section, the homogeneity-breaking instability of the Hopf bifurcating spatially homogeneous periodic solution (u*(t), v*(t)) obtained in Theorem 1 will be discussed.
| $ \left\{\begin{array}{l} \frac{\partial u}{\partial t}=d_{11} u_{x x}+d_{12} v_{x x}+\frac{a u^2 v}{1+u^2}-u, \\ \quad(x, t) \in(0, \tau {\rm{ \mathsf{ π}}}) \times(0, \infty) \\ \frac{\partial v}{\partial t}=d_{21} u_{x x}+d_{22} v_{x x}-\frac{b u^2 v}{1+u^2}+1, \\ \quad(x, t) \in(0, \tau {\rm{ \mathsf{ π}}}) \times(0, \infty) \\ \partial_\nu u=\partial_\nu v=0, x \in \Omega, x=0, \tau {\rm{ \mathsf{ π}}}, t>0 \\ u(x, 0)=u_0(x) \geqslant 0, v(x, 0)=v_0(x) \geqslant 0, \\ \quad x \in(0, \tau {\rm{ \mathsf{ π}}}) \end{array}\right. $ | (17) |
where τ > 0.
Following Refs.[2, 5], we shall reduce the problem of homogeneity-breaking instability of the periodic solution (u*(t), v*(t)) to the problem of the following perturbed planar system as follows:
| $ \left(\boldsymbol{I}+\varepsilon\left(\begin{array}{ll} d_{11} & d_{12} \\ d_{21} & d_{22} \end{array}\right)\right)\binom{u^{\prime}}{v^{\prime}}=\binom{-u+\frac{a u^2 v}{1+u^2}}{1-\frac{b u^2 v}{1+u^2}} $ | (18) |
where |ε| is sufficiently small. According to the Theorem 3.3 of Ref.[5] (see also Ref.[9] for a more general version), we have the following theorem.
Lemma 1[5] It assumes that the stable Hopf bifurcating periodic solution (u*(t), v*(t))with the minimum period P of the ODE system (3) exists as proclaimed in Theorem 1. Then, if the |ε| is sufficiently small, a stable periodic solution which is denoted by (u*(t, ε), v*(t, ε)) with the minimum period P(ε)of the perturbed system (18) will also exists, a C1 function of the parameter ε, such that as ε→0, P(ε)→P and (u*(t, ε), v*(t, ε))→(u*(t), v*(t)).
By Theorem 3.5 of Ref.[5] (or Ref.[2] for the unbounded domain case), if the perturbed system (18) has a periodic solution (u*(t, ε), v*(t, ε)), with the minimum period P(ε), then homogeneity-breaking instability of the periodic solution (u*(t), v*(t)) with respect to the reaction-diffusion system (17) occurs if P′(0) < 0 and ℓ is chosen to be sufficiently large.
Moreover, we use the diffusion rates d11, d12, d21 and d22 to express the condition P′(0) < 0 based on that the stable periodic solution of the ODE system (3) is indeed the Hopf bifurcating periodic solution.
Lemma 2[5] It supposes that κ is steadily approaching and sufficiently close to κ0 thus (u*(t), v*(t)) is a stable periodic solution of system (3) bifurcating from (κ, vκ)T at κ = κ0 as stated in Theorem 1. In particular
| $\begin{array}{l} \frac{\operatorname{Im}\left(c_*\left(\kappa_0\right)\right)}{\operatorname{Re}\left(c_*\left(\kappa_0\right)\right)}\left(d_{11}\left(-\frac{a \kappa_0}{\kappa_0{ }^2+1}\right)+d_{22} \frac{1-\kappa_0{ }^2}{\kappa_0{ }^2+1}-\right. \\ \ \ \ \ \left.d_{12} \frac{a \kappa_0}{\kappa_0{ }^2+1}-d_{21}\left(-\frac{2}{\kappa_0\left(\kappa_0{ }^2+1\right)}\right)\right)+ \\ \ \ \ \ \sqrt{D\left(\kappa_0\right)}\left(d_1+d_2\right)<0 \end{array} $ | (19) |
where Re(c*(κ0)) and Im(c*(κ0)) are defined in Eqs.(15) and (16) respectively. Then, (u*(t), v*(t))T is unstable with respect to System (17) if a is large enough.
Note that
| $ \begin{aligned} & \frac{\operatorname{Im}\left(c_*\left(\kappa_0\right)\right)}{\operatorname{Re}\left(c_*\left(\kappa_0\right)\right)}= \\ & \quad-\frac{a\left(1+9 \kappa_0^2\right)\left(1+\kappa_0^2\right)+4 \kappa_0\left(a+2 \kappa_0\right)^2}{3 \omega\left(\kappa_0\right)\left(1+\kappa_0^2\right)^2\left(2 \kappa_0-a\right)} \end{aligned} $ | (20) |
Then, P′(0) < 0 is equivalent to
| $ \begin{gathered} 2\left(1+9 \kappa_0^2\right) d_{11}+2\left(9 \kappa_0^4-3 \kappa_0^2-4\right) d_{22}+(5+ \\ \left.12 \kappa_0^2-9 \kappa_0^4\right)\left(-\frac{2}{a \kappa_0^2} d_{12}+\kappa_0 d_{21}\right)<0 \end{gathered} $ | (21) |
The homogeneity-breaking instability of the periodic solution (u*(t), v*(t))can be summarized as follows.
Theorem 2 Suppose that (u*(t), v*(t)) is the stable periodic solution of system (3) bifurcating from (κ0, vκ0) as stated in Theorem 1. Then (u*(t), v*(t))undergoes homogeneity-breaking instability in system (17), if τ is sufficiently large and
| $ \begin{gathered} 2\left(1+9 \kappa_0^2\right) d_{11}+2\left(9 \kappa_0^4-3 \kappa_0^2-4\right) d_{22}+(5+ \\ \left.12 \kappa_0^2-9 \kappa_0^4\right)\left(-\frac{2}{a \kappa_0^2} d_{12}+\kappa_0 d_{21}\right)<0 \end{gathered} $ |
where Re(c*(κ0)) and Im(c*(κ0)) are in the forms of Eqs.(15) and (16) respectively.
3 Numerical SimulationsIn order to strengthen our analytical analysis, we shall use numerical simulations in this subsection. Assume a≈2.25, we have κ0=0.3802. which satisfies the condition of Theorem 1.
Case 1 (Homogeneity-breaking instability fails): a≈2.25 and κ0=0.4, d11 = d12=1>0 = d21 = d22. No homogeneity-breaking instability of (u*(t), v*(t)) could be found. (u*(t), v*(t)) is also stable in PDEs. (See Fig. 1)

|
Fig.1 U-component and V-component (Case 1) |
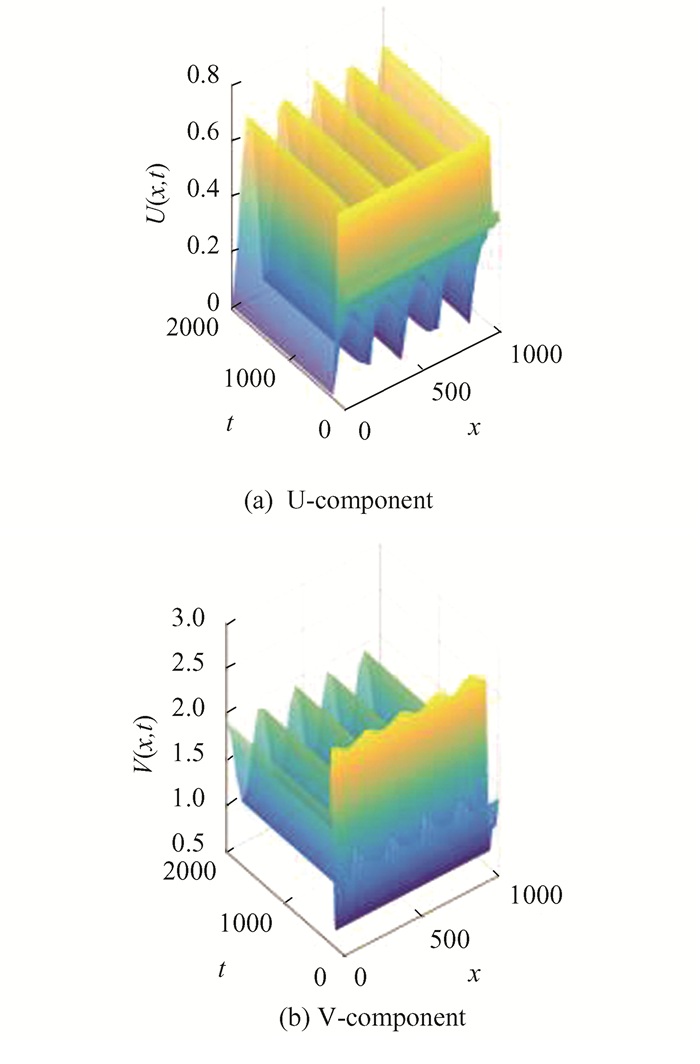
Case 2 (Diffusion induced homogeneity-breaking instability): a≈2.25 and κ0=0.3665, d12 = d21=0, d11=200, d22=2300. Diffusions really induced homogeneity-breaking instability. (See Fig. 2)
|
Fig.2 U-component and V-component (Case 2) |
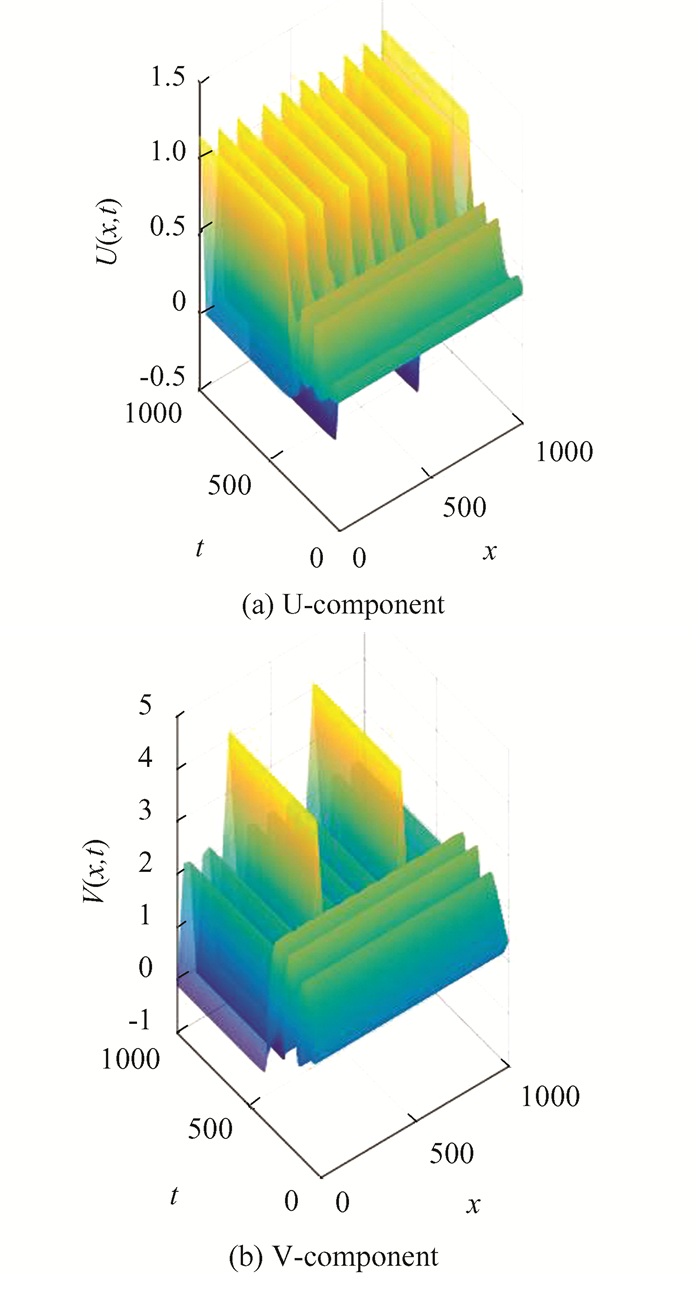
Case 3 (Diffusions and cross-diffusion jointly induced homogeneity-breaking instability): a≈2.25 and κ0=0.3665, d11=30, d22=621, d12=19, d21=926. Diffusions and cross-diffusions really induce homogeneity-breaking instability. (See Fig. 3)
|
Fig.3 U-component and V-component (Case 3) |
4 Conclusions
In this paper, we studied the stability of constant equilibrium solutions and spatially homogeneous periodic solutions, as well as homogeneity-breaking instability, for the cross diffusion Gierer-Meindardt model. The research results indicate that when the diffusion coefficient difference is large, the spatial homogeneous periodic solution of the system experiences Turing instability.
| [1] |
Turing A M. The chemical basis of morphogenesis. Phil. Trans. Royal Soc. London, 1952, 237: 37-72. DOI:10.1016/S0092-8240(05)80008-4 (  0) 0) |
| [2] |
Maginu K. Stability of spatially homogeneous periodic solutions of reaction-diffusion equations. J. Differential Equations, 1979, 31(1): 130-138. DOI:10.1016/0022-0396(79)90156-6 (  0) 0) |
| [3] |
Ruan S. Diffusion-driven instability in the Gierer-Meinhardt model of morphogenesis. Nat. Resour. Model., 1998, 11(2): 131-142. DOI:10.1111/j.1939-7445.1998.tb00304.x (  0) 0) |
| [4] |
Wang M, Yi F. On the dynamics of the diffusive Field-Noyes model for the Belousov-Zhabotinskii reaction. J. Differential Equations, 2022, 318: 443-479. DOI:10.1016/j.jde.2022.02.031 (  0) 0) |
| [5] |
Yi F. Homogeneity-breaking instability of the periodic solutions in general cross-diffusion PDEs and the patch model with diffusion-like coupling. J. Differential Equations, 2021, 281: 397-410. (  0) 0) |
| [6] |
Wan A, Yi F, Zheng L. Hopf bifurcation analysis and oscillatory patterns of a diffusive Gierer-Meinhardt model. Acta Math. Sci., 2015, 35A(2): 381-394. (  0) 0) |
| [7] |
Hassard D D, Kazarinoff N D, Wan Y-H. Theory and Application of Hopf Bifurcation. Cambridge: Cambridge University Press, 1981.
(  0) 0) |
| [8] |
Marsden J E, McCracken M. The Hopf Bifurcation and its Applications. New York: Springer, 1976. DOI:10.1007/978-1-4612-6374-6
(  0) 0) |
| [9] |
Grant C P. Theory of Ordinary Differential Equations. Provo: Brigham Young University, 2008.
(  0) 0) |
 2024, Vol. 31
2024, Vol. 31


