Investigation connected to the turbine engine aims to lower cost as well as weight. The effortless and the best reasonable accomplishment of this objective is to lower the number of blades. With a decrease in blade count, the pitch spacing increases, and consequently, an increase in loading per blade occurs. However, high-lift vanes have substantial losses from the junction flow, owing to the significant influence of pressure gradients that increase the boundary layer detachment, which fortifies the secondary flow field vortical features. The endwall secondary flows are evaluated to constitute 33%-50% of the loss by high-lift turbine blade rows[1]. Contouring the blade, as well as the endwall, comprise passive flow control[2]; the plasma actuators and the steady or unsteady blowing comprise active flow control[3]. The enhanced effects of passive heat transfer are by incorporating a working media with high heat capacity to improve system efficiency and reduce the cost of operation[4].
An understanding of the natural instabilities of the passage flow structures is key to implementing these unsteady active methods. As reported previously, a gradual pressure recovery over the suction surface can be brought out by loading a profile on the front side capable of a high lift[5]. The generation of losses by the secondary flows in the endwall region needs better understanding, even with an excellent improvement at the midspan with the blades having a high lift. Awareness of the hydrodynamics of the endwall can proceed to the development of superior numerical methods of design and competencies to ward off the penalties concerning the endwall domain. The secondary flows are 3D in nature and complex, formed by the turbine endwalls with the vanes and the various features of the flow govern the film cooling and heat transfer[6].
A thermographic method was used to measure the suction surface endwall distribution of a vane cascade at different levels of Reynolds number (Re, 5×105 to 2×106) and turbulence intensities (0.7% to 17.4%) to depict complete visualizations of their combined effects[7]. The turbulence intensity used for the heat transfer in the transonic turbine stage was 4% and 7.8%[8]. The turbulence intensity set for the mean heat transfer of an airfoil was 8%[9]. The Reynolds number for the aerothermal performance of the turbine endwall was 4.2×105 [10]. The Reynolds number for the effects of axisymmetric convergent contouring of the endwall was 1.7×106[11].
Though predictions using SST (Shear Stress Transport)-TRANS models were a high replica of experimental values concerning secondary flow regions and heat transfer, the suction side trailing edge turbulence transition could not be evidenced. High-fidelity secondary flow simulations of the vane cascade passage are rare due to the high cost and lack of experimental data[12-14]. The coefficients of pressure and pitch average losses concerning secondary flows with inflow turbulence of 5% in a turbine cascade using LES (Large Eddy Simulation) were estimated and validated[14]. A shape function and cooling hole positions were optimized from an efficient turbine endwall cooling by multi-fidelity simulations[15]. The influence of different flow angles and turbulence on endwall heat transfer was elucidated using RANS and k-ω, BSL (Baseline model), and SST models, numerically and experimentally[16]. The size and strength of the vortex and hence the endwall heat transfer were over-predicted by the RANS models and hence periodic corrections and improvements are inevitable. The coefficients of mass and heat transfer can be equated as Sh ≈ Nu either by observation of Sh ≈ Pr or by fitting correlations[6, 9]. Where Sh represents the Sherwood number, Nu represents the Nusselt number, and Pr is the Prandtl number. Experimental data confirmed similar values of transport diffusivities[17], making Prt ≈ Sct. Prt is the turbulent Prandtl number, and Sct is the turbulent Schmidt number.
Endwall heat transfer and secondary flows in a turbine cascade having a substantial leading edge are performed by LES, with the geometry similar to the experimental data[7], at Re 5×105 for inlet flow turbulence intensity (Tu) cases of low (Tu ≈ 0%) and high (Tu ≈ 8%) turbulence. Turbulence effects on mid-span boundary conditions and heat transfer are highlighted[18]. The boundary layer is found to be laminar even at 12.4% inflow turbulence[19]. The mass transfer coefficients on the turbine endwall revealed that, as the diameter of a rod placed facing the vane increased, a turbulent boundary layer developed[20]. At high inflow turbulence intensities, the suction side laminar boundary layer becomes turbulent[21]. The second and first-order statistics concerning the turbulence transition via inner mode were reported[19]. The turbulence changes the thermal exchange by narrowing the entrance layer of the boundary concerning the turbine endwall and the topmost augmentation is evident at the reduced Re of 1.0×105 and elevated Re yields a reduced enhancement[22]. The prediction accuracies are compared using the distribution of St on top of the vane suction surface with its constituent experimental values in Ref. [7].
A linear vane cascade is simulated by Ansys Fluent[23] with RANS, combining SST eddy viscosity[24] with Reθ-γ[25] for the hydrodynamics and endwall heat transfer. The Reθ-γ model can utilize only the local information and correlations of experimental data that causes the transition. Passage 3D secondary flows and high aspect ratio (H ≫ C), blades with large blade midspan 2D region having minimal secondary flows at an exit Re 5×105 and inflow turbulence 0.2% and 4% are performed. Where H is cascade height, C is blade chord. This study is aimed to brighten the knowledge on gas turbine cooling at regions on the endwall that have the greatest outstanding influence on the aerodynamic or endwall thermal exchange accomplishments. The novelty of the present study is the establishment of the impact of a three-dimensional vortical structure greatly on turbine endwall heat transfer to reduce the weight and cost of a turbine engine.
1 Materials and MethodsComputations consist of one vane (blade inlet angle is 35°) alone with the periodicity along the pitch (separates boundaries) with an aspect ratio of 2.5 and P = 0.75 L. P is cascade pitch, pressure, and L is true chord length. The leading-edge origin is with positive suction side values. The local coordinate d, the normal axis with the vane surface, has a vane surface origin (d = 0). The z-axis is having an endwall origin (z = 0). Turbulence length is imposed in every direction (0.04 L). The inlet boundary (x = -0.5 L) with the endwalls at both ends of the vane is having 0.5 L total span. With 0.04% inflow turbulence, vane midspan is a symmetry plane, but a full vane is considered for the 8% inflow turbulence. A thin Blasius boundary layer is imposed at the inlet, covering only 3% of the vane span with Rex = 1.6×105 and δ99 = 0.015 L, normal to the endwall for the low inflow turbulence as reported[26]. Where δ99 boundary layer thickness(m). An inlet turbulent boundary layer having Reθ=1400 is imposed for the high inflow turbulence as reported[27], using the Synthetic Eddy Method[28] and the reported statistics[29]. Reθ is the transition model.
The inlet turbulence depends on the flow conditions upstream of the inlet. Inlet turbulence is treated by changing Re and hydraulic diameter. The turbulent intensity is taken from a fully developed inlet profile, generated using a shorter domain with a periodic boundary condition. The typical ranges of turbulence intensity are chosen for different upstream flow conditions. Turbulence intensity is chosen as high (5% - 20%) for rotating parts with high flow speeds, medium (1% - 5%) for internal pipe flows with low flow speeds, low (0.05% - 1%) for external hydrodynamic flows with slow-flowing fluids, and treated almost equally to no turbulence (< 0.05%). But, for CFD problems, a medium intensity is most commonly specified, in particular for internal flows. An ad-hoc turbulence intensity of 4%-20% (medium to high) as in most industrial applications is also considered. Hence, to have a better understanding of turbulence intensity, this investigation is treated in the range of 0.04, 0.2, 4, and 8 to represent one turbulence intensity each from all the above four categories.
LES is performed with a laminar Pr of 0.7 using Ansys Fluent. The trailing edge is distant 0.4 L from the outlet, consistent Neumann boundary conditions to the velocity, temperature, and pressure fields, and No-slip boundary conditions to the vane and endwalls are imposed. Uniform heat flux to the vane, endwall heating condition of the leading edge at 0.15 L upstream, and an adiabatic condition at its upstream are provided. After at least 6 flowthrough times of initialization, time-averaged all the quantities for 10 and 30 flow-through times Lx/uin. Lx represents axial chord length (m), uin is inlet velocity (m/s). Fluid properties are imposed as constants, as it is a low-speed simulation with de-coupling of the energy and momentum equations and independently solved.
1.1 Computational Domain and MeshThe inlet is located 0.75Cax blade upstream leading edge and the outlet is located at Cax downstream trailing edge (Fig. 1). Cax represents the blade axial chord. The domain reaches out spanwise for half of its elongation concerning 1.8Cax. Software (Fluent) is used to generate a mesh with the endwall surface mesh separation line upstream is structured and other bounding surfaces are triangular unstructured (Fig. 2). Bulk is composed of tetrahedral with limited pyramidal as a transition to hexahedral elements that maintain orthogonal and easy implementation. No prism elements were used and are refined in high curvatures.

|
Fig.1 Schematic diagram of the linear vane cascade |

|
Fig.2 Mesh details in the blade endwall region |
The whole domain for contoured endwall using Spalart-Allmaras turbulence model with 743310, 800082, 839262, 984142, and 1043762 mesh elements when subjected to grid independence study revealed that the grid number 800082 satisfies the numerical simulation requirements[30]. A grid-independence test is done in which the CFD domains with 0.2, 0.4, 0.8, 1.2, and 1.6 million grid points were checked and the meshing approach for the 1.2 million grid points is suitable to the CFD solutions for the contoured endwall using SST turbulence model[31]. After grid independence verification, the number of grid cells for the contoured endwall is set to 725000 using the SST turbulence model coupled with the Reθ-γ transition model[32]. At first, the range of meshes selected was wide with 5×105, 1×106, and 5×106 meshes; thus, mesh size 1×106 was identified to have only a slight variation from the 5×106 mesh size. Grids with 1, 1.5, and 2 million nodes were used for the grid independence study. No significant difference is noticed for the two latter cases. A grid spacing of 6.5 microns fine in the viscous sub-layer near the wall is used to meet the y+<1 requirement for the transition modeling. Where y+ represents the dimensionless wall distance.
1.2 Initial and Boundary ConditionsA nested grid is used for the vane surface proximity grid refining and on the pressure surface as well as the boundary layer of streamwise trajectory. The Stanton number, St is well predicted over the suction surface including the transition and the maximum d+ = 0.1 over the pressure surface. d+ is dimensionless wall-normal distance from the surface. The experimental uncertainty is St±12%[12], whereas the RMS (Root Mean Square) error in the predictions is 9%. Convergence is checked with the RMS below 10-6 upon termination after 2400 iterations.
Fig. 3 compares the predicted time averaged St with the experimental values[21] over the vane midspan as s/L function at high inflow turbulence. s/L represents the surface distance from the leading edge concerning true chord length, and s is the surface distance from the leading edge(m). Current predictions are inside the communicated variability of the experimental values. The stagnation point is s/L=0 and the positive and negative surface distances are of the suction and pressure sides. The spanwise endwall and midspan locations are z/L=0 and 0.25.z/L is the span-wise distance concerning true chord length.
| $\text { St }=h /\left(\rho\left\|u_{\text {outflow }}\right\| C_p\right)$ | (1) |

|
Fig.3 Comparison of Stanton number distribution with the experimental values[21] |
where
| $h=q_w /\left(T_w-T_0\right)$ | (2) |
Cp is specific heat capacity (J/kg·K); ρ is fluid density; qw is surface heat flux; Tw is wall temperature; T0 is inflow temperature.
The exit velocity ||uoutflow|| is calculated as the average of the velocity magnitude at the outflow plane subtracting the endwall boundary layer and the exit-to-inlet velocity ratio is found as 4. The secondary flow hydrodynamics is captured well and with an accurate fit for the suction side heat transfer, and with valid secondary flow predictions; the characteristics of the present geometry can be estimated with more clarity.
1.3 Comparison of Mass and Heat TransferWhen Schmidt number Sc equals Prandtl number Pr, Sh retrieved in simulations equals Nu in the experiment. The flow is dependent only on Re and thus will be the same and used the mass transfer runs with an Sc of 2.28[33] for a geometry. The thermal conductivity of CuO-H2O nanofluid was altered to enhance the Pr to 2.28 for the high inflow turbulence case.
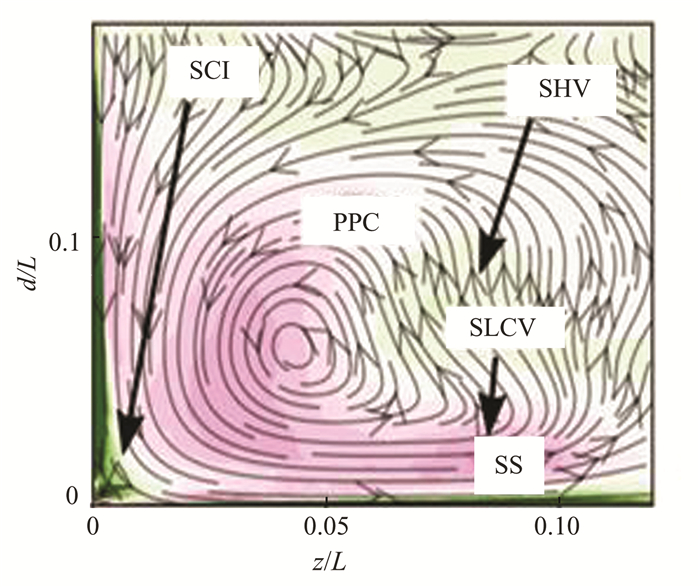
2 Results and Discussion 2.1 Passage CirculationThe development and progression of vane cascade passage secondary flow features are delineated at four different inflow turbulence intensities (Tu= 0.04, 0.2, 4, 8). Planes are circular corresponding to 0.02<s/L ≤ 0.22 and covering the full passage cross-section representing all the secondary flow formations. Planes are planar concerning s/L ≥ 0.24 and straight to the suction surface. The plotting of streamlines was done by subtracting z/L ≥0.25 from the in-plane velocity field, with the sampling plane local normal vector at the respective x and y[6]. Where x, y, and z represent axial, pitch-wise, and spanwise directions of cascade respectively.
2.1.1 Low turbulence inflowProgression of the time-averaged secondary flows with the plane flow direction with the marked pressure and suction surfaces for the low inflow turbulence are shown in Fig. 4. The contour shows the normal vorticity component with the shades of green rotating clockwise and the shades of red rotating anti-clockwise is also depicted. The core of the pressure side passage circulation is identified as the endwall adjacent and attached to it up to s/L ≈ 0.22 and relocates downstream towards the suction surface. The suction side passage circulation disappears as it fully wraps around the pressure side passage circulation around s/L ≈ 0.45. The suction side leading edge corner vortex strikes away the endwall location and is involved at s/L ≈ 0.4 in the passage vortex. At s/L ≈ 1.1 (close to the trailing edge), the pressure side cores of the passage circulation and suction side leading edge corner vortex are at equal wall distance and near the suction surface.

|
Fig.4 Evolution of the secondary flow time averaged contours with Tu≈0%, s/L≈1.2 |
The existence of the large leading edge turns the inlet boundary layer and a passage circulation pair is formed. The turning speed of the low momentum fluid of the endwall boundary layer is high compared to the high momentum fluid of the free stream. A secondary flow is seen formed near the end wall and this flow sweeps away the incoming flow from both sides of the vane (Fig. 5). The fluid from the end wall gets lifted at the stagnation point formed and thus, a pair of flow circulation rotating clockwise (suction side) and counter-clockwise (pressure side) is formed. The streamlines of velocity parallel to the endwall for the low free stream (Tu≈ 0) condition is shown in Fig. 5. It is evident that at a surface distance, s/L ≈ 0.02, where the planes are passage covering in full and circular, express all the features of the secondary flow with the stagnation point corresponds to d/L ≈ 0.45. d/L is the wall-normal distance concerning true chord length. The pressure side passage circulation moves towards the suction surface downstream and squeezes the suction side passage circulation, and combines to evolve a system of multi-vortex. The most dominant vortex system is the passage multi-vortex[16, 34]. The vane geometry consisting of a large leading edge might be the cause of the dominance of pressure side passage circulation over suction side passage circulation for this flow configuration.

|
Fig.5 Limiting velocity streamlines at the turbine endwall with Tu≈0, s/L≈0.02, z/L ≈ 0.0015 |
2.1.2 High turbulence inflow
The core of the pressure side passage circulation is outside the limits of the endwall unlike in the low inflow turbulence case and is carried forward to the suction surface soon after its entry in the passage. The core of the suction side passage circulation continues to be different till the trailing edge as shown with the pressure and suction surfaces in Fig. 6. The flow direction of the time-averaged secondary flow formation is along the planes. Normal vortices are highlighted in the contours with the green shades rotating clockwise and the red shades rotating anti-clockwise. The streamlines of velocity parallel to the endwall for Tu=8% condition is shown in Fig. 7. The location of the core of the pressure side passage circulation and suction side passage circulation is non-obvious, pending s/L=0.08, planar planes are normal to the suction surface, at this location. The stagnation point corresponds to d/L=0.45. The pressure side and suction side passage circulation cores are at a long way distance concerning the endwall. The high amount of fluid having low momentum in the latter case might be increasing the thickness of the endwall crossflow and pushing the cores away from the endwall. The main difference in interaction dynamics for the high turbulence inflow condition from the free stream inflow condition is that the core of the suction side passage circulation remains distinct till reaching the trailing edge. The pressure side passage circulation core and the suction surface never adjoin.
|
Fig.6 Evolution of the secondary flow time averaged contours with Tu≈8%, s/L≈1.2 |

|
Fig.7 Limiting streamlines at the turbine endwall with Tu≈8%, s/L≈0.02, z/L≈0.015 |
2.2 Endwall Heat Transfer
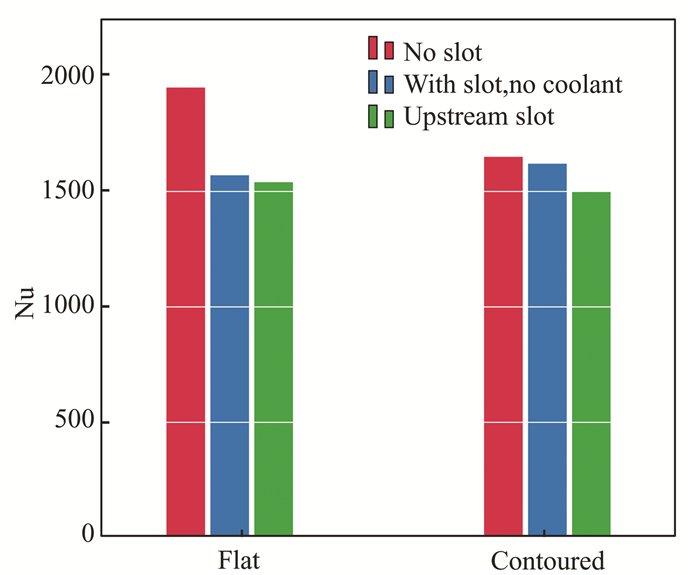
Thermal exchange in the absence of an upstream slot upon endwall contouring was performed[35]. In uncooled cases where slots exist, its outlet is not sealed and hence, the mainstream enters inside when the injection is absent. In uncooled cases, laterally averaged endwall Nu across the axis for contoured and flat shapes was shown in Fig. 8. Non-existence of leakage flow highlights the impact of appending the backward-facing purge slot upstream on endwall thermal exchange. The individual upstream purge slot impact without endwall contouring is also discernible in Fig. 8. The principal slot impact is diminishing endwall heat flux downstream across the passage and the impact on leading-edge thermal exchange is minimal. This might be due to the debilitating passage vortex development owing to the existence of slots and diminished by the impact of contouring.

|
Fig.8 Laterally averaged endwall Nu for different endwall shapes under upstream purge flow and without cooling |
The arriving layer of boundary deviates on the point of stagnation, upstream of the leading edge and develops a horseshoe vortex for a flat endwall. The horseshoe vortex with its pressure side leg migrates to the passage interior and develops in intensity upon interacting with the mainstream. The pressure differential of the cross-passage developed among the suction as well as the pressure sides of the nearby blades makes the passage vortex move to the suction side of the vane, merge with the horseshoe vortex suction side leg in the endwall region, and migrate away. The corner vortex sticks and extends to develop across the vane suction side till the trailing edge. The passage vortex develops then towards the trailing edge, sticking to the vane suction side.
The design of the contoured endwall makes the horseshoe vortex pressure side leg, redirected to the stream. The projected portion from the leading edge to the suction side concerning the contoured endwall prevents the passage vortex from transcending the passage even if an elevated pressure gradient exists. Hence, the passage vortex keeps debilitated than the flat endwall having a meager pressure differential at the cross-passage and is directed by the peak zone to force the merger location with the horseshoe vortex suction side leg still downstream than that in the flat endwall. The trajectory and vigor of the passage vortex are responsible for the hot gas entrainment to the endwall and are pivotal in endwall thermal exchange. Local Nu is under the impact of flow characteristics adjacent to the endwall and elevated Nu is evident with powerful vortices.
Laterally averaged endwall Nu across the axis, with the film-cooling having coolant to mainstream MFR of 1.5% for both endwall geometries is depicted in Fig. 8. Nu showed an outstanding association of secondary flow structures and coolant. The upstream slot leakage flow trajectory among the pressure side leg and the suction side horseshoe vortex of the nearby blades has gently vanished towards the mainstream. The intensification of the coolant vortex by slot induction elevates coolant momentum flux and led to enhanced HTC at which the laterally averaged Nu manifests a greater peak before the leading edge. Augmentation of the endwall thermal load owing to the merger of coolant is also evident for the contoured case but with a downstream migration than in the flat case. An elevated rate of coolant flow predominantly lowers the thermal load adjacent to the upstream and leading edge for the contoured case. The Nu disruption among the top and bottom windows at the zone of overlap differs by up to 16% (Fig. 8). This might be owing to the intrinsic complications of keeping similar operating conditions for the entire endwall. The capability of coolant flow as well as its loop of heating/cooling is forced to its operational limits, leading to the struggle of reiterating each situation separately, but this disruption is nearly absent for every uncooled case. The impact of this disruption on gross mean thermal exchange provisions does not change the significant interpretations inferred from the outcomes. The coolant distribution across the mainstream is not predominantly elevated due to possible coolant lift-off from the endwall.
The upstream purge flow has been matched without coolant (with a slot) and without slot cases in respect of area-averaged endwall Nu of flat and contoured endwalls (Fig. 9). The contoured geometries showed a 15.4%, 3.2%, and 2.7% reduction in endwall Nu than their respective flat geometries concerning no slot, with slot (no coolant) and upstream slot respectively. An outstanding lowering in endwall Nu (9% more than the contoured case and 23% more than the flat case) was attained owing to the sole existence of the upstream slot.
|
Fig.9 Area averaged endwall Nu for different endwall shapes and slot conditions |
The Nu disruption among the top and bottom windows at the zone of overlap differs by up to 16%. The contoured geometries showed a 15.4%, 3.2%, and 2.7% reduction in endwall Nu than their respective flat geometries concerning no slot, with slot (no coolant) and upstream slot respectively. An outstanding lowering in endwall Nu (9% more than the contoured case and 23% more than the flat case) was attained owing to the sole existence of the upstream slot.
The heat transfer distribution (Stanton number) over the endwall for the low free stream (Tu≈0) and high inflow turbulence (Tu≈ 8%) conditions are depicted (Figs. 10-15).
|
Fig.10 Turbine Endwall Stanton number distribution at Tu≈0 |

|
Fig.11 Sherwood number contour on endwall surface of the turbine at Tu≈0.2% |

|
Fig.12 Sherwood number line plots on the endwall surface of the turbine at Tu≈0.2% |

|
Fig.13 Turbine Endwall Stanton number distribution at Tu≈8% |

|
Fig.14 Sherwood number contour on endwall surface of the turbine at Tu≈4% |

|
Fig.15 Sherwood number lineplots on the endwall surface of the turbine at Tu≈4% |
2.2.1 Low inflow turbulence
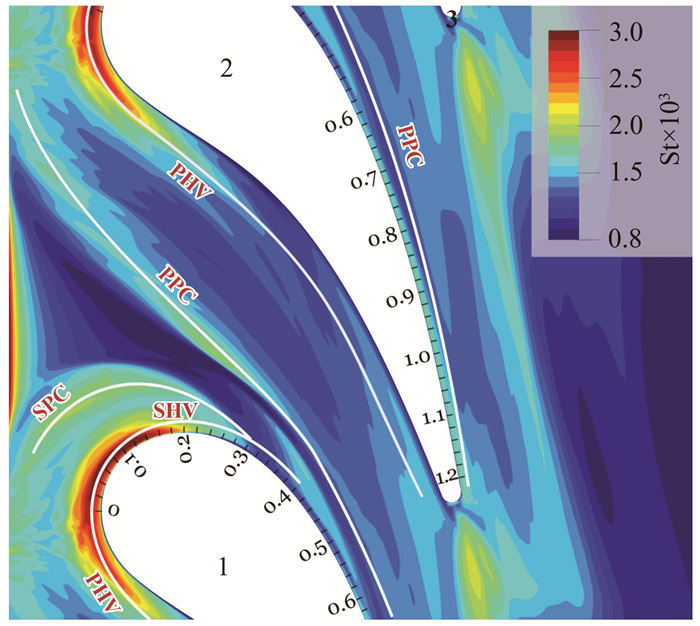
As the core of the pressure side and suction side passage circulation is near the endwall, Fig. 10 depicts the areas of high heat transfer present, lower to the core of these features. Minute markings of high St below the pressure side passage circulation core diminish starting from the endwall separation location. Starting from this separation location, the suction side passage circulation and the enclosed suction side horseshoe vortices leave the location of the endwall far off, and hence after do not increment the endwall heat transfer. A band of shallow coefficient of heat transfer containing surplus fluid produces a component of normal velocity to the endwall and creates a thickly layered boundary. The endwall surface Sh distributions are depicted in Figs. 11 and 12. The leading-edge mass transfer enhancement is fully evident using the SST-TRANS model and provided in Fig. 12. The horseshoe vortex of the pressure side is distinctly visible within its contour plot location (Fig. 11) and is visible as a peak that proceeds beyond the passage in the line plots (Fig. 12).
The corner vortex having a very restricted vigor generates a powerful fluid acceleration in the direction of cross-flow that makes a thinner boundary layer and a hike in the rates of mass transfer. This event is obvious in the turbine vane cascade simulations when performed using the models such as the Spalart-Allmaras, RNG (Re-Normalisation Group) k-ε, and Reynolds-Stress[36]. The blade passage always accomplishes a frequently superior performance with the SST-TRANS model. Heat transfer at the turbine endwall by the secondary flow impacts was predicted accurately, using RANS (Reynolds-Averaged Navier-Stokes) and TRANS (Transitional) models[37-38]. On the 3D domain of the blade suction surface, the SST-TRANS model accomplishes very precisely and forecasts both the transition flow as well as the turbulent flow till the trailing edge continuously. The area of down mass transfer streaming parallel to the corner vortex is fairly well forecasted, visible in the Fig. 11 contour plot as an area colored in shades of blue and also in the Fig. 10 line plots as localized lower values, for x/Cax = 0.55-0.85. Striking adjacent to the suction surface, the augmentation of mass transfer owing to the corner vortex is caught. At the trailing edge downstream, the manifestations of unstable shedding of vortices are forecasted well.
2.2.2 Pitch-averaged film cooling effectivenessFor the film cooling advantage computation in respect of the whole surface of the endwall, two endwall contouring shapes at three BR are shown in Fig. 11. As the BR increases from 0.5 to 2.5, the endwall η rapidly increases for both endwall contouring shapes, because the horseshoe vortex is suppressed by the high momentum coolant. As the BR increases from 2.5 to 3.5, only a slight effect on endwall η is observed. The axisymmetric convergent contouring is beneficial for the endwall η, but the level of benefit is significantly affected by the BR. The level of benefit first increases then decreases with the increasing BR, and the maximum increase (69%) is noticed around the vane leading edge at design BR = 2.5.
2.2.3 High inflow turbulenceAs the pressure side core of the passage circulation is endwall distant, no enhancement of heat transfer takes place on the endwall, under the pressure side passage circulation(Fig. 13). A powerful pressure side horseshoe vortex (PHV) is accountable for the coefficients of enhanced heat transfer. The elevated St does not coexist with the pressure side horseshoe vortex core and is found in proximity to the suction surface. The major horseshoe vortex of the pressure side generates a few secondary vortices that affect the flow leading to the endwall might be the reason. An elevated band of St is seen above the horseshoe vortex and pressure side passage circulation (PPC) vortex and their coalescence moves the flow forward leading to the endwall. This interaction and the suction side corner vortex of the leading edge might be the reason for this elevated St. The coefficient of heat transfer is high as the horseshoe vortex is strong. The migration of the suction side corner vortex of the leading edge from the endwall enhances the elevated St location. The quantum of separation, as well as the rejoining, is very high. The present simulation forecasted the location area in respect of the elevated coefficient of heat transfer, adjacent to the endwall. As in the case of experimental reports, in the predictions of this study, a major secondary peak is also found farther from the endwall. The present study predicted the turbulence transition above the last portion of the suction surface well, similar to the previous studies concerning the midspan hydrodynamics and heat transfer simulations[19].
The numerical Sh distribution on the endwall is shown in Figs. 14 and 15. A slightly detectable horseshoe vortex moving through the passage is seen. Advancing downstream, the secondary flow repercussions are a little significant. The mass transfer enhancement by the influence of the corner vortex is expressed little including the shape of the valley originated. Shortly trailing edge vortex downstream, vortex shedding phenomena result in elevated rates of mass transfer. A precise forecast of the coefficients of mass transfer is resulted at the leading edge upstream by the model, SST-TRANS.
Pressure drops and temperature separation require consecutively finer LES grids. LES mesh resolution impacts for the hydrodynamics and the thermal exchange revealed an elevated sensitivity than RANS. Mesh-independent LES velocities required further analysis but revealed better results than the RANS was evident at the cross sections. LES was better for the boundary layer constituents at free-stream turbulence. The RANS is appropriate for the surface of the turbine reproducing flow attributes and appraising the efficiency of film cooling across the vane. Adjacent to the wall surfaces, at which surplus vortices are evident, RANS and LES differ in hydrodynamics, though these do not reflect predominantly in overall flow characteristics. No differences are noticed at the vane downstream, concerning these models.
The leading edge Sh improvement (Fig. 13) is shown at x/Cax = -0.015 quantitatively. The capture of the horseshoe vortex passing towards the adjacent blade showed its pressure side leg with its suction side leg. At the mid-passage location, the inclination is distinctive till the trailing edge, and the best results are shown in Fig. 15 line plots at x/Cax= 0.55 to 0.85.
3 ConclusionsA detailed turbine flow modeling at low(0.04%-0.2%) and high (4%-8%) turbulence intensities is performed concerning the heat transfer and hydrodynamics in 3-D throughout the optimization by numerical simulations with exit chord Re= 5×105. A counter-rotating circulation observed in the numerical predictions of the low (0.04%-0.2%) as well as high (4%-8%) inflow turbulence intensities get magnified while in passage flow and evolved as the passage vortex bulk. The main difference concerning the high inflow turbulence condition is the magnitude of reuniting area location prompted by the suction side leading edge corner vortex and could be due to the combination actions in respect of secondary vortices developed farther from the endwall and the suction side leading edge corner vortex.
The outcomes of the Taylor-Gortler vortices appear to be existing with the low (0.04%-0.2%) inflow turbulence intensity condition and do not exist with the high (4%-8%) inflow turbulence intensity condition. A relevant difference for the high (4%-8%) turbulence inflow is that the forecast of transition is a little upstream on the suction side and more instantaneous, in comparison to the location found in experiments. The Nu disruption among the top and bottom windows at the zone of overlap differs by up to 16%. The contoured geometries showed a 15.4%, 3.2%, and 2.7% reduction in endwall Nu than their respective flat geometries concerning no slot, with slot (no coolant) and upstream slot respectively. An outstanding lowering in endwall Nu(9% more than the contoured case and 23% more than the flat case) was attained owing to the sole existence of the upstream slot.
On the whole, the numerical prediction outcomes reveal heat transfer enhancement, as the Reθ-γ transition model is turned on. There is scope to investigate the distinctive endwalls, non-axisymmetrically contoured to recognize additionally, why shape transformations in these regions influence the aero-thermal characteristics of the passage.
| [1] |
Denton J D. Loss mechanics in turbomachines. Journal of Turbomachinery, 1993, 115(4): 621-656. DOI:10.1115/93-GT-435 (  0) 0) |
| [2] |
Dickel J A, Marks C, Clark L, et al. Non-axisymmetric endwall contouring of front-loaded high-lift low-pressure turbines. Proceedings of the 2018 AIAA Aerospace Sciences Meeting. Kissimmee: AIAA SciTech Forum, 2018. AIAA 2018-2125. DOI: 10.2514/6.2018-2125.
(  0) 0) |
| [3] |
Benton S I, Bons J P, Sondergaard R. Secondary flow loss reduction through blowing for a high-lift front-loaded low-pressure turbine cascade. Journal of Turbomachinery, 2013, 135(2): 021020. DOI:10.1115/1.4007531 (  0) 0) |
| [4] |
Arjun K S, Rakesh K, Tide P S. Passive downward heat transfer in reverse thermosyphon enabled bubble pump with two working media for U-tube solar thermal collector. Trends in Sciences, 2022, 19(20): 6234. DOI:10.48048/tis.2022.6234 (  0) 0) |
| [5] |
McQuilling M W. Design and Validation of a High-Lift Low-Pressure Turbine Blade. Dayton, OH: Wright State University. 2007. http://rave.ohiolink.edu/etdc/view?acc_num=wright1189792837.
(  0) 0) |
| [6] |
Langston L S. Secondary flows in axial turbines— A Review. Annals of New York Academy of Sciences, 2006, 934(1): 11-26. DOI:10.1111/j.1749-6632.2001.tb05839.x (  0) 0) |
| [7] |
Varty J W, Soma L W, Ames F E, et al. Vane suction surface heat transfer in regions of secondary flows: the influence of turbulence level, reynolds number, and the endwall boundary condition. Journal of Turbomachinery, 2018, 140(2): 021010. DOI:10.1115/1.4038281 (  0) 0) |
| [8] |
Ashworth D A, LaGraff J E, Schultz D L, et al. Unsteady aerodynamic and heat transfer processes in a transonic turbine stage. Journal of Engineering for Gas Turbines and Power, 1985, 107(4): 1022-1030. DOI:10.1115/1.3239806 (  0) 0) |
| [9] |
Dullenkopf K, Schulz A, Wittig S. The effect of incident wake conditions on the mean heat transfer of an airfoil. Proceedings of the International Gas Turbine and Aeroengine Congress and Exposition, Volume 4: Heat Transfer; Electric Power; Industrial and Cogeneration. Brussels, Belgium: American Society of Mechanical Engineers. Brussels, ASME. 1990. DOI: 10.1115/90-GT-121.
(  0) 0) |
| [10] |
Bu H, Guo Z, Song L, et al. Effects of cooling configurations on the aerothermal performance of a turbine endwall with jet impingement and film cooling. Journal of Turbomachinery, 2021, 143(6): 1-26. DOI:10.1115/1.4050358 (  0) 0) |
| [11] |
Bai B, Li Z, Li J, et al. The effects of axisymmetric convergent contouring and blowing ratio on endwall film cooling and vane pressure side surface phantom cooling performance. Journal of Engineering for Gas Turbines and Power, 2022, 144(2): 021020. DOI:10.1115/1.4052500 (  0) 0) |
| [12] |
Koschichow D, Frohlich J, Kirik I, et al. DNS of the flow near the endwall in a linear low pressure turbine cascade with periodically passing wakes. Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Volume 2D: Turbomachinery. Dusseldorf: ASME, 2014. DOI: 10.1115/GT2014-25071.
(  0) 0) |
| [13] |
Cui J, Nagabhushana Rao V, Tucker P G. Numerical investigation of secondary flows in a high-lift low-pressure turbine. International Journal of Heat and Fluid Flow, 2017, 63: 149-157. DOI:10.1016/j.ijheatfluidflow.2016.05.018 (  0) 0) |
| [14] |
Pichler R, Zhao Y, Sandberg R, et al. Large-eddy simulation and RANS analysis of the endwall flow in a linear low-pressure turbine cascade, part Ⅰ: flow and secondary vorticity fields under varying inlet condition. Journal of Turbomachinery, 2019, 141(12): 1-28. DOI:10.1115/1.4045080 (  0) 0) |
| [15] |
Bu H, Yang Y, Song L, et al. Improving the film cooling performance of a turbine endwall with multi-fidelity modeling considering conjugate heat transfer. Journal of Turbomachinery, 2022, 144(1): 011011. DOI:10.1115/1.4052018 (  0) 0) |
| [16] |
Wang C, Luo L, Wang L, et al. Experimental and numerical investigation of outlet guide vane and endwall heat transfer with various inlet flow angles. International Journal of Heat and Mass Transfer, 2016, 95: 355-367. DOI:10.1016/j.ijheatmasstransfer.2015.11.029 (  0) 0) |
| [17] |
Kanani Y, Acharya S, Ames F E. Large eddy simulation of bypass transition in vane passage with freestream turbulence. Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Volume 5B: Heat Transfer, 2019. GT2019-91099. DOI: 10.1115/GT2019-91099.
(  0) 0) |
| [18] |
Kanani Y, Acharya S, Ames F E. Large eddy simulation of the laminar heat transfer augmentation on the pressure side of a turbine vane under freestream turbulence. Journal of Turbomachinery, 2019, 141(4): 041004. DOI:10.1115/1.4041599 (  0) 0) |
| [19] |
Kanani Y, Acharya S, Ames F E. Numerical predictions of turbine cascade secondary flows and heat transfer with inflow turbulence. Proceedings of ASME Turbo Expo: Turbomachinery Technical Conference and Exposition, Volume 7B: Heat Transfer. New York: ASME, 2020. DOI: 10.1115/GT2020-15654.
(  0) 0) |
| [20] |
Choi W, Jung K J, Park J S. Characteristics of heat transfer on a turbine blade endwall under various inlet flow conditions. Experimental Heat Transfer, 2021, 34(7): 678-694. DOI:10.1080/08916152.2020.1811804 (  0) 0) |
| [21] |
Varty J W, Ames F E. Experimental heat transfer distributions over an aft loaded vane with a large leading edge at very high turbulence levels. Proceedings of the ASME International Mechanical Engineering Congress and Exposition. Volume 8: Heat Transfer and Thermal Engineering. New York: ASME, 2016. DOI: 10.1115/IMECE2016-67029.
(  0) 0) |
| [22] |
Yang X, Zhao Q, Wu H, et al. Heat transfer measurements of a turbine endwall with engine-representative freestream turbulence and inlet swirl. Experimental Heat Transfer, 2022, 35(5): 653-673. DOI:10.1080/08916152.2021.1933651 (  0) 0) |
| [23] |
Fluent. FLUENT User's Guide. New York: FLUENT Inc, 2003.
(  0) 0) |
| [24] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 (  0) 0) |
| [25] |
Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables part 1 - model formulation. Journal of Turbomachinery, 2006, 128: 413-422. DOI:10.1115/1.2184352 (  0) 0) |
| [26] |
Ames F E, Barbot P A, Wang C. Effects of aeroderivative combustor turbulence on endwall heat transfer distributions acquired in a linear vane cascade. Journal of Turbomachinery, 2003, 125(2): 210-220. DOI:10.1115/1.1559897 (  0) 0) |
| [27] |
Schlatter P, Orlu R, Li Q, et al. Turbulent boundary layers up to Reθ=2500 were studied through simulation and experiment. Physics of Fluids, 2009, 21(5): 051702. DOI:10.1063/1.3139294 (  0) 0) |
| [28] |
Jarrin N. Synthetic Inflow Boundary Conditions for the Numerical Simulation of Turbulence. Manchester: The University of Manchester, 2008. https://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.676725.
(  0) 0) |
| [29] |
Papa M. Experimental and numerical investigation of the heat/mass transfer in the hub endwall region of a turbine cascade. Rome : Univeristy of Rome 'Tor Vergata', 2005.
(  0) 0) |
| [30] |
Meng L, Zhang X D, Yan G, et al. Investigation of improving the hydraulic turbine cascade performance using non-axisymmetric endwall contouring. Advances in Mechanical Engineering, 2020, 12(4): 1-18. DOI:10.1177/1687814020915410 (  0) 0) |
| [31] |
Chen P, Zhao K, Li X, et al. Effects of varying non-axisymmetric contours of the turbine endwall on aerodynamics and heat transfer aspects: A sensitivity analysis study. International Journal of Thermal Sciences, 2020, 161: 106689. DOI:10.1016/j.ijthermalsci.2020.106689 (  0) 0) |
| [32] |
Song L, Guo Z, Li J, et al. Optimization and knowledge discovery of a three-dimensional parameterized vane with nonaxisymmetric endwall. Journal of Propulsion and Power, 2017, 34(8): 1-13. DOI:10.2514/1.B36014 (  0) 0) |
| [33] |
Goldstein R J, Cho H H. A review of mass transfer measurements using naphthalene sublimation. Experimental Thermal and Fluid Science, 1995, 10(4): 416-434. DOI:10.1016/0894-1777(94)00071-F (  0) 0) |
| [34] |
Wang H P, Olson S J, Goldstein R J, et al. Flow visualization in a linear turbine cascade of high performance turbine blades. Journal of Turbomachinery, 1997, 119(1): 1-8. DOI:10.1115/1.2841006 (  0) 0) |
| [35] |
Panchal K V, Abraham S, Ekkad S V, et al. Effect of endwall contouring on a transonic turbine blade passage: heat transfer performance. Journal of Turbomachinery, 2017, 139(1): 011009. DOI:10.1115/1.4034411 (  0) 0) |
| [36] |
Pasinato H D, Squires K D, Roy R P. Assessment of reynolds-averaged turbulence models for prediction of the flow and heat transfer in an inlet vane-endwall passage. Journal of Fluids Engineering, 2004, 126(3): 305-315. DOI:10.1115/1.1760535 (  0) 0) |
| [37] |
Papa F, Madanan U, Goldstein R J. Modeling and measurements of heat/mass transfer in a linear turbine cascade. Journal of Turbomachinery, 2017, 139(9): 091002. DOI:10.1115/1.4036106 (  0) 0) |
| [38] |
Lynch S. Three-dimensional boundary layer in a turbine blade passage. Journal of Propulsion and Power, 2017, 33(4): 954-963. DOI:10.2514/1.B36232 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


