2. Department of Information Technology, Panimalar Engineering College, Chennai 600123, India;
3. Information Technology Department, College of Computing and Information Sciences, University of Technology and Applied Sciences-Shinas 324, Sultanate of Oman;
4. Department of Information Technology and Security, College of Computer Science and Information Technology, Jazan University, Jazan 45142, Kingdom of Saudi Arabia
Throughout the centuries, agriculture has played a vital role in the growth of nations, impacting human energy production for nutritious foods. The agricultural cycle typically comprises three fundamental phases: planting, monitoring and maintenance, and harvesting, each involving a range of tasks. Planting involves crop selection, land preparation, irrigation arrangement, crop readiness, and seed planting. Subsequently, agriculture primarily focuses on monitoring and regulating crop development, encompassing time-dependent tasks such as continuous crop monitoring, fertilizer application, disease and vegetation assessment, and pest control[1]. The final and most crucial phase, harvesting, includes activities like crop harvesting, storage, fragmentation, and market sale.
Sequential Pattern Mining (SPM) stands as a fundamental data mining technique with wide-ranging real-world applications. It aims to identify sub-sequences and recurring features in sequential data[2]. However, it is a more complex task compared to other pattern mining processes, such as frequent pattern mining and association analysis, especially when handling substantial agricultural datasets. Consequently, recognizing sequential patterns in a synchronized or distributed computing system has become imperative for addressing these challenges.
Given its significance and potential impact on predictive capabilities, decomposition techniques warrant greater attention than most signal processing methods. One promising approach to enhance decomposition methods is the utilization of Empirical Mode Decomposition (EMD). EMD is relatively straightforward to grasp and apply, breaking down complex patterns into stationary sub-series known as Intrinsic Mode Functions (IMF) and a residual component that is simple to model[3]. To qualify as an IMF, two criteria must be met: (a) the average of the input signal and its constraints must be equal, and (b) the average of the IMF, determined by feature points and minima, must be zero at any point[3].
EMD, often referred to as empirical pattern decomposition, offers a data-driven method for dissecting intricate signals into manageable Intrinsic Mode Functions (IMFs). This breakdown is achieved by focusing on the local oscillations present in the spatial domain[4]. Intriguingly, IMFs within EMD contain distinctive data that can effectively capture underlying information. EMD has demonstrated its effectiveness in addressing diverse challenges, ranging from disease identification and landslide prediction to gas leak detection and financial sector forecasting.
Shifting to the realm of artificial intelligence, the Ant Colony Optimization (ACO) algorithm has gained significant prominence. It draws inspiration from the efficient route-finding behaviors of real-world ants. These insects excel in finding the shortest path and organizing their routes efficiently, serving as a model for the ACO algorithm. ACO is a recognized form of artificial intelligence employed for optimization, inspired by the navigational abilities of ants. Ants, with their innate ability to leave a scent trail, assist other ants in locating and following the shortest path. As a result, ACO represents one of the most advanced evolutionary algorithms, currently applied in agricultural technology. The selection of ACO in our study is motivated by its specific advantages in addressing combinatorial optimization problems, such as sequence pattern mining in the context of serial remote sensing images.
The proposed approach initially involves a pixel clustering technique to reduce the complexity of the original Serial Remote Sensing Images (SRSI) cropland dataset. It efficiently compresses SRSI pixel values by overlapping frames horizontally and grouping pixels with similar spatial patterns. This consolidates SRSI into a format that exclusively provides cluster data, and further consolidation of similar clusters reduces data redundancy. In the final phase, the ACO technique is extended to extract frequent patterns from clustered data, classifying clusters based on size and the frequency of sequence data they contain. This approach adapts the determination of sequence pattern assistance by considering the dimensions of clusters and mitigates computational complexity and time consumption through pixel clustering methods. The proposed technique enhances image quality, makes it more robust against image acquisition challenges, and yields highly reliable temporal features while achieving minimum support values. The main contributions of this study are given below:
1) This study introduces a unique approach to sequence pattern mining by combining EMD and ACO techniques, offering a fresh perspective in the field.
2) The integration of EMD and ACO enhances feature selection, leading to the extraction of essential characteristics from serial remote sensing images.
3) The study aims to provide a detailed comparison between two distinct methodologies used to generate sequence databases from experimental datasets: the direct method and the RLC-based pixel clustering approach. The dataset IDs, spanning from D1 to D8, represent various geographical regions and corresponding time intervals.
4) The proposed hybrid method is not only accurate but also computationally efficient, reducing time and cost requirements, making it suitable for the analysis of farmland datasets based on serial remote sensing images.
1 Related WorkSequential pattern mining stands as a pivotal data mining technique, wielding extensive real-world applications. Over time, researchers have consistently broadened and refined its methodologies and algorithms in a relentless pursuit of heightened efficacy. Notably, the incorporation of swarm intelligence and optimization techniques[5] has witnessed a surge in popularity across diverse domains in recent years, ushering in innovative solutions to intricate challenges.
An innovative approach known as SI-EDT was introduced by Darehnaei Ghasemi et al.[6] in their work. In this research, the application of swarm intelligence and deep transfer learning techniques for the detection of multiple vehicles within Unmanned Aerial Vehicle (UAV) images is explored. The synergistic potential of ensemble learning and deep transfer learning is harnessed by their methodology, ultimately leading to enhanced vehicle detection capabilities within aerial imagery.
Liu et al.[5] introduced a technique that involves the utilization of particle swarm optimization to enhance variational mode decomposition, with a specific focus on denoising ground-penetrating radar data. Through the integration of optimization techniques, the objective is to enhance the quality of radar data, rendering it valuable for diverse remote sensing applications.
Shokouhifar[7] placed its emphasis on the optimization of network function placement and routing through the amalgamation of ant colony optimization and fuzzy heuristics. The research tackles the intricate challenge of optimizing the joint placement and routing of virtual network functions, a matter of significance within the realm of virtual networks and cloud computing.
The introduction of a technique by Chen and Zheng[8] involves the integration of empirical mode decomposition and independent recurrent neural networks for the prediction of air quality indices. This research represents a significant contribution to the realm of air quality forecasting, a crucial component of environmental monitoring and public health.
The dynamic nature of data mining and its applicability across various domains is exemplified by recent advancements in swarm intelligence, optimization techniques, and data decomposition methods. These techniques are progressively being employed to tackle intricate challenges in areas such as image analysis, data denoising, network optimization, and environmental prediction[9]. SPM focuses on the locations and internal spatial connections of occurrences, while also addressing procedural or content-related data. EMD is suggested[3] for energetic noise-assisted data mining, particularly in the context of nonlinear and non-stationary pattern information. EMD requires that the data exhibits a simple inherent pattern of fluctuations. It offers a data-driven approach to break down complex patterns into restricted IMF based on local oscillations in the external world. Each IMF reflects unique data related to the original patterns[10]. This method involves identifying local peak positions, both positive and negative, to generate IMF, with the original time series subtracted from the IMF displaying the highest volatility. The information removed from each IMF also appears in subsequent IMF. When used correctly, the sum of all IMF and residual data should closely match the original data[11].
The ACO algorithm is gaining increasing prominence in agricultural applications. One of the studies by Shokouhifar[7] illustrates how ACO is utilized for route optimization in agricultural environments. Additionally, Cao and colleagues[1] explored the maintenance of agricultural equipment and proposed an ACO model as a framework for pattern mining. ACO optimization is highlighted as a critical tool for enhancing the efficiency of various farming practices. Jiang and his team[9] introduced an optimization technique for autonomous farming machinery using the ACO method, demonstrating how ACO can be employed to design optimal paths for agricultural robots, circumventing obstacles and ultimately saving time and money in agricultural production. Mythili and colleagues[11] discussed the utilization of ACO for optimization in agricultural contexts, particularly in optimizing routing signals and the significance of trained parameters in agricultural crop yield systems.
2 Proposed WorkThe research presents a sequential pattern mining method that leverages pixel clustering. The primary objective of this technique is to exploit the fact that adjacent pixels reliably exhibit the same frequent patterns. By organizing pixels into groups that share similar patterns, it becomes unnecessary to process every individual pixel. The proposed approach involves two main phases. In the initial phase, researchers introduce the concept of pixel grouping, which lays the foundation for the subsequent steps. Following this, researchers detail a method for grouping pixels based on EMD. EMD is applied to break down the serial remote sensing images into several relatively stationary sub-series known as IMF and residues, making them easier to analyze as shown in Fig. 1.

|
Fig.1 Overview of proposed work |
To qualify as an IMF, certain criteria must be met: (ⅰ) the total value of a maxima and the total value of the input signal must be approximately equal, differing by no more than one; and (ⅱ) the average of the IMF, determined by regional maxima and minima, should remain close to zero at all times[3]. The overall workflow for implementing EMD in this research is illustrated in Fig. 1, with the EMD computation process explained accordingly. This innovative methodology streamlines the analysis of serial remote sensing images by reducing the computational load through pixel clustering and optimizing the decomposition process using EMD. Additionally, the application of ant colony optimization in the final phase of the workflow aids in identifying sequential patterns, ultimately offering a comprehensive solution to complex data analysis challenges.
| $\operatorname{SRSI}(t)=\sum\limits_{i=1}^n\left(S_i(t)+\operatorname{Res}_n(t)\right)$ | (1) |
The utilization of the EMD approach is essential for separating patterns from the images, especially when there are limitations in the maximum spectral region. EMD proves to be an efficient and straightforward method for achieving this goal. It is worth noting that each IMF possesses the capability to capture various features of the data. As pointed out by Refs. [12-15], adopting a strategic approach underscoring the importance of efficient techniques like EMD in such scenarios.
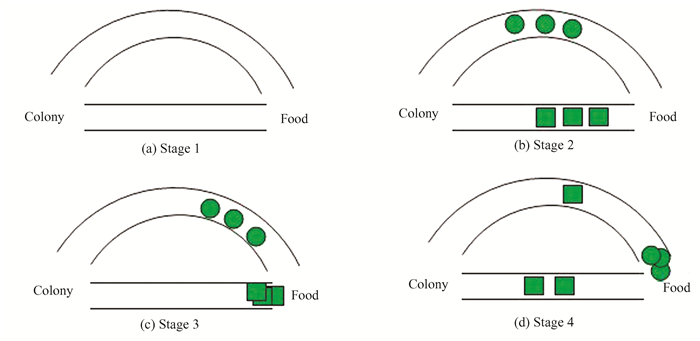
The fundamental principle underlying the Ant Colony Optimization (ACO) algorithm is to mimic the behavior of ants as they leave their nests in search of food, aiming to find the shortest path to their destination[16-18]. The ACO algorithm operates in several stages, closely resembling the natural foraging behavior of ants as shown in Fig. 2.
|
Fig.2 Overall behavior of ACO |
Stage 1: All ants are situated within their nest at the beginning of the process. At this point, there is no pheromone content present in the environment. The environment is essentially unexplored, and the ants are unaware of the optimal path.
Stage 2: Ants initiate their food forage, and they distribute themselves evenly among various potential paths with equal probabilities (e.g., 0.5 probability for each path). In the illustration, it is clear that the curved path is longer compared to the straight path. Consequently, the time it takes for ants to reach the food source along the curved path is greater than the straight path.
Stage 3: As ants explore the environment, they eventually discover the shorter path, which allows them to reach the food source more quickly. At this stage, ants face a decision-making challenge. Since a pheromone trail now exists along the shorter path, the probability of selecting the shortest path becomes higher compared to the curved path.
Stage 4: When more ants came through the shorter path, the concentration of pheromones along that path increases. Simultaneously, the pheromone concentration on the curved path decreases over time due to natural evaporation. As the pheromone concentration on the curved path diminishes, the probability of selecting this path in subsequent stages decreases as well.
Consequently, the entire ant colony predominantly uses the shorter path, driven by the higher selection probabilities. Ultimately, this dynamic process of pheromone deposition and evaporation leads to path optimization.
The ACO algorithm, inspired by the collective intelligence of ants, is a powerful optimization technique used in various applications to find optimal solutions for complex problems, especially those related to path-finding and routing.
Ant colony optimization-based decomposition implements two algorithms for the ant movement. The algorithms are as follows:
Algorithm 1:
Sequential pattern mining with pixel clustering, EMD, and ACO.
Input:
Serial Remote Sensing Images (SRSI) dataset over time, denoted as SRSI(t).
Output:
Extracted sequential patterns.
Method:
1) Pixel clustering:
·Exploit the consistent patterns among adjacent pixels.
·Organize pixels into groups with similar patterns to reduce computational load.
2) Empirical Mode Decomposition (EMD):
·Break down SRSI into relatively stationary sub-series called Intrinsic Mode Functions (IMF) and residues using EMD.
·Ensure each IMF meets specific criteria, including the equality of maxima and input signal total values and an average close to zero determined by regional maxima and minima.
3) Pixel grouping with EMD:
·Group pixels based on the decomposed IMFs and residues.
·Establish pixel clusters to represent similar spatial patterns.
4) Ant Colony Optimization (ACO):
·Imitate ant foraging behavior to optimize sequential pattern identification.
·Utilize ACO algorithm in the final phase of the workflow.
·Implement stages mimicking ant behavior, including exploration, path distribution, discovery of optimal paths, and path optimization.
5) Sequential pattern identification: Represent SRSI using the following equation
| $\operatorname{SRSI}(t)=\sum\limits_{i=1}^n\left(S_i(t)+\operatorname{Res}_n(t)\right)$ |
·Apply ACO to identify sequential patterns based on the optimized pixel clusters.
6) Output:
Obtain extracted sequential patterns reflecting changes and growth in the specified geographic area over time.
Algorithm 2:
Ant colony optimization-based multilinear matrix decomposition
Input: Multilinear matrix M
Output: Decomposed matrices U, V, and W
1) Initialization:
a. Parameters such as the number of ants, iterations, and pheromone evaporation rate are defined.
b. Pheromone matrices P_U, P_V, and P_W are initialized with small positive values.
c. Matrices U, V, and W are initialized with non-negative values in a random manner.
2) Ant movement: For each ant
ⅰ. A path for each matrix factorization (U, V, W) is initialized.
ⅱ. Elements of U, V, and W matrices are traversed based on pheromone concentrations.
ⅲ. Pheromone concentrations on visited elements are updated.
3) Update matrices:
a. Matrices U, V, and W are updated based on ant paths.
b. Ant paths are used to adjust factorized matrices for improved decomposition.
4) Pheromone update:
a. Pheromone on all matrix elements is evaporated using the evaporation rate.
b. Pheromone on elements visited by ants is deposited, proportionate to solution quality.
5) Convergence check:
a. Convergence criteria (e.g., maximum iterations are checked).
b. If convergence is achieved, the algorithm is exited; otherwise, proceed to 2).
6) Output:
Decomposed matrices U, V, and W are returned.
End
The work seamlessly integrates the proposed algorithms for extracting sequential patterns from the SRSI dataset over time. The initial step, Algorithm 1 commences with pixel clustering, utilizing consistent patterns among neighboring pixels to efficiently organize them into groups sharing similar patterns. This strategic grouping significantly reduces the computational load. Subsequently, EMD is applied to disassemble the SRSI into relatively stationary sub-series known as IMF and residues. Pixel grouping with EMD refines this process by further organizing pixels based on the decomposed IMFs and residues, creating pixel clusters that represent similar spatial patterns. The final stage incorporates the ACO algorithm, which emulates ant foraging behavior to optimize the identification of sequential patterns. This involves various stages such as exploration, path distribution, discovery of optimal paths, and path optimization. The resulting sequential patterns capture changes and growth in the specified geographic area over time.
Algorithm 2 delineates the systematic process of breaking down a given multilinear matrix M into matrices U, V, and W. The algorithm initiates by defining parameters, pheromone matrices, and initializing factorized matrices. Ant movement guides the traversal of matrix elements based on pheromone concentrations, updating concentrations on visited elements. The update matrices step refines matrices U, V, and W based on ant paths, enhancing the decomposition process. Pheromone update involves evaporation and deposition of pheromones, and convergence check ensures convergence criteria are met. The algorithm iterates until convergence, culminating in the output of decomposed matrices U, V, and W. Collectively, these algorithms form a robust and inclusive methodology for extracting profound patterns and insights from intricate remote sensing datasets.
3 Performance AnalysisThis article assesses the efficacy of the proposed methodology and presents the obtained results. The algorithm's performance is evaluated using a dataset collection related to cropland. The SRSI in this study depict the conditions of the land surfaces in Iowa, covering an extensive area of approximately 150000 km2. Each pixel in the SRSI images represents an area of 900 m2, and these images are utilized to depict various agricultural crop types in the area, with each crop type being distinguishable by its corresponding color on the chart. The data extracted from these SRSI images is divided into four specific time intervals, which are labeled as D1, D2, D3, D4, D5, D6, D7, and D8, as elaborated in Table 1.
| Table 1 Summary of datasets used in the study |
In this research, we carried out a comprehensive analysis using a various set of datasets, each characterized by its unique features. These datasets cover the period from 2010 to 2021 and encompass various geographical regions, including the Eastern Farmland Region, Northern Woodlands, Region of ASD 1910, Region of IOWA state, Regions of Butler Country, Smaller portion of Butler Country, Southern Plains Region, and Western Coastal Area. The pixel counts for these datasets exhibit substantial variation, ranging from 21×132 pixels for the smaller portion of Butler country to 17795×11671 pixels for the Region of IOWA state. These datasets served as a valuable source of information for our study, enabling the effective application of the innovative EMD and ACO methodology. The diversity in regions and pixel counts allowed us to demonstrate the versatility of our approach across different scenarios, such as urbanization, native vegetation expansion, and agricultural activities. The decomposition of the images is achieved through EMD, as illustrated in Fig. 3. Subsequently, an analysis is conducted to demonstrate the effectiveness of the proposed system and strategy. The obtained results are then compared with traditional approaches to highlight the advantages of the recommended method.

|
Fig.3 (a) Input image (b) EMD image |
The presented approach is precisely crafted to augment the effectiveness of extracting spatial sequential patterns from raster SRSI through the implementation of a pixel grouping strategy. The algorithm computes pattern features through a transformative process, streamlining multilinear matrix decomposition via covariance estimation and identification of orthogonal components within the image. The matrix decomposition, guided by ACO, is orchestrated through a run-length encoding process (RLC). This advanced compression methodology ensures a robust preservation of information, especially in non-repeated pixel-based methodologies, safeguarding both structural and textural intricacies. Comparative scrutiny against existing techniques substantiates the superior efficiency of the proposed system. The observed outcomes underscore the efficacy of the ACO-enhanced system in effectively addressing conventional challenges inherent in SRSI images.
By conducting this comparison and estimation, the article seeks to underscore the superior performance of the proposed methodology in contrast to existing techniques, thus showcasing its potential for application in the field of cropland analysis.
The result provided in Table 2 provides a detailed comparison between two distinct methodologies employed in generating sequence databases from experimental datasets: the direct method and the RLC-based pixel clustering approach. The dataset IDs, ranging from D1 to D8, delineate various geographical regions and corresponding time intervals.
In Table 2, Produce directly (DV, RowNum) delineates the data volume (DV) and the number of rows (RowNum) in the sequence database directly derived from the experimental datasets. The data volume is quantified in either megabytes (MB) or gigabytes (GB), contingent upon the dataset's size. The data volume and the number of rows of RLC-based Pixel Clustering (DV, RowNum) are presented for the sequence database generated through the RLC-based pixel clustering method. This innovative approach utilizes run-length encoding to cluster pixels, thereby diminishing the overall size of the sequence database. The compression ratio is computed by juxtaposing the number of rows between the direct method and the RLC-based pixel clustering technique as in Table 2. It signifies the percentage decrease in the number of rows achieved by aggregating pixels into distinct groups.
| Table 2 Comparison of sequence databases produced by RLC-based pixel clustering and the direct method |
The RLC-based pixel clustering method accomplished an impressive compression ratio of 94.37%, denoting a substantial reduction in the number of rows when compared to the direct method. This compression proves advantageous for efficient sequential pattern mining. The RLC-based pixel clustering method excelled, boasting a remarkable compression ratio of 99.36%. This signifies a noteworthy decrease in the number of rows, augmenting the efficiency of pattern mining. The compression ratio for D3 reached 99.75%, underscoring the efficacy of the RLC-based pixel clustering method in reducing the dataset's size while preserving crucial information. Similar to D2, D4 exhibited a high compression ratio of 99.85%, signifying a significant reduction in the number of rows and contributing to efficient sequential pattern mining. Despite a slightly lower compression ratio of 92.71%, the RLC-based pixel clustering method demonstrated noteworthy efficiency in downsizing the dataset. The compression ratio for D6 was 95.00%, indicating a substantial reduction in the number of rows through pixel clustering, enhancing the efficiency of sequential pattern mining. The compression ratio for D7 stood at 92.17%, showcasing the effectiveness of the RLC-based pixel clustering method in reducing the dataset size for improved pattern mining. With a compression ratio of 96.39%, the RLC-based pixel clustering method efficiently reduced the dataset size, demonstrating its effectiveness across diverse datasets.
4 ConclusionsThis research presents a novel approach to sequence pattern mining by integrating EMD and ACO techniques. The combined use of EMD and ACO enhances feature selection, facilitating the extraction of crucial characteristics from serial remote sensing images with increased precision and specificity. Our results highlight a significant enhancement in the efficiency of sequential pattern mining through the application of this innovative hybrid method, seamlessly combining EMD and ACO for feature selection. Importantly, the proposed method demonstrates accuracy and computational efficiency, leading to reduced time and cost requirements. The study emphasizes the potential of this inventive methodology, especially in the domains of urbanization, native vegetation expansion, and agricultural activities. The validation of our methodologies using datasets from the Cropland Data Layer serves to confirm the efficacy of our approach in generating precise patterns with computational efficiency.
| [1] |
Cao R, Li S, Ji Y, et al. Task assignment of multiple agricultural machinery cooperation based on improved ant colony algorithm. Computers and Electronics in Agriculture, 2021, 182(C): 105993. DOI:10.1016/j.compag.2021.105993 (  0) 0) |
| [2] |
Cao L, Dong X, Zheng Z, et al. Efficient negative sequential pattern mining. Artificial Intelligence, 2016, 235: 156-182(c): 105993. DOI:10.1016/j.artint.2016.03.001 (  0) 0) |
| [3] |
Dai Z, Zhu H. Forecasting stock market returns by combining sum-of-the-parts and ensemble empirical mode decomposition. Applied Economics, 2020, 52(21): 2309-2323. DOI:10.1080/00036846.2019.1688244 (  0) 0) |
| [4] |
Du H, Song D, Chen Z, et al. Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method. Journal of Cleaner Production, 2020, 270: 122248. DOI:10.1016/j.jclepro.2020.122248 (  0) 0) |
| [5] |
Liu S, Chen Y, Luo C, et al. Particle swarm optimization-based variational mode decomposition for ground penetrating radar data denoising. Remote Sensing, 2022, 14(13): 2973. DOI:10.3390/rs14132973 (  0) 0) |
| [6] |
Darehnaei Ghasemi Z, Shokouhifar M, Yazdanjouei H, et al. SI-EDTL: swarm intelligence ensemble deep transfer learning for multiple vehicle detection in UAV images. Concurrency and Computation: Practice and Experience, 2022, 34(5): e6726. DOI:10.1002/cpe.6726 (  0) 0) |
| [7] |
Shokouhifar M. FH-ACO: Fuzzy heuristic-based ant colony optimization for joint virtual network function placement and routing. Applied Soft Computing, 2021, 107: 107401. DOI:10.1016/j.asoc.2021.107401 (  0) 0) |
| [8] |
Chen S, Zheng L. Complementary ensemble empirical mode decomposition and independent recurrent neural network model for predicting air quality index. Applied Soft Computing, 2022, 131: 109757. DOI:10.1016/j.asoc.2022.109757 (  0) 0) |
| [9] |
Jiang Z, Zhou M, Tong J, et al. Comparing an ant colony algorithm with a genetic algorithm for replugging tour planning of seedling transplanter. Computers and Electronics in Agriculture, 2015, 113: 225-233. DOI:10.1016/j.compag.2015.02.011 (  0) 0) |
| [10] |
Mostafiz R, Rahman M M, Uddin M S. Gastrointestinal polyp classification through empirical mode decomposition and neural features. SN Applied Sciences, 2020, 2: 1143. DOI:10.1007/s42452-020-2944-4 (  0) 0) |
| [11] |
Mythili K, Rangaraj R. Crop recommendation for better crop yield for precision agriculture using ant colony optimization with deep learning method. Annals of the Romanian Society for Cell Biology, 2021, 25(4): 4783-4794. (  0) 0) |
| [12] |
Peng Z K, Tse P W, Chu F L. An improved Hilbert-Huang transform and its application in vibration signal analysis. Journal of Sound and Vibration, 2005, 286(1-2): 187-205. DOI:10.1016/j.jsv.2004.10.005 (  0) 0) |
| [13] |
Xu C, Du S, Gong P, et al. An improved method for pipeline leakage localization with a single sensor based on modal acoustic emission and empirical mode decomposition with hilbert transform. IEEE Sensors Journal, 2020, 20(10): 5480-5491. DOI:10.1109/JSEN.2020.2971854 (  0) 0) |
| [14] |
Mohammad N, Muad A M, Ahmad R, et al. Accuracy of advanced deep learning with tensorflow and keras for classifying teeth developmental stages in digital panoramic imaging. BMC Medical Imaging, 2022, 22(1): Article number 66. DOI:10.1186/s12880-022-00794-6 (  0) 0) |
| [15] |
Na J, Ding H, Zhao W, et al. Pfeifer Object-based large-scale terrain classification combined with segmentation optimization and terrain features: A case study in China. Trans. GIS, 2021, 25(6): 2939-2962. (  0) 0) |
| [16] |
Pastorino M, Moser G, Serpico S, et al. Semantic segmentation of remote sensing images through fully convolutional neural networks and hierarchical probabilistic graphical models. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-16. DOI:10.1109/TGRS.2022.3141996 (  0) 0) |
| [17] |
Ruiz L F C, Guasselli L A, Simioni J P D, et al. Object-based classification of vegetation species in a subtropical wetland using Sentinel-1 and Sentinel-2A images. Science of Remote Sensing, 2021, 3(7): 100017. DOI:10.1016/j.srs.2021.100017 (  0) 0) |
| [18] |
Sosa-Rey F, Abderrafai Y, Lewis A D, et al. Open-source segmentation of individual fibers and porosity in tomographic scans of additively manufactured short fiber reinforced composites. Composites Science and Technology, 2022, 226: 109497. DOI:10.1016/j.compscitech.2022.109497 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


