In order to generate electricity, the light coming from the sun has been utilized by Semiconductor solar cells. The main element in solar cells, that collects the photons that the sun's beams transfer, is silicon[1-5]. With the added benefits of being compact and affordable, solar cells are able to produce more energy than some other traditional sources. The same manufacturing and processing procedures as for computer memory chips are used to create them. In this study, simulation of solar cell is proposed with variation in semiconductor parameters such as physical, fundamental and environmental[6-10]. Along with genetic algorithm is also presented to simulate and achieve optimal solar cells parameters. Throughout this work, various semiconductors will be observed, and it will be necessary to identify factors like material, temperature, etc. To determine the best level of PV prototype tolerance for abnormal factors that affect semiconductors, genetic algorithms are going to be added[11]. As a result, the PV model performance will be improved[1].
Light energy can be converted into electrical energy with the use of photovoltaic effect by solar cells—also known as photovoltaic cells. Solar energy systems, in contrast to batteries, do not rely on chemical reactions, nor do they require fuel to operate[12-15]. In addition to this, unlike electrical generators, solar cells do not have any moving parts[2]. While residential solar panels only convert about 20% of the sunshine they collect into usable electricity, commercial solar panels can convert as much as 40% of the sunlight they receive. On the other hand, it is anticipated that as technology continues to improve, the solar panels' efficiency will increase[3]. The majority of them are silicon cells that come in many varieties with distinct conversion costs as well as efficiencies, ranging from non-crystalline amorphous silicon cells to polycrystalline and monocrystalline (single crystal) silicon cells. In order to turn sunlight into electricity for universal use in industrial and commercial as well as home settings, solar farms can be constructed. Arrays, the biggest structure of solar cells, are made up of thousands of individual cells[16].
A Solar cells structure is shown in Fig. 1. Solar cells are unable to generate energy unless they are first exposed to light, and then must be able to process that light[17-22]. The majority of cells are only able to convert between 10% and 20% of the energy they absorb into usable power, whereas the laboratory cells that have been shown to be the most efficient can reach up to 45% efficiency under ideal conditions[20]. Photons that fall outside of this band are lost. In addition, there are certain photons within the frequency range that do not have the necessary amount of energy to form electrons, while there are other photons that have an excessive amount of energy and the excess is lost[23-28]. The reason for this is that solar cells are designed to be as efficient as possible by only capturing photons that fall within a specific frequency band. Real-world issues such as panel construction, alignment, location, heat, shadows, along with lack of cleanliness can all limit the optimum effectiveness of solar panels that cause the majority of real-world solar panels to only achieve between 10% and 20% of their potential[29-31]. This overall solar cell efficiency is determined by a mixture of several different types of efficiency, including charge carrier separation efficiency reflectance efficiency, conductive efficiency, as well as thermodynamic efficiency[32-34].
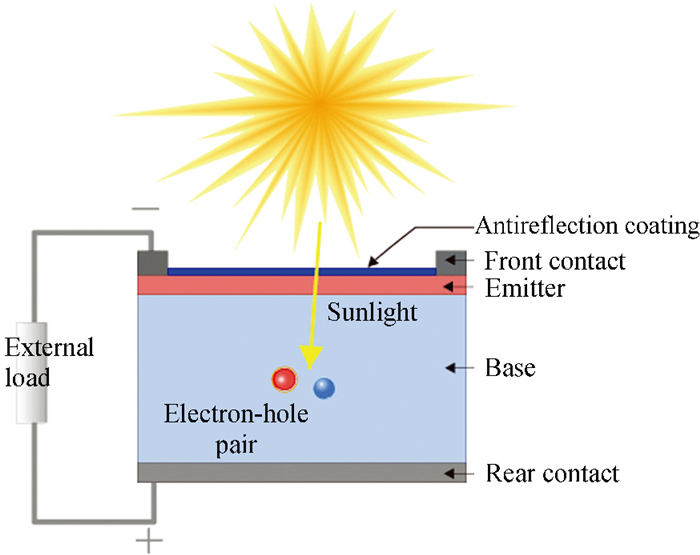
|
Fig.1 Solar cell① |
①Source: https://www.pveducation.org/pvcdrom/solar-cell-operation/solar-cell-structur
The majority of today's solar cells use semiconductor materials for the majority of the processes that take place in the cell, including the photons absorption that leads to the charge carrier's formation, as well as the subsequent separation of the photo-generated charge carriers. As a result, the semiconductor layers make up the most essential components of a solar cell; in fact, they are considered to be the solar cell's beating heart. There is a wide variety of semiconductor materials that can be used for the process of transforming the energy of photons into the energy of electrons, and each of these materials has its own set of benefits and limitations[35].
1 Literature ReviewHysa et al.[5] demonstrated how to simulate photovoltaic cells. Finding the nonlinear characteristics curves for power versus voltage as well as current versus voltage for solar cells was the primary objective of this research. The results of the simulation showed us that the output of photovoltaic cells varies with changes in irradiation, temperature, and certain physical parameters such as shunt resistance and series resistance. These changes also affect the amount of voltage, current as well as power that is produced. According to the research findings, increased values of the series resistance Rs result in a decrease in the power output of solar cells.
A summary of the numerous electronic phenomena that exist in polycrystalline thin solar cells but do not exist in conventional crystalline Si solar cells had been suggested by Burgelman et al.[6] in their publication. In the author's institute, a numerical simulation tool for solar cells called SCAPS was developed. The author, in this article describes how SCAPS treats these impacts statistically.
Ouédraogo et al.[7] examined how a polycrystalline silicon solar cell's total conversion efficiency and the connection between each energetic process as well as temperature (such as absorption, thermalization, thermodynamics, and fill factor) in a temperature range of 10-50 ℃. When compared to a rise in temperature, each of these separate efficiencies results in a decrease in temperature. In contrast to the thermalization as well as absorption efficiencies, the fill factor as well as the thermodynamic efficiency are more sensitive to a rise in temperature.
Detailed analysis of the two-dimensional (2-D) numerical modeling as well as circuit simulation has been given by Kuhlmann et al.[15] for the three-dimensional structure of previously developed MIS-IL cells. A good agreement between experimental as well as simulated current-voltage (Ⅰ-Ⅴ) characteristics has been generated using device parameters that were established through experimentation. As a result, resistive and recombinative losses might be determined spatially. In addition, optimization research has been considered for determining the highest amount of energy that can be extracted from MIS-IL silicon solar cells.
The research on silicon wafer solar cell Cu(In1-x, Gax)Se2 (CIGS) has been done. These studies were carried out by Song et al.[16]. Several other graded band-gap structures are investigated, includes twofold grading of the CIGS absorber layer, back surface area grading, and charge carrier region (SCR) grading. Analyses were done on the device's mechanics as well as the performance parameters for a variety of band-gap profiles. On the basis of the outcomes of the simulation, a graded band-gap configuration that is best for the CIGS solar cell is proposed here.
An optical model was presented by Fell et al.[17], which provides a computationally rapid alternative or extension to ray tracing. The model was developed for use in solar cell device simulations. It has been shown that the model might be used for accurate prediction of the optical features of high efficiency laboratory solar cells with two different temperatures as well as thicknesses. As a result, it is favorable to simplify and accelerate optical modeling as opposed to ray tracing alone, without significantly introducing inaccuracies for features that are typical of silicon solar cells.
All the uncertainties linked with the silicon solar cells' simulated efficiency have been addressed by Wasmer[18]. The uncertainty of the fundamental physical models is the cause of these uncertainties. Adapt their parameters in light of the principal measurement information. Then, they utilized an approach that combines metamodeling and Monte Carlo simulation to analyze how these parameters impact the simulated efficiency of solar cell systems. Moreover, demonstrate that the existence of a high space charge area at a recombining surface prevents Schenk's BGN model from accurately simulating the observed results. The existence of these differences demonstrates the importance of conducting additional research on the models in question. It has been found that alleviating diffused regions on textured surfaces to a planar geometry can result in an inaccuracy of up to 0.08% abs.
A geometric optical model was offered by Liu et al.[19] to represent the surfaces of monocrystalline silicon wafers that had undergone alkaline Saw-Damage Etched (SDE). An experimental examination was conducted on the optical characteristics of alkaline SDE surfaces with the utilization of monocrystalline silicon wafers. They discovered that this SDE surface representation can forecast transmission as well as reflection with an equivalent current density Root Mean Square Error (RMSE) range between 0.19 and 0.57 mA/cm2. The characteristic angle that was measured was 22°, and the planar fraction was either 0.25 or 0.36. In addition, the created model is utilized for the estimation of the optical loss in aluminum local back surface field (Al-LBSF) solar cells that have a Surface Deposition Epitaxial (SDE) rear surface.
Li et al.[20] proposed models along with a set of matching parameters for use in the process simulation of BBr3 tube diffusion in order to utilize the Sentaurus TCAD with solar cell applications. These models and parameters may be found in the article. The findings of simulations are contrasted with experimentally acquired doping profiles that were obtained using a wide variety of diffusion recipes. In order to emphasize the crucial process factors that influence the boron distribution profile and how it affects electrical performance, the scientists also carried out a process parameter sensitivity analysis.
Soeriyadi et al.[21] discussed a method that can directly and simultaneously retrieve sub-cell characteristics from tandem structures. The current-limiting cell can be correctly detected under various illuminant spectra, which influences the overall power performance based on the various current-voltage characteristics of the sub cells. In addition, on a GaAsP/SiGe tandem solar cell produced on a Si substrate, a three-terminal analysis was performed on the cell.
Many adjustments are necessary to alleviate recombination losses. The simulation model presented by Felmann et al.[2] is a useful tool for changing the rear-side dimensions and optimizing the diffusion profiles of back-contacted back-junction silicon solar cells.
This voltage shift may be a property of SHJ solar cells, according to Chavali et al.[8], who demonstrated that this behavior emerges from the heterojunction (HJ) and its associated carrier-transport barriers, that is inherent to SHJ devices. The authors investigate the entire current-voltage (J-V) characteristics under a range of lighting and temperature conditions in the surrounding environment utilizing numerical simulations.
A number of deviations from perfection were found by Brammertz et al.[9]. They also evaluated a variety of nonidealities present in Cu2ZnSnSe4 -CdS-ZnO solar cells with a conversion efficiency of 9.7% in order to determine what it is that is preventing these devices from functioning to their full potential. The devices also include potential fluctuations, but it does not seem like they substantially degrade their performance. As a result of increased recombination brought on by band tail defects, they most likely have the impact of reducing the minority carrier's lifetime.
Paretkar et al.[10] provided an estimation of the silver busbar's mechanical properties. The simulation's findings also show that the peel force rises steadily in proportion to the modeled work of adhesion, peaking at intermediate levels of the silver yield strength.
The relative change in system efficiency that occurs when moving from 55% to 90% of the light's original intensity being directed toward the Cu2O cell is less than 10%. Berney Needlemann et al.[11] investigated a system that utilizes crystalline silicon (Si) as well as cuprous oxide (Cu2O) as absorbers. According to the research, system requires a spectrum fidelity of the light which is directed to the Si cell that is better than 90% in order to surpass a high-efficiency single-junction Si device. Under certain circumstances, elevating this light's fidelity may result in a decrease in the system's effectiveness. Findings show that spatial variation on length scales ranging between 600 m and 4.8 mm has no significant influence on devices with emitter sheet resistances of < 500.
In order to allow for the calculation of the characteristics of the cell with relation to variations on environmental parameters like temperature and irradiance, Asim et al.[12] created a simulation model based on five parameters for a PV cell/array. This ultimately results in characteristics that exhibit nonlinearities. The shadow cast by solar photovoltaic arrays can have a variety of unintended consequences. Therefore, research into the matter is highly vital in order to discover and suggest techniques and measures that may be performed to go around this problem. Under conditions of partial shade, two solar PV modules consisting of two cells each are built for evaluation and simulation; these modules demonstrate great correspondence with one another.
The single-diode model, that is absolutely ideal, the single-diode Rests model, the single-diode RpRp model, the two-diode model, and the three-diode model were all presented by Sarkar et al.[13].In conclusion, it has been demonstrated that an enhancement in cell's operating temperature causes a decrease in open-circuit voltage and fill factor, as well as a considerable decline in performance.
Liu et al.[22] developed a stoichiometric etching strategy using ionic liquids to improve the performance of defective perovskite films in photovoltaic applications. The etching process removed defects and exposed a high-quality perovskite surface, resulting in a record power conversion efficiency of 17.51% and an open-circuit voltage of 1.37 V.
Li et al.[23] investigated the halide diffusion equilibrium at the heterointerface of perovskite solar cells (PSCs). They found that halide components diffuse from the perovskite layer to the fullerene layer, leading to nonstoichiometric perovskite surfaces and chemically doped transport layers. To address this issue, they developed a predoping strategy to achieve halide diffusion equilibrium during device fabrication. This approach resulted in stable power output and an efficiency of 23.13% under continuous one sun illumination.
Hao et al.[28] introduced the concept of a hybrid photon-enhanced thermionic emission converter and photovoltaic (PETE-PV) solar cell, which utilizes solar photons for both photovoltaic conversion and thermionic emission. Experimental results showed increased cathode saturation current and reduced cathode work function. Callies et al.[29] focused on optimizing perovskite-silicon tandem solar cells by evaluating different structures at the air-perovskite and perovskite-silicon interfaces. The evaluated structures reduced reflection losses and decreased thermalization losses by enhancing absorptance in the perovskite sub-cell near the bandgap. The best combination of structures led to a significant reduction in reflection loss and a 4.9% relative increase in efficiency. The suggested nanostructured approach showed potential benefits for reducing thermalization losses while achieving similar reflectance reduction.Some of the critical analysis is presented in Table 1.
| Table 1 Critical analysis of existing literature |
2 Critical Factors Affecting Solar Cell Performance
The photovoltaic cells performance gets affected by a wide variety of parameters and factors, comprising the contacts, the materials that make up the interfaces, the cooling, the internal parameters, the conditions of the environment, and materials, the sizes, and the geometry of the cells. A bibliometric analysis was performed using the search terms "Effect of Temperature on Solar Cell", "Effect of Irradiance on Solar Cell", and "Effect of Design on Solar Cell" to determine these factors. The graphs depicting the number of documents produced each year can be found in Figs. 2-4. According to the graph, it can be seen that beginning in 2010 and continuing up to the present day, the majority of the researchers' attention has been directed toward analysing how temperature, irradiance, and cell design interact. Since the PV system relies on commercial photovoltaic cells, the effectiveness of the two parts is considered by the temperature, irradiance, and geometry of the cells.
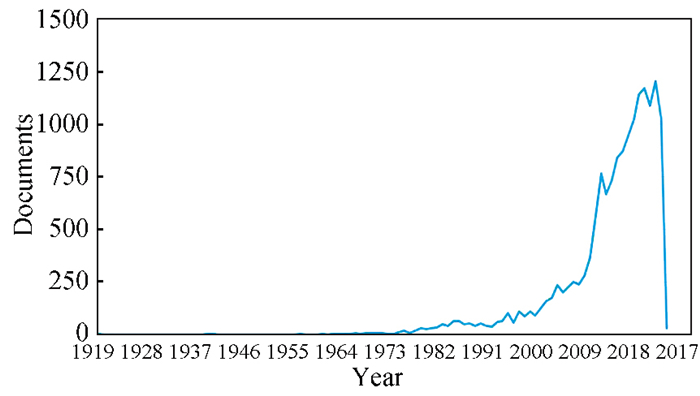
|
Fig.2 Bibliometric analysis of effect of temperature on solar cell |
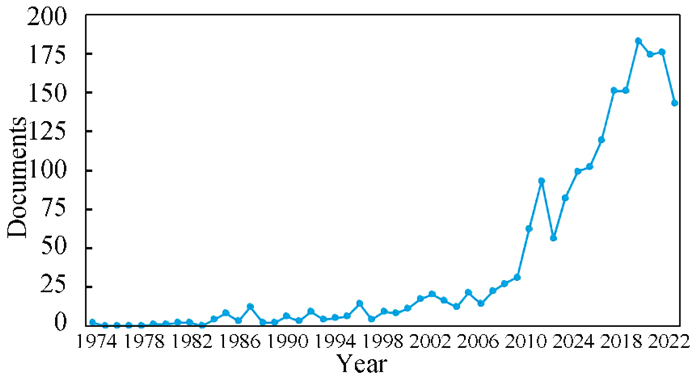
|
Fig.3 Bibliometric analysis of effect of irradiance on solar cell |
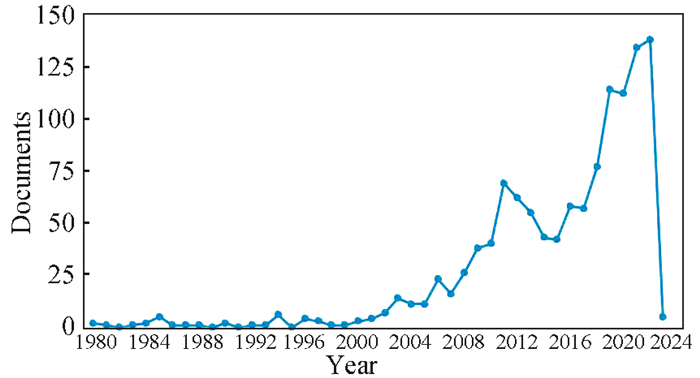
|
Fig.4 Bibliometric analysis of effect of design on solar cell |
2.1 Irradiance
The many different types of photovoltaic solar cells are affected by irradiance in a variety of ways. In PV/TE systems, the photovoltaic cells' performance is immediately as well as directly impacted by the amount of irradiation. The rise in irradiance causes the system to produce a greater amount of maximum power overall as a result of the rise. Because of this, they can only be used in areas with concentrated light Green[26]. Typical test conditions include an air mass of 1.5, a temperature of 25 ℃ and an irradiance of 1000 W/m2. Many methods may be used to determine the open circuit voltage Voc, the maximum power Pmax at different temperatures and irradiances, and the short circuit current Isc[27]. The performance of the solar panels or cells is indicated under these scenarios. These models show the interdependence between these three quantities. The commonly utilized model for open-circuit voltage as well as short-circuit current is as follows:
| $I_{\mathrm{sc}}=\frac{G}{1000}\left(I_{\mathrm{sc}, \mathrm{STC}}+\beta_{\mathrm{Isc}}(T-25)\right)$ | (1) |
where G represents the amount of light that strikes the solar cell; Isc, STC is the short circuit current produced under typical test circumstances; βIsc is the temperature coefficient for short circuit current.
| $V_{\mathrm{oc}}=V_{\mathrm{oc}, \mathrm{STC}}+\beta_{\mathrm{voc}}(T-25)+\frac{n k T}{q} \ln \left(\frac{G}{1000}\right)$ | (2) |
where Voc, STC represents the open circuit voltage produced under typical test circumstances; βvoc is the temperature coefficient of an open circuit voltage; n is the diode's ideality ratio; k is the electric charge, q is the Boltzmann constants.
The highest power is determined as:
| $P_{\max }=\frac{G}{1000}\left(P_{\max , \mathrm{STC}}+\beta_{\mathrm{pmax} }(T-25)\right)$ | (3) |
where Pmax, STC represents maximum power produced under typical test circumstances; βpmax is the heating coefficient of maximum power. Utilizing the relation, the concentrated light's maximum power can be determined.Pmax=Imax × Vmax, Imax is the maximum current and Vmax is maximum voltage.
One of the elements in Table 2 that shows the effectiveness of photovoltaic cells is the fact that silicon crystalline photovoltaic panels are most commonly utilized in terrestrial industrial and commercial settings with non-concentrated light. The same set of circumstances that were applied to all of the experiments were utilized to collect the data for these parameters. When compared with amorphous silicon PV, monocrystalline silicon PV requires approximately 2.5 times less space to create the same amount of power as amorphous silicon PV does.
| Table 2 Solar cell efficiency[36] |
Table 2 demonstrates the representative photovoltaic cells' performance for each generation utilising the critical performance indicators of open circuit voltage, short circuit current, maximum power, and efficiency measured in an accreditation body under typical test conditions of 1000 W/m2 irradiance, 25℃ temperature, and air mass 1.5. This implies that in order to opt the components that are best suited for each type of system, it is substantial to construct a competent photovoltaic system.
When there is a restriction placed on the amount of space that is available, it is essential to select the most appropriate solution. The theoretical efficiency of photovoltaic cells is affected by the number of junctions present in the cells. The efficiency of multi-junction photovoltaic cells elevates in response to focused light, with 6-junctions based on AlGaAs, GaAs, and AlGaInP paired with metamorphic Inga as exhibiting the highest efficiency of almost 50%[37]. The greatest theoretical efficiency of a solar cell with a single junction is 33.3% at 300 K and a bandgap energy of 1.14 eV, whereas the efficiency of tandem photovoltaic cells is 66%[37]. It is possible for the theoretical efficiency to be higher than 87% if the number of sub cells approaches infinity. Additionally, a single-junction solar cell's prospective efficiency can be boosted to 48.8% if the cell is cooled, and it can be enhanced to above 40% if the cell is exposed to intense light[37]. The photovoltaic (PV) systems that are based on this construction can be utilized successfully in normal irradiance; however, their effectiveness can be improved if they are utilized under concentrated light.
2.2 TemperatureThe maximum amount of electricity that solar cells can generate and their operating efficiency both get substantially impacted by the temperature.
| $P_{\max }=\beta_{\mathrm{voc}}+\beta_{\mathrm{Isc}}+\beta_{\mathrm{FF}}$ | (4) |
According to the Eq.(4), the maximum power temperature coefficient gets impacted by fill factor, short circuit current, along with open circuit voltage. Fig. 5 shows the relationship between the maximum power output and temperature for the three types of solar cells that shows the superior temperature stability of the InGaP/InGaAs/Ge cell. Multijunction solar cell is the least sensitive solar cell of the three types of photovoltaic cells to changes in temperature, as shown by the comparison between the three cells' respective decreases in maximum power as a temperature function. Several investigations have looked into how temperature affects the properties of multijunction photovoltaic cells under intense illumination[39].
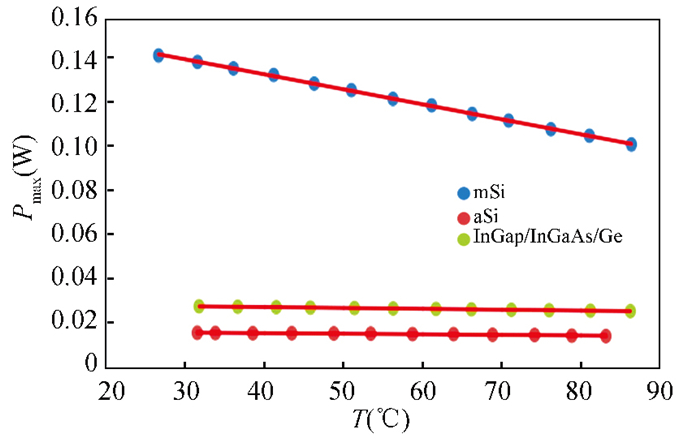
|
Fig.5 Pmax vs temperature curve[38] |
3 Geometric Design
The functionality of each individual component of PV cells is impacted by both their structure and their geometrical form[40-42]. The performance progression over time for the photovoltaic cells is considerably different, and it is depicted in Fig. 6. The most traditional form of solar cells are monocrystalline ones. The first monocrystalline photovoltaic cell was createdby Ohl in 1941[44], which marked the beginning of their development. For attaining a higher level of productivity from the solar cells, their basic design had been subjected to a number of innovations. The structure consisted of the front and bottom contacts as well as p-n junction; it was fairly straightforward. The form of the front contact was one aspect that contributed to the low efficiency, which was close to 1%. The efficiency of solar cells made of perovskite and quantum dots has increased at the fastest rate, although there are still some concerns regarding the cells' ability to remain stable. Perovskite photovoltaics utilize the tandem approach to promote stability, and during the past four years, this type's efficiency has increased by more than 20%. An anti-reflective coating, a vacuum distillation layer, a p-n junction, a back surface field, Ag front contacts along with Al bottom contacts make up this structure.
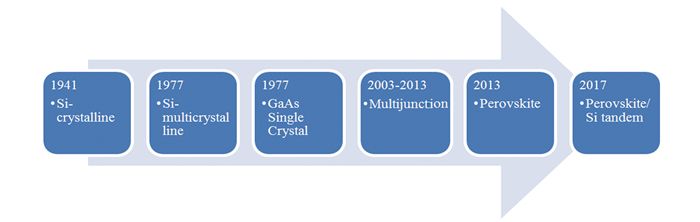
|
Fig.6 Evolution of photovoltaic cells[43] |
Several performance factors distinguish perovskite solar cells from typical semiconductor solar cells, and these differences may be examined using theoretical models[25]. Here are some observations on their disparate performance characteristics:
1) Efficiency: Perovskite solar cells have made significant progress in terms of efficiency, with record levels above 25%. They have the potential to outperform conventional solar cells' theoretical efficiency limit based on the Shockley-Queisser limit. Conventional semiconductor solar cells, such as silicon-based cells, on the other hand, have a well-established technical foundation and can dependably attain efficiencies exceeding 20%.
2) Bandgap tunability: Because perovskite materials have a wide bandgap tunability, they can absorb a wider range of the solar spectrum. This property qualifies them for tandem solar cells, in which several layers of various bandgap materials may be stacked together to improve total efficiency. The spectral absorption range of conventional semiconductor materials is limited by their relatively constant bandgaps.
3) Carrier transport: Conventional semiconductor materials have a long-established understanding of charge transport processes, which assists in the design of efficient charge collecting structures. Due to the existence of defects and ion migration, perovskite solar cells have more complicated carrier dynamics. Simulations can assist in elucidating these transport pathways and guiding the development of efficient loss-mitigation solutions.
4) Stability is a critical difficulty in perovskite solar cell development, particularly in the presence of moisture, oxygen, and light. Traditional semiconductor solar cells, such as crystalline silicon cells[45], have demonstrated long-term stability and endurance. Theoretical simulations can help designers create more stable designs by providing insights into the degradation mechanisms of perovskite materials.
5) Cost of manufacture: Conventional semiconductor solar cells benefit from a mature and well-established production infrastructure, which has helped to reduce costs over time. Because perovskite solar cells are a relatively new technology, scaling up production and lowering manufacturing costs remain hurdles. Theoretical simulations may aid in the optimization of manufacturing processes as well as the identification of cost-effective materials and device layouts.
Inclusive, theoretical simulations are critical for understanding the underlying physics and performance constraints of both perovskite and conventional semiconductor solar cells. They give essential insights that direct the development of innovative materials, device designs, and manufacturing procedures, resulting in better solar cell performance.
There are a few different architectures that can be utilised for silicon photovoltaic cells when working with concentrated light. The CMOS semiconductor technology was utilised to acquire this particular cell. When exposed to focused light, multijunction photovoltaic cells perform the best. Triple junction photovoltaic cell is made up of the following components: contacts, a buffer layer, three junctions made of GaAs, InGaAs, and InGaP two tunel junctions (TJ) whose purpose is to decrease the series resistance and parasitic absorption, and a buffer layer also these cells are the ones that are utilised the most. The optimizations of the sizes need to result in a decrease in the series resistance as well as a maximisation of the solar cell's front active area to attain success. Sadly, these dimensions are affected by the concentration rate in some way. The optimal size must be determined by finding a balance that's satisfactory across all three of these factors. Although the producers of commercial silicon photovoltaic cells attempted to make by utilizing various technologies, optimizing the dimension, and lowering the cost, the cells ideal for concentrated light. Despite the fact that multijunction cells are expensive, the current tendency is to use them. This is due to the efficiency of the multijunction cells, that can be improved even further and now exceeds 50% when compared to silicon photovoltaic cells, yielding very good reliability Green[36].
4 Parameter Optimization of Solar Cells Using Meta-Heuristic AlgorithmsThe study focuses on the development of metaheuristic algorithms that are influenced by biological processes. We separated the bio-inspired algorithms that were utilized in the solar cell discovery characteristics into three primary categories: swarm intelligence-based algorithms, evolutionary algorithms, and ecological-relationship-based algorithms.Difference algorithms are employed for the same purpose. Some of them are illustrated in Table 3. In light of the fact that practically all metaheuristic algorithms are plagued by premature convergence, it is important to point out that some researchers have merged or hybridised various algorithms in order to circumvent the inadequacies that they present.
Every single metaheuristic algorithm goes through a cycle of phases that are very similar to one another but differ in their specifics. In the meantime, the main application of stochasticity occurs during the process of initialising the first population. This can be accomplished by either selecting randomly among potential solutions that are contained within predetermined bounds or by employing a mathematical procedure that produces randomly selected potential solutions that are contained within predetermined bounds (i.e., upper and lower limits). Fig. 7 provides a high-level overview of bio-inspired metaheuristic algorithms, and Table 3 defined some of the common approaches based on meta-heuristic optimization algorithm.
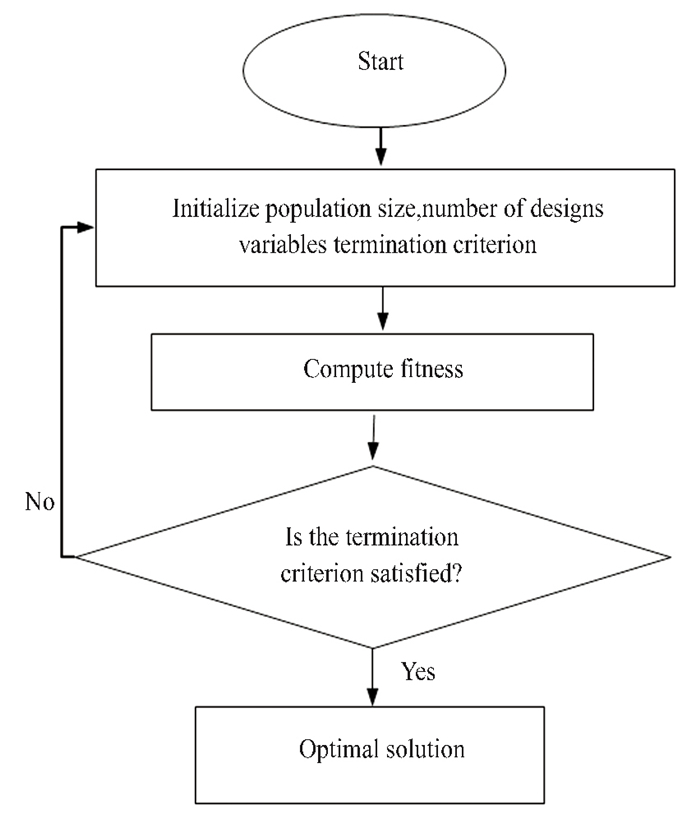
|
Fig.7 Generic flowchart of optimization algorithms |
In the first stage, the population (or the next-generation population) is initialised in one of three ways: through the random choosing the design variables (and hence the potential solutions), while adhering to the predetermined limitations, using a mathematical formula or approach, or through the update function of an algorithm in the event of a subsequent iteration. This phase demonstrates how the objective function has been utilised for computing the optimal solutions in the solution space, and how they are ranked either ascendingly or descendingly based on the results of the calculation. In addition, the algorithm also explores its environment.
This stage demonstrates how effectively the algorithm uses its resources. Potential candidate solutions are generated in the second step by the update function or algorithm mechanism, which considers the previously generated solutions, random parameters within a known range (often [0, 1]), as well as control parameters which are unavailable in all metaheuristic approaches. The modified candidate solutions' fitness values are also computed once more, and based on how they compare, they are ranked higher or lower.
In the third phase, depending on the situation, the candidate solutions with the highest fitness values are identified and ranked in either ascending or descending order. In this stage of the process, the elements being compared are those from the initial population and those from the updated elements. After then, the criteria for quitting are investigated. Therefore, the iteration or the generation comes to a conclusion with this step. In the following Table 3, GO stands for Genetic Algorithm, GWO for Grey Wolf Optimization, PSO for Particle Swarm Optimization, and WOA for Whale Optimization Algorithm.
5 Current Limitations and Future Research DirectionsIn photovoltaics, the fundamental problems may be related to sub-bandgap photon energy loss and above-bandgap thermalization loss, both of which reduce the device performance. Thermionic emission is an intriguing alternative to photovoltaics that has the potential to transform this difficulty into an advantage. Despite the fact that thermionic energy converters (TECs) with metallic electrodes were formerly explored for the conversion of solar energy, photovoltaics won out in the end due to the numerous other hurdles. The utilisation of various materials for photovoltaics is a more recent advancement in solar thermionics that has occurred (i.e., semiconductors). There are, however, certain fundamental issues that have yet to be resolved, such as whether or not a semiconductor would function in thermionic emission and what the trends in solar cell behaviour and performance of semiconductor parameters are. Semiconductor materials are an essential component of solar cells, despite the many other parts that make up these cells. The challenge of selecting the material with the appropriate qualities from among the vast array of materials that are available is a laborious one. For the development of a complete solar cell, it is substantial to have a thorough comprehension of the functional requirements of each component as well as an examination of a variety of key elements. It is a challenging task to consider all of the attributes at the same time when selecting materials; as a result, it is necessary to take a methodical approach to the process of selecting materials in order to screen and choose the best material for the device application. Even though there is an abundance of semiconducting materials on the market, not all of them are suitable for use in solar applications. In order to advance business interests, it is necessary to find solutions to a number of environmental challenges[18-19]. Fig. 8 provides visual representations of a few of these contributing components.
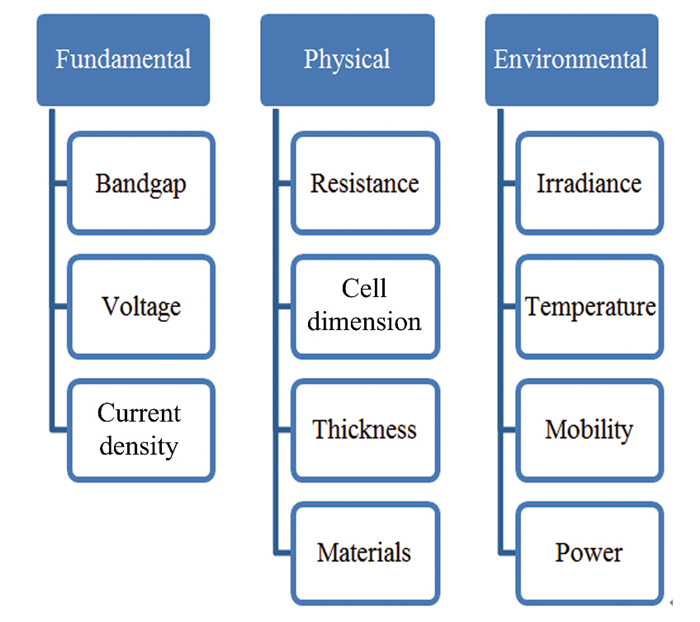
|
Fig.8 Semiconductors for solar cell application's parameters |
For the parameters, here are some potential future study directions:
1) Bandgap: Future research might focus on developing new materials with changeable bandgaps to allow for more efficient utilization of a larger range of the solar spectrum. Exploration of perovskite alloys, quantum dots, and other new materials may lead to tunable bandgaps and enhanced light harvesting.
2) Voltage: Researchers might look at novel device designs and material combinations to improve the voltage output of solar cells. This may entail investigating tandem or multi-junction solar cells in order to reach greater voltages and more efficient utilization of the solar spectrum.
3) Current density: Future research may focus on increasing current density by advances in charge carrier conveyance and collecting. Investigating new charge transport materials, interface engineering approaches, and optimising device architectures can all assist to reduce recombination losses and increase current density.
Physical characteristics:
1) Resistance: Future research might concentrate on lowering both series and shunt resistances in solar cells. This may entail the development of enhanced contact materials and interfaces, the optimisation of charge extraction layers, and the investigation of novel approaches for enhancing the conductivity of transparent conductive electrodes.
2) Cell dimension: Research might look at the best cell dimensions for various types of solar cells in order to maximise light absorption and charge carrier collection. Investigating novel light-trapping structures, nanostructured architectures, and enhanced optical design can result in increased efficiency via optimised cell dimensions.
3) Thickness: Future study may look at the effect of thickness changes on solar cell performance. This might entail researching the effects of ultra-thin absorber layers and creating ways for effective charge extraction from thin films while retaining high optical absorption.
4) Materials: Research might concentrate on creating novel materials with higher stability, charge transport qualities, and low-cost production processes. Exploring materials other than silicon, such as perovskites, organic semiconductors, and 2D materials, might open up new possibilities for efficient and scalable solar cell technology.
Environmental Parameters:
1) Irradiance: Future research might concentrate on the development of improved light management systems to improve light absorption and utilisation. Exploring improved nanostructured materials, plasmonic structures, and light concentration methods to increase solar cell performance under variable irradiance circumstances might be part of this.
2) Temperature: Research might look at how temperature affects solar cell efficiency and techniques for mitigating temperature-related losses. Developing innovative thermal management systems, materials with greater temperature stability, and optimising device designs for high-temperature situations might all be part of this.
3) Mobility: Future research might focus on increasing charge carrier mobility in semiconducting materials utilised in solar cells. This might include designing materials to improve charge transport qualities, experimenting with new charge transport materials, and studying the effect of flaws and interfaces on carrier mobility.
4) Power: The research might concentrate on increasing power production and total energy conversion efficiency. This might entail investigating sophisticated device topologies such as multi-junction or tandem cells, as well as optimising energy harvesting from different sun spectrum areas using spectral splitting techniques.
These future research initiatives aim to solve present limits, improve solar cell performance, and pave the way for more efficient, cost-effective, and environmentally friendly solar energy conversion technologies.
6 ConclusionsOne of the most labor-intensive as well as resource-intensive forms of renewable electricity generation is solar power generation. It has several advantages that distinguish it different from other forms of energy, such as fossil fuels as well as petroleum resources. It is an alternative that has the potential to be successful and is reliable in meeting the growing demand for energy. Even if the processes for harnessing solar energy are straightforward, an effective and long-lasting solar material is still required. A semiconductors-based solar cell technology has the potential to convert more than sixty percent of the total sun spectrum into electric power. This sector has a number of obstacles, the most significant of which is the need to reduce the overall cost of production, increase public awareness, and improve infrastructure. In this particular piece of research, a variety of semiconductors are examined, and the environmental factors that influence them, such as irradiance, temperature, and others, are investigated. In this research, we developed some met heuristic optimization techniques for the purpose of enhancing the solar cells' performance. Therefore, solar energy is the solution to today's energy problems, and research on solar cells has a bright future across the globe.
| [1] |
Xiao Z, Yuan Y, Wang Q, et al. Thin-film semiconductor perspective of organometal trihalide perovskite materials for high-efficiency solar cells. Materials Science and Engineering: R: Reports, 2016, 101: 1-38. DOI:10.1016/j.mser.2015.12.002 (  0) 0) |
| [2] |
Feldmann F, Bivour M, Reichel C, et al. Passivated rear contacts for high-efficiency n-type Si solar cells providing high interface passivation quality and excellent transport characteristics. Solar Energy Materials & Solar Cells, 2014, 120, Part A: 270-274. DOI:10.1016/j.solmat.2013.09.017 (  0) 0) |
| [3] |
Chen W, Shi Y, Wang Y, et al. N-type conjugated polymer as efficient electron transport layer for planar inverted perovskite solar cells with power conversion efficiency of 20.86%. Nano Energy, 2020, 68: 104363. DOI:10.1016/j.nanoen.2019.104363 (  0) 0) |
| [4] |
Shi J, Wang Y, Yang M, et al. Enhanced interface properties of solution-processed antimony sulfide planar solar cells with n-type indium sulfide buffer layer. Electrochimica Acta, 2021, 376: 138031. DOI:10.1016/j.electacta.2021.138031 (  0) 0) |
| [5] |
Hysa A. Modeling and simulation of the photovoltaic cells for different values of physical and environmental parameters. Engineering Science Journal, 2019, 3(6): 395-406. (  0) 0) |
| [6] |
Burgelman M, Nollet P, Degrave S. Modelling polycrystalline semiconductor solar cells. Thin Solid Films, 2000, 361-362: 527-532. DOI:10.1016/S0040-6090(99)00825-1 (  0) 0) |
| [7] |
Ouédraogo A, Zouma B, Ouédraogo E, et al. Individual efficiencies of a polycrystalline silicon PV cell versus temperature. Results in Optics, 2021, 4: 100101. DOI:10.1016/j.rio.2021.100101 (  0) 0) |
| [8] |
Chavali R, Jian V, Li C, et al. A generalized theory explains the anomalous suns Voc response of Si heterojunction solar cells. IEEE Journal of Photovoltaics, 2017, 7(1): 169-176. DOI:10.1109/JPHOTOV.2016.2621346 (  0) 0) |
| [9] |
Brammertz G, Oueslati S, Buffiere M, et al. , Investigation of properties limiting efficiency in Cu2ZnSnSe4-based solar cells. IEEE Journal of Photovoltaics, 2015, 5(2): 649-655. DOI:10.1109/JPHOTOV.2014.2376053 (  0) 0) |
| [10] |
Paretkar D, Glassmaker N J, Mikeska K R, et al. Adhesion of screen-printed silver metallization to crystalline silicon solar cells. IEEE Journal of Photovoltaics, 2016, 6(5): 1141-1151. DOI:10.1109/JPHOTOV.2016.2583792 (  0) 0) |
| [11] |
Berney Needleman D, Mailoa J P, Brandt R E, et al. Sensitivity analysis of optical metrics for spectral splitting photovoltaic systems: A case study. IEEE Journal of Photovoltaics, 2015, 5(5): 1380-1388. DOI:10.1109/JPHOTOV.2015.2457292 (  0) 0) |
| [12] |
Asim M, Mallick M A, Malik A, et al. Modelling and simulation of 5 parameter model of solar cell. International Journal of Electronics, Electrical and Computational System, 2015, 4(Special Issue): 38-42. (  0) 0) |
| [13] |
Sarkar M N I. Effect of various model parameters on solar photovoltaic cell simulation: A SPICE analysis. Renewables Wind, Water, and Solar, 2016, 3: Article number: 13. DOI:10.1186/s40807-016-0035-3 (  0) 0) |
| [14] |
Alonso-Álvarez D, Wilson T, Pearce P, et al. Solcore: a multi-scale, Python-based library for modelling solar cells and semiconductor materials. Journal of Computational Electronics, 2018, 17(3): 1099-1123. DOI:10.1007/s10825-018-1171-3 (  0) 0) |
| [15] |
Kuhlmann B, Aberle A G, Hezel R, et al. Simulation and optimization of metal-insulator-semiconductor inversion-layer silicon solar cells. IEEE Transactions on Electron Devices, 2000, 47(11): 2167-2178. DOI:10.1109/16.877180 (  0) 0) |
| [16] |
Song J, Li S S, Huang C H, et al. Device modeling and simulation of the performance of Cu(In1-x, Gax)Se2 solar cells. Solid-State Electronics, 2004, 48(1): 73-79. DOI:10.1016/S0038-1101(03)00289-2 (  0) 0) |
| [17] |
Fell A, McIntosh K R, Fong F C. Simplified device simulation of silicon solar cells using a lumped parameter optical model. IEEE Journal of Photovoltaics, 2016, 6(3): 611-616. DOI:10.1109/JPHOTOV.2016.2528407 (  0) 0) |
| [18] |
Wasmer S, Fell A, Greulich J M. Influence of fundamental model uncertainties on silicon solar cell efficiency simulations. IEEE Transactions on Electron Devices, 2019, 66(1): 524-532. DOI:10.1109/TED.2018.2882776 (  0) 0) |
| [19] |
Liu Z, Sahraei N, Hoex B, et al. Optical modeling of alkaline saw-damage-etched rear surfaces of monocrystalline silicon solar cells. IEEE Journal of Photovoltaics, 2014, 4(6): 1436-1444. DOI:10.1109/JPHOTOV.2014.2349657 (  0) 0) |
| [20] |
Li M, Ma F-J, Peters L M, et al. Numerical simulation of doping process by BBr3 tube diffusion for industrial n-type silicon wafer solar cells. IEEE Journal of Photovoltaics, 2017, 7(3): 755-762. DOI:10.1109/JPHOTOV.2017.2679342 (  0) 0) |
| [21] |
Soeriyadi A H, Wang L, Conrad B, et al. Extraction of essential solar cell parameters of subcells in a tandem structure with a novel three-terminal measurement technique. IEEE Journal of Photovoltaics, 2018, 8(1): 327-332. DOI:10.1109/JPHOTOV.2017.2762596 (  0) 0) |
| [22] |
Liu X, Lian H, Zhou Z, et al. Stoichiometric dissolution of defective CsPbI2Br surfaces for inorganic solar cells with 17.5% efficiency. Advanced Energy Materials, 2022, 12(14): 2103933. DOI:10.1002/aenm.202103933 (  0) 0) |
| [23] |
Li Q, Zheng Y, Wei Z, et al. Halide diffusion equilibrium and its impact on efficiency evolution of perovskite solar cells. Advanced Energy Materials, 2022, 12(48): 2202982. DOI:10.1002/aenm.202202982 (  0) 0) |
| [24] |
PV Lighthouse. The solar cell under illumination. https://www2.pvlighthouse.com.au/resources/courses/altermatt/The%20PV%20Principle/The%20solar%20cell%20under%20illumination.aspx.
(  0) 0) |
| [25] |
Kumari N, Singh S K, Kumar S. A comparative study of different materials used for solar photovoltaics technology. Materials Today: Proceedings, 2022, 66(part 8): 3522-3528. DOI:10.1016/j.matpr.2022.06.403 (  0) 0) |
| [26] |
Green M A, Dunlop E D, Hohl-Ebinger J, et al. Solar cell efficiency tables (version 59). Progress in Photovoltaics: Research and Applications, 2022, 30(1): 3-12. DOI:10.1002/pip.3506 (  0) 0) |
| [27] |
Yoshikawa K, Kawasaki H, Yoshida W, et al. Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%. Nature Energy, 2017, 2(5): 17032. DOI:10.1038/nenergy.2017.32 (  0) 0) |
| [28] |
Hao Q, Xu H, Xiao G. Hybrid photon-enhanced thermionic emission and photovoltaic converter with concentrated solar power. Solar Energy Materials and Solar Cells, 2023, 254: 112279. DOI:10.1016/j.solmat.2023.112279 (  0) 0) |
| [29] |
Callies A, Hanser M, Goldschmidt J C, et al. Structuring of perovskite-silicon tandem solar cells for reduced reflectance and thermalization losses. Optics Express, 2023, 31(12): 19428-19442. DOI:10.1364/OE.491371 (  0) 0) |
| [30] |
Wu J L, Hirai Y, Kato T, et al. New world record efficiency up to 22.9% for Cu (In, Ga)(Se, S)2 thin-film solar cells. Proceedings of the 7th World Conference on Photovoltaic Energy Conversion (WCPEC-7), Waikoloa, 2018.
(  0) 0) |
| [31] |
First Solar INC. First solar builds the highest efficiency thin film PV cell on record. 2014.
(  0) 0) |
| [32] |
Yang W S, Noh J H, Jeon N J, et al. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science, 2015, 348(6240): 1234-1237. DOI:10.1126/science.aaa9272 (  0) 0) |
| [33] |
Takamoto T, Washio H, Juso H. Application of InGaP/GaAs/InGaAs triple junction solar cells to space use and concentrator photovoltaic. Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC). Piscataway: IEEE, 2014: 1-5.
(  0) 0) |
| [34] |
Sasaki K, Agui T, Nakaido K, et al. Development of InGaP/GaAs/InGaAs inverted triple junction concentrator solar cells. Proceedings of the 9th International Conference on Concentrating Photovoltaic Systems(CPV-9). Miyazaki, 2013: 22-25.
(  0) 0) |
| [35] |
Hosoya M, Oooka H, Nakao H, et al. Organic thin film photovoltaic modules. Proceedings of the 93rd Annual Meeting of the Chemical Society of Japan. Tokyo: The Chemical Society of Japan, 2013: 21-37.
(  0) 0) |
| [36] |
Green M, Dunlop E, Hohl-Ehinger J, et al. Solar cell efficiency tables (version 57). Progress in Photovoltaics: Research and Applications, 2022, 29(1): 3-15. DOI:10.1002/pip.3371 (  0) 0) |
| [37] |
Alharbi F H, Kais S. Theoretical limits of photovoltaics efficiency and possible improvements by intuitive approaches learned from photosynthesis and quantum coherence. Renew. Sustain. Energy Rev., 2015, 43: 1073-1089. DOI:10.48550/arXiv.1402.1923 (  0) 0) |
| [38] |
Cotfas D T, Cotfas P A, Mahmoudinezhad S, et al. Critical factors and parameters for hybrid photovoltaic-thermoelectric systems; review. Applied Thermal Engineering, 2022, 215: 118977. DOI:10.1016/j.applthermaleng.2022.118977 (  0) 0) |
| [39] |
Cotfas D T, Cotfas P A, Machidon O M. Study of temperature coefficients for parameters of photovoltaic cells. International Journal of Photoenergy, 2018, 2018: Article ID 5945602. DOI:10.1155/2018/5945602 (  0) 0) |
| [40] |
Geisz J F, Steiner M A, Jain N, et al. Building a six-junction inverted metamorphic concentrator solar cell. IEEE Journal of Photovoltaics, 2018, 8(2): 626-632. DOI:10.1109/JPHOTOV.2017.2778567 (  0) 0) |
| [41] |
Slade A, Garboushian V. 27.6% efficient silicon concentrator cell for mass production. Technical Digest, In Proceedings of the 15th International Photovoltaic Science and Engineering Conference. Shanghai, 2005.701.
(  0) 0) |
| [42] |
Sharp Corporation sharp develops concentrator solar cell with world's highest conversion efficiency of 43.5% http://global.sharp/corporate/news/120531.html(2021-09-14).
(  0) 0) |
| [43] |
NREL Transforming ENERGY. Photovoltaic research. https://www.nrel.gov/pv/cell-efficiency.html (Accessed on 29.11.2022)
(  0) 0) |
| [44] |
Ohl R S. Light-Sensitive Electric Device. U. S. Patent 2402662 (Filed May 27, 1941, Issued June 25, 1946).
(  0) 0) |
| [45] |
Meier J, Spitznagel J, Kroll U, et al. Potential of amorphous and microcrystalline silicon solar cells. Thin Solid Films, 2004, 451-452: 518-524. DOI:10.1016/j.tsf.2003.11.014 (  0) 0) |
| [46] |
Askarzadeh A, dos Santos Coelho L. Determination of photovoltaic modules parameters at different operating conditions using a novel bird mating optimizer approach. Energy Conversion and Management, 2015, 89: 608-614. DOI:10.1016/j.enconman.2014.10.025 (  0) 0) |
| [47] |
Benkercha R, Moulahoum S, Colak I, et al. PV module parameters extraction with maximum power point estimation based on flower pollination algorithm. Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC). Piscatway: IEEE, 2016: 442-449. DOI: 10.1109/EPEPEMC.2016.7752038.
(  0) 0) |
| [48] |
Cheng M-Y, Prayogo D. Symbiotic organisms search: A new metaheuristic optimization algorithm. Computers & Structures, 2014, 139: 98-112. DOI:10.1016/j.compstruc.2014.03.007 (  0) 0) |
| [49] |
Chin V J, Salam Z. Coyote optimization algorithm for the parameter extraction of photovoltaic cells. Solar Energy, 2019, 194: 656-670. DOI:10.1016/j.solener.2019.10.093 (  0) 0) |
| [50] |
Deotti L M P, Pereira J L R, da Silva Júnior I C. Parameter extraction of photovoltaic models using an enhanced Lévy flight bat algorithm. Energy Conversion and Management, 2018, 221: 113114. DOI:10.1016/j.enconman.2020.113114 (  0) 0) |
| [51] |
El-Fergany A A. Parameters identification of PV model using improved slime mould optimizer and Lambert W-function. Energy Reports, 2021, 7: 875-887. DOI:10.1016/j.egyr.2021.01.093 (  0) 0) |
| [52] |
Fathy A, Rezk H. Robust electrical parameter extraction methodology based on Interior Search Optimization Algorithm applied to supercapacitor. ISA Transactions, 2020, 105: 86-97. DOI:10.1016/j.isatra.2020.05.016 (  0) 0) |
| [53] |
Guo L, Meng Z, Sun Y, et al. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Conversion and Management, 2016, 108: 520-528. DOI:10.1016/j.enconman.2015.11.041 (  0) 0) |
| [54] |
Heidari A A, Mirjalili S, Faris H, et al. Harris hawks optimization: Algorithm and applications. Future Generation Computer Systems, 2019, 97: 849-872. DOI:10.1016/j.future.2019.02.028 (  0) 0) |
| [55] |
Li S, Gong W, Gu Q. A comprehensive survey on meta-heuristic algorithms for parameter extraction of photovoltaic models. Renewable and Sustainable Energy Reviews, 2021, 141(Issue C): 110828. DOI:10.1016/j.rser.2021.110828 (  0) 0) |
| [56] |
Louzazni M, Khouya A, Amechnoue K, et al. Parameter estimation of photovoltaic module using bio-inspired firefly algorithm. Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC). 2016: 591-596. DOI: 10.1109/IRSEC.2016.7983895.
(  0) 0) |
| [57] |
Merchaoui M, Sakly A, Mimouni M F. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Conversion and Management, 2018, 175: 151-163. DOI:10.1016/j.enconman.2018.08.081 (  0) 0) |
| [58] |
Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Systems, 2015, 89: 228-249. DOI:10.1016/j.knosys.2015.07.006 (  0) 0) |
| [59] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 (  0) 0) |
| [60] |
Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 (  0) 0) |
| [61] |
Mokeddem D. Parameter extraction of solar photovoltaic models using enhanced levy flight based grasshopper optimization aAlgorithm. Journal of Electrical Engineering & Technology, 2016, 16(1): 171-179. DOI:10.1007/s42835-020-00589-1 (  0) 0) |
| [62] |
Nayak B, Mohapatra A, Mohanty K B. Parameter estimation of single diode PV module based on GWO algorithm. Renewable Energy Focus, 2019, 30: 1-12. DOI:10.1016/j.ref.2019.04.003 (  0) 0) |
| [63] |
Oliva D, Abd El Aziz M, Ella Hassanien A. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Applied Energy, 2019, 200: 141-154. DOI:10.1016/j.apenergy.2017.05.029 (  0) 0) |
| [64] |
Ridha H M, Heidari A A, Wang M, et al. Boosted mutation-based Harris hawks optimizer for parameters identification of single-diode solar cell models. Energy Conversion and Management, 2020, 209: 112660. DOI:10.1016/j.enconman.2020.112660 (  0) 0) |
| [65] |
Saremi S, Mirjalili S, Lewis A. Grasshopper optimisation algorithm: Theory and application. Advances in Engineering Software, 2017, 105: 30-47. DOI:10.1016/j.advengsoft.2017.01.004 (  0) 0) |
| [66] |
Song Y, Wu D, Wagdy Mohamed A, et al. Enhanced success history adaptive de for parameter optimization of photovoltaic models. Complexity, 2021, 2021: 1-22. DOI:10.1155/2021/6660115 (  0) 0) |
| [67] |
Subudhi B, Pradhan R. Bacterial foraging optimization approach to parameter extraction of a photovoltaic module. IEEE Transactions on Sustainable Energy, 2018, 9(1): 381-389. DOI:10.1109/TSTE.2017.2736060 (  0) 0) |
| [68] |
Xiong G, Zhang J, Shi D, et al. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Conversion and Management, 2018, 174: 388-405. DOI:10.1016/j.enconman.2018.08.053 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


