2. Information Materials and Intelligent Sensing Laboratory of Anhui Province, Anhui University, Hefei 230601, China;
3. School of Artificial Intelligence, Anhui University, Hefei 230601, China;
4. Intelligent Interconnected Systems Laboratory of Anhui Province (Hefei University of Technology), Hefei 230009, China;
5. School of Software, Hefei University of Technology, Hefei 230009, China
Polarimetric synthetic aperture radar (PolSAR) is a radar system with all-weather, all-day capability, and it can provide more polarization information than traditional single-polarization SAR systems, including target scattering matrices and polarization scattering characteristics[1-3]. This information can be used for terrain classification[4], change detection[5], target recognition[6], and so on. Among them, PolSAR terrain classification plays an important role in understanding and interpreting remote sensing images, and it has become a research hot-topic[7-9].
PolSAR terrain classification mainly contains two steps: feature extraction and classification. In general, polarization decomposition stands as a highly effective and extensively utilized technique for extracting features from PolSAR images, it can effectively extract the scattering information embedded in the full polarization scattering matrix. Traditional polarization decomposition encompasses several established methods, including Pauli decomposition[10], Freeman-Durden decomposition[11], Cloude-Pottier decomposition[12], Touzi decomposition[13], H/α decomposition[14], Krogager decomposition[15], and so on[16-17]. Apart from the extracted polarimetric features, statistical features, color features, texture features[18-20], as well as other popular features, have also been used for terrain classification.
Then, the extracted features are fed into a classification network to obtain the final terrain classification results. Typically, there are two types of classification networks: unsupervised classification and supervised classification, depending on whether labeled data is required. The unsupervised classification methods, such as mean shift[21], fuzzy clustering[22], k-means clustering[23], can achieve terrain classification by automatically identifying the patterns and groups within unlabeled training data, which means these methods can learn the intrinsic properties of the data without relying on labeled data for training. Besides, there are two types of supervised classification methods: traditional machine learning methods and deep learning methods, based on the differences in model structure[24]. Traditional machine learning methods mainly include Naive Bayes[25], decision trees[26], support vector machine (SVM)[27] and Adaptive Boosting (AdaBoost)[28]. Nevertheless, the performance of traditional machine learning methods heavily relies on the quality of feature representation. When the extracted features fail to effectively capture the differences between different terrain categories, the classification performance drops significantly. Additionally, these methods often have poor generalization performance, which may lead to overfitting or underfitting.
Over the past few years, with the continuous development of deep learning technology, many researchers have started to use convolutional neural networks (CNN) for PolSAR terrain classification[29]. Compared with the traditional machine learning methods, CNN can automatically learn to extract features from PolSAR images through backpropagation, without the need for manual feature design. Additionally, PolSAR data contains a large amount of high-dimensional polarization information, which makes it difficult for traditional machine learning methods to handle, while CNN can effectively process high-dimensional data. Zhou et al.[30] first applied CNN to PolSAR terrain classification. They proposed a CNN structure consisting of two convolutional layers, two max-pooling layers, and two fully connected layers, and achieved ideal results in PolSAR terrain classification. Hua et al.[31] proposed a dual-channel CNN (Dc-CNN) for PolSAR terrain classification. Dc-CNN consists of two parallel CNNs that can extract and fuse the features of different scales, thereby improving the accuracy of terrain classification. Liu et al.[32] proposed a polarized convolutional network (PCN), which fully utilizes the polarization information contained in PolSAR images. Moreover, they proposed a polarization scattering coding method for processing the polarization scattering matrix and obtaining a nearly complete feature. The polarization scattering coding method can also completely preserve the polarization information of the scattering matrix. Based on the polarization scattering coding and convolutional neural network, PCN greatly improves the performance of PolSAR terrain classification. Polarimetric squeeze-and-excitation network (PSE-Net)[33] introduces the squeeze-and-excitation operation into CNN to effectively combine the polarimetric and spatial features, thus generating more discriminative feature representations. Zhang et al.[34] proposed a complex-valued CNN (CV-CNN) for PolSAR terrain classification. In this method, all the elements of CNN are extended to the complex domain, and a complex backpropagation algorithm is developed for CV-CNN training. This method shows great potential for PolSAR image analysis due to its ability to handle complex-valued data. In addition, as milestone innovations in the development of convolutional neural networks, VGG-Net[35] and ResNet[36] have also been used for PolSAR terrain classification. VGG-Net designs a structure of deep stacked convolutional layers and pooling layers to learn richer deep features. ResNet uses residual blocks to construct the network, and each residual block contains a skip connection, which allows ResNet to have a deep network structure.
These state-of-the-art algorithms have shown significant improvements and achieved high classification accuracy in PolSAR terrain classification. They possess powerful deep feature extraction capabilities, enabling effective extraction of global deep features from PolSAR images, capturing the characteristics of different terrains. However, these algorithms usually have deep network structures, which means that they require more training samples and time to achieve optimal training performance. In addition, these algorithms overlook local edge and shape features during the processing, resulting in an incomplete representation of PolSAR terrain features and impacting the accuracy of terrain classification[37]. In fact, edge and shape features play a crucial role in PolSAR terrain classification. Edge features provide information about the contours of land objects, aiding in the differentiation of boundaries between different land types. Shape features, on the other hand, offer geometric properties of land objects, facilitating the further distinction of similar types of land. Neglecting these local features can lead to missing or confusing terrain classification results.
Therefore, to address the above-mentioned issues, this article proposes a method that combines deep learning algorithms with local edge detection methods: HOG-VGG. HOG-VGG combines two different feature extraction methods, VGG network and HOG descriptor[38]. HOG can extract local edge information by computing the distribution of gradient orientations within image blocks, making it particularly suitable for detecting and representing object boundaries and shape contours. VGG network focuses on extracting global deep features from images. By adopting a deep convolutional neural network structure, VGG learns hierarchical representations that can capture high-level concepts and semantic information. These global features provide a broader context and understanding of the entire image. HOG-VGG combines the strengths of HOG and VGG, fully leveraging their complementarity. HOG emphasizes local edge details, while VGG complements it by capturing overall and high-level information. By fusing local and global features, HOG-VGG enhances the feature representation completeness and exhibits high classification accuracy.
The main contributions of the proposed HOG-VGG are as follows.
1) HOG-VGG combines the strengths of two different feature extraction methods, namely VGG network and HOG descriptor, to achieve effective multi-level feature fusion. Specifically, HOG extracts local edge features while VGG extracts global deep features. Thus HOG-VGG solves the problem that VGG ignores the local edge features and enhances the feature representation completeness.
2) HOG-VGG specially designs a feature fusion strategy to optimally fuse the global deep features and local edge features. And the optimal weight coefficients for feature fusion are obtained during network training by minimizing the loss function.
3) The proposed HOG-VGG is experimented on two real PolSAR datasets, and our method achieves the best classification performance among all methods. This result indicates that HOG-VGG is an effective PolSAR terrain classification method.
The rest of this article is organized as follows: Section 1 presents a comprehensive explanation of the HOG-VGG algorithm. Section 2 analyzes the classification results of different methods on two PolSAR datasets. Finally, Section 3 provides a summary of this article.
1 MethodologyThe framework of the proposed HOG-VGG is shown in Fig. 1. As shown in the figure, HOG-VGG mainly consists of several key modules, including PolSAR image preprocessing block, global deep feature extraction block based on VGG, local edge feature extraction block based on HOG, feature fusion block, and the final classification block.
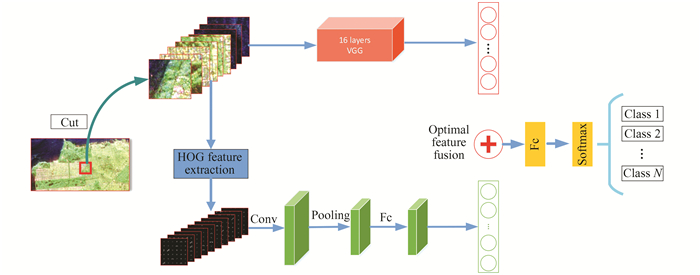
|
Fig.1 Overall framework of HOG-VGG |
Firstly, PolSAR images are processed by polarization decomposition, and the polarization decomposition technology used in this article is Pauli decomposition. The decomposed features can adequately represent the scattering information of different categories contained in the full polarization scattering matrix, thus laying a foundation for subsequent classification. The feature map after Pauli decomposition is cut into image slices of the same size as the input data of the feature extraction network. Next, the VGG network extracts global deep features while HOG extracts local edge features. After that, these two types of features are optimally fused, and the fused features are input into the final classification module to complete the classification task. The following parts will provide a detailed description of the proposed HOG-VGG.
1.1 Preprocessing of PolSAR ImageIn PolSAR images, the scattering characteristics of each resolution cell can be described as follows:
| $ \boldsymbol{S}=\left[\begin{array}{ll} S_{\mathrm{HH}} & S_{\mathrm{HV}} \\ S_{\mathrm{VH}} & S_{\mathrm{VV}} \end{array}\right] $ |
where SHH, SHV, SVH and SVV represent scattering coefficients, HH and VV represent co-polarization, while HV and VH represent cross-polarization. Based on the Pauli decomposition and reciprocity principle, S can be simplified into a vector K, which can be defined as
| $ \boldsymbol{K}=\frac{1}{\sqrt{2}}\left[S_{\mathrm{HH}}+S_{\mathrm{VV}}, S_{\mathrm{HH}}-S_{\mathrm{VV}}, 2 S_{\mathrm{HV}}\right]^{\mathrm{T}} $ |
Then, the coherence matrix is calculated as follows:
| $ \boldsymbol{T}=\boldsymbol{K} \cdot \boldsymbol{K}^{\mathbf{H}}\left[\begin{array}{lll} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{array}\right] $ |
Next, the coherence matrix T is transformed into a 6-D feature vector to conform to the input format of the subsequent neural network. The transformation method can be described as follows:
| $ \begin{gathered} A=10 \log _{10}(\text { Span }) \\ B=T_{22} / \text { Span } \\ C=T_{33} / \text { Span } \\ D=\left|T_{12}\right| / \sqrt{T_{11} \cdot T_{22}} \\ E=\left|T_{13}\right| / \sqrt{T_{11} \cdot T_{33}} \\ F=\left|T_{23}\right| / \sqrt{T_{33} \cdot T_{22}} \end{gathered} $ |
where A represents the decibel value of the total scattered power, and Span=T11+T22+T33. B and C represent the normalized power ratios of T22 and T33, respectively. D, E and F represent the relative correlation coefficients.
1.2 Deep Feature Extraction Based on VGGVGG is a highly influential convolutional neural network architecture in the field of computer vision, and its name comes from the Visual Geometry Group, where its creators are based. It has achieved excellent results in tasks such as image classification and has made significant contributions to the development of deep learning.
The biggest characteristic of VGG is that it stacks the neural network by using 3×3 size convolutional kernels. Due to the use of smaller convolutional kernels and pooling layers, VGG exhibits good robustness to variations in input images and can adapt to images of different scales and deformations. This article uses VGG-16 to extract global deep features. The network structure of VGG-16, as shown in Fig. 2, consists of thirteen convolutional layers, five pooling layers, and three fully connected layers.
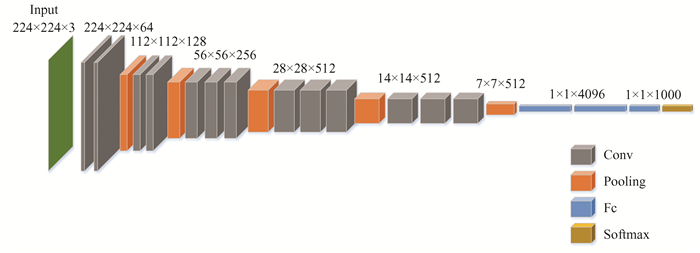
|
Fig.2 VGG architecture |
1) Convolutional layers: The convolutional layer is the core of convolutional neural networks, which achieves feature extraction and representation of input data through convolutional operations. During the convolution process, the convolutional kernel performs a weighted sum on a local region of the input data, producing a feature value as output. The size and number of convolutional kernels can be designed and adjusted according to the specific task and network structure. The convolutional layer is typically processed by a nonlinear activation function to make the features in the feature maps more robust and informative. In addition, to prevent overfitting, the convolutional layer performs regularization operations such as dropout and batch normalization. The specific convolution process is as follows:
| $ x^l=g\left(\sum x^{l-1} * W^l+b^l\right) $ |
where g(·) and * represent the activation function and convolution operation, Wl and bl represent the weights and biases of the lth layer, xl-1 and xl represent the input and output feature maps of the lth layer, respectively.
2) Pooling layers: Pooling operations are usually performed after the convolutional layer to downsample the feature maps and preserve the most significant features. Pooling layers typically have few parameters, only the size of the pooling window and stride, which can be adjusted and designed according to the specific task and network structure. By using pooling layers, the network can effectively reduce the size of feature maps and the number of model parameters while retaining important features, thereby improving the efficiency and generalization ability of the model. There are usually two types of pooling operations: max pooling and average pooling. The specific pooling operation is shown below:
| $ x^l=g\left(\operatorname{down}\left(x^{l-1}\right)+b^l\right) $ |
3) Fully connected layers: Usually, after convolutional layers and pooling layers, the fully connected layers are used to connect all the feature maps from the previous layers into a 1-D vector and map it to the output layer for classification and prediction.
1.3 Local Edge Feature Extraction by HOGAlthough the VGG network can extract global deep features, it severely loses local edge features, resulting in incomplete feature representation and ultimately affecting classification performance. Therefore, to address this issue, this article uses HOG to extract local edge features and combines them with the deep features extracted by VGG.
HOG is based on the direction and intensity information of local image gradients, and it can effectively describe the local edge features in PolSAR images. The main steps are as follows:
1) Image normalization: The input image is normalized using the gamma correction method to reduce the impact of local variations in PolSAR images and weaken the interference of speckle noise. The formula is defined as
| $ \boldsymbol{I}(x, y)=\boldsymbol{I}(x, y)^{\mathrm{gamma}} $ |
2) Gradients calculation: The amplitude and direction of the gradient are as follows:
| $ \begin{gathered} \boldsymbol{G}(x, y)=\sqrt{G_x^2(x, y)+G_y^2(x, y)} \\ \boldsymbol{\alpha}(x, y)=\arctan \left[\frac{G_x(x, y)}{G_y(x, y)}\right] \end{gathered} $ |
where G(x, y) and α(x, y) denote the gradient amplitude and direction, Gx(x, y) and Gy(x, y) denote the horizontal and vertical gradients at pixel (x, y), respectively.
3) Image segmentation: The image is divided into multiple small cells with identical dimensions, each containing 64 pixels (8 × 8), which are used for subsequent calculations.
4) Gradient histogram calculation of each cell: For each cell, first, compute the gradient magnitude and direction of all pixels inside it. Then, divide the gradient direction into 9 bins, each covering a 20° range. For each pixel, add its gradient magnitude to the bin corresponding to its gradient direction. Finally, sum up the values of all pixels to obtain the gradient histogram of the small cell.
5) Feature descriptor calculation of each block: Slide adjacent 4 cells with a certain stride to form a block. For each block, connect the gradient histograms of all cells inside to form a feature vector. Then normalize the feature vector of each block to eliminate the influence of lighting, shadow, and other factors on the gradient.
6) Feature descriptors integration of all blocks: Concatenate the feature vectors of all blocks to obtain the final HOG feature vector.
1.4 Optimal Feature Fusion and Final ClassificationAfter obtaining the global deep features and the local edge features, it is not advisable to simply stack them, or it may lead to information redundancy and underutilization. Therefore, this article designs a feature fusion strategy to optimally fuse the global deep features and the local edge features.
Assuming the global deep features are [f1, f2, …, fn1] and the local edge features are [h1, h2, …, hn2]. Then these features can be optimally fused into a feature vector V through the following approach:
| $ \begin{gathered} \boldsymbol{V}=\boldsymbol{G} \cdot \boldsymbol{\alpha} \\ \boldsymbol{G}=\left[f_1, f_2, \cdots, f_{n_1}, h_1, h_2, \cdots, h_{n_2}\right] \\ \boldsymbol{\alpha}=\left[\alpha_1, \alpha_2, \cdots, \alpha_{n_1}, \alpha_{n_1+1}, \alpha_{n_1+2}, \cdots, \alpha_{n_1+n_2}\right] \end{gathered} $ |
where α represents the fusion weight. And the update of α is achieved by minimizing the loss function E, as shown below:
| $ \alpha_1, \alpha_2, \cdots, \alpha_{n_1+n_2}=\operatorname{argmin}(E) $ |
Then, the fused vector V is fed into a fully connected layer to transform it into a 1-D vector. The specific operation is as follows:
| $ Z=\sigma(\boldsymbol{V} \cdot \omega+\beta) $ |
where ω represents the weight, β represents the deviation and σ(·) represents the activation function.
In addition, this article uses the cross-entropy function as the loss function to optimize the training process. The formula is as follows:
| $ E(y, \hat{y})=-\sum\limits_{i=1}^k y_i \log \hat{y}_i $ |
where yi and
Finally, this article uses the softmax classifier to classify different terrain categories. The softmax classifier is a common algorithm for multi-class classification. It maps each input vector to a probability distribution, where each category is assigned a probability value and the sum of all probability values is equal to 1. Suppose the input of the classifier is [Z1, Z2, ···, ZN], then the posterior probability of each category can be calculated using the following formula:
| $ p_i=\frac{\exp \left(Z_i\right)}{\sum\limits_{j=1}^k \exp \left(Z_j\right)} $ |
This article uses three real PolSAR datasets to evaluate and analyze the actual terrain classification performance of the proposed HOG-VGG method. First, the Flevoland dataset is a L-band PolSAR data, which was collected by the NASA/JPL ARISAR platform from the Flevoland region. It mainly contains thirteen terrain categories with a size of data of 750×1024. The Pauli RGB image of the Flevoland dataset is illustrated in Fig. 3(a).

|
Fig.3 Pauli RGB images of PolSAR datasets |
The second dataset is San Francisco, which is a L-band PolSAR data acquired by the NASA/JPL ARISAR platform from San Francisco region. This dataset has a size of 470×880, and it mainly contains five terrain categories. The Pauli RGB image of the San Francisco dataset is illustrated in Fig. 3(b).
The third dataset is Oberpfaffenhofen, which is a L-band fully polarized radar data obtained by the E-SAR sensor from the German Aerospace Center. This dataset has a size of 1300×1200, and it mainly contains three terrain categories. The Pauli RGB image of the Oberpfaffenhofen dataset is illustrated in Fig. 3(c).
2.2 Experimental DesignTo demonstrate the superiority of the HOG-VGG method in the field of PolSAR terrain classification, this article uses some common methods for comparison, which are Dc-CNN, CV-CNN, ResNet, VGG and HOG+SVM. Specifically, for each method, we conduct experiments with different parameter settings to evaluate their classification performance.
1) As for Dc-CNN, the first channel is composed of three convolutional layers, and each layer has a kernel size of 5×5. Meanwhile, the second channel is composed of two convolutional layers, and each layer has a kernel size of 6×6.
2) As for CV-CNN, the input data is represented using a 6-D complex number format, containing a total of 5184 independent units of information.
3) As for VGG and ResNet, select VGG-16 and ResNet-18 for comparative experiments.
4) As for HOG+SVM, the penalty coefficient of the error term is set to 1, and the algorithm utilizes a linear kernel function with a specific gamma value of 0.1.
5) As for the proposed HOG-VGG, the VGG network is used to extract the global deep features, which is composed of thirteen convolutional layers, five pooling layers, and three fully connected layers. The convolutional neural network, which is used to process the local edge features extracted by HOG, is composed of a convolutional layer, a pooling layer, and a fully connected layer.
6) For each method, the input PolSAR image slices are 15×15. The convolutional layers use a stride of 1, while the pooling layers use a stride of 2. The batch size is 64, and the training epoch is 100. Additionally, we randomly choose 0.5% of the total samples for the training set.
To ensure the credibility of the experiments and the accuracy of the results, all experiments are running on the same device, which consists of a six-core Intel Core i7-11750H CPU with a frequency of 3.20 GHz, 16.0 GB of memory, and an Nvidia GeForce RTX 2080 GPU with a frequency of 2.50 GHz and 8.0 GB of memory. And the deep learning framework used in this article is TensorFlow.
2.3 Evaluation MetricsOverall Accuracy (OA) and Kappa coefficient (Kappa) are common metrics for evaluating the actual performance of classification algorithms. OA refers to the proportion of correctly classified samples, which can help us understand the overall classification ability of the classifier. And Kappa is a more comprehensive evaluation metric, which not only considers the classifier's classification accuracy, but also takes into account the impact of random errors in the classification results. In addition, the larger the values of OA and Kappa, the better the classification performance. The mathematical definitions are shown as
| $ \mathrm{OA}=\frac{M}{N} $ |
where M represents the sum of the diagonal elements, N represents the sum of all the elements in the matrix.
| $ \text { Kappa }=\frac{\mathrm{OA}-P}{1-P}\\ P=\frac{1}{N^2} \sum\limits_{i=1}^C \bar{Z}(i, :) * \bar{Z}(:, i) $ |
where Z(i, : ) and Z(: , i) represent the sum of the elements in ith row and ith column of the confusion matrix, respectively.
Therefore, these evaluation metrics can provide a comprehensive and accurate evaluation of the classification algorithms.
2.4 Classification Results and Analysis1) Classification experiments on the Flevoland dataset: The classification results of different methods on the Flevoland dataset are shown in Fig. 4. Compared to other classification methods, HOG-VGG has less misclassification points, which means it performs more accurately and reliably in classification tasks. In addition, HOG-VGG exhibits better continuity while maintaining high classification accuracy. By observing the regions marked with red circles in Figs. 4(b)-(g), it is clear that HOG-VGG has the best classification performance, which further demonstrates the superiority of HOG-VGG. The proposed HOG-VGG effectively enhances the feature representation completeness, so the classification performance is greatly improved.
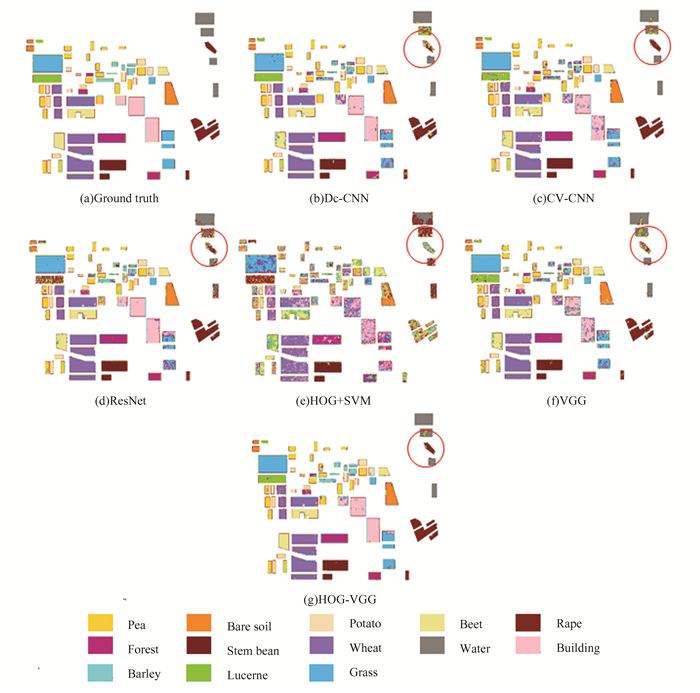
|
Fig.4 Classification results of different methods on the Flevoland dataset |
To assess the actual classification performance of different classification methods on each category of the Flevoland dataset, Fig. 5 shows the confusion matrices of different classification methods. Confusion matrix is a visual tool for evaluating classification performance, where the rows correspond to the true categories, the columns correspond to the predicted categories, and the diagonal elements represent the number of correctly classified samples.
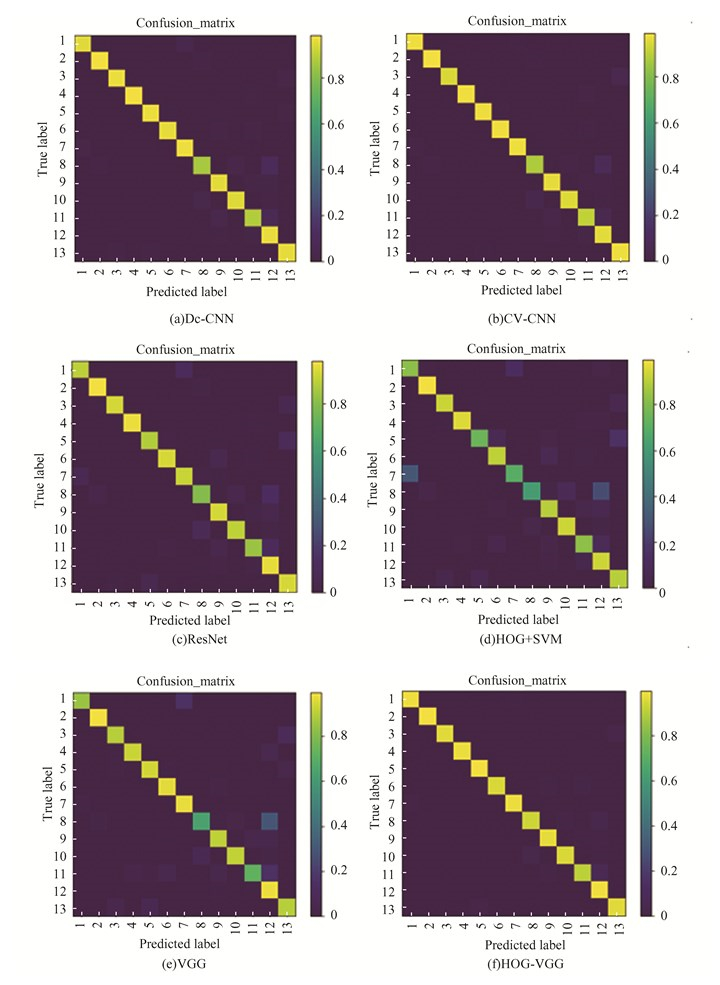
|
Fig.5 Confusion matrix of different methods on the Flevoland dataset |
Based on the comparative analysis of different confusion matrices, it can be found that, compared to HOG-VGG, Dc-CNN, CV-CNN, ResNet and VGG, have relatively lower accuracy in certain categories. These methods can only extract the deep features of PolSAR images, but ignore the local edge features, which are very important in PolSAR image classification, leading to unsatisfactory classification results. However, HOG-VGG performs well on each category. This indicates that HOG-VGG is an effective classification method, demonstrating better performance on the Flevoland dataset than other methods.
Table 1 lists the specific classification accuracy of different methods for each category. Based on the data in Table 1, we can draw the following conclusion.
| Table 1 Classification accuracy of different methods on the Flevoland dataset |
The Kappa values of HOG+SVM, VGG and HOG-VGG are 80.47%, 89.57% and 97.21%, respectively, and it is evident that HOG-VGG has the largest one. Moreover, the classification accuracy of HOG-VGG is also higher on each category, which means that under the same experimental conditions, HOG-VGG has better classification performance than HOG+SVM and VGG. This result demonstrates that combining HOG descriptor with VGG network can greatly improve the performance of PolSAR terrain classification.
In addition, the Kappa values of Dc-CNN, CV-CNN, and ResNet are 94.73%, 95.21%, and 90.41%, respectively. It is obvious that the classification performance of these advanced algorithms is relatively poor. The reason is that these methods have complex network structures with a large number of network parameters, resulting in low accuracy when the sample size is small. However, the proposed HOG-VGG has distinct differences and innovations compared to these methods. HOG-VGG has a unique advantage in addressing the low classification accuracy of small-sample data by introducing additional local edge features, namely HOG features. By optimally integrating global deep features with local edge features, HOG-VGG is able to improve the classification capability significantly. Compared to other methods, HOG-VGG can better capture subtle features and edge information in the samples, leading to more accurate classification.
2) Classification experiments on the San Francisco dataset: The classification maps of different methods are shown in Fig. 6. By observing the regions marked with red rectangles in Figs. 6(b)-(g), obviously, the similarity between the classification map of HOG-VGG and the ground truth is the highest. By comparison, there are more misclassified regions in the classification maps of other methods, which indicates that integrating local edge features into the VGG network is very helpful for PolSAR terrain classification.

|
Fig.6 Classification results of different methods on the San Francisco dataset |
Besides, the classification maps show that the developed urban has the worst classification performance across all categories, and it is mainly misclassified as vegetation. The reason is that the global deep features of these two categories are highly similar, and to distinguish them, it mainly relies on local edge features. Compared to other methods, HOG-VGG combines local edge features with global features, so it has better classification performance in developed urban.
Table 2 lists the specific classification accuracy of different methods for each category. As shown in Table 2, HOG-VGG achieves the highest classification accuracy on each category, especially on the developed urban, which is significantly higher than other methods. Furthermore, the values of Kappa and OA of HOG-VGG is 93.27% and 94.63%, respectively, which are at least 3.80% and 2.27% higher than other methods. These results demonstrate that the optimal fusion of global deep features and local edge features provides an effective solution to the problem of low classification accuracy when dealing with small-sample data.
| Table 2 Classification accuracy of different methods on the San Francisco dataset |
3) Classification experiments on the Oberpfaffenhofen dataset: To ensure that the proposed HOG-VGG can perform well in different datasets and application scenarios, we conducted additional experiment on the Oberpfaffenhofen dataset. By comparing the classification maps of different methods in Fig. 7, it is evident that HOG-VGG exhibits superiority. HOG-VGG demonstrates the best performance in the classification results for each category, which can be attributed to the effective combination of deep features and local edge features, thereby enhancing the integrity of feature representation. This comprehensive feature representation makes the differences between each category more pronounced, making it easier to distinguish different terrain categories.
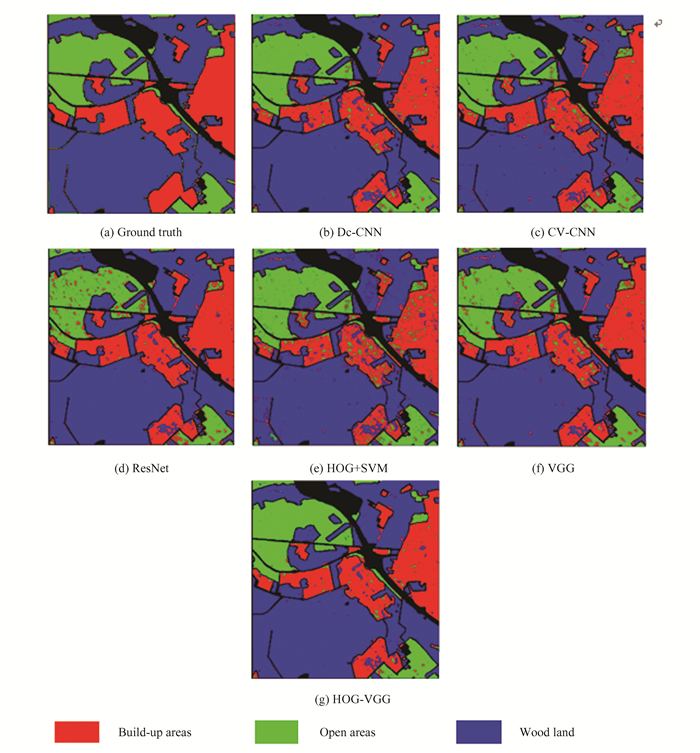
|
Fig.7 Classification results of different methods on the Oberpfaffenhofen dataset |
The same conclusion can be drawn from Table 3. As shown in Table 3, HOG-VGG has the highest classification accuracy among three categories, and its OA and Kappa value are also higher than other methods. These experimental results strongly demonstrate the superiority of HOG-VGG.
| Table 3 Classification accuracy of different methods on the Oberpfaffenhofen dataset |
2.5 Evaluation of the Proposed HOG-VGG
In this part, receiver operation characteristics (ROC) and area under the ROC curve (AUC) are used to accurate compare and evaluate the actual performance of different methods in PolSAR terrain classification. ROC curve provides a visual representation of the performance of the classification algorithm by plotting the relationship between true positive rate (TPR) and false positive rate (FPR) at different classification thresholds. AUC provides a single numerical value to measure the overall classification ability of the classification algorithm at different thresholds. Normally, greater AUC values indicate superior classification performance.
Fig. 8 shows the ROC curves and corresponding AUC values of different methods on two PolSAR datasets. Based on the results shown in Fig. 8, it can be observed that HOG-VGG performs better in PolSAR terrain classification. Specifically, HOG-VGG has a higher TPR and a lower FPR. Furthermore, among all classification methods, HOG-VGG also achieves the highest AUC value. Other advanced classification algorithms except HOG-VGG ignore the local edge features that are crucial for PolSAR image classification, resulting in incomplete feature representation and relatively poor classification performance. These results indicate that HOG-VGG is an effective PolSAR terrain classification method and has a broad application prospect.
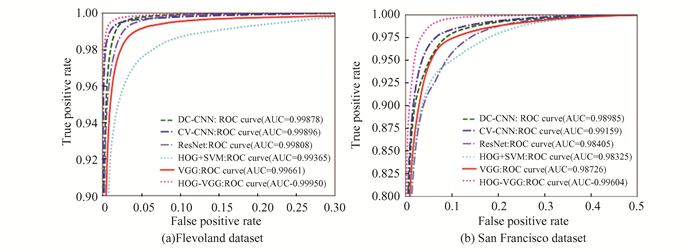
|
Fig.8 ROC curves and AUC values of different methods in different datasets |
3 Conclusions
In this article, a novel algorithm named HOG-VGG is proposed for PolSAR terrain classification. HOG-VGG combines the deep convolutional neural network VGG with traditional feature extraction method HOG, aiming to fully utilize the information embedded in PolSAR images. We design a feature fusion strategy to optimally fuse the global deep features extracted by VGG and the local edge features extracted by HOG. Through this fusion approach, the integrity of feature representation is effectively enhanced, and the classification accuracy and generalization capability are greatly improved. In the experiments, we employ three real PolSAR datasets and compare our method, HOG-VGG, against other state-of-the-art classification methods. The results demonstrate that HOG-VGG outperforms the others in all evaluation metrics, confirming its effectiveness and superiority in PolSAR terrain classification tasks. Therefore, we have reasons to believe that HOG-VGG has a broad application prospect and it is worth for further research and application.
In the future, we will strive to search for and improve more efficient edge feature extraction algorithms to address the computational complexity issue of the HOG method. Additionally, PolSAR data is collected periodically at certain time intervals, and this multi-temporal characteristic provides richer and more comprehensive information for terrain classification. We will utilize these multi-temporal data and combine them to enhance the richness of the data and achieve better classification results.
| [1] |
Pierce L E, Ulaby F T. Knowledge-based classification of polarimetric SAR images. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1081-1086. DOI:10.1109/36.312896 (  0) 0) |
| [2] |
Cloude R S, Papathanassiou K. Polarimetric SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551-1565. DOI:10.1109/36.718859 (  0) 0) |
| [3] |
Yamaguchi Y, Yajima Y, Yamada H. A four-component decomposition of POLSAR images based on the coherency matrix. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 292-296. DOI:10.1109/LGRS.2006.869986 (  0) 0) |
| [4] |
Geng J, Deng X, Ma X, et al. Transfer learning for SAR image classification via deep ioint distribution adaptation networks. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5377-5392. DOI:10.1109/TGRS.2020.2964679 (  0) 0) |
| [5] |
Liu F, Jiao L, Tang X, et al. Local restricted convolutional neural network for change detection in polarimetric SAR images. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(3): 818-833. DOI:10.1109/TNNLS.2018.2847309 (  0) 0) |
| [6] |
Liu G, Zhang X, Meng J. A small ship target detection method based on polarimetric SAR. Remote Sensing, 2019, 11(24): 2938. DOI:10.3390/rs11242938 (  0) 0) |
| [7] |
Bi H, Sun J, Xu Z. A Graph-based semisupervised deep learning model for PolSAR image classification. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(4): 2116-2132. DOI:10.1109/TGRS.2018.2871504 (  0) 0) |
| [8] |
Wang J, Hou B, Jiao L. Representative learning via span-based mutual information for PolSAR image classification. Remote Sensing, 2021, 13(9): 1609. DOI:10.3390/RS13091609 (  0) 0) |
| [9] |
Wang J, Hou B, Ren B, et al. Parameter selection of Touzi decomposition and a distribution improved autoencoder for PolSAR image classification. ISPRS Journal of Photogrammetry and Remote Sensing, 2022, 186: 246-266. DOI:10.1016/J.ISPRSJPRS.2022.02.003 (  0) 0) |
| [10] |
Demirci S, Kirik O, Ozdemir C. Interpretation and analysis of target scattering from fully-polarized ISAR images using Pauli decomposition scheme for target recognition. IEEE Access, 2020, 8: 155926-155938. DOI:10.1109/ACCESS.2020.3018868 (  0) 0) |
| [11] |
Freeman A, Durden S L. Three-component scattering model to describe polarimetric SAR data. Radar Polarimetry, 1748, 213-225. DOI:10.1117/12.140618 (  0) 0) |
| [12] |
Cloude S R, Pottier E. A review of target decomposition theorems in radar polarimetry. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518. DOI:10.1109/36.485127 (  0) 0) |
| [13] |
Touzi R, Charbonneau F. Characterization of target symmetric scattering using polarimetric SARs. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2507-2516. DOI:10.1109/TGRS.2002.805070 (  0) 0) |
| [14] |
Cloude S R, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78. DOI:10.1109/36.551935 (  0) 0) |
| [15] |
Krogager E. Properties of the sphere, diplane, helix (target scattering matrix decomposition). Molecular Ecology, 2006, 15(11): 3205-3217. (  0) 0) |
| [16] |
Yamaguchi Y, Moriyama T, Ishido M, et al. Four-component scattering model for polarimetric SAR image decomposition. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706. DOI:10.1109/TGRS.2005.852084 (  0) 0) |
| [17] |
Cameron W L, Leung L K. Feature motivated polarization scattering matrix decomposition. IEEE International Conference on Radar. Piscataway: IEEE, 1990: 549-557. DOI: 10.1109/RADAR.1990.201088.
(  0) 0) |
| [18] |
Zou T, Yang W, Dai D, et al. Polarimetric SAR image classification using multi-features combination and extremely randomized clustering forests. EURASIP Journal on Advances in Signal Processing, 2010, Article number: 465612. DOI:10.1155/2010/465612 (  0) 0) |
| [19] |
Uhlmann S, Kiranyaz S. Integrating color features in Polarimetric SAR image classification. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 2197-2216. DOI:10.1109/TGRS.2013.2258675 (  0) 0) |
| [20] |
De Grandi G D, Lee J S, Schuler D L. Target detection and texture segmentation in Polarimetric SAR images using a wavelet frame: theoretical aspects. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3437-3453. DOI:10.1109/TGRS.2007.905103 (  0) 0) |
| [21] |
Comaniciu D, Meer P. Mean shift analysis and applications. Proceedings of the Seventh IEEE International Conference on Computer Vision. Piscataway: IEEE, 1999: 1197-1203. DOI: 10.1109/ICCV.1999.790416.
(  0) 0) |
| [22] |
Kersten P R, Lee J S, Ainsworth T L. Unsupervised classification of polarimetric synthetic aperture Radar images using fuzzy clustering and EM clustering. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 519-527. DOI:10.1109/TGRS.2004.842108 (  0) 0) |
| [23] |
Gadhiya T, Roy A K. Superpixel-driven optimized wishart network for fast PolSAR image classification using global K-means algorithm. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 97-109. DOI:10.1109/TGRS.2019.2933483 (  0) 0) |
| [24] |
Parikh H, Patel S, Patel V. Classification of SAR and PolSAR images using deep learning: A review. International Journal of Image and Data Fusion, 2020, 11(1): 1-32. DOI:10.1080/19479832.2019.1655489 (  0) 0) |
| [25] |
Gupta S, Kumar S, Garg A, et al. Class wise optimal feature selection for land cover classification using SAR data. IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Piscataway: IEEE, 2016: 68-71. DOI: 10.1109/IGARSS.2016.7729008.
(  0) 0) |
| [26] |
Tao C, Chen S, Li Y, et al. PolSAR land cover classification based on roll-invariant and selected hidden polarimetric features in the rotation domain. Remote Sensing, 2017, 9(7): 660-680. DOI:10.3390/rs9070660 (  0) 0) |
| [27] |
Fukuda S, Hirosawa H. Support vector machine classification of land cover: Application to polarimetric SAR data. IEEE International Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2001: 187-189. DOI: 10.1109/IGARSS.2001.976097.
(  0) 0) |
| [28] |
Sun Y, Liu Z, Todorovic S, et al. Adaptive boosting for SAR automatic target recognition. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 112-125. DOI:10.1109/TAES.2007.357120 (  0) 0) |
| [29] |
Geng J, Jiang W, Deng X. Multi-scale deep feature learning network with bilateral filtering for SAR image classification. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 167: 201-213. DOI:10.1016/j.isprsjprs.2020.07.007 (  0) 0) |
| [30] |
Zhou Y, Wang H, Xu F, et al. Polarimetric SAR image classification using deep convolutional neural networks. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1935-1939. DOI:10.1109/LGRS.2016.2618840 (  0) 0) |
| [31] |
Hua W, Wang S, Xie W, et al. Dual-Channel convolutional neural network for polarimetric SAR images classification. IEEE International Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2019: 3201-3204. DOI: 10.1109/IGARSS.2019.8899103.
(  0) 0) |
| [32] |
Liu X, Jiao L, Tang X, et al. Polarimetric convolutional network for PolSAR image classification. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(5): 3040-3054. DOI:10.1109/TGRS.2018.2879984 (  0) 0) |
| [33] |
Qin R, Fu X, Lang P. PolSAR image classification based on low-frequency and contour subbands-driven polarimetric SENet. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 4760-4773. DOI:10.1109/JSTARS.2020.3015520 (  0) 0) |
| [34] |
Zhang Z, Wang H, Xu F, et al. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7177-7188. DOI:10.1109/TGRS.2017.2743222 (  0) 0) |
| [35] |
Wang L, Hong H, Zhang Y, et al. PolSAR-SSN: An end-to-end superpixel sampling network for PolSAR image classification. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. DOI:10.1109/LGRS.2022.3152794 (  0) 0) |
| [36] |
Ding L, Zheng K, Lin D, et al. MP-ResNet: Multipath residual network for the semantic segmentation of high-resolution PolSAR images. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. DOI:10.1109/LGRS.2021.3079925 (  0) 0) |
| [37] |
Wen Z, Wu Q, Liu Z, et al. Polar-spatial feature fusion learning with variational generative-discriminative network for PoLSAR classification. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8914-8927. DOI:10.1109/TGRS.2019.2923738 (  0) 0) |
| [38] |
Matt D, Ferat S. HOG feature human detection system. IEEE International Conference on Systems, Man, and Cybernetics (SMC). Piscataway: IEEE, 2016: 2878-2883. DOI: 10.1109/SMC.2016.7844676.
(  0) 0) |
 2024, Vol. 31
2024, Vol. 31


