Foam aluminum, composed of aluminum metal or its alloys, is characterized by its porous nature, numerous voids, and a honeycomb-like structure[1-3].Developing precise and comprehensive performance evaluation methods is urgently required to enhance the utilization of foam aluminum.
The Gibson-Ashby formula[4]and the Hanssen formula[5], introduced by Gibson and Ashby, hold significance as traditional equations for describing the mechanical characteristics of porous materials. Nevertheless, foam aluminum displays diverse microstructures and is affected by various structural factors, such as porosity, pore size, and pore distribution[6].The majority of these conventional constitutive relationships are macroscopic phenomenological models that do not account for the influence of pore structures[7-8].Furthermore, foam aluminum may have distinct performance requirements in different application scenarios. Consequently, evaluation methods must be tailored to meet specific application requirements. Additionally, the foam aluminum field lacks standardized testing methods and performance parameters, leading to challenges in comparing and validating findings across different studies. In summary, traditional methods fail to establish a correlation between the microstructural attributes of foam aluminum and its mechanical characteristics or to precisely model and forecast foam aluminum's mechanical properties within parameter space. Relying solely on a macroscopic perspective for evaluating foam aluminum's mechanical properties no longer meets the contemporary performance design demands. The establishment of a mapping relationship between foam aluminum's structural parameters and its mechanical characteristics is a pressing and pivotal matter.
Machine learning is a data-driven approach for precise data prediction and has found extensive applications across various domains. Data-driven techniques have emerged as crucial instruments in the investigation of multiscale materials[9-11].International researchers have endeavored to employ machine learning techniques for a more precise assessment of foam aluminum's mechanical characteristics. In 2013, scientists at Isfahan University of Technology, including Jamshidi-Alashti et al.[12], employed the Artificial Neural Network (ANN) technique to establish correlations between foaming process parameters and compressive mechanical attributes. They forecasted the alterations in the material's mechanical properties concerning variations in pore size across different foaming processes. In 2023, scientists at the University of Indonesia, including Fatriansyah and Suhariadi[13], employed artificial neural networks to investigate the correlation between alloy composition and mechanical attributes. They established both linear and nonlinear associations between element composition and the mechanical properties of high-temperature alloys. Nevertheless, based on the current information, there is no research application employing machine learning techniques for assessing the mechanical properties of foam aluminum based on its structural parameters.
In this study, we employed Naive Bayes[14], Random Forest[15], and GRNN[16] for the modeling process. A GRNN model with an accuracy of up to 87.46% was chosen. Subsequently, we carried out feature learning, feature selection[17-18], and importance assessment[19-20]. Upon recognizing key features, we conducted feature weight analysis and residual weight allocation to establish the WEP formula for equivalent porosity. Lastly, we validated this formula using compressive data from multiple foam aluminum samples. During the validation phase, we employed 11 sets of foam aluminum data from four research institutions worldwide. WEP demonstrated exceptional accuracy. In comparison to the Gibson-Ashby formula, the WEP formula takes into account a more comprehensive range of crucial structural factors, resulting in more precise parameters. Its evaluation accuracy improved by 18.18% in contrast to the Gibson-Ashby formula. In contrast to the research conducted by Jamshidi-Alashti et al.[12] from Isfahan University and Fatriansyah and Suhariadi[13] from the University of Indonesia, our study employed the Generalized Regression Neural Network (GRNN) method to model the microstructural feature data and mechanical performance data of foam aluminum. In contrast to ANN, GRNN exhibits superior generalization and adaptability to data, particularly when handling small or noisy datasets[21]. Conversely, ANN necessitates the adjustment of numerous parameters, such as learning rates, the quantity, and dimensions of hidden layers. In comparison, GRNN does not necessitate intricate parameter tuning during training and use.
This paper illustrates the practicality of utilizing machine learning methods for evaluating the mechanical properties of foam aluminum using its structural parameters, thus broadening the application domain of deep learning in materials research.
1 Research MethodTo address the aforementioned issues, the GRNN method from the field of computer science is incorporated in this study. The complex and typically nonlinear relationship between foam aluminum's mechanical properties and its microstructure is challenging to model using traditional linear methods. This intricate relationship can be effectively captured by the GRNN, which excels in nonlinear modeling. GRNN, an autonomously feature-selecting, data-driven method, improves model interpretability and accuracy when handling datasets with multiple features. It is adaptable to various contexts and does not rely on specific theoretical models. The robustness and versatility of GRNN, demonstrated across domains, underscore its track record of success. In summary, GRNN provides a reliable choice for analyzing the pore characteristics and performance of foam aluminum, offering flexible nonlinear modeling, feature selection, importance assessment, and high robustness.
Firstly, a detailed analysis and cleansing of the foam aluminum data were conducted to ensure data accuracy and reliability[22]. Subsequently, modeling was performed on the microstructural characterization data and mechanical performance data of foam aluminum. Feature learning, feature selection, and importance assessment were enabled by employing GRNN, facilitating the identification of significant features related to foam aluminum's characterization indicators and conducting importance evaluation of these indicators. In this study, a novel characterization parameter called equivalent porosity was proposed to represent the relationship between the microstructural features and performance of foam aluminum. This parameter was derived from the weighted distribution of features such as porosity, average pore size, and circularity of foam aluminum. Through experimental verification on foam aluminum samples, it has been demonstrated that the equivalent porosity, as a new characterization parameter, provides a more accurate reflection of foam aluminum's performance.
2 Research Content 2.1 Aluminum Foam Structure IntroductionLooking from the perspective of pore openness, we can categorize foam aluminum into two structural types: open-cell structure and closed-cell structure[23]. The open-cell structure of foam aluminum exhibits interconnected pores, forming a continuous foam structure where pores link together[24]. This interconnected structure facilitates the free flow of gases and liquids through foam aluminum, as Figs. 1(a) and 1(c) illustrate. The pore sizes within this structure usually span from 0.1 mm to several millimeters, with porosity ranging from 50% to 75%, density ranging from 0.68 to 1.35 g/cm3, and a through-hole percentage ranging from 10% to 35%. Conversely, the closed-cell structure of foam aluminum comprises isolated pores that lack direct connections between them, as shown in Figs. 1(b) and 1(d). In this type of foam aluminum, each pore exists in isolation, resulting in a non-interconnected pore network. The pore sizes within closed-cell foam aluminum generally range from 0.5 mm to several millimeters, with porosity ranging from 50% to 95% and a density range of 0.68 to 1.35 g/cm3.From the perspective of pore shape, we can categorize foam aluminum into two distinct types: non-spherical pores and spherical pores. The non-spherical pore structure is characterized by uneven pore sizes and rough pore walls, mainly composed of polygonal or irregular particles. The pore structure is formed as these particles interact through electrostatic forces or van der Waals forces. The non-spherical pore structure is typically found on the surface or edges of foam aluminum, enhancing properties such as protection. Due to the non-uniformity of pore sizes, foam aluminum exhibits a relatively higher porosity, as shown in Fig. 1(c). This structural configuration is frequently encountered in methods involving infiltration-based preparation. On the other hand, spherical pores denote that the pores within foam aluminum are nearly spherical or exhibit a spherical shape. The spherical pore structure is characterized by uniform pore sizes and smooth pore walls, primarily composed of small spherical particles. The pore structure is formed as these particles are attracted to each other through van der Waals forces[25]. This structural characteristic is typically observed in foam aluminum produced through gas foaming methods, as demonstrated in Fig. 1(d). Foam aluminum featuring spherical pores exhibits a highly uniform distribution of these pores.

|
Fig.1 CT images of different types of aluminum foam samples and their sample |
2.2 Characterization Parameters of Aluminum Foam 2.2.1 Porosity
The porosity of foam aluminum is defined as the ratio of the volume of internal pores to the total volume of the material[25]. Porosity serves as an important characterization indicator for foam aluminum, as it directly reflects the material's porous nature and pore structure. Typically, it is expressed as a percentage and can be calculated using the following formula:
| $ P=\frac{V_1}{V_2} \times 100 \%=\left(1-\frac{\rho_1}{\rho_2}\right) \times 100 \% $ | (1) |
Eq. (1) defines the porosity of the foam aluminum sample, where P represents it[26]. The pore volume, denoting the total volume of the pore space within the foam aluminum matrix, is represented by V1. V2 stands for the matrix volume, which is the total volume of the foam aluminum sample. The density of the aluminum matrix is represented by ρ2, and ρ1 represents the density of the foam aluminum sample.
2.2.2 Average pore sizeThe average pore size of foam aluminum, which refers to the average size of the internal pores within the material[27], is an important indicator for evaluating the pore structure and pore distribution of foam aluminum. Various methods can be employed to calculate the average pore size of foam aluminum, with the most commonly used approach being through pore size distribution functions. Common pore size distribution functions include cumulative distribution functions and probability density functions. In the cumulative distribution function, the pore size distribution of the foam aluminum sample is summed up, and the average value of this function is calculated to obtain the average pore size of the foam aluminum[28]. The calculation function is expressed as follows:
| $ F_X(x)=\int_{-\infty}^x f(t) \mathrm{d} t $ | (2) |
where x is a random variable and f(t) represents the cumulative distribution function of X.
The probability density function involves statistical analysis being performed on the pore size distribution of the foam aluminum sample to obtain the probability density function of the pore sizes[29]. By calculating the weighted average of the probability density function, the average pore size can be determined. The calculation function is expressed as follows:
| $ f_X(x)=\frac{1}{\sigma \sqrt{2 \mathtt{π}}} \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}} $ | (3) |
where x is the random variable, μ is the mean value of the random variable, and σ is the standard deviation of the random variable.f(x) represents the cumulative distribution function of X.
2.2.3 Pore wall thicknessThe thickness of the pore structure within foam aluminum material is referred to as pore wall thickness[30]. It is an important parameter for characterizing the pore structure of foam aluminum and is known to directly influence its mechanical and thermal conductivity properties. Methods for the measurement and calculation of pore wall thickness include microscopic observation and image processing.
2.2.4 Form factorThe parameter known as the pore shape factor in foam aluminum is used to describe the shape of the internal pores[31]. It refers to the degree of deviation between the actual shape of the pores in foam aluminum and a perfect sphere, and it can be utilized to measure the irregularity of the pores. Typically, the shape factor is calculated as the ratio of the actual pore area to the pore perimeter. The calculation can be done using the following formula:
| $ F=\frac{4 \mathtt{π} S}{C^2} $ | (4) |
where F is the shape factor, S is the cross-sectional area of the pore, and C is the perimeter of the pore.
2.2.5 Pore distributionThe pore distribution in foam aluminum refers to the spatial arrangement of pores within the material. It can be classified into uniform distribution, random distribution, and non-uniform distribution[32]. Various characterization methods, such as pore diameter distribution, pore volume distribution, pore spacing distribution, and pore shape distribution, can be employed to describe and analyze the pore distribution in foam aluminum.
2.2.6 AnisotropyAnisotropy is defined as the ratio of 1 minus the minimum eigenvalue to the maximum eigenvalue of the covariance matrix of a porous structure, and it can measure the deviation of an object from being perfectly spherical. According to the definition of anisotropy in this paper, the anisotropy value of ideal spherical pores is 0. In contrast to sphericity, anisotropy emphasizes the differences in chord lengths of pores in different directions. By calculating the anisotropy of foam aluminum, the overall structural orientation within the foam aluminum and its relationship with compressive performance can be assessed.
2.3 Data Set Creation 2.3.1 Source data sourceThe experimental data for this study were collected and compiled from foam aluminum samples obtained over the years by our research group. The collected data include characterization parameters such as porosity, average pore diameter, pore wall thickness, shape factor, and pore distribution, as well as compression test data of the samples. A total of 7 attributes were extracted, resulting in 18163 instances. After data cleaning was performed on the initial extracted dataset, the remaining samples amounted to 14886. The dataset was divided into a training set, comprising 80% of the samples (11906 samples), and a testing set, comprising 20% of the samples (2980 samples).
2.3.2 Data set creationFirstly, it is necessary for outliers and missing values in the dataset to be handled. The porosity is represented as the percentage of pore volume to the total volume of the bulk foam aluminum in its natural state, and its value is kept below 1. The pore size is defined as the shape and size of the pore channels in the porous solid. While the pores in foam metals are extremely irregular, they are often approximated as circular, and the pore size is characterized by their radii. Therefore, outliers need to be eliminated in the following three cases: (i) when the porosity is 0 or greater than 1, (ii) when negative pore sizes result from errors in characterization techniques, and (iii) when negative stress values arise from calibration issues with the stress-strain testing equipment. Additionally, since missing values cannot be directly handled during the machine learning process, they need to be cleared before the model is trained to avoid erroneous training[33].In this study, the "Isnull" function in the Python Pandas library was used to preview the missing values in the dataset, and the previewed data is displayed in Table 1. After previewing the missing values in the dataset, the KNN-Imputer method from the impute module in the Sklearn library was employed to fill the missing values, as demonstrated in Table 2.The missing values in the dataset were estimated using the KNN-Imputer method, which identifies the nearest neighboring values based on the Euclidean distance matrix[34].The theoretical formula for this estimation is provided in Eq. (5).
| $ \begin{aligned} & d(x, y)=\sqrt{\sum\limits_{i=1}^n\left(x_i-y_i\right)^2}= \\ & \quad \sqrt{\left(x_1-x_1\right)^2+\cdots+\left(x_n-x_n\right)^2} \end{aligned} $ | (5) |
| Table 1 KNN-Imputer data preview before processing |
| Table 2 KNN-Imputer previews the processed data |
After data preprocessing, the data samples were divided, with 80% of them being allocated to a training dataset containing 11906 samples, while the remaining 20% were set aside for a testing dataset consisting of 2980 samples.
2.4 Aluminum Foam Feature Selection Model 2.4.1 Naive Bayes classificationThe fundamental principle of the Naive Bayes algorithm for classification is based on the assumption of feature independence. A classification method is constructed using Bayes' theorem, and the information gain metric is employed to quantitatively assess the contribution of each feature to the classification task. Based on the feature contribution scores, the features are ranked by the algorithm to determine which ones are most important for the classification task. Typically, features with higher scores are considered more relevant, and the final feature set is selected based on the top N features with the highest scores.
2.4.2 Random forestAn ensemble learning method called Random Forest, consisting of multiple base decision trees, is employed, as illustrated in Fig. 2. A method for measuring feature importance when assessing feature relevance is offered by this model. During tree construction, metrics are typically utilized to quantify the contribution of each feature to the model's performance, known as Gini importance or MDA (Mean Decrease Accuracy) importance. After training the Random Forest model, importance scores can be obtained for each feature. The top N features with the highest importance scores are selected.

|
Fig.2 Random forest regression principle |
2.4.3 GRNN
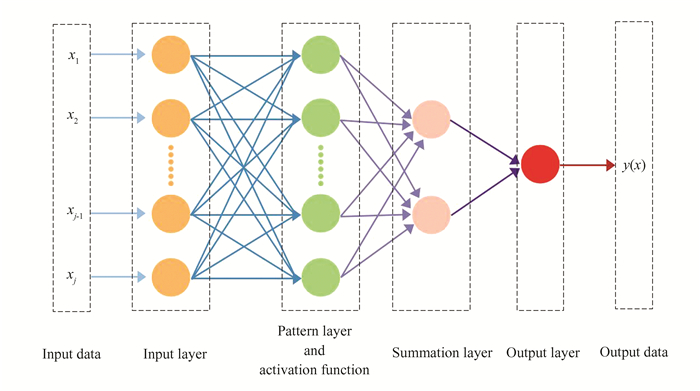
GRNN constructs a neural network for pattern recognition and prediction[35-36]. GRNN comprises four layers: input layer, template layer, product layer, and output layer[37-38]. Fig. 3 illustrates the structure. The input layer takes the feature vector of the input sample and transfers it to the template layer. The template layer includes points in the input feature space associated with each training sample. After it determines the probability distribution for each sample, it passes the information to the product layer. In the product layer, it calculates the distances between the input sample and the templates and uses them as inputs to the radial basis functions, defined by Eq.(6). Finally, it weights and sums the outputs of the product layer in the output layer to obtain the final output result. Eq.(7) provides the basic equation of GRNN.
| $ F(x)=\sum\limits_{i=1}^n \omega_i \phi_i\left(x-C_i\right) $ | (6) |
|
Fig.3 GRNN structure diagram |
In Eq. (6), the output of the input vector x is represented as F(x), and it corresponds to the i-th radial basis function, denoted as ϕi(x-Ci). The weight of the i-th radial basis function is symbolized by ωi, and Ci stands for the center point of this i-th radial basis function[39].
| $ \hat{y}(x)=\hat{f}(x)=\frac{\sum\limits_{i=1}^n y_i K\left(\frac{x-x_i}{h}\right)}{\sum\limits_{i=1}^n K\left(\frac{x-x_i}{h}\right)} $ | (7) |
In Formula (7), the kernel function K() and the smoothing parameter h are used. For interpretation,
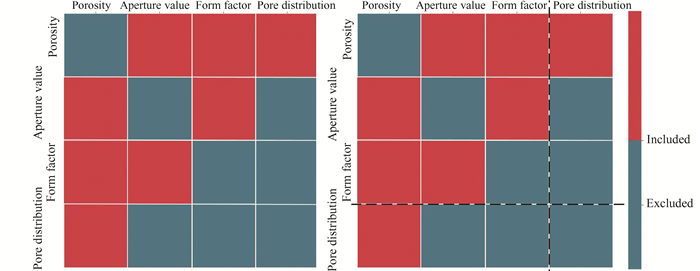
We imported the feature_selection module from the pyGRNN library and assigned it the alias 'FS'. This module encompasses functionality related to feature selection. Subsequently, we instantiated an object named 'IsotropicSelector', which belongs to the Isotropic_selector class within the feature_selection module. This class is specifically designed for isotropic feature selection. To monitor the training time, we used the 'time()' function to record the current timestamp as the starting point. Finally, we invoked the 'relatidness' method of the 'IsotropicSelector' object to conduct feature correlation analysis on the training dataset. The resulting correlation matrix is depicted in Fig. 4. Our analysis focused on inter-feature correlations while excluding the stress-related feature. The outcomes are summarized in Table 3, revealing a higher degree of correlation with porosity and fewer associations with Pore Distribution. Based on this analysis of feature correlations, porosity, aperture, anisotropy, and form factor have been identified as exhibiting the strongest correlations.This analytical approach offers a spatial perspective for examining dependencies and relationships among the dataset's features. Its objective is to comprehend the interactions and associations between the features and their connections with the target variable. This, in turn, enhances our understanding of the dataset's structure and feature interactions, thereby providing valuable insights for subsequent modeling and analysis. Then, the experiment assessed the importance of the other features in the input space when considering the stress feature.
|
Fig.4 Correlation matrix |
| Table 3 KNN-Imputer data preview before processing |
The program used the GridSearchCV algorithm for grid search, automatically selecting the optimal hyperparameters, such as the learning rate, number of iterations, and regularization parameters. Subsequently, we instantiated a GRNN object to implement the GRNN, and we invoked the fit method to train the model using the best bandwidth parameter and optimal model parameters. During the training process, we used a 20-fold cross-validation approach, dividing the dataset into 20 subsets (folds). In each training iteration, 19 subsets were used for training, while one subset was reserved for validation. We repeated this procedure 20 times to ensure that every subset was used for both training and validation. In total, we conducted 7800 model fitting operations. Ultimately, we obtained a subset of features selected through feature selection and compared these selections with the results obtained from random forest and naive Bayes classification, as illustrated in Table 4.
| Table 4 The optimal feature subset chosen by the algorithm |
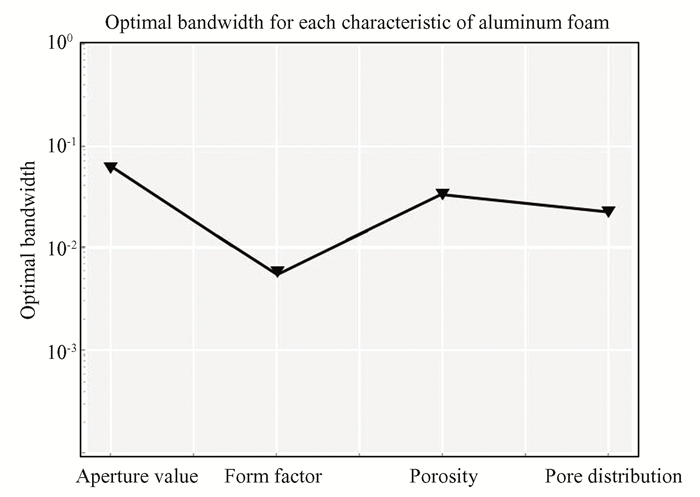
To quantify the correlation between features and compute the similarity between sample points, we introduced an anisotropic Gaussian function[40] as the kernel function for density estimation using the activation function. We obtained the best bandwidth parameter value after training by using the Gaussian kernel function as shown in Fig. 5, and we assigned it to the variable sigma. Eq.(8) provides the expression of the Gaussian kernel function.
| $ K\left(\frac{x-x_i}{h}\right)=\exp \left(\sum\limits_{j=1}^D-\left(\frac{\left(x_j-x_{i j}\right)^2}{2 \sigma_j^2}\right)\right) $ | (8) |
|
Fig.5 Optimum bandwidth parameter |
Here, σj represents the bandwidth of the Gaussian kernel in the JTH dimension.
Table 4 reveals that an accuracy rate of 87.46% is achieved by GRNN. This high accuracy and robustness in classifying the pore characteristics of foam aluminum are exhibited by GRNN. Various types of data and noise can be handled by it, resulting in reduced susceptibility to outliers or noise in the data. This suggests that even in the presence of anomalies in real-world datasets, relatively stable performance can be maintained by GRNN. Furthermore, an impressive AUC-ROC score of 0.92 is achieved, indicating that strong performance is maintained by the GRNN model across different true positive rates and false positive rates when the classification threshold is adjusted. The high AUC-ROC score of 0.92 also implies that erroneous positive predictions are effectively reduced by the GRNN model, thereby decreasing the misclassification rate of the model. Additionally, formidable nonlinear modeling capabilities are possessed by GRNN, enabling the automatic learning and selection of the most relevant features during the training process. This implies that the features most critical to model performance can be better identified by it, mitigating potential subjective bias that might be introduced when features are manually selected. In contrast, the random forest model achieves an accuracy of 79.25% and an AUC-ROC of 0.88, demonstrating good performance but slight inferiority to GRNN. Relative to the other two models, Naive Bayes exhibits an accuracy of 71.64% and an AUC-ROC of 0.81, indicating lower performance.
When considering both accuracy and AUC-ROC values, the choice of GRNN as the optimal feature selection model is made due to its higher accuracy, superior positive and negative class classification performance, enhanced model robustness and adaptability, and lower misclassification rate.
The optimal bandwidth plays a crucial role in both key feature selection and the enhancement of model performance. It significantly impacts the allocation of feature weights in machine learning models such as GRNN. The bandwidth determines the degree of contribution of each feature to the model, with a larger bandwidth resulting in a more uniform weight distribution, while a smaller bandwidth emphasizes local features among samples. Therefore, selecting an appropriate bandwidth helps identify which features are most critical to the model's performance. Furthermore, the bandwidth can influence the measurement of correlations between features. A larger bandwidth may reduce inter-feature correlations by considering a broader neighborhood, whereas a smaller bandwidth may focus more on local features, increasing the correlations between features. Optimal bandwidth selection allows for better capture of inter-feature correlations, aiding in the selection of key features. On the other hand, finding the right bandwidth can balance the importance of features within the training data, thereby improving the model's generalization ability and mitigating overfitting issues caused by the model's sensitivity to noisy data. When the model is less perturbed by minor variations in input data, it greatly enhances its stability. Based on the accuracy of the model's stability in feature selection, we chose to utilize the feature selection results and feature importance coefficients obtained from the GRNN, as shown in Table 5.
| Table 5 The importance coefficient of the selected feature |
3 Equivalent Porosity Formula 3.1 Establishment of Equivalent Porosity Formula
The establishment of the equivalent porosity formula relies on us comprehensively considering the contribution of each important feature to stress and transforming the characterization problem into a numerical indicator. This approach enables us to better understand and describe complex datasets, offering intuitive and concise information to support decision-making and analysis of foam aluminum's mechanical performance. In this experiment, we drew inspiration from machine learning and combined the weighted sum of feature weights[41] with the allocation of residual weights to comprehensively assess the importance of each feature. Specifically, we summed the feature weights and the allocated residual weights, multiplied the values of each feature by their corresponding weights, and calculated the sum of the weighted values of all features. This yielded a comprehensive feature evaluation value that described the mechanical performance of foam aluminum. Next, we formalized this comprehensive value into a feature evaluation formula, converting the comprehensive feature evaluation value into a feature evaluation equation. Through the establishment of the feature evaluation formula for equivalent porosity, we integrated multiple important features into a comprehensive indicator, simplifying complex datasets for easier interpretation and application. Such a feature evaluation formula provides an intuitive and comparable reference for analyzing and making decisions about the mechanical performance of foam aluminum. By weighing the contributions of different features, we can comprehensively assess the performance of foam aluminum and provide a more accurate and reliable data foundation for material research.
However, determining the weight values of features poses a complex and challenging task, as it requires evaluating their importance, influence, and contribution. At present, several mainstream methods exist for accurately determining weight values:
1) Domain knowledge and expert judgment: This method may rely on the experience and judgment of domain experts.
2) Statistical methods[42]: Statistical methods are used to measure the correlation between features and the target variable, requiring the establishment of the relationship strength between features and the target variable.
3) Feature selection based on optimization algorithms[43].
4) Feature selection based on information theory[44].
In this experiment, our analysis is based on the GRNN model to assess feature importance and generate indicators of feature significance through machine learning. These indicators can gauge each feature's contribution to the model's performance. Through an analysis of feature importance in the model and the acquisition of weight values, we assign appropriate weights to the original features. As the sum of feature weights obtained from the GRNN learning algorithm is less than 1, we distribute the remaining weights among each feature to maintain their proportional relationship. If the sum of the original feature weights is less than 1 and the number of features is N, the residual weight is 1-ω. Then the assigned residual weight for each feature is (1-ω)/N. The method of allocating the residual weight is to divide the residual weight by the number of features, and then add the resulting result to each feature weight.Assuming the original feature weights are denoted as ω1, ω2, ..., ωn and the remaining weights as
The available surplus weight for distribution is
| $ \begin{aligned} R= & 1-\left(\omega_{\text {Porosity }}+\omega_{\text {Aperture }}+\omega_{\text {Form Factor }}+\omega_{\text {Anisotropy }}\right)= \\ & 0.2853154 \end{aligned} $ |
Then, according to the allocation formula, the surplus weight is evenly distributed among each feature weight.
The new feature weights
| $ \begin{gathered} \omega_{\text {Porosity }}^{\prime}=0.69912, \omega_{\text {Aperture }}^{\prime}=0.12342 \\ \omega_{\text {FormFactor }}^{\prime}=0.08372, \omega_{\text {Ay }}^{\prime}=0.09374 \end{gathered} $ |
We use the weights from the feature evaluation formula to weight and sum the features, resulting in a new representation index called the Wang Equivalent Porosity (WEP). This index provides a better representation of the target variable. The formula for WEP is given by Eq.(9).
| $ \begin{array}{r} \text { WEP }=\left\{100-\left[P \left(\omega_{\mathrm{p}}+\left(1-\left(\omega_{\mathrm{p}}+\omega_{\mathrm{A}}+\omega_{\mathrm{F}}+\right.\right.\right.\right.\right. \\ \left.\left.\left.\omega_{\mathrm{Ay}}\right)\right) / N\right)+A\left(\omega_{\mathrm{A}}+\left(1-\left(\omega_{\mathrm{p}}+\omega_{\mathrm{A}}+\left(\omega_{\mathrm{F}}+\right.\right.\right.\right. \end{array} \\ \begin{aligned} & \left.\left.\left.\omega_{\text {Ay }}\right)\right) / N\right)+F\left(\omega_{\mathrm{F}}+\left(1-\left(\omega_{\mathrm{p}}+\omega_{\mathrm{A}}+\left(\omega_{\mathrm{F}}+\right.\right.\right.\right. \\ & \left.\left.\left.\omega_{\mathrm{Ay}}\right)\right) / N\right)+\operatorname{Ay}\left(\omega_{\mathrm{Ay}}+\left(1-\left(\omega_{\mathrm{p}}+\omega_{\mathrm{A}}+\left(\omega_{\mathrm{F}}+\right.\right.\right.\right. \\ & \left.\left.\left.\left.\left.\omega_{\mathrm{Ay}}\right)\right) / N\right)\right]\right\} / 100 \times 100 \% \end{aligned} $ | (9) |
here, WEP is equivalent porosity, ωP is the quantitative weight value of the contribution degree of porosity to the compressive stress of aluminum foam, which is 0.62779; ωA is the quantitative weight value of the contribution degree of aperture to compressive stress of aluminum foam, which is 0.052087;ωF is the quantitative weight value of the contribution degree of the shape factor to the compressive stress of aluminum foam, which is 0.012393; ωAy is the quantitative weight value of the contribution of anisotropy to the compressive stress of aluminum foam, which is 0.0224146; P is the porosity of aluminum foam, the value specification is ζ%×100, A is the average pore diameter of aluminum foam pores, and the value specification is mm. F is the shape factor of the aluminum foam pores, and the value range is (0, 1).Ay is the anisotropy of the pore.
The simplified formula:
| $ \begin{gathered} \omega_{\mathrm{P}}^{\prime}=\omega_{\mathrm{P}}+\frac{1-\left(\omega_{\mathrm{P}}+\omega_{\mathrm{A}}+\omega_{\mathrm{F}}+\omega_{\mathrm{Ay}}\right)}{N} \\ \omega_{\mathrm{A}}^{\prime}=\omega_{\mathrm{A}}+\frac{1-\left(\omega_{\mathrm{P}}+\omega_{\mathrm{A}}+\omega_{\mathrm{F}}+\omega_{\mathrm{Ay}}\right)}{N} \\ \omega_{\mathrm{F}}^{\prime}=\omega_{\mathrm{F}}+\frac{1-\left(\omega_{\mathrm{P}}+\omega_{\mathrm{A}}+\omega_{\mathrm{F}}+\omega_{\mathrm{Ay}}\right)}{N} \\ \omega_{\mathrm{Ay}}^{\prime}=\omega_{\mathrm{F}}+\frac{1-\left(\omega_{\mathrm{P}}+\omega_{\mathrm{A}}+\omega_{\mathrm{F}}+\omega_{\mathrm{Ay}}\right)}{N} \\ R=1-\left(\omega_{\mathrm{P}}+\omega_{\mathrm{A}}+\omega_{\mathrm{F}}+\omega_{\mathrm{Ay}}\right) \end{gathered} $ |
| $ \begin{aligned} \mathrm{WEP} & =\left\{100-\left[P\left(\omega_{\mathrm{p}}+R / N\right)+A\left(\omega_{\mathrm{A}}+R / N\right)+\right.\right. \\ & \left.\left.F\left(\omega_{\mathrm{F}}+R / N\right)+\operatorname{Ay}\left(\omega_{\mathrm{Ay}}+R / N\right)\right]\right\} / 100 \times \\ & 100 \% \end{aligned} $ |
| $ \begin{aligned} \mathrm{WEP}= & \left\{100-\left[P \omega_{\mathrm{P}}^{\prime}+A \omega_{\mathrm{A}}^{\prime}+F \omega_{\mathrm{F}}^{\prime}+\right.\right. \\ & \left.\left. \text{Ay} \omega_{\mathrm{Ay}}^{\prime}\right]\right\} / 100 \times 100 \% \end{aligned} $ |
where, WEP is equivalent porosity, ω'P is the weight value of the secondary distribution of the porosity contribution degree to the compressive stress of aluminum foam, which is 0.69912.ω'A is the weight value of the secondary distribution of the contribution degree of aperture to compressive stress of aluminum foam, which is 0.12342.ω'F is the secondary distribution weight value of the contribution degree of the shape factor to the compressive stress of aluminum foam, which is 0.08372.ω'Ay is whether the weight value of the quadratic distribution of the contribution degree of anisotropy to the compressive stress of aluminum foam is 0.09374.
3.2 Verification of Equivalent Porosity FormulaWe conducted a secondary verification using the WEP formula, based on the preparation and characterization of foam aluminum by researchers such as Tang from Southeast University [45], Zhou from Taiyuan University of Technology [46], Sun from Beijing General Research Institute of Nonferrous Metals[47], and Hangai from Gunma University in Japan[48], along with the static compression test results on foam aluminum specimens. The verification results are presented in Table 6.
| Table 6 The verification results |
We employed 11 sets of samples from four different research institutions with variations in porosity, pore size, and pore circularity to validate the proposed formula. In parallel, the results of the Gibson-Ashby formula were used as a comparative benchmark. Fig. 6 illustrates the variations in WEP concerning stress for foam aluminum. The comparative outcomes indicate that as platform stress during quasi-static compression of foam aluminum samples increased, the WEP values calculated based on feature data also increased. For instance, when sample 3 experienced a stress level of 5.32 MPa, the corresponding equivalent porosity was 35.55%. Similarly, for sample MF77, with a stress value of 10.4 MPa, the equivalent porosity reached 43.42%. Among the 11 datasets, clear outliers were observed in the results generated by the Gibson-Ashby formula in two cases, specifically at Gunma University Japan and Beijing General Research Institute of Nonferrous Metals. In contrast, the evaluation results using WEP consistently demonstrated outstanding accuracy without any outliers. Relative to the traditional Gibson-Ashby formula, WEP enhanced the accuracy of mechanical performance evaluation for foam aluminum by 18.18%. This improvement value clearly emphasizes the superior performance of the newly proposed formula in mechanical performance assessment, providing a more reliable and accurate tool for assessing the performance of foam aluminum and other porous materials.

|
Fig.6 Comparison of WEP and stress variation trends |
In summary, the validation of 11 datasets confirms the accuracy and reliability of the proposed formula, affirming its ability to comprehensively consider multiple features and offer a comprehensive assessment of the mechanical performance characteristics of foam aluminum. Thus, this formula establishes a foundation for more precise predictions and analyses.
4 Comparison of Equivalent Porosity with Gibson-Ashby FormulaThe Gibson-Ashby formula is an empirical equation proposed by Gibson and Ashby that estimates the relationship between the mechanical properties of porous materials and their porosity[49]. Eq.(9) displays the formula:
| $ \sigma_f=\sigma_{\mathrm{c}} \cdot\left(\frac{1-\rho}{\rho_{\mathrm{c}}}\right)^n $ | (10) |
where σf is the strength of the porous material, σc is the strength of the non-porous version of the same material, ρ is the porosity, ρc is the critical porosity, and n is the material specific constant.
While researchers can find useful estimates using the Gibson-Ashby formula in certain scenarios, it also demonstrates several drawbacks and limitations. Firstly, researchers derive the formula based on empirical data and fitted parameters, which constrains its applicability to the choice of the dataset and parameter selection. As a result, the model may lack accuracy or generality in specific situations. Secondly, researchers rely on several simplifying assumptions when using the formula, such as isotropic pore structures and uniform stress distributions. However, these assumptions may not hold for certain foam metal materials, particularly under non-uniform or complex stress conditions. Furthermore, the formula does not consider variations in pore characteristics and how they affect mechanical performance. Gibson-Ashby formula typically assumes that pores are spherical or approximately spherical, whereas actual pore shapes in foam materials can be more complex. Finally, researchers should note that the pore structure of aluminum foam significantly influences its macroscopic properties, particularly under high-stress and strain conditions. Yet, the Gibson-Ashby formula does not incorporate these factors related to the pore structure of foam metals into its modeling. In summary, although researchers can gain valuable insights from the Gibson-Ashby formula, it possesses limitations arising from its empirical nature, simplifying assumptions, and neglect of variations in pore structure. Researchers and practitioners should exercise caution and consider these limitations when applying the formula, especially in cases where foam metal materials exhibit non-standard behaviors or complex pore structures.
Researchers base the Gibson-Ashby formula on the assumption that the strength of a material depends on its porosity. They observe that as porosity increases, the material's strength decreases. They adjust this relationship using the exponent 'n' in the formula, where a higher 'n' value signifies a more sensitive impact of porosity on strength, while a lower 'n' value signifies a lesser impact[50].In comparison to the Gibson-Ashby formula, researchers find that the new characterization formula offers significant advantages in terms of comprehensive performance description, data-driven modeling, interpretability, and flexibility. Let's delve into a more detailed description of these advantages:
1) Comprehensive performance description: Researchers consider the weights of multiple characterization indicators in the new characterization formula and account for their importance, resulting in a more comprehensive description of foam aluminum's performance characteristics. In contrast, the Gibson-Ashby formula relies solely on porosity as a single indicator to describe foam aluminum's performance. Researchers can more accurately reveal foam aluminum's performance characteristics and provide more precise predictions and evaluations through the new characterization formula.
2) Data-driven modeling: Researchers build the new characterization formula using machine learning methods, utilizing structural characterization data and mechanical performance data of foam aluminum for model training. In contrast, researchers derive the Gibson-Ashby formula based on empirical relationships between porosity and material performance[28]. Machine learning methods can learn more complex patterns and relationships from a large amount of data, providing researchers with more accurate and reliable predictive capabilities.
3) Interpretability and flexibility: Researchers find that the new characterization formula, based on machine learning methods, offers a certain level of interpretability. By analyzing the model, the importance of each characterization indicator in foam aluminum performance can be understood, further deepening the understanding of the performance mechanisms of foam aluminum.
Additionally, researchers can adjust and optimize the contribution of each feature according to specific needs through weight allocation and secondary allocation in the new characterization formula. This flexibility enables the new characterization formula to be adjusted and optimized based on practical requirements, adapting to the demands of different application scenarios.
The application of the WEP formula is of paramount significance in designing and industrially applying high-performance aluminum foam.
1) Performance optimization: Designers can make targeted improvements or optimizations to specific features by gaining a clear understanding of which features have the most significant impact on the performance of aluminum foam. This aids in enhancing the performance of aluminum foam for specific applications, meeting the diverse demands of various industries.
2) In accordance with the practice of writing English academic papers, change the following English quotes to the active voice (the subject is the person or thing performing the action (i.e. the speaker)) and use the passive voice (the person performing the action is unclear or unimportant). The passive voice puts the focus on the recipient or object of the action rather than the performer.
3) Customized products: Leveraging the WEP formula allows for the customization of high-performance aluminum foam to meet the specific demands of particular sectors, such as automotive manufacturing, construction, aerospace, and others, which have unique requirements for the performance of aluminum foam.
4) Quality control: Regular inspections of WEP values, facilitated by the WEP formula, enable the timely detection of potential issues, providing an objective assessment standard that can be employed to monitor the quality and performance of aluminum foam. This, in turn, allows for corrective measures to enhance the production process.
In summary, the WEP formula provides a scientific foundation for designers and manufacturers to gain a deeper understanding of aluminum foam's performance characteristics. It also enables them to have better control over its properties, thus driving its widespread utilization across various industries in the design and industrial application of high-performance aluminum foam.
5 ConclusionsIn this study, we adopt an interdisciplinary approach by combining materials science with machine learning. Machine learning techniques, such as feature selection, feature weight analysis, and residual weight allocation, are integrated to establish a formula for equivalent porosity. We have demonstrated the accuracy of equivalent porosity as a new characterization parameter through the validation of five sample sets, providing a precise reflection of foam aluminum's performance. We provide a more precise method for evaluating and analyzing the material's mechanical properties, offering valuable references for decision-making and analysis. The research closely aligns with the rapid advancements in big data and artificial intelligence technologies by merging data-driven materials research with the study of foam aluminum. We introduce novel patterns and methods, offering a fresh perspective on the characterization and analysis of foam aluminum's performance.
However, certain limitations within the current work need to be acknowledged. First, the machine learning model's feature weight weighting method does not allow dynamic adjustments of feature weights, which restricts the model's adaptability and flexibility in different scenarios. Second, although we introduced the residual weight allocation method in this study, further research is needed to refine the weight allocation strategy to consider different types and sources of residuals. This will require more complex models and algorithms to better simulate and predict the impact of residual terms.
In future research, we may expand the scope of sample validation to include a broader range of foam aluminum types and characteristics, further confirming the universality of equivalent porosity as a performance parameter. Additionally, future research can explore and integrate additional features to construct a more comprehensive model, which may necessitate more extensive data collection and feature engineering efforts.
Lastly, beyond mechanical performance, future studies may consider introducing other performance parameters to provide a more holistic description of foam aluminum's properties and applications.
| [1] |
Bangash M K, Ubertalli G, Di Saverio D, et al. Joining of aluminium alloy sheets to aluminium alloy foam using metal glasses. Metals, 2018, 8(8): 614. DOI:10.3390/met8080614 (  0) 0) |
| [2] |
Wan T, Liu Y, Zhou C, et al. Fabrication, properties, and applications of open-cell aluminum foams: a review. Journal of Materials Science & Technology, 2021, 62: 11-24. DOI:10.1016/j.jmst.2020.05.039 (  0) 0) |
| [3] |
Miyoshi T, Itoh M, Akiyama S, et al. ALPORAS aluminum foam: production process, properties, and applications. Advanced Engineering Materials, 2000, 2(4): 179-183. DOI:10.1002/(SICI)1527-2648(200004)2:4<179::AID-ADEM179>3.0.CO;2-G (  0) 0) |
| [4] |
Gibson L J, Ashby M F. Cellular Solids: Structure and Properties. 2nd ed. Cambridge: Cambridge University Press, 1997.
(  0) 0) |
| [5] |
Hanssen A G, Hopperstad O S, Langseth M, et al. Validation of constitutive models applicable to aluminium foams. International Journal of Mechanical Sciences, 2002, 44(2): 359-406. DOI:10.1016/S0020-7403(01)00091-1 (  0) 0) |
| [6] |
Vengatachalam B, Poh L, Liu Z, et al. Three dimensional modelling of closed-cell aluminium foams with predictive macroscopic behaviour. Mechanics of Materials, 2019, 136: 103067. DOI:10.1016/j.mechmat.2019.103067 (  0) 0) |
| [7] |
Shi X P, Liu S Y, Nie H L, et al. Study of cell irregularity effects on the compression of closed-cell foams. International Journal of Mechanical Sciences, 2018, 135: 215-225. DOI:10.1016/j.ijmecsci.2017.11.026 (  0) 0) |
| [8] |
Xi C Q, Li Q M. Meso-scale mechanism of compaction shock propagation in cellular materials. International Journal of Impact Engineering, 2017, 109: 321-334. DOI:10.1016/j.ijimpeng.2017.07.005 (  0) 0) |
| [9] |
Farabet C, Couprie C, Najaman L, et al. Learning hierarchical features for scene labeling. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1915-1929. DOI:10.1109/TPAMI.2012.231 (  0) 0) |
| [10] |
Szegedy C, Liu W, Jia Y Q, et al. Going deeper with convolutions. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2015: 1-9. DOI: 10.1109/CVPR.2015.7298594.
(  0) 0) |
| [11] |
Helmstaedter M, Briggman K L, Turaga S C, et al. Connectomic reconstruction of the inner plexiform layer in the mouse retina. Nature, 2013, 500(7461): 168. DOI:10.1038/nature12346 (  0) 0) |
| [12] |
Jamshidi-Alashti R, Mohammadi Zahrani M, Niroumand B. Use of artificial neural networks to predict the properties of replicated open-cell aluminum alloy foam via processing parameters of melt squeezing procedure. Materials & Design, 2013, 51: 1035-1044. DOI:10.1016/j.matdes.2013.05.026 (  0) 0) |
| [13] |
Fatriansyah J F, Suhariadi I, Fauziyyah H A, et al. Prediction and optimization of mechanical properties of Ni based and Fe-Ni based super alloys via neural network approach with alloying composition parameter. Journal of Materials Research and Technology, 2023, 24: 4168-4176. DOI:10.1016/j.jmrt.2023.04.065 (  0) 0) |
| [14] |
Romano M, Contu G, Mola F, et al. Threshold-based naïve Bayes classifier. Advances in Data Analysis and Classification, 2023, 18: 325-361. DOI:10.1007/s11634-023-00536-8 (  0) 0) |
| [15] |
Ratnasingam S, Muñoz-Lopez J. Distance correlation-based feature selection in random forest. Entropy, 2023, 25(9): 1250. DOI:10.3390/e25091250 (  0) 0) |
| [16] |
Niu D, Wang H, Chen H, et al. The general regression neural network based on the fruit fly optimization algorithm and the data inconsistency rate for transmission line icing prediction. Energies, 2017, 10(12): 2066. DOI:10.3390/en10122066 (  0) 0) |
| [17] |
Li K, Wang F, Yang L, et al. Deep feature screening: Feature selection for ultra high-dimensional data via deep neural networks. Neurocomputing, 2023, 538: 126186. DOI:10.1016/j.neucom.2023.03.047 (  0) 0) |
| [18] |
Wang L, Ma X, Zhang J. Feature screening for ultrahigh-dimensional additive logistic models. Journal of Statistical Planning and Inference, 2020, 205: 306-317. DOI:10.1016/j.jspi.2019.08.005 (  0) 0) |
| [19] |
Ramirez-Gonzalez M, Sevilla F R S, Korba P, et al. Convolutional neural nets with hyperparameter optimization and feature importance for power system static security assessment. Electric Power Systems Research, 2022, 211: 108203. DOI:10.1016/j.epsr.2022.108203 (  0) 0) |
| [20] |
Garg M, Goel A. Preserving integrity in online assessment using feature engineering and machine learning. Expert Systems with Applications, 2023, 225: 120111. DOI:10.1016/j.eswa.2023.120111 (  0) 0) |
| [21] |
Saravanakumar A, Rajeshkumar L, Balaji D, et al. Prediction of wear characteristics of AA2219-Gr matrix composites using GRNN and Taguchi-Based approach. Arabian Journal for Science and Engineering, 2020, 45: 9549-9557. DOI:10.1007/s13369-020-04817-8 (  0) 0) |
| [22] |
Li X, Liu M, Wang K, et al. Data cleaning method for the process of acid production with flue gas based on improved random forest. Chinese Journal of Chemical Engineering, 2023, 59: 72-84. DOI:10.1016/j.cjche.2022.12.013 (  0) 0) |
| [23] |
Ji C, Huang H, Wang T, et al. Recent advances and future trends in processing methods and characterization technologies of aluminum foam composite structures: A review. Journal of Manufacturing Processes, 2023, 93: 116-152. DOI:10.1016/j.jmapro.2023.03.015 (  0) 0) |
| [24] |
Zhou X, Li Y, Chen X. Development of AlMg35-TiH2 composite foaming agent and fabrication of small pore size aluminium foams. Journal of Materials Processing Technology, 2020, 283: 116698. DOI:10.1016/j.jmatprotec.2020.116698 (  0) 0) |
| [25] |
Huang Z, Hu C, Shen L, et al. Preparation and characterization of light weight aluminum matrix syntactic foams with high energy absorbing capacity. Materials Science and Engineering: A, 2023, 872: 144942. DOI:10.1016/j.msea.2023.144942 (  0) 0) |
| [26] |
Huluka S, Abdul-Latif A, Baleh R, et al. Biaxial characterization of open-cell aluminum foams from macro to micro responses. Materials Science and Engineering: A, 2023, 868: 144588. DOI:10.1016/j.msea.2023.144588 (  0) 0) |
| [27] |
Vengatachalam B, Huang R, Poh L H, et al. Initial yield behaviour of closed-cell aluminium foams in biaxial loading. International Journal of Mechanical Sciences, 2021, 191: 106063. DOI:10.1016/j.ijmecsci.2020.106063 (  0) 0) |
| [28] |
Zhao W, He S, Wei X, et al. Quantitative relationships between cellular structure parameters and the elastic modulus of aluminum foam. Materials Science and Engineering: A, 2023, 868: 144713. DOI:10.1016/j.msea.2023.144713 (  0) 0) |
| [29] |
Li D-W, Li J, Li T, et al. Preparation and characterization of aluminum foams with ZrH2 as foaming agent. Transactions of Nonferrous Metals Society of China, 2011, 21(2): 346-352. DOI:10.1016/S1003-6326(11)60720-6 (  0) 0) |
| [30] |
hulasikanth V, Padmanabhan R. Processing and testing of closed cell aluminium hybrid composite foams. Materials Today: Proceedings, 2021, 46(2): 1437-1440. DOI:10.1016/j.matpr.2021.03.017 (  0) 0) |
| [31] |
harkaluk E, Constantinescu A, Szmytka F, et al. Probability density functions: From porosities to fatigue lifetime. International Journal of Fatigue, 2014, 63: 127-136. DOI:10.1016/j.ijfatigue.2014.01.017 (  0) 0) |
| [32] |
Hassanli F, Paydar M H. Improvement in energy absorption properties of aluminum foams by designing pore-density distribution. Journal of Materials Research and Technology, 2021, 14: 609-619. DOI:10.1016/j.jmrt.2021.06.073 (  0) 0) |
| [33] |
Wang H, Zhou X-Y, Long B, et al. Thermal properties of closed-cell aluminum foams prepared by melt foaming technology. Transactions of Nonferrous Metals Society of China, 2016, 26(12): 3147-3153. DOI:10.1016/S1003-6326(16)64446-1 (  0) 0) |
| [34] |
Mirzaali M J, Libonati F, Vena P, et al. Investigation of the effect of internal pores distribution on the elastic properties of closed-cell aluminum foam: A comparison with cancellous bone. Procedia Structural Integrity, 2016, 2: 1285-1294. DOI:10.1016/j.prostr.2016.06.164 (  0) 0) |
| [35] |
Specht D F. A general regression neural network. IEEE Transactions on Neural Networks, 1991, 2(6): 568-576. DOI:10.1109/72.97934 (  0) 0) |
| [36] |
Xia C, Lei B, Wang H, et al. GRNN short-term load forecasting model and virtual instrument design. Energy Procedia, 2011, 13: 9150-9158. DOI:10.1016/S1876-6102(14)00454-8 (  0) 0) |
| [37] |
Aengchuan P, Wiangkham A, Klinkaew N, et al. Prediction of the influence of castor oil-ethanol-diesel blends on single-cylinder diesel engine characteristics using generalized regression neural networks (GRNNs). Energy Reports, 2022, 8(3): 38-47. DOI:10.1016/j.egyr.2022.10.113 (  0) 0) |
| [38] |
Iban M C, Şentürk E. Machine learning regression models for prediction of multiple ionospheric parameters. Advances in Space Research, 2022, 69(3): 1319-1334. DOI:10.1016/j.asr.2021.11.026 (  0) 0) |
| [39] |
Mokari E, Mohebzadeh H, Samani Z, et al. Spatiotemporal imputation of MODIS land surface temperature using machine learning techniques (Case study: New Mexico's Lower Rio Grande Valley). Remote Sensing Applications: Society and Environment, 2021, 24: 100651. DOI:10.1016/j.rsase.2021.100651 (  0) 0) |
| [40] |
Su R, Sun C, Zhang C, et al. A new method for linear feature and junction enhancement in 2D images based on morphological operation, oriented anisotropic Gaussian function and Hessian information. Pattern Recognition, 2014, 47(10): 3193-3208. DOI:10.1016/j.patcog.2014.04.024 (  0) 0) |
| [41] |
Luong A V, Nguyen T T, Han K, et al. DEFEG: Deep ensemble with weighted feature generation. Knowledge-Based Systems, 2023, 275: 110691. DOI:10.1016/j.knosys.2023.110691 (  0) 0) |
| [42] |
Martin N, Yang C. Statistical learning of water budget outcomes accounting for target and feature uncertainty. Journal of Hydrology, 2023, 624: 129946. DOI:10.1016/j.jhydrol.2023.129946 (  0) 0) |
| [43] |
Zhuang Z, Pan J-S, Li J, et al. Parallel binary arithmetic optimization algorithm and its application for feature selection. Knowledge-Based Systems, 2023, 275: 110640. DOI:10.1016/j.knosys.2023.110640 (  0) 0) |
| [44] |
Tiwari A, Chaturvedi A. A hybrid feature selection approach based on information theory and dynamic butterfly optimization algorithm for data classification. Expert Systems with Applications, 2022, 196: 116621. DOI:10.1016/j.eswa.2022.116621 (  0) 0) |
| [45] |
Tang G. Mechanical Properties Analysis of Closed Cell Aluminum Foam based on Porous Structure Parameters. Jiangsu: Southeast University, 2021.
(  0) 0) |
| [46] |
Zhou X. Preparation of Aluminum Foam by Melt Foaming Method and Optimization of Pore Structure. Shanxi: Taiyuan University of Science and Technology, 2023.
(  0) 0) |
| [47] |
Sun Q. Study on Preparation, Characterization and Properties of Aluminum Alloy Foam by Powder Metallurgy. Beijing: Beijing General Research Institute of Nonferrous Metals, 2016.
(  0) 0) |
| [48] |
Hangai Y, Kato H, Utsunomiya T, et al. Effects of porosity and pore structure on compression properties of blowing-agent-free aluminum foams fabricated from aluminum alloy die castings. Materials Transactions, 2012, 53(8): 1515-1520. DOI:10.2320/matertrans.M2012125 (  0) 0) |
| [49] |
Kornievsky A, Nasedkin A. Numerical investigation of mechanical properties of foams modeled by regular Gibson-Ashby lattices with different internal structures. Materialia, 2022, 26: 101563. DOI:10.1016/j.mtla.2022.101563 (  0) 0) |
| [50] |
Jelitto H, Schneider G A. Extended cubic fracture model for porous materials and the dependence of the fracture toughness on the pore size. Materialia, 2020, 12: 100761. DOI:10.1016/j.mtla.2020.100761 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


