2. Chengdu Hangli (Group) Industrial Co., Ltd, Chengdu 611937, China
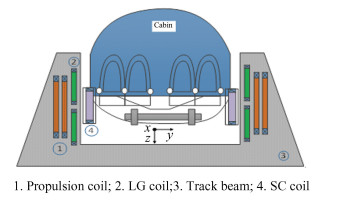
High-speed maglev systems has become a highly competitive new green ground transportation tool in urban rail transit[1-4]. At present, relatively mature maglev train technologies include EMS (Electro Magnetic Suspension) and EDS (Electro Dynamic Suspension), in which EMS levitation/guidance adopts active control, and the levitation gap is only one-tenth that of EDS. Therefore, accurate levitation and guidance control play crucial roles in the operation of an EMS. The concept of electrodynamics was proposed by Powell and Danby[1] of American scientists in 1966, and then Japan, the United States, South Korea, and China began to develop electric maglev technology. Japan introduced this technology in the 1970s and conducted both theoretical and experimental research. The construction of Japan's maglev Central Shinkansen, with a maximum speed of 500 km/h, started to operate at the end of 2014. The section from Pingchuan to Nagoya in Tokyo is expected to operate in 2027.The levitation air gap of EDS is 100 mm without a complex control system. Therefore, EDS is an ideal vehicle with ultra-high speed [5-6]. Therefore, this study considers a superconducting electrodynamic maglev train of MLX01 type as the research object. A diagram of MLX01 type is shown in Fig. 1 and the parameters of the coil are listed in Ref.[7]. When the train is in the track center, the distance in the y-direction between the center of the SC (Superconducting) coil and LG (Levitation and Guidance) coil is standard air gap (Sag). Because the levitation and guidance of maglev trains adopt the principle of electromagnetic induction, the electromagnetic damping force between the vehicle and track is small during train operation[8-9]. Therefore, it is of great significance to reveal damping characteristics and increase electromagnetic damping force.
|
Fig.1 The cross section of superconducting electrodynamic maglev train of MLX01 type |
He et al.[10] transformed the electromagnetic relationship between the SC and LG coils into an equivalent circuit model and solved the force of the train by using the energy method. Yonezu and other scholars[11-12] studied the electromagnetic force on the bogie and improved the superconducting electrodynamic maglev system. Watanabe and other scholars[13] considered a four-degree-of-freedom dynamic model and studied the dynamic characteristics of a vehicle body and a bogie. Because high-speed maglev trains are subject to complex environmental disturbances during train operation, which have an important impact on the stability of trains, therefore, scholars have designed and adopted different stability control strategy and algorithms to improve the stability performance of maglev trains[14-17]. Scholars have conducted extensive research on EDS and achieved good research results, but they have not established the electromagnetic coupling model of a single bogie, resulting in errors in the calculation results. The variation rule of the electromagnetic spring coefficient of a bogie is not deeply analyzed. The vibration characteristics of the bogie under different electromagnetic damping strategies is not thoroughly compared and analyzed. When evaluating the dynamic characteristics of the superconducting electrodynamic maglev train, the degree of freedom of superconducting electrodynamic maglev train is relative few.
To solve the above-mentioned research deficiencies, the same coupling numerical model of a single bogie as used in the previous study[18-19] was adopted. The variation rule of the electromagnetic spring coefficient of a bogie was analyzed. A passive damping control strategy and an active damping control strategy were designed to increase the electromagnetic damping of superconducting electrodynamic maglev train and realize stable operation of the train. Combined with the numerical model of a single bogie, the vibration rule of the bogie in different directions with different damping control strategies was studied. The research results can provide a theoretical foundation for resisting external disturbances and evaluating the stable operation of superconducting electrodynamic maglev train.
1 Characteristics of Electromagnetic Spring of Superconducting Electrodynamic Maglev TrainThe levitation and guidance functions were realized through a combination with the SC coil. In previous studies, the field-circuit-motion coupling model of a single bogie was established in Ref.[14] and the force on a single bogie of the Yamanashi Maglev Test train were measured in Ref.[20]. The forces of the superconducting electrodynamic maglev train at different speeds are shown in Fig. 2. The simulation data are consistent with the measured data of the Yamanashi test line[20], which verifies the correctness of the field-circuit-motion coupling model. The reason for the errors between the calculated values and the measured values has been studied in the previous rearch[18-19].

|
Fig.2 Relationship between velocity and force of on one side of a bogie |
It can be seen from Fig. 2 that when the speed of the superconducting electrodynamic maglev train is less than 120 km/h, the LG coil cannot provide sufficient levitation and guidance force, which can not maintain stable levitation and guidance of the superconducting electrodynamic maglev train. Therefore, the train operates with the assistance of the supporting wheels installed on the bogie. It is defined that the distance in the z-direction between the SC coil center and LG coil center is levitation displacement. When the train deviates from the track center, the difference between Sag and the distance between the SC and LG coils in the y-direction is the guide displacement. When a bogie has a small offset, an electromagnetic spring coefficient is used to replace the electromagnetic force on the bogie. When the weight supported by the bogie is equal to the levitation force provided by the LG coil, the levitation displacement at this time is called a balanced displacement.
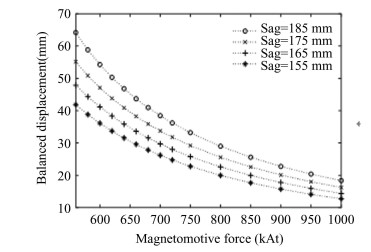
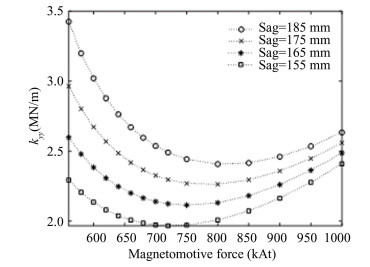
Based on the field-circuit-motion coupling numerical model of a single bogie, the characteristics of levitation balance displacement under different Sags and MFs when v= 600 km/h are shown in Fig. 3. When Sag decreases or MF increases, the magnetic flux between the SC and LG coils increases; thus, the levitation force and guidance force provided by the LG coil increase, and the levitation balanced displacement gradually decreases. Assuming that the trains are at the corresponding levitation balanced displacement and its track center under different Sag and MF, the variation law of the electromagnetic spring coefficient kyy in the y-direction with MF and Sag is shown in Fig. 4. Owing to the increase in MF, the levitation balanced displacement decreases, and the magnetic flux between the LG coil and SC coil decreases. However, the decrease in Sag increases the magnetic flux between the LG and SC coils. Therefore, the combined action of the two causes kyy to initially increase and then decrease.
|
Fig.3 The relationship between levitation balance displacement, MF and Sag at v=600 km/h |
|
Fig.4 The variation law of the electromagnetic spring coefficient kyy |
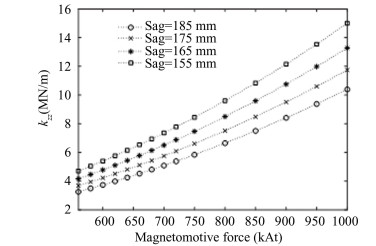
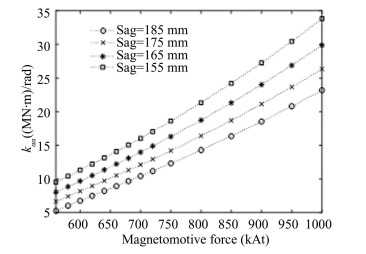
In the z-direction, the variation law of the electromagnetic spring coefficient kzz with the MF and Sag is shown in Fig. 5. kzz gradually increases with an increase in MF and a decrease in Sag. The variation law of the electromagnetic spring coefficient kαα around the x-axis with the MF and Sag is shown in Fig. 6.
|
Fig.5 The variation law of the electromagnetic spring coefficient kzz |
|
Fig.6 The variation law of the electromagnetic spring coefficient kαα |
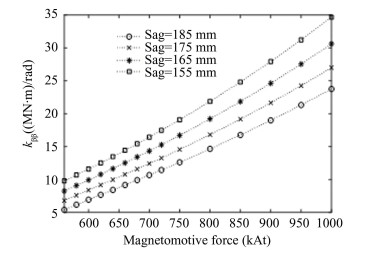
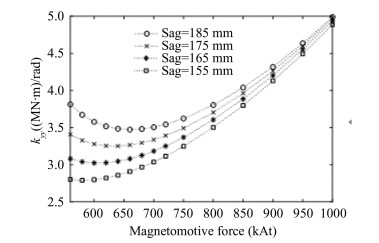
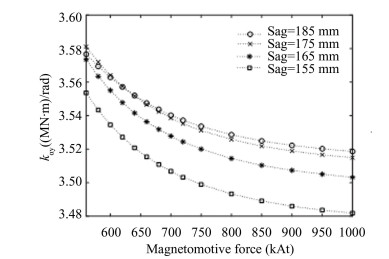
The variation law of the pitch spring coefficient kββ around the y-axis with MF and Sag is shown in Fig. 7. Figs. 6 and 7 indicate that rolling and pitching do not easily occur during superconducting electrodynamic maglev train operation. The variation law of the yaw spring coefficient kyy around the z-axis is shown in Fig. 8. Thekyy first decreased and then increased, because the translation in the y-direction and rolling around the x-axis have strong coupling effects, the characteristics of the coupling electromagnetic spring coefficient kαy between them are shown in Fig. 9. With changes in MF and Sag, kαy gradually decreased.
|
Fig.7 The variation law of the electromagnetic spring coefficient kββ |
|
Fig.8 The variation law of the electromagnetic spring coefficient kyy |
|
Fig.9 The variation law of the electromagnetic spring coefficient kαy |
To evaluate the minimum critical speed when the vehicle starts to operate without auxiliary wheel support and to study the dynamic characteristics of the train, Eqs. (1) and (2) are used to decouple the translation in the y-direction and roll around the x-axis. The characteristics of the equivalent electromagnetic spring coefficient kyeq in the y-direction and the equivalent electromagnetic spring coefficient kαeq around the x-axis are shown in Figs. 10 and 11, respectively.
| $\begin{align*} & k_{y {\rm{eq}}}=\left|\begin{array}{ll} k_{y y} & k_{y \alpha} \\ k_{\alpha y} & k_{\alpha \alpha} \end{array}\right| / k_{\alpha \alpha} \end{align*} $ | (1) |
| $ \begin{align*} & k_{\alpha {\rm{eq}}}=\left|\begin{array}{ll} k_{y y} & k_{y \alpha} \\ k_{\alpha y} & k_{\alpha \alpha} \end{array}\right| / k_{y y} \end{align*} $ | (2) |
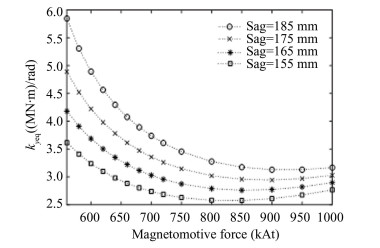
|
Fig.10 The variation law of the electromagnetic spring coefficient kyeq |
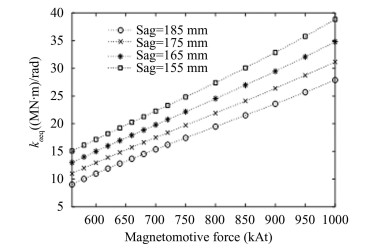
|
Fig.11 The variation law of the electromagnetic spring coefficient kαeq |
2 Research on Stability Operation Control Strategy
The structures of the superconducting coils, levitation and guidance coils, and damping coils of a single bogie are shown in Fig. 12(a), and the positions of the three coils are shown in Fig. 12(b). According to Lenz's law, when the vibration of the bogie changes, the induced current that hinders the vibration of the bogie is generated in the damping coil, and the damping force opposite to the moving direction of the bogie is generated, forcing the bogie to return to the initial state. The parameters of the damping coil are presented in Table 1. Two damping coils were installed on the surface of each superconducting coil. A field-circuit-motion coupling model composed of a single bogie, including a damping coil, LG coil, and SC coil, was established.
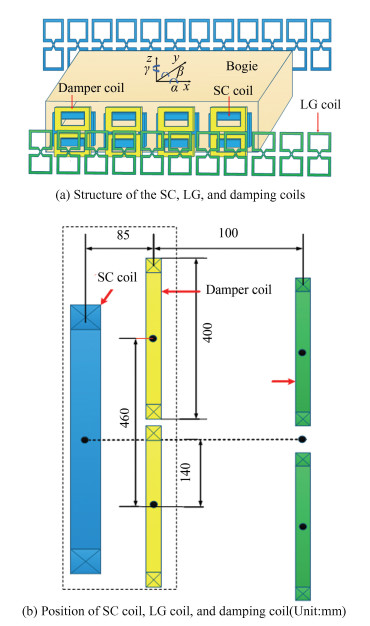
|
Fig.12 The structure and position of SC coil, LG coil and damping coil of single bogie |
| Table 1 Specification for the damper coils |
2.1 Passive Damping Control Strategy
Since there is no excitation outside the damping coil in Fig. 12, this method was defined as a passive damping control strategy. Based on the analysis of electromagnetic spring coefficient, when MF=700 kA, Sag=185 mm, v=600 km/h, combined with the numerical model of single bogie, the dynamic characteristics of bogie under passive damping control strategy are analyzed. The mass of a single bogie is M=2.0×104 kg, and the moments of inertia in different directions are Iy=4.7×104 kg·m2, Iz=7.63× 104 kg·m2, and Ix=3.3×104 kg·m2 respectively. The initial position of the bogie is at the levitation balance displacement and track center, that is (y, z)= (0, -0.03846) m. The initial rotation angle of the bogie is (α, β, γ)=(0.0006, -0.000804, -0.0004), where α, β, and γ are the roll, pitch, and yaw angles of the bogie, respectively. The variation rule of the bogie in different directions with and without the damping coil is shown in Fig. 13. Because the passive damping between the vehicle and track is very small, the displacement attenuation of the vehicle without the damping coil is small. At the same time, when there are other disturbances outside the train, the vibration displacement of the bogie in different directions gradually diverges, resulting in a reduction in train stability. When the bogie is equipped with a damping coil, the vibration displacement of the bogie in different directions gradually converges. This effectively increases the electromagnetic damping of the bogie in different directions, and the convergence speed of the levitation balance displacement, guidance displacement, and roll angle is faster. However, during bogie vibration, the inductance of the damping coil hinders the induced current in the coil. As a result, the polarity of the induced magnetic field in the damping coil cannot be adjusted in real time with the vibration state of the bogie. Therefore, when the bogie vibration direction changes, the damping coil increases the bogie vibration acceleration in a small period of time, and finally increases the stability convergence time of the entire bogie.

|
Fig.13 Displacement variation characteristics of bogie in different directions under without damper coil, and passive damping control strategy |
2.2 Active Damping Control Strategy
An active damping control strategy was adopted, that is, an external voltage was applied to the damping coil according to the vibration characteristics of the bogie. The expression for the voltage applied to the damping coil is given by Eq.(3):
| $ u=\max \left(-k \frac{\mathrm{~d}^2 z}{\mathrm{~d} t^2}, -k \frac{\mathrm{~d}^2 y}{\mathrm{~d} t^2}\right) $ | (3) |
where u is the external voltage applied to the damping coil; z and y are the displacements of the bogie in the z-direction and y-direction, respectively; and k is the voltage coefficient factor. Based on the research on the electromagnetic spring characteristics of a single bogie, combined with the field-circuit-motion coupling model, when the initial conditions of the bogie are the same as in Section 2.1, the characteristics of the bogie in different directions under the passive and active damping control strategies are shown in Fig. 14. As can be seen from Fig. 14, the active damping control strategy effectively reduces the vibration of the bogie in different directions, and with an increase in the voltage coefficient factor, the convergence time of the vibration in different directions of the bogie is significantly shortened, but the damping effect decreases with an increase in the k. Simultaneously, owing to the power loss caused by applying an external voltage to the damping coil under the active damping control strategy, the characteristics of the power loss of a single bogie damping coil with bogie vibration under different voltage coefficient factors are shown in Fig. 15. An increase in the voltage coefficient factor increases the power loss of the damping coil. Therefore, in the process of train operation, an appropriate voltage coefficient factor should be selected according to the vibration of the bogie to shorten the time for the bogie to stabilize under the condition of ensuring a low power loss of the damping coil.

|
Fig.14 Displacement variation characteristics of bogie in different directions under active damping control strategy, and passive damping control strategy |
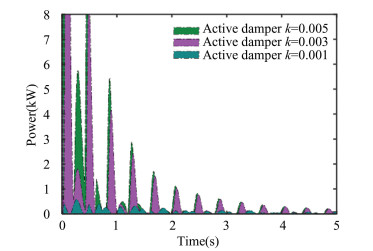
|
Fig.15 Comparative analysis of power consumption of damping coil of single bogie under different voltage coefficient factors |
3 Conclusions
Taking the maglev train of MLX01 type as the research object, this study expounds the variation law of the electromagnetic spring coefficient of a single bogie under different magnetomotive force of the superconducting coil and standard air gap. A passive damping control strategy and an active damping control strategy are designed to increase the electromagnetic damping between the superconducting and ground coils. The vibration rule of the bogie are analyzed, which proved the effectiveness of different damping control strategies in improving the stability of the superconducting electrodynamic maglev train. The main conclusions are as follows.
(1) During train operation, the electromagnetic spring coefficient in the levitation direction is almost linear with the MF of the SC coil, and the train is not easy to roll and pitch. The electromagnetic spring coefficient in the guidance direction and the electromagnetic spring coefficient in the yaw direction first decrease and then increase with an increase in the MF of the SC coil. The coupling electromagnetic spring coefficient between the guidance direction and rolling direction is constant, and the influence of the MF and the Sag can be ignored.
(2) When there was no damping coil, the vibration attenuation of the bogie in different directions was small. When subjected to other external disturbances, the vibrations of the bogie gradually diverge. When the passive damping control strategy is adopted, the displacement in different directions of the bogie gradually converges, and the convergence speeds of the levitation displacement, guidance displacement, and roll angle are faster. However, the polarity of the induced magnetic field in the damping coil cannot be adjusted in real time based on the vibration state of the bogie, which prolongs the convergence time of the vibration stability of the entire bogie.
(3) The active damping control strategy effectively reduces the vibration of the bogie in different directions, and with an increase in the voltage coefficient factor, the convergence time of the vibration of the bogie in different directions is significantly shortened. However, the power loss generated by the damping coil is obviously different under different voltage coefficient factors. Therefore, it is necessary to determine the appropriate voltage coefficient factor according to different external disturbances to reduce the power loss of the damping coil.
(4) During train operation, different damping control strategies should be changed reasonably and in real time according to the size of the external disturbance to minimize the energy consumption of the damping coil, on the premise of meeting the stable operation of the train.
The relevant research results can provide important data support for the design of the damping control strategy and realizes stable operation of maglev trains.
| [1] |
Powell J R, Danby G R. High speed transport by magnetically suspended trains. American Society of Mechanical Engineers, 1966, 66-WARR-5: 1-11. (  0) 0) |
| [2] |
Hao L, Huang Z, Dong F, et al. Study on electrodynamic suspension system with high-temperature superconducting magnets for a high-speed maglev train. IEEE Transactions on Applied Superconductivity, 2019, 29(2): 3600105. DOI:10.1109/TASC.2018.2881688 (  0) 0) |
| [3] |
Reitz J R. Forces on moving magnets due to eddy currents. Journal of Applied Physics, 1970, 41(5): 2067-2071. DOI:10.1063/1.1659166 (  0) 0) |
| [4] |
He J L, Rote D M, Coffey H T. Electrodynamic forces of the cross-connected figure-eight null-flux coil suspension system. Proceedings of 13th International Conference on Magnetically Levitated Systems and Linear Drives. Illinois, 1993, 6: 64-70. (  0) 0) |
| [5] |
Murai T, Fujiwara S. Characteristics of linear synchronous motor combined propulsion, levitation and guidance. Proc. Int. Cod. Speedup Technol. Railway Maglev Vehicles, 1993,, 5(11): 22-26. (  0) 0) |
| [6] |
Yoshika H, Watanahe K. Dynamic characteristics of side-wall magnetically levitated vehicle. Int. Cod. on Speedup Technology for Railway and Maglev Vehicles, 1993, 11: 22-26. (  0) 0) |
| [7] |
Wang Z, Cai Y, Gong T, et al. Study on characteristics of superconducting electric levitation train based on field road motion coupling model. Chinese Journal of Electrical Engineering, 2019, 39(4): 1162-1171. DOI:10.13334/j.0258-8013.pcsee.180798 (  0) 0) |
| [8] |
Ono M, Koga S, Ohtsuki H. Japan's superconducting maglev train. IEEE Instrumentation & Measurement Magazine, 2002, 5(1): 9-15. DOI:10.1109/5289.988732 (  0) 0) |
| [9] |
Nagashima K. Research and development concerning superconducting maglev and research on applying its technology to conventional railways system. Quarterly Report of RTRI, 2016, 57(3): 175-178. DOI:10.2219/rtriqr.57.3_175 (  0) 0) |
| [10] |
He J L, Rote D M, Coffey H T. Applications of the dynamiccircuit theory to maglev suspension systems. IEEE Transactions on Magnetics, 1993, 29(6): 4153-4164. DOI:10.1109/20.280868 (  0) 0) |
| [11] |
Yonezu T, Watanabe K, Suzuki E, et al. Characteristics of magnetic springs for guidance of superconducting maglev vehicles. Quarterly Report of RTRI, 2018, 59(4): 293-298. DOI:10.2219/rtriqr.59.4_293 (  0) 0) |
| [12] |
Yonezu T, Watanabe K, Suzuki E. Fundamental study on effect of gap reduction on EDS and LSM characteristics of superconducting maglev vehicles. The 23rd International Conference on Magnetically Levitated Systems and Linear Drives (MAGLEV 2016), 2016, A03. (  0) 0) |
| [13] |
Watanabe K, Yoshioka H, Suzuki E, et al. A study of vibration control systems for superconducting maglev vehicles (vibration control of lateral and rolling motions). Journal of System Design and Dynamics, 2007, 1(3): 593-604. DOI:10.1299/jsdd.1.593 (  0) 0) |
| [14] |
Xu Y L, Wang Z L, Li G Q, et al. High-speed running maglev trains interacting with elastic transitional viaducts. Engineering Structures, 2019, 183: 562-578. DOI:10.1016/j.engstruct.2019.01.012 (  0) 0) |
| [15] |
Wang Z L, Xu Y L, Li G Q, et al. Modelling and validation of coupled high-speed maglev train-and-viaduct systems considering support flexibility. International Journal of Vehicle Mechanics and Mobility, 2018, 57(2): 161-191. DOI:10.1080/00423114.2018.1450517 (  0) 0) |
| [16] |
Wang Z L, Xu Y L, Li G Q, et al. Dynamic analysis of a coupled system of high-speed Maglev train and curved viaduct. International Journal of Structural Stability and Dynamics, 2018, 18(11): 1-32. DOI:10.1142/S0219455418501432 (  0) 0) |
| [17] |
Li G Q, Wang Z L, Chen S, et al. Field measurements and analyses of environmental vibrations induced by high-speed Maglev. Science of The Total Environment, 2016, 568: 1295-1307. DOI:10.1016/j.scitotenv.2016.01.212 (  0) 0) |
| [18] |
Wang X, Huang J. Study on electromagnetic relationship and dynamic characteristics of superconducting electrodynamic maglev train on curved track. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(6): 6146-6164. DOI:10.1109/TITS.2023.3248078 (  0) 0) |
| [19] |
Wang X, Huang J. Research on electromagnetic relationship and passive electromagnetic damping characteristics of superconducting electrodynamic maglev train. IEEE Transactions on Applied Superconductivity, 2022, 32(7): 3602618. DOI:10.1109/TASC.2022.3182051 (  0) 0) |
| [20] |
Fujimoto T, Aiba M, Suzuki H, et al. Characteristics of electromagnetic force of ground coil for levitation and guidance at the Yamanashi maglev test line. Quarterly Report of RTRI, 2000, 41(2): 63-67. DOI:10.2219/rtriqr.41.63 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


