2. Shanghai Key Laboratory of Rail Infrastructure Durability and System Safety, Tongji University, Shanghai 201804, China;
3. Shanghai Collaborative Innovation Research Center for Multi-Network & Multi-Modal Rail Transit, Tongji University, Shanghai 201804, China
Urban rail transit, as one of the public transport modes in big cities, has the characteristics of large capacity, fast speed and high punctuality, which has positive significance for alleviating the surface traffic congestion in China. However, the rapid growth of the population outside the city also brings new challenges and pressures for urban rail transit organizations. The representative performance is the low frequency of service at suburban stations during commuting peak hours. For example, Shanghai Metro stations, such as Xinzhuang, Shendu Highway, Luheng Road, Cao Road and other stations located in the far ends of the city are forced to implement normal passenger flow restrictions during morning peak hours due to insufficient train flow. It is necessary to use the available rolling stocks as efficiently as possible and improve the service frequency of suburban stations under the condition of a limited number of rolling stock.
In real life, the metro system adopts relatively simple line plans, so that the rolling stocks are not efficiently used. For example, some lines only offer the full-length services, with all stops being serviced equally, which, however, requires a large number of rolling stocks to achieve a high level of service frequency. In other lines, the full-length service and short-length (short-turn) services are mixed, which can reduce the number of rolling stocks required. However, in real life, the short-length services only stop at stations in the city center or busy zones, the stations in suburban areas are not well served. Given this situation, this paper focuses on optimizing the line plan (full-length and short-length services), train timetable and rolling stock circulation of a metro line, considering the limited number of rolling stocks in order to provide better services and save operational costs.
1 Literature ReviewIn the research of urban rail transit organization, providing maximum transport service with a limited number of rolling stock is a research issue. The operation of rolling stock circulation and line plan, from the perspective of train scheduling, needs to be researched.
1) Subway line planning
In the line plan problem, designing an optimal line plan is a research challenge.
In the existing studies, Xu et al. [1] proposed the basic principles of the transportation organization of urban rail transit lines, compared and analyzed the characteristics of different services from the aspects of passenger service, traffic capacity and rolling stock, and gave suggestions on train services design. Niu et al.[2] constructed a model for the line plan considering a single full-length services with the train operation requirements, the number of rolling stocks and the interests of the operating enterprises serving as the constraint conditions and the minimum waiting time of passengers serving as the objective function. Xu et al.[3] proposed two operation modes: full-length service and short-length service ratio of 1∶m and m∶1. They also built an optimization model for a full-length and short-length service scheme suitable for multi-formation considering the train headway in common line sections. Wang et al.[4] constructed a model to minimize passenger travel costs and enterprise operation costs, analyzing the full-length services and short-length services modes under the condition that the number of each service is given. Dai et al.[5] established a MINLP optimization model with the goal of reducing the average waiting time of passengers, increasing the average load factor of trains, and reducing the total kilometers traveled by mixed full-length and short-length services.
2) Integrated optimization of rolling stock circulation and line planning
In the integrated optimization of rolling stock circulation and line planning problem, the main focus is to use the relatively limited number of rolling stock to complete the line plan.Given a relatively fixed train timetable, the objective is to assign different rolling stocks to different line plans.
For example, Cadarso et al.[6] solved rolling stock assignment and the train service problems to obtain better and more robust solutions, and proposed a heuristic based on Benders decomposition for computational reasons. Giacco et al.[7] used a two-step approach to solve rolling stock rostering and maintenance scheduling with limited rolling stock.Cadarso et al.[8] proposed an integrated planning model to solve the problem of railway timetable and rolling stock assignment for attending the increased passenger demand.Ying et al.[9] presented a novel actor-critic deep reinforcement learning approach for scheduling metro trains with circulation of limited rolling stock by Markov decision process.Haahr et al.[10] used a column and row generation approach to solve an optimization model of rolling stock (re)scheduling by performing tests with different disruption scenarios. Jiang et al.[11] established a MINLP optimization model under the conditions of full-length and short-length services independent operation, and full-length and short-length services mixed operation for rolling stocks based on the four basic service forms of common line section.Lusby et al.[12] proposed a branch-and-price algorithm to solve the collaborative optimization model of the turnover of rolling stock rescheduling considering the train service mode.Yue et al.[13] proposed a model that integrates both train timetabling and rolling stock scheduling based on time-dependent passenger flow demands and taking into account rolling stock and service requirements. Xu et al.[14] studied the characteristics of the periodic train timetable and analyzed the calculation method for line capacity and rolling stock circulation in the metro line that offers a mix of full-length and short-length services. Wang et al.[15] presented an integrated MILP model to optimize the train schedule and circulation plan simultaneously based on given full-length services generated by the demand analysis and line planning. Liu et al.[16] proposed a model for metro train scheduling and train services combined on a bi-directional metro line considering turnaround operations and the entering/exiting depot with a Lagrangian relaxation-based approach.Wang et al. [17] presented an integrated MILP model to optimize the train schedule and circulation plan simultaneously based on a given service pattern generated by the demand analysis and line planning.Zhang et al.[18] considered the train scheduling with short turning strategy for an urban rail transit line with multiple depots and the utilization of trains.Wang et al.[19] used a two-stage optimization approach to optimize the train schedule and circulation plan with consideration of passenger demand for an urban rail transit line.Peeters et al.[20] described a model and a branch-and-price algorithm to solve an efficient rolling stock circulation on a set of interacting train lines. Ying et al.[21] proposed a deep reinforcement learning method for metro train scheduling with the limited rolling stocks operation under a single service, and constructed an optimization model with the objective function of minimizing cost.
Table 1 shows the comparison of this study and the most relevant studies. In the existing studies, the research problems include three aspects: timetable, rolling stock circulation and line plan. The research mainly used Branch-and-Price, Lagrangian relaxation, Two-stage and other algorithms to solve the model.
| Table 1 Comparison of this study and relevant studies |
However, the factors considered in the existing studies were not very comprehensive, mainly including the following four aspects:
1) Existing studies have not distinguished the differences in the values of various time parameters in different operating periods within a day. Only one speed scale was used, and the speed scale of train operation was not considered to be different in different time periods.
2) Yue et al.[13], Wang et al.[15], and Wang et al.[19] studied rolling stock circulation with full-length services. But, it lacks consideration of the combination of full-length and short-length.
3) Xu et al.[3], Wang et al.[4], Dai et al.[5] and Zhang et al.[18] studied the mixing of full-length service and short-length service. But, the full-length service and short-length service were dispatched in a fixed proportion, which limited certain flexibility.
4) Jiang et al.[11], Wang et al.[17] and Wang et al.[19] studied rolling stock circulation with the minimum number of rolling stocks as the optimization goal. But, they did not further consider the full utilization of rolling stocks to provide maximum transport capacity for passengers under the condition of rolling stock limitation.
This paper focuses on the integrated optimization of timetable, rolling stock circulation and line plan to solve the problem of transportation capability shortage under large passenger flow. The line plan considers the mixed usages of short-length and full-length services to make it more flexible. Trains use different speed scales for different periods of time according to the actual transport organization of urban rail transit. We consider providing maximum number of full-length services to meet passenger flow demand within the limit of rolling stocks. A MINLP model is proposed, and a two-stage algorithm is used to solve the model.
To sum up, in the existing line plan, the number of services and the proportion of services are relatively fixed with limited number of rolling stocks, it is unfavorable to generate full-length services. It is necessary to appropriately relax the constraints on the line plan.
Compared with existing researches, the main highlights of this study are as follows:
(a) This paper focuses on the integrated optimization of timetable, rolling stock circulation and line plan. A MINLP model is developed for the studied problem. Mixed usage of full-length and short-length services is proposed. The existing mode of either a single full-length service or short-length service for a rolling stock is changed. This alteration enables the combination of both full-length service and short-length service for rolling stock. Restrictions on the use of rolling stock are lifted, leading to a more diverse circulation of rolling stock.
(b) The model adopts a two-stage algorithm to solve the problem. First, the train timetable of the full-length service of the whole line is solved. Second, on the basis of calculating the train timetable, the matching between the rolling stock circulation and line plan is solved by shortening some full-length services to short-length services.Besides, relevant auxiliary variables are introduced to transform the nonlinear model into linear model.
The remainder of this paper proceeds as follows. In Section 2, the problem statement is presented. Section 3 introduces an integrated optimization model of rolling stock circulation and train service scheme. Section 4 presents two-step solving process. Section 5 conducts numerical experiments to verify the proposed model. Section 6 summarizes the whole paper and looks forward to further research in the future.
2 Problem StatementsFig. 1 shows the structure of the studied metro corridor. There are four stations in this corridor, stations A, B, C, and D, which allow the turnaround operations. Station A and station D are connected to two depots, respectively. A train service in this corridor may start/end its services only from/at the four stations. The study names the train services from A to D (A→D) and from D to A (D→A) as the full-length train services, the train services B→C, C→B, A→C, C→A, B→D, D→B etc. as the short-length services. A mixture of short-length and full-length services can provide more efficient and flexible services for passengers. However, the complexity of the train timetabling and rolling stock circulation problems will increase. The train timetabling problem dictates the train arrival, departure, and dwell times at each station and the running times between stations. The rolling stock circulation plan defines the connections between the downward and upward trains at the turnaround stations.
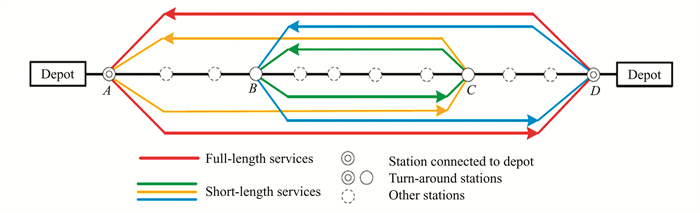
|
Fig.1 Illustration of full-length and short-length train services |
Fig. 2 shows an example of the mixed use of short-length and full-length services. Rolling stock 1 exits the depot and sequentially provides services to the train services A→D, D→B, B→C, C→A, A→C, C→B, and B→D one by one. After completing its service of the day, it stops at the depot close to station D. Rolling stock 1 executes both the full-length services and the short-length services. Compared with the common cases, in which one rolling stock can only execute short-length or full-length services, the mixed usage of short-length and full-length services can utilize the rolling stock more efficiently. In other words, if the total number of rolling stocks to provide services in this corridor is limited, the mixed usage of short-length and full-length services can be a good strategy to make better use of the rolling stocks and provide more services to passengers.
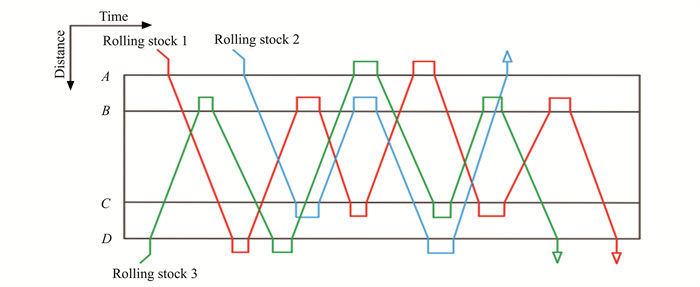
|
Fig.2 An example of the mixed use of short-length and full-length services |
This study optimizes the rolling stock circulation and the train timetable simultaneously, considering the mixed usage of short-length and full-length services. Its objectives are to reduce the number of rolling stocks in order to reduce the operational costs, and to increase the number of full-length services to provide more services to passengers at stations located between A and B (C and D, not including station B and C). The proposed method adopts a two-stage algorithm (Section 4). In the first stage, it is assumed that all the train services are full-length services. The timetable of those full-length services is optimized. The train running time in each section is considered as constant values, but each train service may have different speed scales, so that each train service has different running times. It is assumed that one rolling stock can perform different speed scales in different train services.
In the second stage, the optimized timetable of those full-length services is taken as the inputs, the rolling stock circulation plan is optimized considering the constraints of limited number of rolling stocks and the fleet size balance. In this study, the number of rolling stocks is limited, which means the number of rolling stocks may not be enough to perform all the full-length services as assumed in the first stage. Therefore, the second stage aims to shorten some full-length services into short-length services to ensure feasible rolling stock circulation. The circulation is achieved by connecting all the services to depots or to the train services from the opposite directions. In addition, the fleet size balance in depots is considered. That is, for each depot, the second stage builds constraints to ensure that the number of rolling stocks that exit that depot at the beginning of the day is equal to the number of rolling stocks that enter the depot at the end of the day.
3 Integrated Optimization Model 3.1 Model Assumptions1) The train running time in each section is fixed, and the train running time of different speed scales is strictly based on the parameters of train operation diagram.
2) Consider the flexibility of the use of rolling stocks, a rolling stock exits from a certain depot, after the execution of a number of train services, it can enter into any depot.It is necessary to ensure that the number of rolling stock entering and exiting depot should be equal in a day.
3) The same rolling stock can perform a variety of speed scales throughout the whole operation. For different line plans, according to the actual needs, different speed scales can be flexibly implemented.
4) Each time parameter is given a minimum technical numerical value, such as headway time, dwelling time, and turnaround operation time, in order to meet the needs of passengers during peak period.
5) The overtaking of trains does not occur in normal operations of urban rail transit lines, where trains usually run in a sequential order.
6) The rolling stocks can operate from the early morning to the late evening. The maximum number of train services that a rolling stock can operate is not considered.
3.2 Parameters and Decision VariablesThe parameters and the decision variables are defined in Table 2 and Table 3.
| Table 2 Parameter descriptions |
| Table 3 Decision variables descriptions |
3.3 Constraints
1) Train running time constraints.
(a) Train section running time constraints:
| $ \underline{a}_{s+1}^{l, v}=\underline{d}_s^{l, v}+\underline{t}_s^v, \forall l \in L^{\mathrm{down}}, s \in[1,2, \cdots, S-1],\\v \in[0,1] $ | (1) |
| $ \bar{a}_{s-1}^{l, v}=\bar{a}_s^{l, v}+\bar{t}_{s-1}^v, \forall l \in L^{\text {up }}, s \in[2,3, \cdots, S],\\v \in[0,1] $ | (2) |
(b) Train dwelling time constraints:
| $ \underline{d}_s^{l, v} \geqslant \underline{a}_s^{l, v}+t^{\text {dwell, min }}, \forall l \in L^{\text {down }}, s \in \\ [2,3, \cdots, S-1], v \in[0,1] $ | (3) |
| $ \underline{d}_s^{l, v} \leqslant \underline{a}_s^{l, v}+t^{\mathrm{dwell}, \max }, \forall l \in L^{\mathrm{down}}, s \in \\ [2,3, \cdots, S-1], v \in[0,1] $ | (4) |
| $ \bar{d}_s^{l, v} \geqslant \bar{a}_s^{l, v}+t^{\text {dwell, min }}, \forall l \in L^{\text {up }}, s \in \\ [2,3, \cdots, S-1], v \in[0,1] $ | (5) |
| $ \bar{d}_s^{l, v} \leqslant \bar{a}_s^{l, v}+t^{\mathrm{dwell}, \max }, \forall l \in L^{\mathrm{up}}, s \in \\ [2,3, \cdots, S-1], v \in[0,1] $ | (6) |
2) Train headway constraints.
(a) Departure-departure headway constraints:
| $ \underline{d}_s^{l+1, v^{\prime}}-\underline{d}_s^{l, v} \geqslant h_{v, v}^{\mathrm{dd}}, \forall l \in L^{\mathrm{down}} /\{L-1\}, \\ s \in[1,2, \cdots, S-1], v \in[0,1] $ | (7) |
| $ \bar{d}_s^{l+1, v^{\prime}}-\bar{d}_s^{l, v} \geqslant h_{v, v}^{\mathrm{dd}}, \forall l \in L^{\mathrm{up}} /\{L-1\},\\ s \in[2,3, \cdots, S], v \in[0,1] $ | (8) |
(b) Arrival-arrival headway constraints:
| $ \underline{a}_s^{l+1, v^{\prime}}-\underline{a}_s^{l, v} \geqslant h_{v, v^{\prime}}^{\mathrm{aa}}, \forall l \in L^{\mathrm{down}} /\{L-1\},\\ s \in[2,3, \cdots, S], v \in[0,1] $ | (9) |
| $ \bar{a}_s^{l+1, v^{{\prime}}}-\bar{a}_s^{l, v} \geqslant h_{v, v^{\prime}}^{\mathrm{aa}}, \forall l \in L^{\mathrm{up}} /\{L-1\},\\ s \in[1,2, \cdots, S-1], v \in[0,1] $ | (10) |
3) Service uniqueness constraints.
Each train service can only have one unique line plan (i.e. full-length or short length), which is guaranteed by
| $ \sum\limits_{j \in J^{\text {down }}} \underline{\theta}_{j, l}=1, \forall l \in L^{\text {down }} $ | (11) |
| $ \sum\limits_{j \in J ^\text { up }} \bar{\theta}_{j, l}=1, \forall l \in L^{\text {up }} $ | (12) |
4) Train flow balance constraints at turnaround stations.
(a) The number of ending trains in the downward direction is equal to the number of starting trains in the upward direction.
| $ \sum\limits_{l \in L^{\text {down }}} \sum\limits_{j \in J^{\text {down }}} \underline{\theta}_{j, l} \cdot{\underline{e}}_{s, j} \cdot{\underline{z}}_s= \sum\limits_{l \in L^{\text {up }}} \sum\limits_{j \in J^{\text {up }}} \bar{\theta}_{j, l} \cdot \bar{o}_{s, j} \cdot{\underline{z}_s},\\ \forall s \in S $ | (13) |
| $ \sum\limits_{l \in L^{\text {down }}} \sum\limits_{j \in J^{\text {down }}}\underline{\theta}_{j, l} \cdot {\underline{e}}_{s, j} \cdot \underline{k}_s= \sum\limits_{l \in L^{\text {up }}} \sum\limits_{j \in J ^\text { up }} \bar{\theta}_{j, l} \cdot \bar{o}_{s, j} \cdot{\underline{k}}_{s},\\ \forall s \in S $ | (14) |
(b) The number of ending trains in the upward direction is equal to the number of starting trains in the downward direction.
| $ \sum\limits_{l \in L^{\text {up }}} \sum\limits_{j \in J^ \text { up }} \bar{\theta}_{j, l} \cdot \bar{e}_{s, j} \cdot \bar{z}_s=\sum\limits_{l \in L^{\text {down }}} \sum\limits_{j \in J^{\text {down }}} \underline{\theta}_{j, l} \cdot{\underline{ o} _{s, j} \cdot \bar{z}_s },\forall s \in S $ | (15) |
| $ \sum\limits_{l \in L^{\text {up }}} \sum\limits_{j \in J^ \text { up }} \bar{\theta}_{j, l} \cdot \bar{e}_{s, j} \cdot \bar{k}_s=\sum\limits_{l \in L^{\text {down }}} \sum\limits_{j \in J^{\text {down }}} \underline{\theta}_{j, l} \cdot{\underline{ o} _{s, j} \cdot \bar{k}_s },\forall s \in S $ | (16) |
5) Rolling stock circulation constraints.
(a) After a rolling stock executes a certain train service, it can either go back to a depot or turn around at a station to execute the train service in the opposite direction. That is achieved by
| $ (1-\underline{\beta}_l) \cdot \sum\limits_{j \in J ^\text { down }} \sum\limits_{s \in S} \underline{\theta}_{j, l} \cdot \underline{e}_{s, j} \cdot \underline{z}_s+\underline{\beta}_l \cdot \sum\limits_{j \in J^{\text {down }}} \sum\limits_{s \in S} \underline{\theta}_{j, l}\cdot \\ \underline{e}_{s, j} \cdot \underline{k}_s=1, \forall l \in L^{\mathrm{down}} $ | (17) |
| $ \left(1-\bar{\beta}_l\right) \cdot \sum\limits_{j \in J ^\text { up }} \sum\limits_{s \in S} \bar{\theta}_{j, l} \cdot \bar{e}_{s, j} \cdot \bar{z}_s+\bar{\beta}_l \cdot \sum\limits_{j \in J ^\text { up }} \sum\limits_{s \in S} \bar{\theta}_{j, l} \cdot \\ \bar{e}_{s, j} \cdot \bar{k}_s=1, \forall l \in L^{\mathrm{up}} $ | (18) |
(b) Similarly, for any train service, its rolling stock may either come from a depot, or from a train service of the opposite direction. That is
| $ \left(1-\underline{\alpha}_{l}\right) \cdot \sum\limits_{j \in J^ \text { down }} \sum\limits_{s \in S} \underline{\theta}_{j, l} \cdot \underline{e}_{s, j} \cdot \bar{z}_s+\underline{\alpha}_l \cdot \sum\limits_{j \in J ^\text { down }} \sum\limits_{s \in S} \underline{\theta}_{j, l} \cdot \underline{e}_{s, j} \cdot \bar{k}_s=1, \forall l \in L^{\mathrm{down}} $ | (19) |
| $ \left(1-{\underline{\alpha}}_l\right) \cdot \sum\limits_{j \in J^\text { up }} \sum\limits_{s \in S} \bar{\theta}_{j, l} \cdot \bar{o}_{s, j} \cdot \underline{z}_s+{\underline{\alpha}}_l \cdot \sum\limits_{j \in J ^\text { up }} \sum\limits_{s \in S} \bar{\theta}_{j, l} \cdot \bar{o}_{s, j} \cdot \underline{k}_s=1, \forall l \in L^{\text {up }} $ | (20) |
(c) If a downward train is turned around and becomes an upward train, constraints are needed to respect the minimum turn-around time restriction. That is
| $ \bar{d}_s^{l^{\prime}, v} \cdot \sum\limits_{j \in J^ \text { up }} \sum\limits_{s \in S}\left(\bar{o}_{s, j} \cdot \bar{\theta}_{j, l^{\prime}}\right) -{\underline{a}}_s^{l, v} \cdot \sum\limits_{j \in J^{\text {down }}} \sum\limits_{s \in S}\left({\underset{-}{e}}_{s, j} \cdot\right. \left.\underline{\theta}_{j, l}\right) \geqslant t^{\mathrm{re}, \min } \cdot \\ \underline{m}_{l, l^{\prime}}-M \cdot\left(1-\underline{m}_{l, l^{\prime}}\right), \forall l \in L^{\text {down }}, \forall l^{\prime} \in L^{\text {up }} $ | (21) |
| $ \bar{d}_s^{l^{\prime}, v} \cdot \sum\limits_{j \in J^ \text { up }} \sum\limits_{s \in S}\left(\bar{o}_{s, j} \cdot \bar{\theta}_{j, l^{\prime}}\right) -{\underline{a}}_s^{l, v} \cdot \sum\limits_{j \in J^{\text {down }}} \sum\limits_{s \in S}\left({\underline{e}}_{s, j} \cdot\right. \left.\underline{\theta}_{j, l}\right) \leqslant t^{\mathrm{re}, \max } \cdot \\ \underline{m}_{l, l^{\prime}}-M \cdot\left(1-\underline{m}_{l, l^{\prime}}\right), \forall l \in L^{\text {down }}, \forall l^{\prime} \in L^{\text {up }} $ | (22) |
(d) If an upward train is turned around and becomes a downward train, constraints are needed to respect the minimum turnaround time restriction. That is,
| $ \underline{d}_s^{l, v} \cdot \sum\limits_{j \in J^{\mathrm{down}}} \sum\limits_{s \in S}\left(\underline{o}_{s, j} \cdot \underline{\theta}_{j, l}\right)-\bar{a}_s^{l^{\prime}, v} \cdot \sum\limits_{j \in J^{\text {up }}} \sum\limits_{s \in S}\left(\bar{e}_{s, j} \cdot\right.\\ \left.\bar{\theta}_{j, l^{\prime}}\right) \geqslant t^{\mathrm{re}, \min } \times \bar{m}_{l^{\prime}, l}-M \times\left(1-\bar{m}_{l^{\prime}, l}\right), \forall l \in\\ L^{\text {down }}, \forall l^{\prime} \in L^{\text {up }} $ | (23) |
| $ \underline{d}_s^{l, v} \cdot \sum\limits_{j \in J^{\mathrm{down}}} \sum\limits_{s \in S}\left(\underline{o}_{s, j} \cdot \underline{\theta}_{j, l}\right)-\bar{a}_s^{l^{\prime}, v} \cdot \sum\limits_{j \in J^{\text {up }}} \sum\limits_{s \in S}\left(\bar{e}_{s, j} \cdot\right.\\ \left.\bar{\theta}_{j, l^{\prime}}\right) \leqslant t^{\mathrm{re}, \max } \times \bar{m}_{l^{\prime}, l}-M \times\left(1-\bar{m}_{l^{\prime}, l}\right), \forall l \in\\ L^{\text {down }}, \forall l^{\prime} \in L^{\text {up }} $ | (24) |
(e) To reduce the invalid search range in the solution process and ensure the adjacent upward and downward services can be connected, the following two constraints are built:
| $ \left(l-l^{\prime}-1\right) \cdot \bar{m}_{l^{\prime}, l} \geqslant 0, \forall l \in L^{\mathrm{down}}, \forall l^{\prime} \in L^{\text {up }} $ | (25) |
| $ \left(l^{\prime}-l-1\right) \cdot \underline{m}_{l, l^{\prime}} \geqslant 0, \forall l \in L^{\mathrm{down}}, \forall l^{\prime} \in L^{\text {up }} $ | (26) |
(f) If a train service does not go back to any depot after finish its service, it must turn-around and become a train service of the opposite direction. That is
| $ \sum\limits_{l^{\prime} \in\left[2, \cdots, L^{\text {up }}\right]} \underline{m}_{l, l^{\prime}} =1-\underline{\beta}_l, \forall l \in \\\left[1,2, \cdots, L^{\text {down }}-1\right] $ | (27) |
| $ \sum\limits_{l \in\left[2, \cdots, L^{\mathrm{down}}\right]} \bar{m}_{l^{\prime}, l}=1-\bar{\beta}_{l^{\prime}}, \forall l^{\prime} \in \left[1,2, \cdots, L^{\text {up }}-1\right] $ | (28) |
If the rolling stock of a train service is not from a depot, it must come from the train service of the opposite direction. That is
| $ \sum\limits_{l^{\prime} \in\left[1,2, \cdots, L^{\text {up }}-1\right]} \bar{m}_{l^{\prime}, l} =1-\underline{\alpha}_l, \forall l \in\left[2,3, \cdots, L^{\text {down }}\right] $ | (29) |
| $ \sum\limits_{l \in\left[1,2, \cdots, L^{\text {down }}-1\right]} \underline{m}_{l, l^{\prime}}=1-\bar{\alpha}_{l^{\prime}}, \forall l^{\prime} \in\left[2,3 \cdots, L^{\mathrm{up}}\right] $ | (30) |
(g) For a downward train service l∈Ldown and an upward train service l' ∈Lup, the two train services can be only connected if the end station of the first train is the same as the end station of the following train.
| $ \underline{m}_{l, l^{\prime}}\cdot \sum\limits_{j \in J^ \text { down }} \underline{\theta}_{j, l}\cdot{\underline{e}}_{s, j} \cdot{\underline{z}}_{s} ={\underline{m}}_{l, l^{\prime}} \cdot \sum\limits_{j \in J^ \text { up }} \bar{\theta}_{j, l^{\prime}} \cdot \bar{o}_{s, j} \cdot{\underline{z}}_s,\\ \forall s \in S, \forall l \in L^{\text {down }}, \forall l^{\prime} \in L^{\text {up }} $ | (31) |
| $ \bar{m}_{l^{\prime}, l} \cdot \sum\limits_{j \in J ^\text { up }} \bar{\theta}_{j, l^{\prime}} \cdot \bar{e}_{s, j} \cdot \bar{z}_s =\bar{m}_{l^{\prime}, l} \cdot \sum\limits_{j \in J^{\text {down }}} \underline{\theta}_{j, l} \cdot{\underline{o}_{s, j}} \cdot \bar{z}_s,\\ \forall s \in S, \forall l \in L^{\text {down }}, \forall l^{\prime} \in L^{\text {up }} $ | (32) |
6) Minimum service frequency constraints.
To ensure a certain frequency of services in the downward direction, specific constraints are added to the first station (s=1), to ensure that xb out of xa train services must start from the first station(s=1).
| $ \begin{array}{r}\sum\limits_{l \in\left[l, \cdots, l+x_{\mathrm{a}}-1\right]} \underline{\theta}_{j, l} \cdot \bar{o}_{1, j} \geqslant x_{\mathrm{b}}, \forall l \in \\ {\left[1,2, \cdots, L^{\text {down }}-x_{\mathrm{a}}\right]}\end{array} $ | (33) |
To ensure a certain frequency of services in the downward direction, specific constraints are added to the last station (s=S), to ensure that xd out of xc train services must end in the last station(s=S).
| $ \sum\limits_{l \in\left[l, \cdots, l+x_{\mathrm{c}}-1\right]} \underline{\theta}_{j, l} \cdot {\underline{e}}_{S, j} \geqslant x_{\mathrm{d}}, \forall l \in\\ \left[1,2, \cdots, L^{\text {down }}-x_{\mathrm{c}}\right] $ | (34) |
To ensure a certain frequency of services in the upward direction, specific constraints are added to the first station (s=S), to ensure that xf out of xe train services must start from the first station(s=S).
| $ \sum\limits_{l \in\left[l, \cdots, l+x_{\mathrm{e}}-1\right]} \bar{\theta}_{j, l} \cdot \bar{o}_{S, j} \geqslant x_{\mathrm{f}}, \forall l \in\\ \left[1,2, \cdots, L^{\text {up }}-x_{\rm{e}}\right] $ | (35) |
To ensure a certain frequency of services in the upward direction, specific constraints are added to the last station (s=1), to ensure that xh out of xg train services must end in the last station(s=1).
| $ \sum\limits_{l \in\left[l, \cdots, l+x_{\mathrm{g}}-1\right]} \bar{\theta}_{j, l} \cdot \bar{e}_{1, j} \geqslant x_{\mathrm{h}}, \forall l \in\\ \left[1,2, \cdots, L^{\text {up }}-x_{\mathrm{g}}\right] $ | (36) |
7) Fleet size balance at depots.
For a depot, the number of rolling stocks entering and exiting during the day should be equal.
| $ \sum\limits_{l \in L^{\text {down }}} \underline{\alpha}_l=\sum\limits_{l^{\prime} \in L^{\text {up }}} \bar{\beta}_{l^{\prime}} $ | (37) |
| $ \sum\limits_{l \in L^{\mathrm{down}}} \bar{\alpha}_l=\sum\limits_{l^{\prime} \in L^{\text {up }}} \underline{\beta}_{l^{\prime}} $ | (38) |
Constraints (17)-(20), (31)-(32) are nonlinear, which need to be linearized by the following principle in Eq.(39). a, b, c are all 0-1 variables. c is a newly-introduced binary variable to replace the nonlinear part (a·b) in constraints (17)-(20), (31)-(32). a, b, and c must respect the constraints in the right side in Eq. (39).
| $ c=a \cdot b \Rightarrow\left\{\begin{array}{l} a \geqslant c \\ b \geqslant c \\ c \geqslant a+b-1 \\ a, b, c \in[0,1] \end{array}\right. $ | (39) |
The integrated optimization method involves a train timetable optimization model, denoted as model F1. The optimization objective is to minimize the sum of the arrival times of the last train services at the end stations, so that the train timetable is compressed as much as possible.
Model F1:
| $ \min J_1=\underline{a}_S^{L^{\text {down }}, v}+\bar{a}_1^{L^{\text {up }}, v}\\{\rm { s.t.\;\; Constraints (1)-(10) }} $ | (40) |
The second part of the integrated optimization method is a rolling stock circulation optimization model, denoted as a MINLP model F2. The optimization objective is to minimize the total number of train services coming from depots, in order to achieve the purpose of saving the use of rolling stocks. F2 takes the optimized timetable of F1 as the input, in which the timetable only contains the full-length services.
Model F2:
| $ \begin{aligned} \min J_2=\sum\limits_{l \in L^{\text {down }}} \underline{\alpha}_l+\sum\limits_{l \in L^{\text {up }}} \bar{\alpha}_l\\ {\rm { s.t.\;\; Constraints }}(11)-(38) . \end{aligned} $ | (41) |
The solution of F2 ensures the minimum number of rolling stocks, but cannot ensure the maximum number of full-length services. To go further, a rolling stock circulation optimization model is defined, denoted as F3, which focuses on the situation that the given number of rolling stocks is limited, so that it is necessary to shorten some full-length services into short-length services to ensure a feasible circulation. The optimization objective of F3 is to maximize the number of full-length services, to provide more services to passengers at stations located between A and B (C and D, not including station B and C in Fig. 2).
Model F3:
| $ \max J_3=\sum\limits_{l \in L^{\text {down }}} \underline{\theta}_{j, l}+\sum\limits_{l \in L^{\text {up }}} \bar{\theta}_{j, l}\\{\rm { s.t.\;\; Constraints (11)-(36) }} $ | (42) |
| $ \sum\limits_{l \in L^{\text {down }}} \underline{\alpha}_{l}=\sum\limits_{l^{\prime} \in L^{\text {up }}} \bar{\beta}_{l^{\prime}}=\bar{n}^* $ | (43) |
| $ \sum\limits_{l \in L^{\text {down }}} \bar{\alpha}_l=\sum\limits_{l^{\prime} \in L^{\text {up }}} \underline{\beta}_{l^{\prime}}=\underline{n}^* $ | (44) |
where n* and n* are optimized solution obtained by solving F2. n* is the number of rolling stock coming from depot A, n* is the number of rolling stock coming from depot D.
4.3 Two-stage Solution AlgorithmBecause urban metro lines have many trains and stations, if the timetable and rolling stock circulation are optimized together, the structural complexity of the model will be greatly increased. Therefore, a two-stage solution algorithm is built. In the first stage, all the train services are assumed to be the full-length services. Model F1 is solved to find the optimized timetable of all train services. It is a simple MILP model which is easy to be solved with existing solvers. By solving model F1, the arrival and departure times of each train at each station are obtained, so that dsl, v, asl, v, dsl, v and asl, v are converted from variables to known parameters.
In the second stage, model F2 is firstly solved and the optimal values of the minimum number of rolling stocks (n* and n*) are obtained. The optimized results of F2 is taken as the inputs of model F3, which is then solved to maximize the number of full-length services under limited rolling stocks in order to provide more services to passengers at stations located between A and B (C and D, not including station B and C in Fig. 2).
5 Numerical Experiments 5.1 Solution PreparationThis numerical experiment runs in Windows 10 system environment, uses C# language and invokes Gurobi solver, and compiles in Visual Studio 2017 environment. Shanghai Metro Line 8 in China, as an example, is illustrated in Fig. 3. The whole line has a total of 30 stations, among which, station A (Shendu Highway) and station D (Shiguang Road) are close to depots. Stations A, B (Oriental Sports Center Station), C (Middle Yanji Road), and D support the turnaround operations. The train movement from A to D is the downward direction, and from D to A is the upward direction. In the downward direction, possible services include train services from A to D (A→D), A→C, B→D, and B→C. In the upward direction, possible services include train services D→A, C→A, D→B, and C→B. The train speed scale is divided into two kinds: the high speed scale is "ATO(Automatic Train Operation) normal", and the low speed scale is "ATO energy-saving".These are two different types of speed scales used by the ATO system in Shanghai Metro line 8. Other input parameters are described in Table 4.
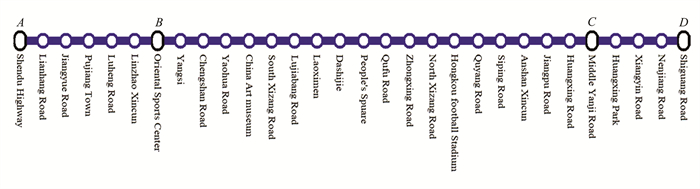
|
Fig.3 Shanghai metro line 8 |
| Table 4 Time parameters |
For comparisons, three scenarios are designed to analyze how the train operations can be influenced by the number of rolling stocks and the mixed usage of full-length and short-length services. In the first scenario (Scenario Ⅰ), it is assumed that all the train services are full-length services. So θ1, l and θ1, l are set to be 1. By solving F1 and F2 one after another, the minimum number of rolling stocks is obtained on condition that all trains execute full-length services. In the second scenario (Scenario Ⅱ), it is assumed that both full-length and short-length train services can be used. So that θ1, l and θ1, l are variables instead of given constants as in Scenario Ⅰ. By solving F1, F2, and F3 one after another, the minimum number of rolling stocks, as well as the maximum number of full-length services, is obtained. In the last scenario (Scenario Ⅲ), it is analyzed how the number of rolling stocks influences the line plans of train services. First, the optimized number of rolling stocks obtained in Scenario Ⅰ is higher than the value in Scenario Ⅱ. Because only the full-length services are used in Scenario Ⅰ, while the short-length services are allowed in Scenario Ⅱ, which means the rolling stocks in Scenario Ⅰ perform more services than in Scenario Ⅱ. Therefore more rolling stocks are needed. In Scenario Ⅲ, the optimized number of rolling stocks obtained in Scenario Ⅰ is taken as the upper bound, while the optimized number of rolling stocks obtained in Scenario Ⅱ is taken as the lower bound. Different numbers of rolling stocks within this range are then taken as the input of F3. By solving F3, the different optimized number of full-length services with the different number of rolling stocks are obtained.
5.2 Small Scale Numerical ExperimentTo verify the validity of the methodology presented in this paper, a small-scale numerical experiment was conducted to compare the Gurobi direct solution and the two-stage solution algorithm proposed in this paper. Scenario Ⅱ was solved. Only morning peak period is studied and the train speed scale is "ATO normal". The number of train service in the upward direction was equal to the number in the downward direction, and the number was gradually increased.Table 5 shows the efficiency comparison of the two methods. Fig. 4 shows the train timetable of 100 train services. It can be seen that with the increase of train service number, the solving time of the direct solution method increases exponentially. When train service number reaches 10, the direct solution method is not feasible. Two-stage solution algorithm proposed in this paper can stably address the actual needs of large quantities of data.
| Table 5 Efficiency comparison results of the two methods |

|
Fig.4 Train timetable (100 train services) |
5.3 Large Scale Numerical Experiment
To further verify the validity of two-stage solution algorithm proposed in this paper, the study period spans from 06:00 am to 0:00 am of the next day. The study period is divided into three periods, namely morning peak, flat peak, and evening peak. The speed scales in the morning peak and evening peak trains are "ATO normal", and the speed scale in the flat peak trains is "ATO energy saving". The number of train services of each period is referred to the existing train timetable: 310 trains in the upward and downward direction respectively, including 94/102/114 trains in the morning/ flat/ evening peaks in the downward direction, 90/105/115 trains in the morning/ flat/ evening peaks in the upward direction.Two-stage solution algorithm is used.
The optimization results of the three scenarios are reported in Table 6. Due to space limitations, only optimized rolling stock circulation of Scenario Ⅱ are presented in detail in Table 7. The corresponding train timetable of Scenario Ⅱ is shown in Figs. 5-7. In Table 7, rolling stocks A1-A29 come from the depot near Shengdu Highway station, rolling stocks B1-B34 come from the depot near Shiguang Road station. As for the train services, the odd numbers represent downward train services, and the even numbers represent upward train services.
| Table 6 Optimization results of the scenarios |
| Table 7 Rolling stock circulation (Scenario Ⅱ) |

|
Fig.5 Train timetable 6:00-12:00 (Scenario Ⅱ) |

|
Fig.6 Train timetable 12:00-18:00 (Scenario Ⅱ) |

|
Fig.7 Train timetable 18:00-0:00 (Scenario Ⅱ) |
Based on this result, the following conclusions can be drawn:
1) The number of rolling stocks has a significant impact on services.
In Scenario Ⅰ, the optimized minimum number of rolling stocks is 35 starting from station A and 36 starting from station D. In total, 71 rolling stocks are needed to run all full-length services. In Scenario Ⅱ, the optimized minimum number of rolling stocks is 29 starting from station A and 34 starting from station D. In total, 63 rolling stocks are needed. It shows that mixed use of short-length and full-length train services can optimize the use of the limited number of rolling stocks, enabling the running of as many train services as possible.
In Scenario Ⅲ, the given numbers of rolling stocks are within the range of [64, 70], the number of full-length services decreases with the decrease of the number of rolling stocks.
2) In Scenario Ⅱ, the proportion of full-length services is 79.8%, which is higher than in real-life. It is proved that the method proposed in this paper can significantly increase the proportion of full-length services by efficiently using the limited rolling stocks. The number of short-length services during the flat peak period is obviously lower than druing the morning and evening peak period. The train headway time during flat peak period is longer than during the morning and evening peak periods.So, appropriately increasing the train headway time is more conducive to reducing the number of short-length services, but will lead to a decrease in the total number of trains in a time-period. How to balance the relationship between headway time and service frequency needs further studies.
3) In Scenario Ⅱ, different rolling stocks service different number of train services. For example, rolling stock A8 services 15 train services (15-74-103-162-209-246-287-324-365-404-433-482-535-572-601). However, rolling stock B14 only services 3 train services (28-85-144). The average number of train services of one rolling stock served is around 9.5. The balance use of rolling stocks is not considered in the proposed model, i.e., the rolling stock is used equally, which can be further discussed in the future studies.
4) In Figs. 4-6, there is certain regularity in the train timetable. At the beginning of operation, the rolling stocks gradually exit depot and execute train services. At the end of the morning peak, a part of rolling stocks go back to depots, which gradually exit depots and execute train services at the beginning of the evening peak. But the number of rolling stocks leaving depots during the evening peak period is less than the number of rolling stocks entering depots after the morning peak. At the end of the operation day, all rolling stocks go back to depots. This regularity of rolling stocks entering and exiting depots is consistent with the reality.
6 ConclusionsA MINLP model is constructed to optimize the train timetable, rolling stock circulation and line plan. A two-stage solution algorithm is designed to solve the proposed model, which can significantly reduce the structural complexity of the model and accelerate the computational speed. The proposed method is adopted to optimize the timetable and rolling stock circulation of the whole day period of a metro line. The research results show that this method can make intensive rolling stock circulation and increase the number of full-length service trains. The minimum number of rolling stocks that can meet the normal train services of the whole day is 63, which can perform 495 full-length services out of all 620 services.
This study simplified the turn-around operations at stations, which can be further studied with considering more detailed turn-around operations. Moreover, the study focuses on the planning problem, how to adjust the rolling stock plan as well as the timetable in case of disruptions or disturbances should be considered in the future.
| [1] |
Xu R H, Li X, Chen J J. Optimization of routing mode on regional express rail. Urban Mass Transit, 2006, 9(5): 36-39. (  0) 0) |
| [2] |
Niu H, Chen M, Zhang M. Optimization theory and method of train operation scheme for urban rail transit. China Railway Science, 2011, 32(4): 128-133. DOI:10.1111/j.1365-2761.2010.01212.x (  0) 0) |
| [3] |
Xu D J, Mao B H, Chen S K, et al. Optimization of operation scheme for full-length and short-turn routings considering operation proportion. Journal of Traffic and Transportation Engineering, 2021, 21(2): 173-186. DOI:10.19818/j.cnki.1671-1637.2021.02.015 (  0) 0) |
| [4] |
Wang Y Y, Ni S Q. Optimization of train schedules of full-length & short-turn operation modes in urban rail transit. Journal of China Railway Society, 2013, 35(7): 1-8. (  0) 0) |
| [5] |
Dai C J, Li Y Z, Zhan Z S, et al. Optimization of train operation scheme for urban rail transit considering dynamic passenger demand and full-length and short-turn routing modes. China Railway Science, 2018, 39(2): 128-136. DOI:10.3969/j.issn.1001-4632.2018.02.16 (  0) 0) |
| [6] |
Cadarso L, Marín A. Improving robustness of rolling stock circulations in rapid transit networks. Computers & Operations Research, 2014, 51: 146-159. DOI:10.1016/j.cor.2014.05.007 (  0) 0) |
| [7] |
Giacco G L, Carillo D, D'Ariano A, et al. Short-term rail rolling stock rostering and maintenance scheduling. Transportation Research Procedia, 2014, 3: 651-659. DOI:10.1016/j.trpro.2014.10.044 (  0) 0) |
| [8] |
Cadarso L, Marin A, Maroti G. Integration of timetable planning and rolling stock in rapid transit networks. Annals of Operations Research, 2012, 199: 113-135. DOI:10.1007/s10479-011-0978-0 (  0) 0) |
| [9] |
Ying C S, Andy H F C, ChinK S. An actor-critic deep reinforcement learning approach for metro train scheduling with rolling stock circulation under stochastic demand. Transportation Research Part B: Methodological, 2020, 140: 210-235. DOI:10.1016/j.trb.2020.08.005 (  0) 0) |
| [10] |
Haahr J T, Wagenaar J C, Veelenturf L P, et al. A comparison of two exact methods for passenger railway rolling stock (re)scheduling. Transportation Research Part E: Logistics and Transportation Review, 2016, 91: 15-32. DOI:10.1016/j.tre.2016.03.019 (  0) 0) |
| [11] |
Jiang Z B, Xu R H, Wu Q, et al. Optimal model for using of transit unit based on shared-path rail transit route. Journal of Tongji University(Nature Science), 2014, 42(9): 1333-1431. DOI:10.3969/j.issn.0253-374x.2014.09.005 (  0) 0) |
| [12] |
Lusby R M, Haahr J T, Larsen J, et al. A branch-and-price algorithm for railway rolling stock rescheduling. Transportation Research Part B: Methodological, 2017, 99: 228-250. DOI:10.1016/j.trb.2017.03.003 (  0) 0) |
| [13] |
Yue Y, Han J, Wang S, et al. Integrated train timetabling and rolling stock scheduling model based on time-dependent demand for urban rail transit. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(10): 856-873. DOI:10.1111/mice.12300 (  0) 0) |
| [14] |
Xu R H, Chen J J, Du S M. Study on carrying capacity and use of rolling stock with multi-routing in urban rail transit. Journal of the China Railway Society, 2005, 27(4): 6-10. (  0) 0) |
| [15] |
Wang Y, D'ariano A, Yin J, et al. Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line. Transportation Research Part B: Methodological, 2018, 118: 193-227. DOI:10.1016/j.trb.2018.10.006 (  0) 0) |
| [16] |
Liu R M, Li S K, Yang L X. Collaborative optimization for metro train scheduling and train connections combined with passenger flow control strategy. Omega, 2020, 90: 101990. DOI:10.1016/j.omega.2018.10.020 (  0) 0) |
| [17] |
Wang Y H, Tang T, Ning B, et al. Integrated optimization of regular train schedule and train circulation plan for urban rail transit lines. Transportation Research Part E: Logistics and Transportation Review, 2017, 105: 83-104. DOI:10.1016/j.tre.2017.06.001 (  0) 0) |
| [18] |
Zhang M, Wang Y H, Su S, et al. A Short turning strategy for train scheduling optimization in an urban rail transit line: The case of Beijing subway line 4. Journal of Advanced Transportation, 2018(7): 1-19. DOI:10.1155/2018/5367295 (  0) 0) |
| [19] |
Wang Y H, Liao Z B, Tang T, et al. Train scheduling and circulation planning in urban rail transit lines. Control Engineering Practice, 2017, 61: 112-123. DOI:10.1016/j.conengprac.2017.02.006 (  0) 0) |
| [20] |
Peeters M, Kroon L. Circulation of railway rolling stock: a branch-and-price approach. Computers & Operations Research, 2008, 35(2): 538-556. DOI:10.1016/j.cor.2006.03.019 (  0) 0) |
| [21] |
Ying C S, Andy H F C, Chin K S. An actor-critic deep reinforcement learning approach for metro train scheduling with rolling stock circulation under stochastic demand. Transportation Research Part B: Methodological, 2020, 140: 210-235. DOI:10.1016/j.trb.2020.08.005 (  0) 0) |
 2024, Vol. 31
2024, Vol. 31


