2. 斯达玻璃钢有限公司,哈尔滨 150001;
3. 中国石油吉林油田公司 勘察设计院,吉林 松原 138000
2. Star Fiberglass Harbin Co. Ltd, Harbin 150088, China;
3. Survey & Design Institute, China National Petroleum Corporation Jilin Oilfield, Songyuan 138000, China
CO2与水交替注入驱油是一种高效环保的驱油方法[1-2],不但可以提高原油采收率,还可以填埋大量含CO2工业废气,减少了温室气体的排放,因而具有非常好的发展前景.通常,CO2是在超临界状态注入井下的[3-4],而超临界CO2(sc-CO2)扩散系数为液体的近百倍,具有较强的溶解能力[5-6].CO2溶于水后形成的H2CO3对钢铁及水泥环都有很强的腐蚀性[7],易导致管道和设备产生早期腐蚀失效,甚至造成生产油、套管的腐蚀断裂,大大缩短了油气井的生产寿命.
玻璃增强环氧树脂复合材料(GFRP)具有优良耐腐蚀性能,因而大量应用于石油化工、电力、污水、冶金等行业[8].GFRP受成型工艺和材料属性的限制,其表面和内部含有一定数量的孔隙、缺陷、少量小分子物质和填料,因而在输送sc-CO2时存在介质向材料内部的渗透和扩散问题.目前,国内外关于CO2腐蚀的研究多集中在金属材料,CO2对高聚物材料的腐蚀研究很少.
计算流体力学是对流体流动和传热等相关物理现象乃至化学反应系统进行分析的一门学科.通过流体力学模拟流体运动随时间变化的趋势,结合实际工程参数,并引入时间加速倍数,从而得到实际工程中的渗透深度随时间的关系,进而估算GFRP的剩余强度和剩余寿命,具有重要的理论意义与实际应用价值.
本文建立了sc-CO2对GFRP管道的多孔介质渗透扩散模型,运用计算机流体力学软件FLUENT进行数值模拟,研究渗透深度随时间变化的规律,以及不同压强和温度对sc-CO2在GFRP中的渗透和扩散的影响,讨论GFRP在输送sc-CO2中的物理腐蚀作用.
1 sc-CO2对GFRP的渗透模型孔隙是纤维增强聚合物基型复合材料的常见缺陷之一,主要来源于制造过程中“包陷”在纤维和树脂中的空气,这类孔隙尺寸较大,数量较少,位置则属于随机分布.另外,树脂固化和后加工的过程中,有机溶剂组分等小分子挥发会形成微小孔隙[9],这些孔隙的数量基数较大,尺寸较小,均匀分布在管材的表面和内部.处于液相或气相中的高聚物材料,渗透作用主要表现在两方面.一方面是腐蚀介质由高浓度区域向高聚物材料内部的缺陷区域扩散迁移,另一方面是高聚物内部的可溶性小分子和腐蚀产物向环境介质中的迁移过程[10].
本文选用胺类固化GFRP高压管作为研究对象,管壁内存在的孔隙直径为0.5~3 μm(如图 1所示),通过超声波C扫描进行无损检测得到其孔隙率为3%,管材基本参数如表 1所示.

|
图 1 GFRP内表面SEM照片 |
| 表 1 胺类固化GFRP高压管道参数 |
综合GFRP管道内孔隙和缺陷特点,文中采用多孔介质模型,忽略孔隙的尺寸差别,以试验测得的孔隙率3%作为基准量,假设其均匀分布在管材的表面和内部,通过控制孔隙的开放度得到较为理想的渗透扩散模型.设定管道区域为sc-CO2流场区域,对管道的参数设定主要为管道对sc-CO2的粘性阻力系数以及惯性阻力系数.
多孔介质模型采用经验公式定义流动阻力[11],本质就是在流体动量方程中增加了1个代表能量消耗的源项Si,其表达式为
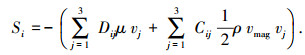
|
(1) |
式中:Dij和Cij为给定矩阵系数;Si为第i个(x、y或z方向)动量方程的源项;μ为粘度,Pa·s;v为速度,m/s.
对于简单、均匀的多孔介质,可使用数学模型

|
(2) |
式中:α为多孔介质的渗透性;1/α为粘性阻力系数;C2为惯性阻力系数;ρ为密度,kg/m3.
利用半经验公式Ergun方程来确定1/α和C2:
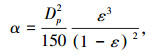
|
(3) |
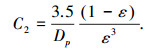
|
(4) |
式中:Dp为孔隙平均直径,m;ε为孔隙率.
由式(3)及式(4)计算GFRP管道的粘性阻力系数1/α以及惯性阻力系数C2.
2 sc-CO2对GFRP的渗透数值模拟在给定的压强下,流体的密度、导热系数、粘度均随温度的升高而降低,并在临界温度附近大幅下降,超过临界点后则趋于平缓.在给定的温度下,流体的密度、导热系数以及粘度均随压强的升高而升高[12].本文选取3个温度梯度40、60和80 ℃,3个压强梯度8、10和12 MPa,分别研究温度和压强对CO2渗透性的影响.
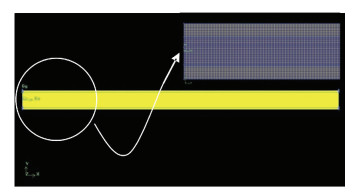
GFRP管道沿轴线的剖面图,采用收敛性较好的2D模型对剖面的渗透情况进行模拟,网格划分及其局部放大视图如图 2所示.
|
图 2 GFRP管2D模型网格划分及局部放大视图 |
选用基于压力的分离式求解器,压力速度耦合方法则采用标准SIMPLE方法.管内流场选用目前使用最广泛的标准k-ε双方程模型来模拟.
入口边界条件:采用速度入口边界条件,入口介质为超临界CO2,设定入口截面法向速度为0.5 m/s.湍流模型选用Intensity and Length Scale,湍流密度5%,湍流直径0.001 m.
出口边界条件:采用压力出口边界条件,湍流模型采用与入口边界一样的设置.
管道壁边界条件:采用多孔介质边界条件,孔隙率设定3%,平均孔隙直径设定为0.5 μm.粘性阻力系数与惯性阻力系数由式(3)和式(4)计算得到,其余保持缺省设置.
3 结果及讨论 3.1 渗透行为随时间的变化规律在操作压强8 MPa、操作温度60 ℃的环境下,采用降低粘性阻力系数与惯性阻力系数数量级的方法加速渗透.将实际管道的平均孔隙直径以及孔隙率代入式(3)和式(4),得到实际管道的粘性阻力系数及惯性阻力系数,通过同时降低或增加数量级的方法进行模拟,3组模拟操作系数设置如表 2所示,其对应的渗透深度随时间变化曲线如图 3所示.假设渗透完成的时间为t,渗透深度趋势对比如图 4所示.
| 表 2 粘性阻力系数与惯性阻力系数设置 |
|
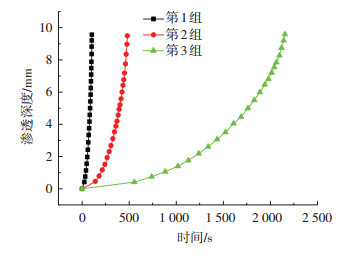
图 3 3组阻力系数下渗透深度随时间变化曲线 |
|
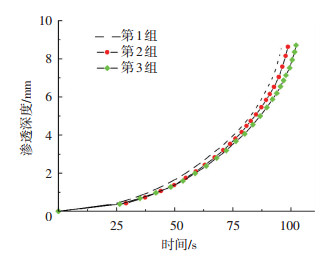
图 4 3组阻力系数下渗透深度趋势图 |
由图 3可知:随着粘性阻力系数和惯性阻力系数的同时增大,渗透深度所需的时间大大增加,2个系数同时增加1个数量级,sc-CO2渗透至相同深度所需时间相差数倍,并最终都渗透至整个管层结构.在实际过程中,渗透不是无限进行的,随着渗透深度的增加,粘性阻力系数和惯性阻力系数都是增加的,因此模拟曲线的后期趋势与实际渗透有一定差距,还需要进一步的研究.
由图 4可知,倘若整个渗透过程所用相对时间为100%,在对应的相对时间内,3组阻力系数设置下sc-CO2在GFRP中的渗透深度变化趋势大致相同.这也说明不同渗透阻力下,sc-CO2的渗透行为并没有本质的差别,都是以润湿-填充的形式进行的,其差别主要是整个过程中的进行速度.
3.2 温度对渗透行为的影响温度是影响分子运动的重要因素,随着温度升高,小分子与大分子运动都会加剧[13],因而研究温度对渗透行为的影响具有重要意义.选择操作压强8 MPa,操作温度选择40、60、80 ℃分别对3种条件下的sc-CO2在GFRP中的渗透行为进行模拟,介质的参数设置与第2组中的管道参数相同,所得到对应的渗透深度随时间的变化曲线如图 5所示.
|
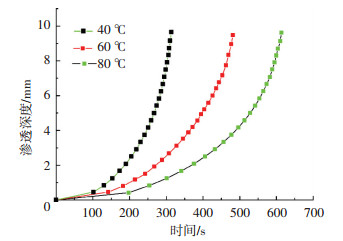
图 5 不同温度下渗透深度随时间变化曲线 |
由图 5可见:相同操作压下,温度越高,渗透至相同深度所用时间越长.由于在8 MPa压强下,sc-CO2的密度随温度的升高而降低,尽管分子运动更活跃,但高浓度向低浓度迁移的驱动力减小.另外,氧树脂作为一种高分子化合物,在受到应力的作用时,会产生大分子链段的取向和重排[14].在操作压强为8 MPa时,操作温度从40 ℃升高到80 ℃的过程中,环氧树脂分子链段运动更加活跃,并在环向应力的作用下产生链段取向和重排,扩大了树脂基体的结晶区,一定程度上阻碍了sc-CO2分子的渗透和扩散,从而造成了sc-CO2渗透速率的降低.
3.3 压强对渗透速率的影响压强对渗透行为的影响也是显著的,压力是超临界流体运动的主要动力.另外,sc-CO2的密度的增加,也是促使sc-CO2向孔隙中渗透扩散的驱动力.选择操作温度为60 ℃,操作压强分别为8、10、12 MPa,采用第2组中管道参数分别对不同压强条件下sc-CO2在GFRP中的渗透行为进行模拟,对应的渗透深度与时间的关系曲线如图 6所示.
|
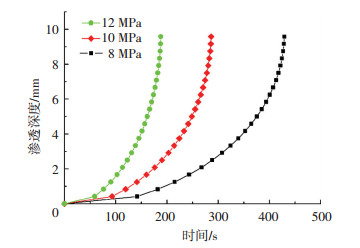
图 6 不同压强下渗透深度随时间变化曲线 |
由图 6可见:相同温度下,操作压强越高,渗透至相同深度所用时间越短,当压强大于CO2临界压强时,随压强的升高CO2渗透速率明显升高;随着操作压强的增大,压力对超sc-CO2产生更大的推进作用,使sc-CO2更容易通过孔隙进行渗透和扩散[15].同时,压强的增大使得sc-CO2的密度增大,导致流体由高浓度区域更快的向环氧树脂内部的缺陷区域扩散迁移,从而加快了渗透和扩散的速度.另外,压强的增大导致基体链段松弛时间缩短,使链段运动的活化能降低,压力增加到一定程度,迫使材料产生强迫高弹形变,有助于超临界状态CO2向GFRP深层的渗透.
综上所述,FLUENT模拟的结果具有一定的参考意义,可以通过渗透深度随时间的趋势,结合GFRP在实际使用过程中的工程参数,并引入时间加速倍数,从而得到实际工程中的渗透深度随时间的关系,判断服役中GFRP管材的渗透深度,进而通过渗透深度与强度的关系估算GFRP的剩余强度,得到管材的剩余寿命.
4 结论1) 不同渗透阻力下,sc-CO2在GFRP中的渗透速度相差较大,渗透深度的变化趋势则基本一致,渗透过程只有速度的差别,没有本质的差别.结合实际工程数据,可以得到实际工程中的渗透深度与时间的关系曲线.
2) sc-CO2在GFRP中的渗透速度随着温度的升高而降低,这是由于sc-CO2随温度的升高而密度减小,降低了sc-CO2从高浓度向低浓度迁移的趋势.
3) 压力是介质运动的动力,因而sc-CO2在GFRP中的渗透速度随着压强的升高而升高;另外,压强的升高导致sc-CO2密度升高,增加了sc-CO2从高浓度向低浓度迁移的趋势.
| [1] |
乔红军, 任晓娟, 闫凤平, 等. 低渗透储层水气交替注入方式室内试验研究[J]. 石油天然气学报, 2013, 35(7): 114–117.
QIAO Hongjun, REN Xiaojuan, YAN Fengping, et al. Experimental study of low permeability reservoir with water alternate gas injection method[J]. Journal of Oil and Gas Technology, 2013, 35(7): 114–117. |
| [2] | KERMANI M B, MORSHED A B. Carbon dioxide corrosion in oil and gas production-a compendium[J]. Corrosion, 2003, 59(8): 659–683. DOI: 10.5006/1.3277596 |
| [3] |
高云丛, 赵密福, 王建波, 等. 特低渗油藏CO2非混相驱生产特征与气窜规律[J]. 石油勘探与开发, 2014, 41(1): 79–85.
GAO Yuncong, ZHAO Mifu, WANG Jianbo, et al. Performance and gas breakthrough during CO2 immiscible flooding in ultra-low permeability reservoirs[J]. Petroleum Exploration and Development, 2014, 41(1): 79–85. DOI: 10.11698/PED.2014.01.10 |
| [4] | QAMAR M M, ISLAM M R. CO2 injection in the weyburn field of Canada: optimization of enhanced oil recovery and greenhouse gas storage with horizontal wells[C]//SPE/DOE Improved Oil Recovery Symposium. Oklahoma: [s. n.], 2000: 1-17. |
| [5] | LIU B, WONG-FOY A G, MATZGER A J. Rapid and enhanced activation of microporous coordination polymers by flowing supercritical CO2[J]. Chem Commun, 2013, 49(14): 1419–1421. DOI: 10.1039/c2cc37793d |
| [6] |
王世杰. 原油含水率对油气管材超临界CO2腐蚀行为的影响[J]. 腐蚀科学与防护技术, 2015, 27(1): 73–77.
WANG Shijie. Effect of water content of crude oil on corrosion behavior of oil and gas tubular goods steel in supercritical CO2 system[J]. Corrosion Science and Protection Technology, 2015, 27(1): 73–77. DOI: 10.11903/1002.6495.2014.053 |
| [7] |
李天成. 榆济天然气管道内腐蚀原因[J]. 腐蚀与防护, 2014, 35(3): 282–285.
LI Tiancheng. Internal corrosion causes of Yu-Ji natural gas transmission pipeline[J]. Corrosion and Protection, 2014, 35(3): 282–285. |
| [8] | 宋文娟. 玻纤增强环氧树脂复合材料耐海水腐蚀行为与寿命预测[D]. 哈尔滨: 哈尔滨工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015021890.htm |
| [9] |
张阿樱, 张东兴, 李地红, 等. 碳纤维/环氧树脂层压板的孔隙问题[J]. 宇航材料工艺, 2011(3): 16–19.
ZHANG Aying, ZHANG Dongxing, LI Dihong, et al. Void of carbon fiber reinforced epoxy laminates[J]. Aerospace Materials & Technology, 2011(3): 16–19. |
| [10] | GRUNLAN J C, MEHRABI A R, BANNON M V, et al. Water-based single-walled-nanotube-filled polymer composite with an exceptionally low percolation threshold[J]. Advanced Materials, 2004, 16(2): 150–153. DOI: 10.1002/(ISSN)1521-4095 |
| [11] | 李进良, 李承曦, 胡仁喜, 等. 精通FLUENT流场分析[M]. 北京: 化学工业出版社, 2009: 12-17. |
| [12] | LEMMON E W, Mc LINDEN M O, FRIEND D G. Thermophysical Properties of Fluid Systems[J]. NIST Chemistry Webbook, NIST Standard Reference Database, 2005: 69. |
| [13] |
赵培仲, 王源升, 朱金华, 等. 聚氨酯弹性体的高弹模量对温度的依赖性[J]. 高分子材料科学与工程, 2008, 24(4): 89–92.
ZHAO Peizhong, WANG Yuansheng, ZHU Jinhua, et al. Temperature dependence of plateau modulus of polyurethane elastome[J]. Materials Science and Engineering, 2008, 24(4): 89–92. |
| [14] | 王彬. 聚丙烯腈纤维取向结构对热稳定化反应的影响[D]. 北京: 北京化工大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10010-1012414824.htm |
| [15] |
王静, 李军建, 吴启鹏. 阻隔材料的气体渗透率[J]. 强激光与粒子束, 2012, 24(7): 1619–1623.
WANG Jing, LI Junjian, WU Qipeng. Gas permeability of barrier materials[J]. High Power Laser and Particle Beams, 2012, 24(7): 1619–1623. |
 2016, Vol. 24
2016, Vol. 24




