2.哈尔滨工业大学 材料科学与工程学院,哈尔滨150001
2.School of Materials Science and Engineering,Harbin Institute of Technology,Harbin 150001,China
热塑性复合材料是以玻璃纤维、碳纤维、芳纶纤维及其他材料增强的各种热塑性树脂的总称,具有密度小、强度高、可设计性强、成型加工率高等特点,广泛应用于汽车、航空航天、机械、电子电气等领域[1-3].采用纤维增强的热塑性塑料管极大地提高了复合管道的承压强度,降低了生产成本.例如,芳纶纤维增强复合管可在压力10 MPa下输送原油和酸性天然气,且考虑弯头、施工、运行等方面后的综合费用比钢管的大约低25%[4-6].玻璃纤维抗拉强度为1 000~3 000 MPa,虽相较于碳纤维、芳纶纤维低,但其材料来源丰富、价格低,应用前景广阔,使得连续玻纤增强复合带的研制成为了当前的技术热点[7-9].
目前,美国的Ticona、PMC Baycomp以及荷兰的TenCate公司,掌握了连续玻纤增强复合带的生产工艺.一些研究人员对纤维增强复合带的制备和生产工艺进行了研究,并给出了层铺结构的复合带弹性性能参数计算方法,但对于束状纤维结构的复合带弹性性能参数的研究较少[10-12],未见有可供直接用于计算的公式或算法.
本文在山东科技大学王庆昭教授课题组成功开发出连续玻纤/PE增强复合带(以下简称复合带)工艺与制品的基础上,采用理论公式、有限元模拟和实验手段求解了复合带的整体弹性参数,为复合带的设计及力学分析提供了必要的数据.
1 连续玻纤增强复合带模型 1.1 几何模型本文研究的复合带是将连续玻纤进行偶联处理后与PE复合而成的带,结构如图 1所示.复合带厚度0.45 mm,玻纤截面为矩形,尺寸为3 mm×0.222 mm,玻纤束位于PE中间,相邻玻纤束中心距为4 mm.玻纤所占的体积分数对复合带的性能影响较大,其体积分数越大,复合带强度越高,但PE所占比例过少,玻纤的粘结及包裹效果会下降,同时会造成加工困难,所以,合理设计玻纤和PE所占的比例分数具有重要的意义[13].

|
图 1 连续玻纤增强复合带模型 |
复合带的成型工艺及材料结构状态较复杂,很难用数学模型对其进行精确描述.为了简化计算,在复合带弹性性能参数求解过程中对其结构及材料作如下假设:1) PE和玻璃纤维均为连续、均匀、各向同性的材料,忽略裂纹、孔隙等缺陷,且在复合前后PE及玻璃纤维的性能没有变化;2) 玻璃纤维在PE中分布均匀;3) 玻璃纤维和PE在界面处应变连续,不发生相对滑移;4) 玻璃纤维和PE均处于线弹性状态、小变形,且无初应力.
2 弹性参数求解 2.1 公式法求解弹性参数目前,关于复合带的研究大多以钢丝增强为主,以玻纤为增强体的复合材料的研究较少.郑津洋等[14]将钢丝缠绕增强塑料复合管假设为变形连续的内层、复合层、外层3层结构组成,对单层板进行了模型的简化,在保持各组分面积不变的条件下将圆形截面转化为正方形截面,然后采用串并联模型求得单层板的弹性参数.此文献中推导出了单层板弹性参数的求解公式,用以指导计算复合层的弹性参数,进而推导出各层界面上接触压力与轴向力的方程组,最后得到复合管各层的应力及应变计算公式.
将连续玻纤与PE复合,提高了PE在玻纤方向的强度,使得复合带具有各向异性.参考了文献[14]中复合管单层板弹性参数的分析方法,复合带的力学模型如图 1所示.其中,a表示单束玻纤的厚度,b表示单束玻纤的宽度,B/2表示相邻玻纤束的中心距.
图 2所示为复合带模型中的代表性体积单元,其长为相邻玻纤束中心距一半B/2,宽为复合带厚度一半A/2.应用公式求解复合带的弹性参数,如下所述.
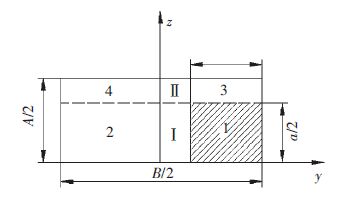
|
图 2 复合带的代表性体积单元 |
弹性模量求解公式:
| ${E_x} = {E_2}xx' + {E_1}\left( {1 - xx'} \right),$ | (1) |
| ${E_y} = {{\left( {{E_1} - {E_2}} \right){E_1}xx'} \over {{E_1}x + {E_2}y}} + {E_1},$ | (2) |
| ${E_z} = {{\left( {{E_1} - {E_2}} \right){E_1}xx'} \over {{E_1}x' + {E_2}y}} + {E_1}.$ | (3) |
其中:x、y分别表示I区域中玻纤、PE所占比例;x'、y'分别表示代表性体积单元中I、II区域所占比例.
泊松比求解公式:
| ${\mu _{xy}} = {{xy'{\mu _1}{E_1} + \left( {yy'{\mu _1} + x'y{\mu _1} + xx'{\mu _2}} \right){E_1}} \over {\left( {x' + yy'} \right){E_2} + xy'{E_1}}},$ | (4) |
| ${\mu _{xz}} = {{{\mu _2}{E_2}xx' + {\mu _1}{E_1}x'y} \over {\left( {{\mu _2}x + {\mu _1}y} \right)y' + {\mu _1}x'}} + {\mu _1}y',$ | (5) |
| ${\mu _{zy}} = {{{\mu _1}\left( {{\mu _2}x + {\mu _1}y} \right)} \over {\left( {{\mu _2}x + {\mu _1}y} \right)y' + {\mu _1}x'}}.$ | (6) |
剪切弹性模量求解公式:
| ${G_{xy}} = {{{G_1}{G_2}x'} \over {\left( {{G_1}x} \right) + {G_2}y}}{G_1}y',$ | (7) |
| ${G_{xz}} = {{{G_1}\left( {{G_2}x + {G_1}y} \right)} \over {{G_1}x' + {G_2}xy' + {G_1}yy'}},$ | (8) |
| ${G_{zy}} = {{{G_1}{G_2}} \over {{G_1}xx' + {G_2}\left( {1 - xx'} \right)}},$ | (9) |
式中:Ex、Ey、Ez为复合带的各向弹性模量,MPa;μxy、μxz、μzy为复合带的各向泊松比;Gxy、Gxz、Gzy为复合带的各向剪切模量,MPa;E1、E2分别表示PE、玻纤的弹性模量,MPa;μ1、μ2分别表示PE、玻纤的泊松比;G1、G2分别表示PE、玻纤的剪切模量,MPa.
模型除玻纤与钢丝在材料性能方面不同外,还有2点不同:1) 玻纤束为方形,而文献[14]中是将圆形的钢丝截面近似为方形;2) 复合带在受到沿玻纤长度方向的拉力时,玻纤束在拉力的方向上承担主要的力,而在垂直于玻纤方向,当玻纤束受到拉应力时,玻纤束所能承担的力与纤维之间的粘接强度有关.复合带有关计算参数见表 1.
| 表 1 材料参数 |
把玻纤体积分数为37%的复合带材料参数及有关结构参数代入式(1) ~(9) ,得到复合带的弹性参数,见表 2.
| 表 2 复合带弹性参数 |
应用有限元法[15]对复合带整体结构进行模拟,可以得到加载后的变形量及应力分布,不但可用来指导复合带的设计,并且可以求解复合带的弹性参数,为复合缠绕管道的设计计算提供参数.
基于公式法中复合带的结构特点及假设,建立玻纤和PE的几何模型并划分网格,对两者结合处进行位移耦合约束,建立了复合带的有限元模型如图 3所示.其中,取玻纤的长度方向为x方向,面内垂直玻纤方向为y方向,玻纤复合带的法线方向为z方向.选用Solid45单元,模拟中需定义材料参数见表 1.
|
图 3 复合带模型 |
在施加边界条件时,将模型一端固定,一端施加21.6 MPa的均布载荷.由于玻纤和PE是作为2个体分别进行的建模,故需在x方向进行位移耦合约束,使得玻纤和PE作为一个整体来承担单向拉力.
由Ansys中的应力-应变关系及广义胡克定律[17]可推导出复合带在x方向的弹性模量计算公式
| ${E_x} = {{{\sigma _x} - {\mu _{xy}}{\sigma _y} - {\mu _{xz}}{\sigma _z}} \over {{\varepsilon _x}}}.$ | (10) |
式中:σx、σy、σz 为复合带的各向应力,MPa; μxy、μxz为复合带的各向泊松比;εx为复合带玻纤长度方向应变.有限元分析结果如图 4和图 5所示.

|
图 4 复合带的等效应力云图 |
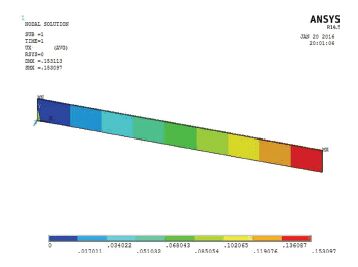
|
图 5 复合带x方向位移云图 |
由图 4可知,复合带中PE受到的最大应力为8.2 MPa,玻纤受到的最大应力为54.12 MPa,说明复合带在单向拉力的状态下,玻纤承担主要的应力,约为87%.
由图 5可知,复合带在x方向的最大位移为0.153 mm,由于复合带一端固定,一端施加单向均布载荷及x方向的位移耦合约束,模型受到的是单向拉力,故模型在x方向的最大位移即为模型在沿玻纤方向的整体位移.
将模拟结果代入式(10) ,计算得到复合带沿玻纤长度方向的弹性模量为14 117 MPa.
3 拉伸实验法采用万能电子材料实验机对复合带分别进行了纵向拉伸实验和横向拉伸实验.分别制备复合带的纵向和横向拉伸试样,试样见图 6.

|
图 6 复合带试样 |
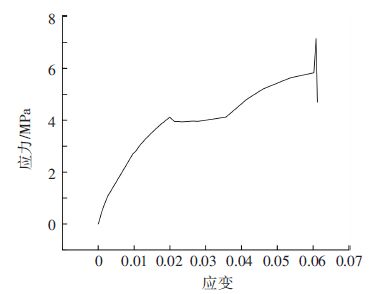
通过实验,分别获得了纵向和横向的拉伸实验曲线,如图 7、图 8所示.
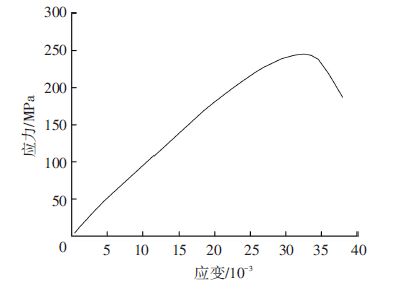
|
图 7 纵向拉伸实验曲线 |
|
图 8 横向拉伸实验曲线 |
由胡克定律得到弹性模量的推导公式
| $E = {{\Delta F} \over {A\left( {{\varepsilon _2} - {\varepsilon _1}} \right)}}.$ | (11) |
式中:ΔF为复合带所受到的单向拉力之差,N;A为复合带的横截面积,mm2;ε1,ε2分别为复合带所受单向拉力对应的应变.
将实验及测量所得数据代入式(11) ,得到复合带的弹性参数为Ex=11 236.93 MPa.
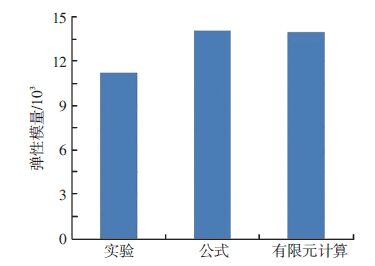
4 讨论分析实验数据与公式计算和有限元计算所得数据进行对比分析,如图 9所示.
|
图 9 玻纤长度方向的弹性模量 |
由图 9可知,通过实验、公式和模拟计算所得玻纤长度方向的弹性模量分别为11 236.93、14 117和14 021 MPa.对比以上数据发现,公式计算结果与模拟结果基本吻合,两者比实验值偏大,约25%.
理论值、数值解与实验值存在差异主要是由以下原因引起:在应用理论公式和有限元方法计算时采用了假设条件,材料为理想状态,而实际生产中玻璃纤维必然会有一定程度的损伤;同时,玻纤和聚乙烯结合处的界面状态也无法到达绝对的理想状态.实际生产中,材料的状态及性能往往与数学描述存在偏差,只能通过提高加工工艺水平尽可能接近理论值.
5 结 论1) 在建立复合带物理模型的基础上,提出了进行力学计算的假设条件,分析了复合带拉伸过程力学特点,推导出了弹性参数计算公式.此公式可应用于求解方形连续纤维增强复合带的弹性参数,且公式法操作简单省时.
2) 建立了复合带在单向拉伸状态下的有限元模型,并对玻纤与PE进行了耦合处理,所得复合带沿玻纤长度方向的弹性模量与公式法求解结果吻合很好,有限元法和公式法都可用来获得方形连续玻纤增强复合带的弹性参数.
3) 应用拉伸实验获得了复合带沿玻纤长度方向与其垂直方向(带平面内)的弹性模量(Ex和Ey),理论解和数值解比实验值偏大约29%.该数据可在以后复合带的设计中作为安全系数的推荐值.公式法与数值方法均在假设理想状态下求解而实际工艺很难达到理想状态,由此带来的误差可以进一步提高复合带得加工工艺和实验测量精度来减小.
| [1] |
何建明, 王选伦, 李又兵, 等. 长玻纤增强聚丙烯复合材料力学性能的研究[J]. 橡塑技术与装备, 2014, 40 (24) : 29 –31.
HE Jianming, WANG Xuanlun, LI Youbing, et al. Study of the mechanical properties of polypropylene long glass fiber reinforced composites[J]. Plastics Technology and Equipment, 2014, 40 (24) : 29 –31.
( 0) 0)
|
| [2] |
代少俊. 高性能纤维复合材料. 上海: 华东理工大学出版社, 2013 .
( 0) 0)
|
| [3] |
沈尔明, 王志宏, 滕佰秋, 等. 连续纤维增强复合材料在民用航空发动机上的应用[J]. 航空发动机, 2013, 39 (2) : 90 –94.
SHEN Erming, WANG Zhihong, TENG Baiqiu, et al. Application of fiber reinforced composites in civil aeroengines[J]. Aeroengine, 2013, 39 (2) : 90 –94.
( 0) 0)
|
| [4] |
XIA M, Takayanagi H, Kemmochi K. Analysis of multi-layered filament-wound composite pipes under internal pressure[J]. Composite Structure, 2001, 53 : 483 –491.
DOI: 10.1016/S0263-8223(01)00061-7 ( 0) 0)
|
| [5] |
张越, 樊新民, 孔德仁. 复合层合管力学模型的研究[J]. 南京理工大学学报, 1999, 23 (5) : 446 –449.
ZHANG Yue, FAN Xinmin, KONG Deren. Study on the mechanics model of multi-layered tube[J]. Journal of Nanjing University of Science and Technology, 1999, 23 (5) : 446 –449.
( 0) 0)
|
| [6] |
WITHERS G J, YU Y, KHABASHESKU V N, et al. Improved mechanical properties of an epoxy glass-fiber composite reinforced with surface organomodified nanoclays[J]. Composites Part B Engineering, 2015 : 175 –182.
( 0) 0)
|
| [7] |
张兴邦. 连续玻璃纤维增强PE复合带的研制[D]. 青岛: 山东科技大学, 2014.
( 0) 0)
|
| [8] |
OZKAN C, KARSLI N G, AYTAC A, et al. Short carbon fiber reinforced polycarbonate composites: Effects of different sizing materials[J]. Composites Part B, 2014, 62 (3) : 230 –235.
( 0) 0)
|
| [9] |
张如良, 刘赟, 黄玉东, 等. 碳纤维复合材料界面反应动力学分析[J]. 哈尔滨工业大学学报, 2013, 45 (10) : 69 –74.
ZHANG Ruliang, LIU Yun, HUANG Yudong, et al. Interfacial reaction kinetics of carbon fiber composite[J]. Journal of Harbin Institute of Technology, 2013, 45 (10) : 69 –74.
( 0) 0)
|
| [10] |
方立. 连续纤维热塑性复合材料制备及其性能的研究[D]. 上海: 华东理工大学, 2012.
( 0) 0)
|
| [11] |
LIU Dong, ZHU Yingdan, DING Jianping, et al. Experimental investigation of carbon fiber reinforced poly(phenylene sulfide) composites prepared using a double-belt press[J]. Composites Part B, 2015, 77 : 363 –370.
DOI: 10.1016/j.compositesb.2015.03.062 ( 0) 0)
|
| [12] |
南建举, 邓丽莉, 于俊荣, 等. HDPE基芳纶增强复合带的制备[J]. 高科技纤维与应用, 2010, 35 (5) : 32 –36.
NAN Jianju, DENG Lili, YU Junrong, et al. Study on the preparation of HDPE-based resin matrixed aramid fiber-reinforced composited tape[J]. Hi-Tech Fiber and Application, 2010, 35 (5) : 32 –36.
( 0) 0)
|
| [13] |
SRISUWAN S, PRASOETSOPHA N, SUPPAKARN N, et al. The effects of alkalized and silanized woven sisal fibers on mechanical properties of natural rubber modified epoxy resin[J]. Energy Procedia, 2014, 56 : 19 –25.
DOI: 10.1016/j.egypro.2014.07.127 ( 0) 0)
|
| [14] |
郑津洋, 林秀峰, 卢玉斌, 等. 钢丝缠绕增强塑料复合管的应力分析[J]. 中国塑料, 2006, 20 (7) : 56 –61.
ZHENG Jinyang, LIN Xiufeng, LU Yubin, et al. Stress analysis of plastic pipe reinforced by cross helically winding steel wire[J]. China Plastics, 2006, 20 (7) : 56 –61.
( 0) 0)
|
| [15] |
付敏, 林松, 陈亮, 等. 纤维缠绕复合材料气瓶内衬的屈曲分析[J]. 材料科学与工艺, 2015, 23 (2) : 86 –90.
FU Min, LIN Song, CHEN Liang, et al. Liner buckling analysis of composite overwrapped pressure vessel[J]. Materials Science and Technology, 2015, 23 (2) : 86 –90.
( 0) 0)
|
| [16] |
杨桂通. 弹塑性力学引论. 北京: 清华大学出版社, 2004 .
( 0) 0)
|
 2016, Vol. 24
2016, Vol. 24


