虎头结构(绞座)为装载机前车架与后车架的连接部分,起着转动枢纽的作用,是一个关键的焊接结构.虎头结构位于后车架前端,在焊接生产过程中最突出的问题就是存在较大的焊接变形,焊接变形将会影响焊接结构的正常装配及使用[1-7].在实际生产中,预测和控制焊接变形主要依靠经验和大量的试验,且在焊接结构出现焊接变形超出设计尺寸要求时还需要采取矫正措施,这样做既增加了成本又会改变焊接结构残余应力的分布情况[8-12].焊接变形受焊接顺序影响很大,因此合理地优化焊接顺序可以良好地控制焊接变形,同时可以降低成本[13-16].
随着有限元数值模拟仿真技术的快速发展,越来越多国内外学者利用其预测复杂结构件的焊接变形[17-25].文中使用有限元分析软件MARC,以装载机后车架的虎头结构为研究对象,研究虎头结构复杂分布的32条焊缝焊接过程,针对不同焊接顺序方案下整体结构的焊接变形进行了定量数值模拟分析,为实际工程生产提供参考数据.
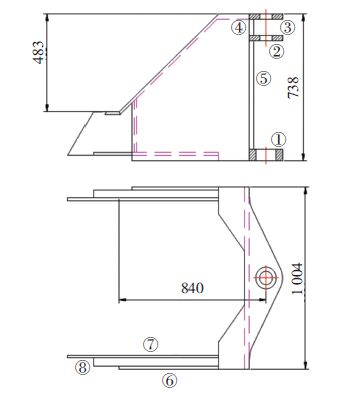
1 有限元模型建立 1.1 虎头结构有限元模型虎头的结构与尺寸如图 1所示.虎头由下连接板①、上/中连接板③与②、条板④、2块立板⑤、左右外侧板⑥、左右内侧板⑦、连接弯板⑧及连接底板⑨组成,主要外形尺寸为:1 004 mm,738 mm,483 mm,840 mm等.
|
图 1 虎头结构 |
建立虎头三维实体有限元模型,采用分块建模方式并划分网格,焊缝为角焊缝.由于模型尺寸大,为了减少计算量,提高计算效率并保证计算精度,网格划分整体上表现为由密到疏的过渡方式,即由于焊缝及其附近区域的温度和应力梯度变化大,因此对焊缝及其附近区域的网格加密处理,最小单元长为5 mm,对于尺寸超过1 m的模型,该尺寸能满足精度要求也能提高计算速度,在远离焊缝的区域网格划分较为稀疏.模型单元为八节点六面体类型,共含51 836个单元、84 100个节点,划分网格后的虎头有限元模型如图 2所示.

|
图 2 有限元网格模型 |
材料的热物理及力学参数均是温度的函数,随温度而变化,这对于焊接模拟结果的准确性有着重要的作用,文中模拟采用的材料为Q345,其各项性能参数随温度变化的情况见表 1.
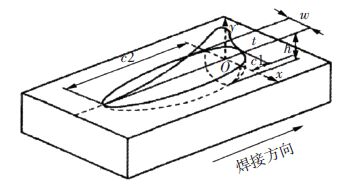
1.3 热源模型焊接热源模型是实现焊接过程数值模拟的基本条件.为了提高有限元计算的效率和精确性,选择恰当的热源是非常必要的.本实验采用的是CO2气体保护焊,因此为了让数值模拟更符合实际情况,文中采用最能接近电弧焊熔池精度的三维双椭球热源模型[20],如图 3所示.双椭球热源模型是一个体热源模型,前后两部分采用不同的表达式.
前半部分椭球热源表达式为
| $\eqalign{ & q\left( {x,y,z,t} \right) = {{6\sqrt 3 Q{f_f}} \over {wh{c_1}\pi \sqrt \pi }}\exp \left( { - 3{{{x^2}} \over {{w^2}}}} \right) \cr & \exp \left( { - 3{{{y^2}} \over {{h^2}}}} \right)\exp \left( { - 3{{{{\left( {z - v.t} \right)}^2}} \over {{c_1}^2}}} \right), \cr} $ | (1) |
后半部分椭球热源表达式为
| $\eqalign{ & q\left( {x,y,z,t} \right) = {{6\sqrt 3 Q{f_r}} \over {wh{c_2}\pi \sqrt \pi }}\exp \left( { - 3{{{x^2}} \over {{w^2}}}} \right), \cr & \exp \left( { - 3{{{y^2}} \over {{h^2}}}} \right)\exp \left( { - 3{{{{\left( {z - v.t} \right)}^2}} \over {{c_2}^2}}} \right). \cr} $ | (2) |
式中:Q为热源总功率,Q=ηIU,η为焊接热源热效率;v为焊接速度;ff和fr为前后椭球热源能量分数,且ff+fr=2;w为热源半宽;h为热源深度;c1为前半球长度;c2为后半球长度.
|
图 3 双椭球热源模型[12] |
计算时焊接规范按照生产参数为:电流I=350 A,电压U=30 V,焊接速度v=7 mm/s,热源效率η=0.7;热源参数:前半球长度c1=4 mm,后半球长度c2=7 mm,热源半宽w=4mm,热源深度h=5 mm,前椭球热源能量分数ff=1.4,后椭球热源能量分数fr=0.6.
另外位移边界条件的施加按照实际焊接生产的定位,虎头底部放在平台上,故Z方向位移约束;两臂的中心方向左右位移约束(Y向);连接板前后位移约束(X向),以便消除整体刚性位移.计算时,不同焊接顺序计算皆在同一边界条件下,因此焊接变形结果的对比性突出.
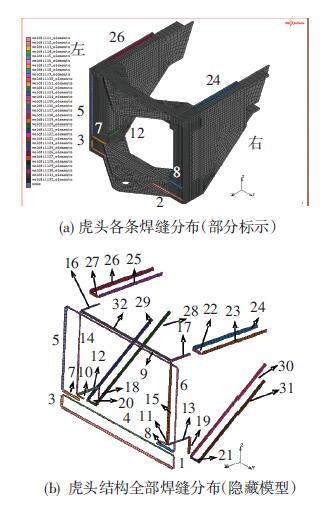
2 焊缝位置及焊接顺序方案 2.1 焊缝布置虎头结构复杂,由各个组成板焊接形成一体,共含32条主要焊缝,彩色单元为焊缝,其序号分配及具体位置如图 4所示.由于焊缝较多,不能完全显示,图中括号内表示被遮挡住的焊缝,可以从结构的对称性判断出被遮挡焊缝位置.从图 4可以看出,在虎头正面,‘焊缝2’与‘焊缝4’、‘焊缝5’与‘焊缝6’为对称焊缝;下连接板与立板的焊缝为‘焊缝9’;上连接板与左内侧板之间的‘焊缝16’,‘焊缝17’与之对称;上连接板与立板之间的‘焊缝32’,‘焊缝9’与之关于立板对称.表 2显示了对称焊缝之间的对应关系.
|
图 4 虎头焊缝位置及分布 |
| 表 2 对称焊缝序列 |
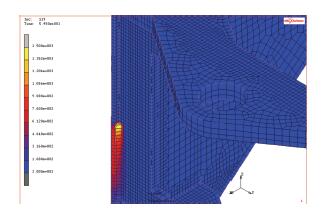
按照前面提到的焊接参数进行计算焊接温度场,图 5为焊接过程中电弧行进到‘焊缝5’时某一时刻(t=59.5 s)的瞬态温度场.显示的最高温度达1 500 ℃,表明材料熔化形成熔池,超过熔池温度的单元宽度为9 mm,深度为4.5 mm,与实际结构焊缝尺寸接近(焊缝宽度为10 mm,熔深为5 mm).建立的模型及参数符合实际焊接情况.
|
图 5 焊接温度场(t=59.5 s) |
根据虎头焊接结构的特点,焊缝多为T型角焊缝,故变形以角变形为主,以及由角变形沿焊缝长度方向分布不均匀而造成的扭曲.结合生产环节的可操作性,为了减少焊接变形,拟定焊接顺序的原则为:采取左右对称交替焊接顺序,原因是左右距离较远,焊接左边时产生的高温温度场对右边影响较小,这样会减小受热区,因而变形相应小.另外首先保证虎头大体框架的刚度,即框架的焊缝先焊.虎头正面/背面的焊缝首先依次焊接或左右交替焊接,然后进行左、右侧臂的焊接,加之整个结构具有对称性,所以可以多种组合的32条焊缝简化拟定出四种焊接顺序,焊接顺序方案见表 3.
| 表 3 焊接顺序方案 |
虎头结构焊接变形较为复杂,并不是表现出单一的某种变形,而是由不同部位(部件)的各自变形叠加而成,且皆由角变形引起.对于任何一种焊接顺序方案,在虎头几个不同部位,每种焊接顺序方案产生的焊接变形表现出大致类似的变形趋势,对比不同焊接顺序条件下各部位的最大变形点,可得到优化的焊接顺序.
图 6~图 8为虎头焊接变形趋势模拟图,该结构变形主要分析其四个部位的变形趋势,分别为:
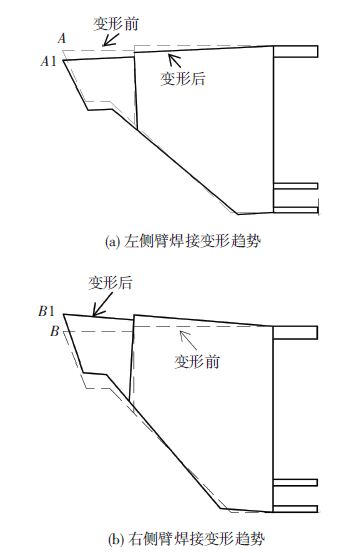
1) 变形1:左侧臂变形.如图 6(a)所示,可以看出,左侧臂整体绕O点下挠.可考察点A变化到点A1的Z向位移(ΔZA)来判断其焊接变形的大小.
| $\Delta {Z_A} = {Z_{{A_1}}} - {Z_A}.$ | (3) |
2) 变形2:右侧臂变形.如图 6(b)所示,可以看出,整个右侧臂结构焊接变形表现为绕O点上翘.可考察点B变化到点B1的Z向位移(ΔZB)来判断其焊接变形的大小.
| $\Delta {Z_B} = {Z_{{B_1}}} - {Z_B}.$ | (4) |
|
图 6 左/右侧臂焊接变形趋势 |
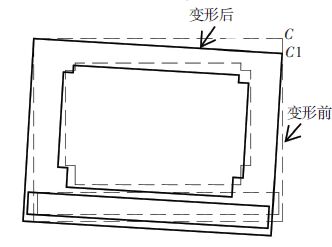
3) 变形3:正面框架扭转变形.如图 7所示,可以看出,框架发生了绕转,可以用最外角点C变化到点C1的Z向位移(ΔZC)、Y向位移(ΔYC)作为表征各顺序下的焊接变形量.
| $\Delta {Z_C} = {Z_{{C_1}}} - {Z_C}.$ | (5) |
| $\Delta {Y_C} = {Y_{{C_1}}} - {Y_C}.$ | (6) |
|
图 7 正面框架焊接变形趋势 |
4) 变形4:左右两侧臂收缩变形.如图 8所示为左右侧臂变形趋势,左、右侧臂上端角点D与E向内收缩偏移,下端角点F与G也向内收缩,表现出梯形状态.可以考察DE的位移ΔDE、FG的位移ΔFG.
| $\Delta DE = {D_1}{E_1} - DE.$ | (7) |
| $\Delta FG = {F_1}{G_1} - FG.$ | (8) |

|
图 8 左右两侧臂收缩变形趋势 |
综合对比四种焊接顺序条件下上述四类焊接变形的考察量,变形量最小的一组焊接顺序即为虎头的最优焊接顺序方案.
2.5 数值模拟结果图 9为虎头整体外观焊接变形模拟结果,可以看出,虎头表现出了所述的四类焊接变形.其中黑框线表示结构焊接前位置,焊后各部位产生了如上述分析所示的相应位移,彩色单元为变形后的结构.

|
图 9 虎头整体外观焊接变形 |
表 4为虎头的四种拟定的焊接顺序方案的焊接变形数据,变形量正负号表示焊接变形方向与模型坐标系正方向相同或相反,其绝对值为变形量大小.通过对比分析,可以看出,焊接变形综合效果上数值最小的是焊接顺序方案1,按照该焊接顺序,32道焊缝对称组焊,最终的焊接变形最小.其他的焊接方案左右侧臂变形均过大,对后续虎头结构的装配非常不利.
| 表 4 4种焊接方案的变形对比 |
对焊接顺序1的虎头结构进行了四种类型的焊接变形大小的实际测量,如图 10所示.产品图纸装配要求左右侧臂收缩变形ΔDE不超过15 mm,左/右侧臂上下变形ΔZA不超过10 mm,模拟结果数据均比图纸装配要求的要小,说明模拟结果符合虎头结构的验收要求.

|
图 10 虎头实物测量 |
焊接顺序方案1的模拟值与实测值直方图对比如图 11所示.

|
图 11 方案1模拟值与实测值比较 |
实际测量数据比模拟结果值要略小,但大体上相符.方案1中左侧臂实际变形ΔZA为7.8 mm,右侧臂变形ΔZB为9.4 mm,正面框架扭转变形ΔZC为8.3 mm,正面框架扭转变形ΔYC为3.9 mm,左右侧臂收缩变形ΔDE为13.4 mm,左右侧臂收缩变形ΔFG为11.8 mm.最大误差在8%之内,对于数值模拟是可接受范围.
3 结 论1) 建立了装载机后车架虎头的有限元模型,划分了网格,并进行了温度场数值模拟计算,计算结果验证了模型建立的准确性.
2) 虎头结构模拟结果表现出复杂的焊接变形,明确了焊接变形的分析思路,主要有左、右侧臂变形,正面框架扭转变形,左右两侧臂收缩变形.
3) 采用4种不同的焊接顺序进行焊接数值计算,结果表明,采用焊接顺序1时,各焊接变形量都最小,说明该方案为四种焊接顺序中最优方案.焊后实测结果表明,模拟结果误差在8%之内,证明模拟计算的正确性.
| [1] |
田锡唐. 焊接结构. 北京: 机械工业出版社, 1982 .
TIANXitang. Welded structure. Beijing: China Machine Press, 1982 .
( 0) 0)
|
| [2] |
方洪渊. 焊接结构学. 北京: 机械工业出版社, 2008 .
FANG Hongyuan. Welded structure. Beijing: China Machine Press, 2008 .
( 0) 0)
|
| [3] |
杨建国, 万清华, 戴志立, 等. 300MW锅炉汽包焊接变形的控制[J]. 焊接, 1996 (11) : 14 –16.
YANG Jianguo, WAN Qinghua, DAI Zhili, et al. Controlling for welding distortion of 300 MW steam drum[J]. Welding & Joining, 1996 (11) : 14 –16.
( 0) 0)
|
| [4] |
NOH S, KASADA R, KIMURA A, et al. Microstructure and mechanical properties of friction stir processed ODS ferritic steels[J]. Journal of Nuclear Materials, 2011, 417 : 245 –248.
DOI: 10.1016/j.jnucmat.2011.01.059 ( 0) 0)
|
| [5] |
薛忠明, 曲文卿, 柴鹏, 等. 焊接变形预测技术研究进展[J]. 焊接学报, 2003, 24 (3) : 87 –90.
XUE Zhongming, QU Wenqing, CHAI Peng, et al. Review on prediction of welding distortion[J]. Transactions of The China Welding Institution, 2003, 24 (3) : 87 –90.
( 0) 0)
|
| [6] |
张志英, 江志斌, 虞成全. 造船(中钢板)焊接变形的自动火焰矫正工艺系统[J]. 机械工程学报, 2006, 42 (1) : 196 –201.
DOI: 10.3901/JME.2006.01.196 ZHANG Zhiying, JIANG Zhibin, YU Chengquan. Automated method of flame rectification process of welding distortion for mediate steel plate and system in shipbuilding[J]. Chinese Journal of Mechanical Engineering, 2006, 42 (1) : 196 –201.
DOI: 10.3901/JME.2006.01.196 ( 0) 0)
|
| [7] |
SATTARI-FAR I, JAVADI Y. Influence of welding sequence on welding distortions in pipes[J]. International Journal of Pressure Vessels and Piping, 2008, 85 : 265 –274.
DOI: 10.1016/j.ijpvp.2007.07.003 ( 0) 0)
|
| [8] |
徐济进, 陈立功, 汪建华, 等. 基于固有应变法筒体对接多道焊焊接变形的预测[J]. 焊接学报, 2007, 28 (1) : 77 –80.
XU Jijin, CHEN Ligong, WANG Jianhua, et al. Prediction of distortion based on inherent strain method in multipass girth-butt welded pipes[J]. Transactions of The China Welding Institution, 2007, 28 (1) : 77 –80.
( 0) 0)
|
| [9] |
周广涛, 刘雪松, 闫德俊, 等. 顶板焊接顺序优化减小焊接变形的预测[J]. 焊接学报, 2009, 30 (9) : 109 –112.
ZHOU Guangtao, LIU Xuesong, YAN Dejun, et al. Prediction for welding deformation reducing by welding sequence optimization of upper plate[J]. Transactions of the China Welding Institution, 2009, 30 (9) : 109 –112.
( 0) 0)
|
| [10] |
李军, 张文锋. 机械挤压矫正焊接变形的模拟与试验研究[J]. 材料科学与工艺, 2013, 21 (1) : 134 –137.
LI Jun, ZHANG Wenfeng. Rectifying buckling distortion by extruding thin-plate weldments in parallel direction to weld[J]. Materials Science and Technology, 2013, 21 (1) : 134 –137.
( 0) 0)
|
| [11] |
张学秋, 杨建国, 刘雪松, 等. 焊接顺序对整体叶盘圆度影响的有限元分析[J]. 焊接学报, 2010, 31 (3) : 57 –60.
ZHANG Xueqiu, YANG Jianguo, LIU Xuesong, et al. Finite element anlysis of welding sequence impact on blisk roundness[J]. Transactions of The China Welding Institution, 2010, 31 (3) : 57 –60.
( 0) 0)
|
| [12] |
黄海瀚, 周广涛. 装载机后车架焊接顺序优化的数值仿真[J]. 计算机辅助工程, 2014, 23 (3) : 30 –34.
HUANG Hanhan, ZHOU Guangtao. Numerical simulation on welding sequence optimization of loader rear frame[J]. Computer Aided Engineering, 2014, 23 (3) : 30 –34.
( 0) 0)
|
| [13] |
王苹, 王强, 刘雪松, 等. 基于FEM的高速列车地板结构焊接顺序优化[J]. 焊接学报, 2012, 33 (8) : 45 –48.
WANG Ping, WANG Qiang, LIU Xuesong, et al. Welding sequence optimization for high-speed rail floor based on FEM[J]. Transactions of The China Welding Institution, 2012, 33 (8) : 45 –48.
( 0) 0)
|
| [14] |
SOUTO GRELA J, BLANCO VIANA E B, MARTINEZ D, et al. Numerical simulation in welding process:optimizing structures with sequence and inertial study[J]. Matériaux & Techniques, 2012, 100 (4) : 317 –326.
( 0) 0)
|
| [15] |
任鹏, 张伟, 郭子涛, 等. Numerical simulation for deformation of multi-layer steel plates under underwater impulsive loading[J]. 哈尔滨工业大学学报(英文版), 2012, 19 (3) : 68 –72.
REN Peng, ZHANG Wei, GUO Zitao, et al. Numerical simulation for deformation of multi-layer steel plates under underwater impulsive loading[J]. Journal of Harbin Institute of Technology, 2012, 19 (3) : 68 –72.
( 0) 0)
|
| [16] |
李江飞, 齐海波, 任德亮, 等. 薄壁多焊缝复杂构件焊接过程的数值模拟[J]. 焊接学报, 2015, 36 (1) : 87 –90.
LI Jiangfei, QI Haibo, REN Deliang, et al. Numerical simulation of welding process on thin-walled multi-welds complex component[J]. Transactions of The China Welding Institution, 2015, 36 (1) : 87 –90.
( 0) 0)
|
| [17] |
张伟玮, 韩聪, 苑世剑. 高强钢22MnB5扭力梁热成形热力耦合数值模拟[J]. 材料科学与工艺, 2014, 22 (3) : 16 –22.
ZHANG Weiwei, HAN Cong, YUAN Shijian. Hot forming processing simulation of torsion beam of high strength steel 22MnB5[J]. Materials Science and Technology, 2014, 22 (3) : 16 –22.
( 0) 0)
|
| [18] |
ISLAM M, BUIJK A, RAIS-ROHANI M, et al. Simulation-based numerical optimization of arc welding process for reduced distortion in welded structures[J]. Finite Elements in Analysis and Design, 2014, 84 : 54 –56.
DOI: 10.1016/j.finel.2014.02.003 ( 0) 0)
|
| [19] |
崔晓芳, 林健, 兆文忠. 高速动力车构架侧梁焊接结构优化研究[J]. 材料科学与工艺, 2004, 12 (6) : 606 –609.
CUI Xiaofang, LIN Jian, ZAO Wenzhong. Optimization of welded structure in bogie frame of high-speed locomotive[J]. Materials Science and Technology, 2004, 12 (6) : 606 –609.
( 0) 0)
|
| [20] |
GOLDAK J, CHAKRARTI A, BIBBY M. A new finite element model for welding heat sources[J]. Metallurgical Materials Transactions B, 1984, 15 (2) : 299 –305.
DOI: 10.1007/BF02667333 ( 0) 0)
|
| [21] |
吴华英, 郭成, 王永信, 等. 轿车后围板成形过程数值模拟及参数优化[J]. 材料科学与工艺, 2013, 21 (2) : 83 –89.
WU Huaying, GUO Cheng, WANG Yongxin, et al. Numerical simulation and parameter optimization in forming process of an automobile squab panel[J]. Materials Science and Technology, 2013, 21 (2) : 83 –89.
( 0) 0)
|
| [22] |
GANNON L, LIU Y, PEGG N, et al. Effect of welding sequence on residual stress and distortion in flat-bar stiffened plates[J]. Marine Structures, 2010, 23 : 385 –404.
DOI: 10.1016/j.marstruc.2010.05.002 ( 0) 0)
|
| [23] |
王兴路, 贺利乐. 焊接顺序对机械结构疲劳寿命影响研究[J]. 热加工工艺, 2013, 42 (11) : 180 –182.
WANG Xinglu, HE Lile. Study on effect of welding sequence on fatigue life of mechanical structure[J]. Hot Working Technology, 2013, 42 (11) : 180 –182.
( 0) 0)
|
| [24] |
李晓东, 李春广, 朱志民, 等. 铝合金薄板MIG焊焊接变形仿真预测的工程应用[J]. 焊接学报, 2014, 35 (2) : 104 –108.
LI Xiaodong, LI Chunguang, ZHU Zhimin, et al. Engineering applications of MIG welding deformation simulation of aluminum alloy sheet[J]. Transactions of the China Welding Institution, 2014, 35 (2) : 104 –108.
( 0) 0)
|
| [25] |
DONG Wenchao, LU Shanping, LU Hao, et al. Numerical simulation and control of welding distortion for double floor structure of high speed train[J]. Acta Mechanica Sinica, 2014, 30 (6) : 849 –859.
DOI: 10.1007/s10409-014-0108-8 ( 0) 0)
|
 2016, Vol. 24
2016, Vol. 24


