上海应用技术大学 材料科学与工程学院,上海 201418
School of Materials Science and Engineering,Shanghai Institute of Technology,Shanghai 201418,China
近年来,随着国际经济的高速发展,对金属的需求量越来越大.人们对金属总量需求增加的同时,对一些高性能金属的需求量也随之增加.尤其是一些合金资源消耗少、综合性能高的金属材料更是受到了业界的强烈追求.因此,对金属材料组织演变与晶粒细化对其性能的研究一直是材料科学工作者关注热点,其中强烈塑性变形(severe plastic deformation,即SPD)对金属组织性能的研究就是一例.例如,郑丽静等人通过等径角挤压(ECAP)工艺,将纯铝的平均晶粒尺寸细化到600 nm以下,强度达到163.1 MPa,增加到原来的2.5倍[1-2].上官丰收等人利用高压扭转(HPT)法,对纯铜进行研究,将纯铜从原始晶粒尺寸13.24 μm细化到0.27 μm[3].其他工艺例如累积轧制(ARB)[4-5],多向锻造(MF)[6-7]对强烈塑性变形与金属组织演变关系进行了深入的研究,结果显示多弯曲后,热轧带材的表面晶粒取得了很大的进展.最近也有人用热轧后多弯曲的方法然对铁素体进行研究,变形后铁素体最小晶
粒尺寸达到1.4 μm[8],国内外对利用塑性弯曲变形工艺改善金属材料组织性能的研究却比较少.本文提出的塑性弯曲变形对金属组织性能影响的研究,不仅拓宽了传统塑性加工技术的应用领域,使传统金属材料的性能得以较大幅度的提高,而且还为提升金属材料的使用效率提供了更广阔的空间.同时利用塑性弯曲变形改善金属材料的组织与性能也在一定程度上减缓上述SPD工艺的复杂性和难以大批量生产的不足,以进一步降低生产加工成本和实现工业化生产.本文以H85黄铜板材为对象,采用MARC有限元分析软件等计算不同弯曲半径与板厚之比(r/h)对金属材料内部累积应变的影响,同时结合金相组织分析和显微硬度测定,进一步确定其内部晶粒尺寸的变化规律和对性能的影响等.
1 试 验 1.1 试验方案设计为了分析金属板材反复塑性弯曲变形、不同径厚比r/h等对板材内部累积应变的影响,以进一步确定金属板材的组织与性能的变化规律.特设计了如图 1所示的金属板材反复塑性弯曲变形试验方案.试样在特定的模具中,进行“弯曲—压平—反向弯曲—再压平”为一个工作周期(简称:1T),由此重复这一反复塑性弯曲过程,即:2T、3T、4T……,由此评价金属板材在其反复塑性弯曲过程中的应变累积效应.

|
图 1 金属板材反复塑性弯曲变形试验方案 |
根据图 1所示的试验方案,设计制作了不同弯曲曲率半径的组合模具,如图 2所示.在此模具上实现不同径厚比(r/h)的反复塑性弯曲变形试验.加载弯曲试验在30吨压力试验机上进行.

|
图 2 金属板材反复弯曲变形试验的模具和弯曲试验 |
试验的材料是:H85黄铜,其化学成分为(质量分数,%):Cu84-86,Fe≤0.5,Pb≤0.03,Ni≤0.3,杂质总和≤0.1,余量为Zn.试样尺寸为:100 mm×25 mm×4 mm的板材,试样为完全退化状态.
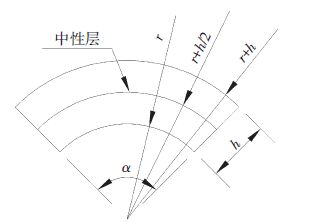
1.3 金属板材反复塑性弯曲变形累积应变量计算根据金属板材塑性弯曲变形过程中的几何尺寸变化,计算其累积应变量.如图 3所示,假定金属板材塑性弯曲变形过程中,沿厚度方向的中性面几何长度不变,而其内外侧发生塑性压缩或延伸变形.依据塑性变形叠加效应,确定其内部的塑性累积变形量.
|
图 3 金属板材弯曲变形示意图 |
根据设计的试验方案,试样工件的一个周期弯曲变形,即经过“平直—弯曲—压平—反向弯曲—再压平”,其累积真应变量为:
设试样工件原长(即中性面长度):l0=α(r+h/2)
试样工件上表面受延伸变形后长度为: l1=α(r+h)
试样工件下表面受压缩变形后长度为:l2=αr
其中:r为金属板材试样的弯曲曲率半径、h为金属板材试样的厚度.
以上表面为例,工件由平直到弯曲的真应变为
| $${e_1} = \ln {{{l_1}} \over {{l_0}}},$$ | (1) |
又由弯曲到平直的真应变为
| $${e_2} = \ln {{{l_0}} \over {{l_1}}},$$ | (2) |
反向弯曲变形的真应变为
| $${e_3} = \ln {{{l_2}} \over {{l_0}}},$$ | (3) |
再次由弯曲展平的真应变为
| $${e_4} = \ln {{{l_0}} \over {{l_2}}},$$ | (4) |
由(1) ~(4) 可得到一个弯曲变形周期的工件上表面累积真应变为
| $$e = \sum\limits_{i = 1}^4 {\left| {{e_i}} \right|} = 2\ln \left( {1 + {{{1 \over r}} \over h}} \right)$$ | (5) |
因此,n个周期弯曲变形后,工件上表面的累积真应变为
| $$\varepsilon \Sigma = 2n\ln \left( {1 + {{{1 \over r}} \over h}} \right) \cdot \left( {n = 1,2,3, \cdots } \right)$$ | (6) |
同样推导,距离中性面x距离的累积真应变为
| $$\varepsilon \Sigma = 2n\ln \left( {{{r/h + 1/2 + x/h} \over {r/h + 1/2 - x/h}}} \right) \cdot \left( {n = 1,2,3, \cdots } \right)$$ | (7) |
式中:x=0~h/2,即x=0试样中性面处,x=h/2为试样上下表面.
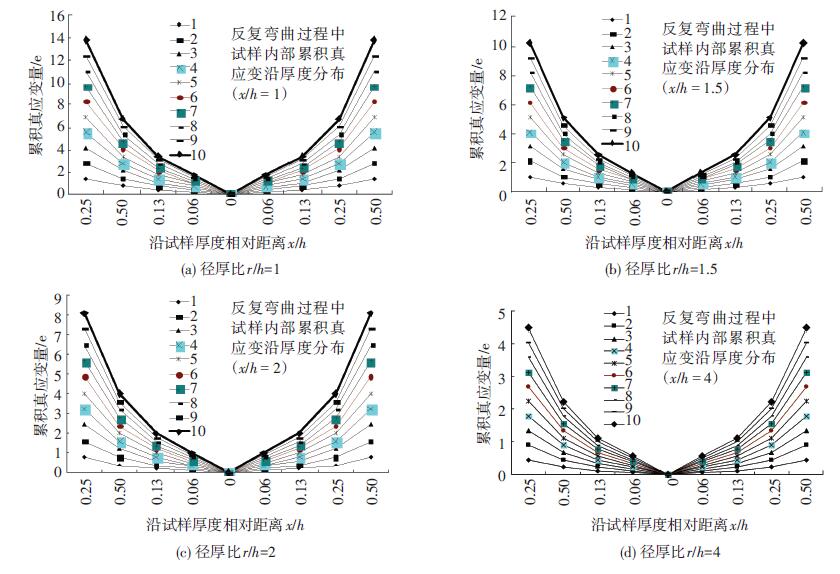
根据上述推导的金属板材在塑性弯曲变形过程中,其内部的累积真应变计算,如图 4所示.
|
图 4 不同径厚比r/h试样反复弯曲1~10个周期的累积真应变分布 |
由图 4所示的累积真应变量计算可以看出,金属板材反复弯曲过程中,其内部累积真应变量随着弯曲周期(n)的增加而线性增大、随着径厚比(r/h)的减小而增大、随着距中性面距离(x/h)的增加而增大.
2 金属板材弯曲变形有限元模拟计算金属板材弯曲变形是一个非线性的塑性变形过程.本文采用MARC有限元分析软件对金属板材弯曲变形过程进行模拟计算.MARC软件具有的强大接触计算能力,丰富的用户子程序接口以及非线性问题求解技术,使在处理金属板材塑性弯曲变形这类问题时具有独到的优势[8].
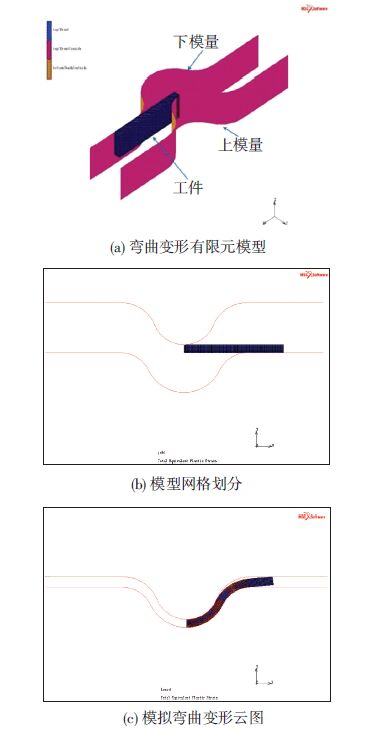
根据本文设计的金属板材弯曲试验进行有限元计算建模时,假定其为理想弯曲变形,由于其变形的对称性,为了节省模拟计算时间,金属板材采用二分之一建模,所建的金属板材弯曲有限元模型如图 5(a)所示.
|
图 5 金属板材的有限元模型和网格划分及变形云图 |
弯曲变形所采用的模具为硬质合金材料,其强度远大于H85黄铜,故在有限元计算中可以不考虑其变形,视为刚形体.金属板材塑性弯曲变形过程中的内部应变分布模拟计算如图 5(b)所示.
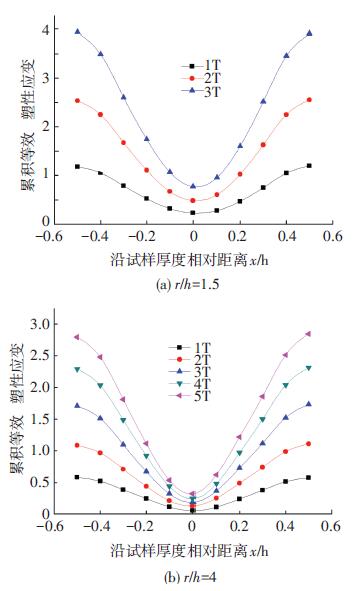
3 有限元模拟计算结果与分析 3.1 有限元模拟应变分析在金属板材的反复弯曲变形过程中,板材厚度上的塑性应变分布和变化规律对金属材料的组织与性能有着非常重要的影响.本文给出了在两个不同弯曲曲率半径与板厚之比(径厚比:r/h=1.5和4) ,在经过不同周期(1T~5T)的弯曲变形后,金属板材沿厚度对称面上下的等效塑性应变分布,如图 6所示.
|
图 6 金属板材在不同模具中弯曲变形后总的等效塑性应变 |
由图 6可知,金属板材在反复弯曲时,靠近上下两表面部位应变累积量最大,而工件中心面处,应变量最小,但却不为零.这是由于板材弯曲变形时,以应变中性层为界,外层纤维受延伸变形而导致厚度减薄,内层纤维受压缩变形而导致厚度增加.对于板料大曲率塑性弯曲过程中,其中性层向内移动,其结果使板料中心面与应力中性层不重合,中心面处发生了少量的塑性变形[10-12].由图 6也可知在相同的弯曲周期下,随着径厚比的减小,等效塑性应变累积量增加,这是因为当经厚比减小时,工件相对弯曲变形的程度增大,板材塑性变形量增大,因而应变量增大.
从有限元分析的结果还发现,金属板材经过多周期弯曲变形后,其内部的累积应变量是成倍增加,其分布规律这与式(6) 和式(7) 的计算结果基本一致,其数值上的误差是由于式(6) 和式(7) 的计算式推导中,假定金属板材的中性面几何长度不变引起.
3.2 金属板材弯曲变形后金相组织实验分析为了进一步分析H85黄铜板材经过反复塑性弯曲变形后,其内部累积应变对金属组织影响的效应.沿试样厚度方向不同位置取样(如图 7所示,为取样位置),进行金相组织观察分析.
|
图 7 沿试样厚度方向取样的位置 |
所取的金相试样为:弯曲变形前的完全退火处理试样、径厚比r/h= 1.5的弯曲变形3个周期试样、径厚比r/h=4的弯曲变形5个周期试样,试样的金相显微组织如图 8所示.从图 8(a)可以看出,退火料的晶粒多为等轴状,平均晶粒尺寸约为60 μm.图 8(b)和图 8(d)分别为r/h=1.5,3个周期弯曲变形和r/h=4,5个周期弯曲变形后中性面处金相组织,晶粒发生一定的细化破碎和细化,平均晶粒尺寸约为50 μm.这也反映了前所分析的弯曲过程中试样中性面部位有少量塑性变形的结论.图 8(c)为r/h=1.5,3个周期弯曲变形的边部取样金相图,晶粒细化破碎较大,部分晶粒尺寸小于10 μm.图 8(f)为r/h=4,3个周期弯曲变形的边部取样金相图,晶粒细化破碎比较大,部分晶粒尺寸小于15 μm.即金属的晶粒破碎程度随着径厚比(r/h)的减小而增加.图 8(e)、(f)和(g)分别为r/h=4,经过1个周期,3个周期和5个周期弯曲变形的边部组织金相图,平均晶粒尺寸分别约为50,30和20 μm.即金属的晶粒破碎程度随着变形周期的增加而增加.

|
图 8 H85黄铜退火后板材和经过不同周期弯曲变形后试样的金相组织. |
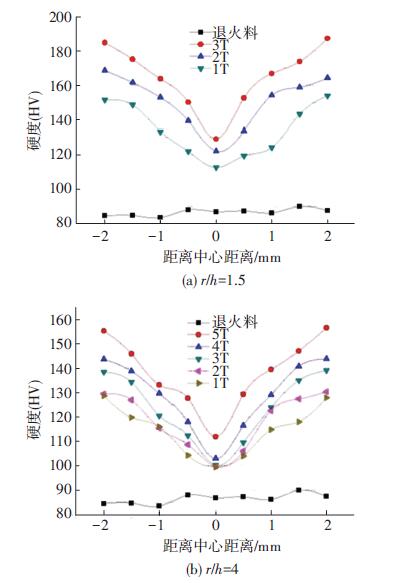
在试样径厚比r/h= 1.5和4,并经过不同周期弯曲变形后,金属板材试样的内部晶粒尺寸发生变化,同时用MH-5显微硬度计测定其显微硬度沿金属板材厚度,从中心部位到边部也相应发生了变化.如图 9所示,为金属板材内部显微硬度沿厚度的变化情况.
|
图 9 金属板材变形前后不同位置的显微硬度值 |
H85黄铜板材退火后的平均硬度为86.3 HV,经过径厚比r/h=1.5,进行1T,2T,3T弯曲变形后,金属板材边部硬度最大值分别为153.9 HV,168.6 HV,187.3 HV ,分别增加了117.0%,95.4%,78.3%.经过径厚比r/h=4,弯曲变形之后,金属板材边部处硬度也都有很大的提高,经过五个周期弯曲变形后,最大硬度增加81.5%,如表 1所示.
| 表 1 金属板材变形前后边部显微硬度值 |
H85黄铜板料显微硬度的变化,反映了工件在变形之后其内部应变的累积效应.在距离中性面较远的边部处(x/h比较大的部位),由于其累积应变比较大,导致其位错密度增加,位错的交互作用也随之增加,使其显微硬度提高.对比图 9(a)和图 9(b)可以发现,金属板材在相同的弯曲周期下,随着径厚比的增小,显微硬度均呈现增大趋势,这主要是因为在相同的弯曲周期下,随着径厚比的减小,板材的累积应变量增加,位错密度也随之增加,位错运动时的相互交割加剧,产生固定割阶等障碍,使位错运动阻力增大,引起变形抗力的增加,由此提高了金属板材的强度和硬度[13].
由上图我们还可以发现,在反复塑性弯曲变形过程中,板料中性面部位显微硬度也得到提高,并随着径厚比(r/h)的减小而增大.这是由于由于中性层的位移[14-15]使中间部位也存在一定量的塑性变形所致.
4 结 论1) 金属板材经过反复塑性弯曲变形后,可有效提高其内部的累计应变量.累积应变量随着弯曲周期(n)的增加而线性增大、随着径厚比(r/h)的减小而增大、随着距中性面距离(x/h)的增加而增大.
2) 金属板材的反复塑性弯曲变形有限元计算表明,其内部的等效累积应变不仅在板料表层存在,而且可以渗透到金属板料的中心部位.
3) 金属板材的反复塑性弯曲变形可以有效地破碎和细化晶粒,其破碎细化效果随径厚比r/h的减小而增加,并由板材的中性面到其边缘而增强.
4) 金属板材的反复塑性弯曲变形可以有效强化其强度性能指标,板材表面的显微硬度提高了一倍以上,而且其中心层的显微硬度也提高了20%以上.
| [1] |
郑立静, 陈昌麒, 周铁涛, 等. ECAP细晶机制及对纯铝显微组织和力学性能的影响[J]. 稀有金属材料与工程, 2001, 12 (12) : 1325 –1328.
ZHENG Lijing, CHEN Changqi, ZHOU Tietao, et al. Grain-refining mechanism of ECAP and its effect on microstructures and mechanical properties of pure AL[J]. Rare Metal Materials and Engineering, 2001, 12 (12) : 1325 –1328.
( 0) 0)
|
| [2] |
肖代红, 陈康华. 等径角挤压对Al-Cu-Mg-Ag 合金组织性能的影响[J]. 材料科学与工艺, 2011, 19 (6) : 129 –132.
XIAO Daihong, CHEN Kanghua. Effect of equal channel angular pressing on microstructure and properties of Al-Cu-Mg-Ag aluminum alloys[J]. Materials Science and Technology,, 2011, 19 (6) : 129 –132.
( 0) 0)
|
| [3] |
上官丰收, 钱桂安, 洪友士. 限定型高压扭转变形分析[J]. 塑性工程学报, 2009, 160 (1) : 134 –137.
SHANGGUAN Fengshou, QIAN Guian, HONG Youshi. Deformation analysis of copper samples subjected to destined high pressure torsion[J]. Journal of Plasticity Engineering, 2009, 160 (1) : 134 –137.
( 0) 0)
|
| [4] |
TSUJI N, SAITO Y, UTSUNOMIYA H, et al. Ultra-fine grained bulk steel produced by accumulative roll-bonding (ARB) process[J]. Scripta Materialia, 1999, 40 (7) : 795 –800.
DOI: 10.1016/S1359-6462(99)00015-9 ( 0) 0)
|
| [5] |
SAITO Y, TSUJI N, UTSUNOMIYA H, et al. Ultra-fine grained bulk aluminum produced by accumulative roll-bonding (ARB) process[J]. Scripta Materialia, 1998, 39 (9) : 1221 –1227.
DOI: 10.1016/S1359-6462(98)00302-9 ( 0) 0)
|
| [6] |
张小明, 张廷杰, 田锋, 等. 多向锻造对改善7075铝合金性能的作用[J]. 稀有金属材料与工程, 2003, 32 (05) : 372 –374.
ZHANG Xiaoming, ZHANG Tingjie, TIAN Feng, et al. Effects of multi-direction forging on improving properties of 7075 aluminum alloy[J]. Rare Metal Materials and Engineering, 2003, 32 (05) : 372 –374.
( 0) 0)
|
| [7] |
GUO Q, YAN H G, CHEN Z H, et al. Grain refinement in as-cast AZ80 Mg alloy under large strain deformation[J]. Materials Characterization, 2006, 58 (2) : 162 –167.
( 0) 0)
|
| [8] |
NAKATA N, MATSUBARA Y, HIRUTA T. Thermal analysis of strip in multi-bending process after hot rolling[J]. ISIJ International, 2013, 53 (5) : 874 –879.
DOI: 10.2355/isijinternational.53.874 ( 0) 0)
|
| [9] |
冯超, 孙丹丹, 陈火红. 全新Marc实例教程与常见问题解析. 中国水利水电出版社, 2011 .
Feng Chao, Sun Dandan, Chen Huohong. The new Marc example tutorial and common problems. China Water Conservancy and Hydropower Press, 2011 .
( 0) 0)
|
| [10] |
MATSUBARA Y, NAKATA N, HIRUTA T. Effect of accumulative bending conditions on grain refinement on hot-rolled sheet[J]. ISIJ International, 2013, 53 (2) : 274 –278.
DOI: 10.2355/isijinternational.53.274 ( 0) 0)
|
| [11] |
官英平, 赵军. 板料弹塑性弯曲应力应变中性层位置关系探讨[J]. 塑性工程学报, 2002, 9 (02) : 39 –41.
Guan Yingping, Zhao Jun. Research on place of stress and strain neutral layer in elastic bending of plate[J]. Journal of Plasticity Engineering, 2002, 9 (02) : 39 –41.
( 0) 0)
|
| [12] |
官英平, 张庆, 赵军. 中性层内移对弯曲回弹的影响[J]. 锻压技术, 2007, 02 (02) : 26 –28.
Guan Yingping, Zhang Qing, Zhao Jun. Influence of neutral layer inside displacement on bending springback[J]. Forging & Stamping Technology, 2007, 02 (02) : 26 –28.
( 0) 0)
|
| [13] |
崔忠圻, 谭耀春. 金属学与热处理. 机械工业出版社, 2012 .
CUI Zhongqi, TAN Yaowen. Metal science and heat treatment. Machinery Industry Press, 2012 .
( 0) 0)
|
| [14] |
贾美慧, 唐承统, 刘检华. 管材弯曲中应力中性层位移计算与影响因素分[J]. 材料科学与工艺, 2014, 22 (2) : 112 –116.
JIA Meihui, TANG Chengtong, LIU Jianhua. The calculation and influencing factors analysis of stress neutral layer displacement in tube bending[J]. Materials Science and Technology, 2014, 22 (2) : 112 –116.
( 0) 0)
|
| [15] |
Arya Mirsepasi, Mahmoud Nili-Ahmadabadi, Mohammad Habibi-Parsa, et al. Microstructure and mechanical behavior of martensitic steel severely deformed by the novel technique of repetitive corrugation and straightening by rolling[J]. Materials Science and Engineering A, 2012, 551 : 32 –39.
DOI: 10.1016/j.msea.2012.04.073 ( 0) 0)
|
 2016, Vol. 24
2016, Vol. 24


