2. 湖南信息职业技术学院,长沙 410004
2. Hunan College of Information, Changsha 410200, China
45CrNiMoVA是一种低合金高强度钢,主要用于制作飞机发动机曲轴、大梁、起落架等高强度结构零部件及扭力轴、变速器箱轴、摩擦离合器轴等重载荷的轴类零件[1].但是,45CrNiMoVA因强度和硬度高,导致其切削加工困难.
材料本构关系模型对制定科学的切削加工工艺具有重要的指导意义.同时,材料的本构关系模型是切削加工有限元模拟的基础[2],直接决定着有限元模拟结果的精确性.目前,常见的本构模型参数拟合大多是在低温、低应变条件下完成的,无法适应高速切削仿真的要求[3].因此,建立材料的流变本构模型具有重要的学术和工程意义[4].
国内在近几年来对切削过程的仿真研究也取得了不少的成果.解丽静等使用“差分”磨损模型就刀具磨损进行了预测[5];黄志刚、柯映林等基于切削加工的热弹塑性方程并在一定的假设条件下,建立了金属切削的热力耦合有限元模型[6];王洪祥等建立了KDP晶体超精密切削加工中应力应变的预测模型[7];常艳艳、孙涛等基于显示动力学和热力耦合建立了硬铝合金微米级超精密车削的有限元模型[8];严宏志、龚黎军通过准静态压缩试验及正交切削试验建立了20CrMo材料的热-黏塑性本构模型,在此基础上对切削过程中的切削力和切削温度进行了仿真[9].
本文就高强度钢45CrNiMoVA的流变本构方程进行研究分析,通过准静态扭转试验和直角自由切削试验建立了材料的Johnson-Cook 材料本构模型,并通过有限元仿真和切削试验验证了模型的准确性.最后,利用VB和C语言,开发了包括拉伸压缩试验、扭转试验、霍普金森压杆试验和直角自由切削等试验为基础的Johnson-Cook材料本构集成建模系统.
1 Johnson-Cook本构模型材料的本构模型是材料流动应力与应变、应变率及温度等变形参数之间的函数关系.Johnson-Cook本构模型具有形式简单、应用范围广等优点,是高应变率、高温条件下理想的刚塑性强化模型,适于描述材料在大应变率下的应力-应变关系,其表达式[10]为
| $\begin{align} & \sigma =\left( A+B{{\varepsilon }^{n}} \right)\left[ 1+C\left( \ln \left( 1+\frac{{\dot{\varepsilon }}}{{{{\dot{\varepsilon }}}_{0}}} \right) \right) \right]\centerdot \\ & \left[ 1-{{\left( \frac{T-{{T}_{r}}}{{{T}_{m}}-{{T}_{r}}} \right)}^{m}} \right]. \\ \end{align}$ | (1) |
式中:σ为流动应力;A、B、C、n、m
为确定式(1) 中材料的本构参数,分别进行了准静态扭转试验、低速直角自由切削试验及高速直角自由切削试验.利用准静态扭转试验确定材料的屈服强度(A)、应变强化常数(B)及应变硬化指数(n);利用低速直角自由切削试验确定参数C的回归方程;利用高速直角自由切削试验确定热软化系数(m).最后,针对试验结果中参数C出现负值这一情况,对参数C的影响因素进行了分析.
2.2 试验方案选择45CrNiMoVA属于高强度钢,其主要力学性能如表 1所示.在这里,采用更为常见的准静态试验来拟合本构方程的参数A、B和n.
| 表 1 45CrNiMoVA的主要力学性能 Table 1 The main mechanical properties of 45CrNiMoVA |
通过准静态试验,不仅要拟合得到参数A、B和n,同时还需要与直角自由切削试验数据结合,推导高应变率下的参数C,而直角自由切削的应变比较大,为减小数值外推带来的误差,需选择能得到大应变的试验,而45CrNiMoVA属于高强度钢,传统的拉伸、压缩试验较难得到大应变,因此采用扭转试验与切削试验相结合的方法计算材料的本构模型[11].
为使得切削试验中的应变率与扭转试验的应变率接近,先进行低速下的直角自由切削试验.为确定Johnson-Cook模型中的参数,通过准静态扭转试验和直角自由切削试验相结合,采用分析模型计算取代快速落刀试验来确定剪切角,适用范围更广,避免了试验制约[12].通过直角自由切削试验中得到的Johnson-Cook模型参数,更接近切削过程中材料在高应变及高应变率条件下的真实变形.
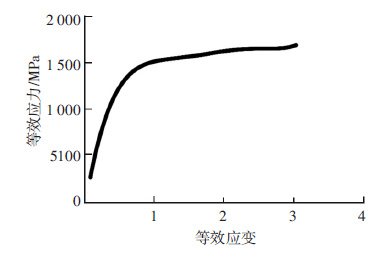
2.3 准静态扭转试验根据《GB/T 10128—2007金属材料室温扭转试验方法》,分别以6和18 (°)/min的速度对45CrNiMoVA试样进行连续扭转试验,试验设备为TNS-DW微机控制扭转试验机.取0.03为参考应变率,基于该应变率选择其他应变率参数.通过试验所得的扭矩-转角结果可计算得到真实剪应变和真实剪应力,经过处理后的剪应力-剪应变曲线如图 1所示.
由于扭转试验在室温下进行,且应变率较低,因此可以忽略温度和应变率对材料流变应力的影响.Johnson-Cook公式可以简化为
| $\sigma =\left( A+B{{\varepsilon }^{n}} \right).$ | (2) |
对比理想的塑性体应力-应变关系,材料在扭转过程中屈服点附近无明显平台现象,参考工程中条件屈服极限的计算方法,取A=σ0.2,得到材料的屈服极限σs=1 240 MPa,即式(2) 中的A值.使用最小二乘法计算B和n的值,即:
| $\ln \left( \sigma -A \right)=\ln B+n\ln \bar{\varepsilon }.$ | (3) |
令
|
图 1 等效应力-应变曲线 Figure 1 The equivalent stress-strain curve |
通过直角自由切削试验研究应变率对材料流变塑性的影响.将试验材料45CrNiMoVA加工成外径30 mm、厚度2.3 mm的薄壁管料.刀具选用TiN涂层刀具,前角为8°,后角为7°.在切削达到稳态条件后,使用Kistler测力仪记录三向切削力.收集不同切削条件下的切屑,在每一切屑上选择不同位置的5个点测量其厚度值,求其平均切屑厚度tc.为拟合J-C方程中的应变率强化系数C和热软化系数m,分别设计了低速直角自由切削试验和高速直角自由切削试验.试验切削参数及测得结果如表 2所示.
| 表 2 切削试验参数及测定结果 Table 2 Cutting test parameters and measurement results |
由表 2中的前22组试验数据拟合参数C的值.结合相同应变条件下的扭转数据与切削数据,根据Oxley切削理论[13]及本构模型的推导方法[14],不同切削条件下参数C的计算结果如表 3所示.经过二元线性回归,得到参数C的回归方程为
| $C=0.006-0.0001v-2.879f.$ | (4) |
| 表 3 低速切削试验参数及计算结果 Table 3 Cutting test parameters and calculation results at low velocity |
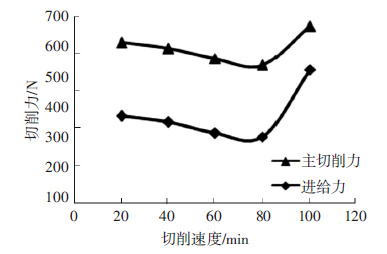
为拟合热软化系数m,进行了高速直角自由切削试验(表 2,试验23-27) .试验条件:保持进给量不变,增大切削速度.切削力随切削速度的变化结果如图 2所示.对比切削力和切屑厚度发现,当速度为100 m/min时,切削力和切屑厚度的规律与前面明显不同,切屑形态发现已呈锯齿型,而锯齿形并不符合Oxley切削理论,因此取速度从10~80 m/min的数据来拟合参数m.由于很难使用试验方法测量剪切区的温度,因此利用Oxley切削理论和Boothroyd温度模型计算各组数据的温升[15].通过计算,得到高速条件下参数m的拟合结果见表 4,将其中数据取平均值得m=1.26.至此完成Johnson-Cook本构模型中全部参数的确定.
|
图 2 切削力随切削速度的变化曲线 Figure 2 Cutting force changing with cutting speed of curve |
| 表 4 高速切削试验参数及计算结果 Table 4 Cutting test parameters and calculation results at high velocity |
由表 3可知,第15和16组的数据中参数C出现了负值的情况,该现象在其他类似试验中同样经常出现,在此就参数C的影响因素进行分析.
由于剪切角φ仅与变量切屑厚度tc有关,tc稍微的波动就会引起剪切角φ的显著变化,从而影响参数C的计算值.以第1组数据为例,计算切屑厚度tc的微小波动对参数C的影响.把切屑厚度tc由0.106 mm改为0.096 mm,计算发现参数C由0.060 484变化为0.071 245,即切屑厚度tc变化0.01 mm可引起参数C变化1.20倍(表 5).由以上分析可以得到如下结论:1) 参数C的取值除了刀具参数、切削参数等定值影响外,主要还受到主切削力Fc、进给力Ft和切屑厚度tc的影响;2) 切屑厚度tc对参数C的最终计算值影响较大,尤其是当切屑厚度较小时,影响更为显著.
| 表 5 切屑厚度微小波动对参数C的影响 Table 5 The influence of micro fluctuation of chip thickness on the parameter C |
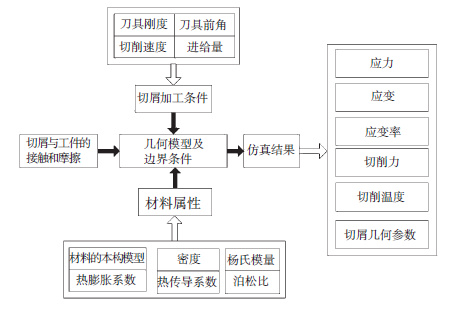
金属切削加工的有限元分析是一个复杂的过程,涉及到很多因素,在自由切削加工的有限元模型中做出如下假设[16]:1) 平面应变状态假设,当切削宽度是切削深度的5倍或大于5倍时,模型作为平面应变问题进行分析;2) 刀具的假设,由于刀具材料的弹性模量远大于工件材料的弹性模量,切削过程中刀具的弹性变形可以忽略,将刀具假设为刚体.基于以上假设建立了切屑成形的有限元仿真模型,有限元分析流程如图 3示.
|
图 3 切削加工有限元分析流程 Figure 3 The finite element analysis process of machining |
模型中工件材料的本构模型为本文已建立的J-C材料本构模型.但由于ABAQUS软件中的本构模型的参数C需要输入具体的数值,取表 3中22组试验的平均值,C为0.062.参考应变率为0.03,因此,J-C模型的具体形式如式(5) .本次建模仿真采用的是Euler方法,因此无需设置材料的切屑分离准则.
| $\begin{align} & \sigma =\left( 1240+270{{\varepsilon }^{0.36}} \right)\times \\ & \left[ 1+0.062\left( \ln \left( 1+\frac{{\dot{\varepsilon }}}{{{{\dot{\varepsilon }}}_{0}}} \right) \right) \right]\centerdot \left[ 1-{{\left( \frac{T-{{T}_{r}}}{{{T}_{m}}-{{T}_{r}}} \right)}^{1.26}} \right]. \\ \end{align}$ | (5) |
分析在ABAQUS/Explicit的热力耦合模块中进行.在通用有限元软件ABAQUS 6.10提供的ALE算法基础上开发了切屑成型的仿真模型,该模型无需设置材料分离准则,而且具有良好的收敛性,适用于连续型切屑形成过程的仿真分析.
在几何模型中,为了缩减计算时间,工件材料简化为1.2 mm×0.4 mm的长方形,单元格为4节点的平面应变热力耦合缩减积分单元CPE4RT,仅选择靠近切削刃位置进行刀具建模.材料的物理性能参数以及切削参数如表 6及表 7所示.
| 表 6 45CrNiMoVA和刀具的物理性能参数 Table 6 The physical property parameters of 45CrNiMoVA and cutting tool |
| 表 7 刀具几何参数和切削用量 Table 7 The cutting tool geometry parameter and cutting dosage |
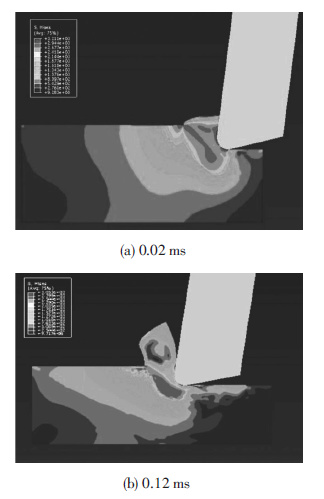
图 4(a)为初始切屑形成时的应力分布云图,最大应力位于第一变形区内,工件材料在第一变形区内发生塑性变形进而形成切屑.随着切屑的流出,因同前刀面发生摩擦而形成另一个高应力区域.同时,新生成的已加工表面同后刀面之间由于摩擦力的作用,也出现了应力集中的区域.
|
图 4 应力分布(切削参数:vc=10 m/min,f=0.1 mm/r) Figure 4 Stress distribution(cutting parameters: vc=10 m/min,f=0.1 mm/r) |
图 4(b)为稳态切削过程中的应力分布云图,最大应力位于第一变形区内.此外,由于刀-屑间的摩擦作用,刀-屑接触面间的应力值也达到最大值.由图 4(b)的应力分布可以看出,在稳态切削过程中,应力值基本达到稳定状态,随切削时间的增加,应力值没有明显变化.
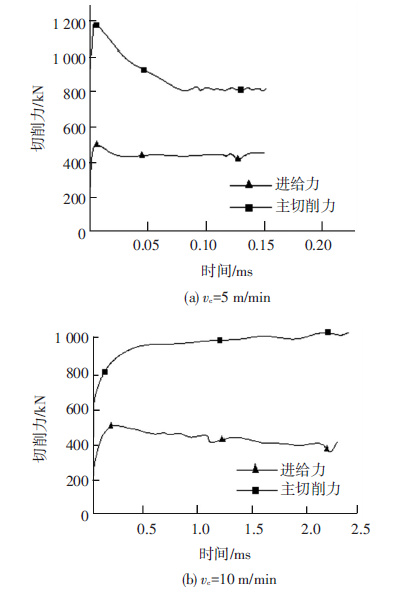
通过定义在刀具参考点上的反作用力,获得刀具上的切削力值,图 5给出了切削力在2 ms内的变化情况,可以看出,切削力在切削进行很短的时间内即达到稳定状态.
|
图 5 切削力随时间变化规律(f=0.1 mm/r) Figure 5 Low of cutting force variation with time(f=0.1 mm/r) |
提取出稳定状态时的切削力和切屑形态,并与相应的试验测得值进行对比发现:主切削力和切屑厚度的仿真预测值与试验测量值的误差在10%之内,而进给抗力误差较大,这是因为在仿真过程中刀具不存在磨损现象,而试验中刀具在较短时间内便会有磨损产生,导致仿真中的进给抗力与试验中的进给抗力明显不同.这是目前有限元仿真切屑形成过程普遍存在的问题.
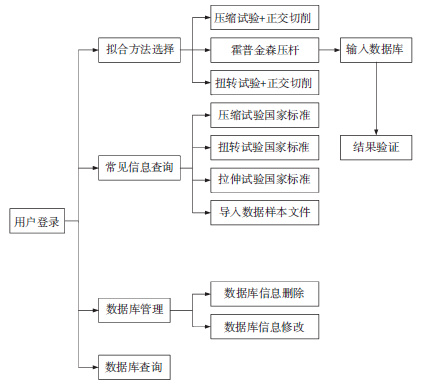
4 J-C材料本构集成建模系统 4.1 集成建模系统基本流程利用VB和C语言,开发了Johnson-Cook材料本构集成建模系统.本系统采用Johnson-Cook本构模型,利用Oxley切削理论模型、最小二乘法、多元非线性回归等算法和修改过的Boothroyd温度模型拟合材料本构方程中的参数[17],将试验原始数据与Johnson-Cook模型预测值进行对比,验证系统得到的本构方程的正确性.集成建模系统基本流程图如图 6所示.
|
图 6 集成建模系统基本流程图 Figure 6 Basic flow chart of integrated modeling system |
本文建立的集成建模系统有如下功能:
1) 系统可通过压缩试验数据拟合本构方程中的应变强化系数A、B、n,可通过压缩试验的外推值与直角自由切削试验数据拟合应变率强化系数C和温度软化系数m,并得到方程的预测值与试验值的对比图.
2) 在系统中输入霍普金森压杆试验、低温低应变率试验等试验数据,可以得到材料的本构模型参数,并得到方程的预测值与试验值的对比图.
3) 系统可将静态扭转试验和直角自由切削试验得到的较大应变与直角自由切削试验结合,拟合出材料的本构模型参数,并得到方程的预测值与试验值的对比图.
4) 本系统对所有用户开放数据库的查询功能,用户可以方便的查询到常见材料的本构模型,系统收录了目前文献中的部分材料本构模型.
5) 数据库的修改和删除.本系统对注册的用户开放此功能,用户可以根据自己的试验或需求来修改数据库中的参数.
6) 常见资料的查询.系统集成了压缩试验国家标准,扭转试验国家标准等常见的资料,用户可以根据自己的需要查询使用.
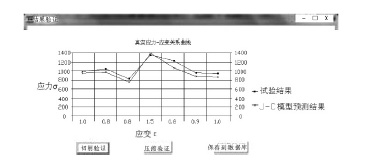
4.3 系统应用举例将静态压缩试验和直角自由切削试验结合,拟合材料本构方程,并进行验证和保存到数据库,来实现系统的操作.登录系统主页面,在界面选择“压缩+直角自由切削”,并通过xls文件将压缩试验的载荷与变形量数据导入到窗体中.由于试验的误差或其他影响,参数C的计算结果有可能为负值,因此参数C的显示是经过筛选的,将符合结果的显示出来,并在前面用下标标注是哪一组试验得到的结果.显示的部分除了J-C模型的5个参数外,还有计算的中间变量—最高温度和最大应变率,也一同显示在窗体的右下方,表示得到的模型的适用范围,同样是非常重要的参数.结果显示如图 7所示,到此,模型的拟合部分完成,之后进入模型的验证部分.本部分提供了切削试验验证和压缩试验验证两部分,系统会自动绘制以等效应变和等效应力为坐标的应力-应变关系曲线,将真实试验结果与用模型预测的结果绘于同一张表中,用户可直观地看到刚才计算得到的Johnson-Cook本构模型的精度.
|
图 7 J-C模型结果验证 Figure 7 Validation of J-C model results |
1) 本文通过准静态扭转试验和直角自由切削试验相结合的方法,建立了45CrNiMoVA 材料的Johnson-Cook材料本构模型,能满足高速切削仿真的要求,并准确反映材料在高应变率条件下的真实变形.
2) 利用建立的Johnson-Cook材料模型进行了45CrNiMoVA 材料的切削仿真,主切削力和切屑厚度的仿真预测值与试验测量值的误差在10%之内,模型的准确度较好.
3) 利用VB和C语言,成功开发了Johnson-Cook材料本构集成建模系统,可方便实现材料本构参数的拟合与查询.
| [1] |
LIST G, SUTTER G, BOUTHICHE A. Cutting temperature prediction in high speed machining by numerical modelling of chip formation and its dependence with crater wear[J]. International Journal of Machine Tools and Manufacture, 2012, 54 : 1 –9.
( 0) 0)
|
| [2] |
DA SILVA R B, MACHADO Á R, EZUGWU E O, et al. Tool life and wear mechanisms in high speed machining of Ti-6Al-4V alloy with PCD tools under various coolant pressures[J]. Journal of Materials Processing Technology, 2013, 213 (8) : 1459 –1464.
DOI: 10.1016/j.jmatprotec.2013.03.008 ( 0) 0)
|
| [3] |
曹自洋, 何宁, 李亮, 等. 高速切削钛合金Ti-6Al-4V切削的形成及其数值模拟[J]. 中国机械工程, 2008, 19 (20) : 2450 –2453.
CAO Ziyang, HE Ning, LI Liang, et al. Chip formation and its numerical simulation in high speed cutting of Ti6Al4V alloy[J]. China Mechanical Engineering, 2008, 19 (20) : 2450 –2453.
( 0) 0)
|
| [4] |
杨柳, 杨博. 中碳钢热拉伸流变应力本构模型[J]. 浙江工业大学学报, 2008, 1 : 112 –115.
YANG Liu, YANG Bo. Rheological stress constitutive model of medium carbon constructional quality steels under thermal tension[J]. Journal of Zhejiang University of Technology, 2008, 1 : 112 –115.
( 0) 0)
|
| [5] |
解丽静, 郑丹, SchmidtC, 等. 基于“差分”磨损模型的车削刀具磨损仿真预测研究[J]. 工具技术, 2005, 41 : 17 –20.
XIE Lijing, ZHENG Dan, SCHMIDT C, et al. Study on prediction of tool wear in turning operation based on “Differential” wear rate model[J]. Tool Technology, 2005, 41 : 17 –20.
( 0) 0)
|
| [6] |
黄志刚, 柯映林, 王立涛. 金属切削加工的热力耦合模型及有限元模拟研究[J]. 航空学报, 2004, 25 (4) : 317 –320.
( 0) 0)
|
| [7] |
王洪祥, 高石, 黄志群, 等. KDP晶体超精密切削过程中等效应力和应变分析[J]. 材料科学与工艺, 2006, 16 (3) : 326 –334.
WANG Hongxiang, GAO Shi, HUANG Zhiqun, et al. Analysis on equivalent stress and strain of KDP crystals in ultra 2 precision machining process[J]. Materials Science and Technology, 2006, 16 (3) : 326 –334.
( 0) 0)
|
| [8] |
常艳艳, 孙涛, 李增强. 硬铝合金超精密车削残余应力的仿真及试验[J]. 哈尔滨工业大学学报, 2015, 47 (7) : 41 –46.
CHANG Yanyan, SUN Tao, LI Zengqiang. Simulation and experiments of residual stresses on ultra-precision turning of hard aluminum alloy[J]. Journal of Harbin Institute of Technology, 2015, 47 (7) : 41 –46.
( 0) 0)
|
| [9] |
严宏志, 龚黎军. 20CrMo材料本构模型及有限元模拟[J]. 中南大学学报, 2012, 43 (11) : 4268 –4273.
YAN Hongzhi, GONG Lijun. Consititutive model and finite element simulation of 20CrMo material[J]. Journal of Central South University(Science and Technology), 2012, 43 (11) : 4268 –4273.
( 0) 0)
|
| [10] |
JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strain, high strain rates and high temperatures[J]. The Hague, Nether Lands, 1983 : 541 –547.
( 0) 0)
|
| [11] |
HAMDAN A, SARHAN A A D, HAMDI M. An optimization method of the machining parameters in high-speed machining of stainless steel using coated carbide tool for best surface finish[J]. The International Journal of Advanced Manufacturing Technology, 2012, 58 (1/2/3/4) : 81 –91.
( 0) 0)
|
| [12] |
黄志斌, 万敏, 伍惠, 等. TC4钛合金神经网络本构模型及在有限元模拟中应用[J]. 塑性工程学报, 2013, 20 (1) : 89 –94.
HUANG Zhibin, WAN Min, WU Hui. Constitutive model of Ti-6Al-4V alloy based on artificial neural network and its application on FEM simulation[J]. Journal of Plasticity Engineering, 2013, 20 (1) : 89 –94.
( 0) 0)
|
| [13] |
SHI Y, WANG M, WANG Y. Experimental and constitutive model study of structural steel under cyclic loading[J]. Journal of Constructional Steel Research, 2011, 67 (8) : 1185 –1197.
DOI: 10.1016/j.jcsr.2011.02.011 ( 0) 0)
|
| [14] |
陈姗姗, 李宏伟, 杨合. 弹粘塑性晶界变形损伤本构模型[J]. 塑性工程学报, 2014, 21 (2) : 13 –19.
CHEN Shanshan, LI Hongwei, YANG He. Elastic-viscoplastic constitutive model of grain boundary deformation and damage[J]. Journal of Plasticity Engineering, 2014, 21 (2) : 13 –19.
( 0) 0)
|
| [15] |
YE G G, XUE S F, JIANG M Q, et al. Modeling periodic batic shear band evolution during high speed machining Ti-6Al-4V alloy[J]. International journal of plasticity, 2013, 40 : 39 –55.
DOI: 10.1016/j.ijplas.2012.07.001 ( 0) 0)
|
| [16] |
SU G, LIU Z. Wear characteristics of nano TiAlN-coated carbide tools in ultra-high speed machining of AerMet100[J]. Wear, 2012, 289 : 124 –131.
DOI: 10.1016/j.wear.2012.04.005 ( 0) 0)
|
| [17] |
JIN D, LIU Z. Effect of cutting speed on surface integrity and chip morphology in high-speed machining of PM nickel-based superalloy FGH95[J]. The International Journal of Advanced Manufacturing Technology, 2012, 60 (9/10/11/12) : 893 –899.
( 0) 0)
|
 2016, Vol. 24
2016, Vol. 24


