半导体光催化技术是利用半导体材料吸收光子能量产生电子-空穴对,从而与目标物进行氧化-还原反应,以实现净化水体、裂水制氢等应用研究目的.目前,二氧化钛(Titanium dioxide, TiO2)是最接近商业化的光催化材料,然而,其禁带宽度约为3.2 eV,对应吸收波长落在仅占太阳能光谱4%的紫外光区域,因此,光子能量利用率低是困扰TiO2工业化应用发展的主要问题[1].由于到达地球表面太阳光谱中可见光所占比例接近一半,因此,设计、开发高活性且具有可见光响应特性的新型光催化剂材料是目前半导体光催化技术研究领域热点之一.
磷酸银(Silver phosphate, Ag3PO4)是一种具有高催化活性的可见光催化材料,在波长小于530 nm光源照射下,Ag3PO4能够表现出极强的光氧化能力,可高效降解有机污染物,量子效率超过90%[2].然而,稳定性能较差,光催化循环利用率低是Ag3PO4研究过程中需要解决的主要问题[3].研究人员为此已做了大量工作,但多数集中在Ag3PO4稳定性能优化手段研究方面[4-5],而涉及Ag3PO4稳定性能的理论研究却鲜有报道.此外,由于Ag3PO4热稳定性差,研究人员很难通过实验手段准确获得描述Ag3PO4熵、焓、自由能等热力学性质的相关信息.基于密度泛函理论的第一性原理计算已被成功用于各类功能材料的理论研究工作[6-7],同时,已有报道证实这一方法能够用于Ag3PO4光催化活性的理论研究,如UMEZAWA等[8]采用密度泛函理论分析了Ag3PO4优异光催化活性原因;朱等[9]结合密度泛函理论与LDA+U,对比分析了U值选择对Ag3PO4电子结构与光催化活性计算结果的影响.
本文将采用基于密度泛函理论(DFT)的第一性原理,采用规范-守恒赝势平面波方法,通过对Ag3PO4 Mulliken布居、能带结构、态密度以及声子谱、声子态密度的计算分析,从化学结构与电子结构角度出发,探讨分析Ag3PO4稳定性能较差的本质原因,并在此基础上,对Ag3PO4晶体体系的热力学性质,如熵、焓、自由能以及等容热容随温度的变化规律进行深入研究.上述研究结果对于进一步优化Ag3PO4稳定性能,缩短其在光催化研究领域实际应用进程将有一定的指导意义.
1 理论模型与计算方法 1.1 模型构建Ag3PO4晶体为体心立方,属P4-3n空间群(218).模型构建所用晶格常数与原子分数坐标分别为:a=b=c=0.600 4 nm,α=β=γ=90°;Ag (0.25 0 0.5),P (0 0 0),O (0.148 0.148 0.148)[10],晶胞结构如图 1所示,其结构组成由独立规则的PO4构成体心立方晶格,6个Ag原子分布在12对相邻PO4四面体的对称点上.

|
图 1 体心立方Ag3PO4晶胞结构示意图 Figure 1 Unit cell structure of cubic Ag3PO4 |
计算工作采用基于密度泛函理论的规范-守恒赝势平面波方法,电子交换相关项采用杂化泛函PBE0计算.电子波函数取截断能Ecut为750 eV的平面波基矢展开,第一布里渊区k点分割设置为4×4×4格点.电子结构自洽精度为1.0×10-6 eV/atom.选取Ag-4d105s1,P -3s23p3,O-2s2 2p4组态电子作为价电子,其余轨道电子作为苾电子进行计算.几何优化过程收敛标准设置如下:每个原子上最大能量变化为1.0×10-5eV,原子间最大相互作用力为0.03 eV/Å,最大压力0.05 GPa,原子最大位移为1.0×10-3 Å.通过线性响应方法,计算Ag3PO4的声子谱.
2 理论模型与计算方法 2.1 结构优化几何优化后的Ag3PO4晶格结构参数如表 1所示.从表 1可以看出,优化后晶格参数与实验值相比略有增加,由此产生误差1.15%,小于允许误差2%,说明本研究所选计算方法具有较好的准确性和可靠性.
| 表 1 Ag3PO4晶格参数统计表 Table 1 Crystal lattice constants for Ag3PO4 |
Mulliken布居分析常被用于研究电荷在各原子间分布情况以及不同原子间化学健性质[11-12],表 2为Ag3PO4 Mulliken电荷布居计算结果.在Ag3PO4晶体体系中,每个O原子可获得0.98个价电子,而P,Ag原子均失去部分价电子,其中,Ag原子失去价电子数量(0.58)小于P原子(2.18),说明Ag原子失电子能力弱于P原子.
| 表 2 Ag3PO4的Mulliken电荷布居 Table 2 The calculated Mulliken charge population of Ag3PO4 |
表 3汇总了Ag3PO4 Mulliken健布居数以及不同原子间化学健健长.通常,键布居数为0~1间的数值,其值越接近于0说明化学健性质越接近于离子健,反之则说明共价健性质高;此外,健布居数的正负性分别代表电子处于成健轨道与反键轨道[13].从表 3可以看出,P-O与Ag-O健布居值分别为0.62、0.13,由于均为正值,表明电子均处于成键轨道;而P-O健布居值明显高于Ag-O健(0.62>0.13),说明P-O间共价健性质更强,再加上P-O健长(0.154 6)小于Ag-O健长(0.240 7),说明与Ag-O相比,P-O间结合更加紧密,原子相互间重叠程度更大,形成的共价健牢固性更高,即P-O健更加稳定.此外,由于O-O健布居数为负值(-0.13),说明O原子间由于距离较远,电子云被拉长,导致电子跃迁至反键轨道,但O原子间依然存在一定程度共价健性质的健合力.
| 表 3 Ag3PO4的Mulliken健布居数 Table 3 The calculated Mulliken bond population of Ag3PO4 |
综上述分析可知,P-O间牢固共价健的形成使P-O结合更加紧密,P、O原子在Ag3PO4晶体中能够形成如图 1箭头所指的PO4四面体,而位于四面体顶点O原子间共价健合力的存在又进一步确保PO4四面体结构更加稳定.由于PO4四面体的存在会在一定程度上弱化Ag-O间健合力,因此, 会导致Ag+在Ag3PO4晶体中处于亚稳态.
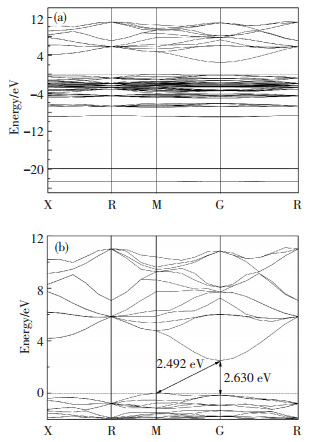
2.3 能带结构及态密度分析图 2(a)为Ag3PO4能带结构图,0点为体系费米能级(EF=0 eV),费米能级附近能带结构如图 2(b)所示.由于价带顶位于布里渊区M点,而导带底位于布里渊区G点,说明Ag3PO4属于间接带隙半导体,这与文献[2]的研究结论相符.但本研究工作计算结果间接带隙为2.492 eV,直接带隙为2.630 eV,上述数值均高于文献[2]的实验测试与计算结果,原因或源于杂化泛函PBE0的采用以及选用高的截断能Ecut.此外,根据图 2(a)可以看出,导带在2~11 eV能量区间起伏程度远高于价带,尤其位于导带低部曲线具有明显抛物线形态,这充分说明跃迁至导带的激发电子具有较轻的有效质量,易于在Ag3PO4内部迁移,这与UMEZAWA等[8]通过公式得到的结论是一致的.利用态密度分析可以获取各原子电子态对导带与价带的贡献信息.
|
图 2 Ag3PO4能带结构图(a)与费米能级附近放大能带结构图(b) Figure 2 Band structure of Ag3PO4 (a) and a magnified view of band structure near the Fermi level (b) |
图 3给出了Ag3PO4总态密度与不同原子亚层轨道态密度分布情况.在价带低能区间(E<-15 eV),其态密度主要由O 2s、P 3s以及P 3p态构成,较低能区间(-15 eV≤E<-5 eV)主要由O 2p、P 3s以及P 3p态构成,而在近费米能级价带区(-5 eV≤E<0),则主要由O 2p与Ag 4d态构成,P 3p贡献很少,可忽略;另一方面,导带靠近费米能级区(0<E≤7 eV)的态密度主要由Ag 5s态贡献,P与O的s、p轨道电子贡献几乎不存在,而导带高能区(7 eV<E≤15 eV)的态密度则由Ag 5s、Ag 5p以及少量P 3p构成.

|
图 3 Ag3PO4总态密度(a)与P原子(b)、O原子(c)、Ag原子(d)分态密度图 Figure 3 The total and partial electronic density of states for Ag3PO4 (a), P atom (b), O atom (c), and Ag atom(d), respectively |
结合图 2,图 3可知,费米能级附近的总态密度几乎完全来自于O 2p, Ag 4d以及Ag 5s态密度的贡献,这与Ag3PO4Mulliken电荷布居分布情况是相符的,同时亦说明Ag3PO4的载流子输送性质主要由O 2p, Ag 4d以及Ag 5s态电子决定.此外,价带顶处Ag 4d与O 2p态密度存在部分重叠现象,说明Ag 4d与O 2p轨道之间存在一定程度的杂化作用,而在价带低能区,O 2s与P 3p态密度高度重合,说明O 2s与P 3p轨道杂化非常强烈,这进一步表明P-O间作用程度要高于Ag-O间.Ye等认为P-O间牢固共价健的存在会抑制Ag 4d轨道与O 2p轨道的杂化,从而减少导带中d轨道成分,使导带底只存在宽范围分散的Ag 5s-Ag 5s杂化轨道,进而造成电荷分布离域性增强[2].因此,Ag3PO4特殊的能带结构易导致跃迁至导带的光生电子在材料内部具有较强迁移能力,易于扩散.当亚稳态Ag+遇到光生电子时,很容易摆脱O2-束缚生成单质银,Ag3PO4因此表现出光不稳定性.
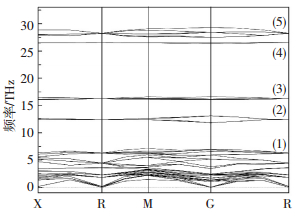
2.4 声子谱与声子态密度分析通过对晶体材料声子谱研究可以明确材料是否具有动力学稳定性特征,同时,利用声子谱中谱线重叠以及各原子声子态密度峰的位置可反映出原子间是否存在相似或相同的振动状态,从而能够推断出原子间是否存在相互作用以及作用力的强弱[14].Ag3PO4的声子谱如图 4所示.由于图 4中不存在虚频,说明Ag3PO4晶体具有动力学稳定性特征.此外,由于Ag3PO4原胞内有16个原子,故应具有48个简正振动模,包括3个声学模与45个光学模.分析Ag3PO4声子谱计算结果可知,在0~30 THz范围内有48条谱线,说明本研究计算结果与理论相符.
|
图 4 Ag3PO4在0 GPa条件下的声子谱 Figure 4 Phonon spectrum of Ag3PO4 under 0 GPa condition |
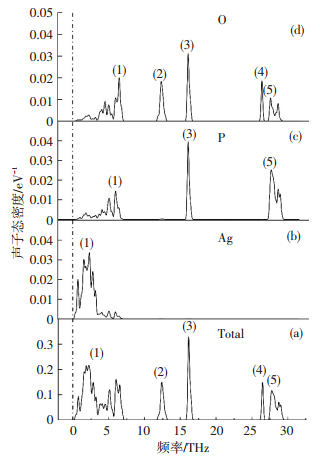
从图 4还可以看出,Ag3PO4在0~30 THz的声子谱主要由5组谱带构成,其中,第1组谱带(0~7.5 THz)包括3个声学模与27个光学模,而第2组(11.5~13.2 THz)、3组(16~17 THz)、4组(26~27 THz)、5组(27.5~30 THz)谱带则分别由4,6,2,6个光学模组成.由于各谱带内谱线均出现不同程度的重叠现象,说明Ag3PO4晶体体系中各原子间应具有相同或相近的振动状态,这进一步证实了原子间相互作用力的存在.另一方面,对比分析Ag3PO4声子态密度与各原子声子分态密度可知(图 5),P,O原子在第1,3,5谱带内均出现声子态密度峰高度重合现象,说明P,O原子具有相同的振动状态,二者之间必然存在强的作用力;而Ag原子的声子态密度峰均位于低频区的第1谱带,且与其他原子重叠范围较小,说明Ag原子与其他原子之间作用力较弱,上述分析结果与前面研究结论是吻合的.此外,Ag3PO4声子谱(图 4)中各谱带间禁带的存在说明该晶体材料的振动模具有非连续振动特征,禁带区所对应的振动频率在晶体中不会产生.
|
图 5 Ag3PO4总声子态密度(a)与Ag原子(b)、P原子(c)、O原子(d)声子分态密度图 Figure 5 The total and partial phonon density of states for Ag3PO4 (a), Ag atom (b), P atom (c), and O atom (d), respectively |
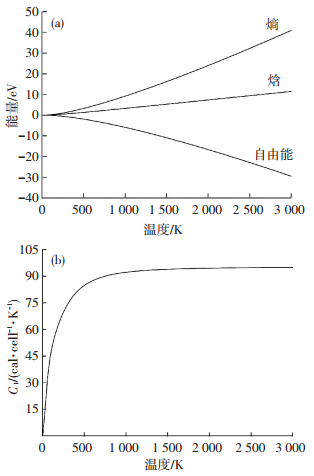
Ag3PO4晶体体系熵、焓、自由能以及等容热容随外界温度的变化规律,结果如图 6所示.当温度低于300 K时,Ag3PO4晶体体系的熵、焓、自由能变化均较为平缓,说明300 K以下的Ag3PO4具有较好热稳定性.进一步升高温度时,体系熵、焓、自由能表现出不同的变化趋势:熵值增加明显,热焓增加较缓,而自由能出现下降.考虑到低温条件下,组成材料的分子通常处于晶格内固定位置,其振动、转动以及移动都相对较弱,晶体体系能量变化很小,因此,晶体体系的熵、焓、自由能变化均不明显;而温度逐渐增加时,组成材料的分子振动频率加快,分子无序性增加,当分子不再束缚于某一具体位置而可以自由转动和移动时,体系熵值与热焓均会增加.而具体到Ag3PO4晶体,其体系内部P-O牢固共价键的形成还会导致Ag3PO4粒子相互接近时产生极化作用而影响整个晶体体系能量,因此,熵值与热焓均表现出一种非线性增加趋势.对体系自由能,由于其值=U(体系内能)-TS(熵),U=△H-p△V,因此,当温度增加时,体系内能(焓变)会落后于熵变,从而导致自由能随温度增加而减小.
|
图 6 Ag3PO4晶体体系(a)熵、焓、自由能与(b)热容随温度变化曲线图 Figure 6 The entropy, enthalpy, free energy (a) and heat capacity (b) of Ag3PO4 for various temperature |
等压条件下Ag3PO4晶体体系等容热容CV与温度关系曲线如图 6(b)所示.随温度增加,CV变化表现出3个阶段:1)0~300 K,CV值迅速增加;2)300~1 200 K,CV增加趋势减缓;3)T>1 200 K,CV趋于恒定.上述CV的变化趋势可以依据晶格热振动理论予以解释.通常,固体热容主要由晶格热振动能量与电子热运动能量组成.低温阶段,晶格热振动能量与温度符合T3幂次规律,电子热运动能量与温度也呈线性关系;而随温度增加,电子热运动能量对固体热容贡献会逐渐减弱,当温度超过材料熔点时,这一能量甚至可忽略不计,此时固体材料热容主要由晶格振动能量决定[15].由于Ag3PO4熔点约为1 122 K,因此,当温度达到1 200 K时,Ag3PO4已由固态转变为液态,其分子也早已离开晶格中固定位置,相应振动能量亦不再有所变化,因此,晶体体系的CV接近恒定数值,经计算约为93 cal/cell·K.
3 结论1) Ag3PO4晶体结构中稳定PO4四面体存在能够弱化Ag-O间健合力,使Ag+处于亚稳态;Ag+接触光生电子时,易摆脱O2-束缚生成单质银,Ag3PO4因而表现出光不稳定性.
2) Ag3PO4晶体具有动力学稳定性特征,其振动模表现出非连续性特征.
3) 300~3 000 K范围内,Ag3PO4晶体体系熵、焓随温度增加而呈非线性增加,自由能下降;等容热容CV在1 200 K时达到恒定,约为93 cal/cell·K.
| [1] | KEANE D A, MCGUIGAN K G, IBÁÑEZ P F, et al. Solar photocatalysis for water disinfection: materials and reactor design[J]. Catalysis Science & Technology, 2014, 4 (5) : 1211 –1226. |
| [2] | YI Z G, YE J H, KIKUGAWA N, et al. An orthophosphate semiconductor with photooxidation properties under visible-light irradiation[J]. Nature Material, 2011, 9 (7) : 559 –564. |
| [3] | CHEN X J, DAI Y Z, WANG X Y. Methods and mechanism for improvement of photocatalytic activity and stability of Ag3PO4: A review[J]. Journal of Alloys and Compounds, 2015, 649 : 910 –932. DOI: 10.1016/j.jallcom.2015.07.174 |
| [4] | LIU L, QI Y, LU J, et al. A stable Ag3PO4@g-C3N4hybrid core@shell composite with enhanced visible light photocatalytic degradation[J]. Applied Catalysis B: Environmental, 2016, 183 : 133 –141. DOI: 10.1016/j.apcatb.2015.10.035 |
| [5] | CAI L, LONG Q Y, YIN C. Synthesis and characterization of high photocatalytic activity and stable Ag3PO4/TiO2 fibers for photocatalytic degradation of black liquor[J]. Applied Surface Science, 2014, 319 : 60 –67. DOI: 10.1016/j.apsusc.2014.07.103 |
| [6] | HUANG D, PERSSON C. Photocatalyst AgInS2 for active overall water-splitting: A first-principles study[J]. Chemical Physics Letters, 2014, 591 (3) : 189 –192. |
| [7] | 秦永和, 乔英杰. Sm、La掺杂TiAl结构和性能的第一性原理计算[J]. 哈尔滨工业大学学报, 2015, 47 (5) : 123 –128. QIN Yonghe, QIAO Yingjie. The first principle calculation for structure and mechanical property of Sm, La doping with TiAl[J]. Journal of Harbin Institute of Technology, 2015, 47 (5) : 123 –128. |
| [8] | UMEZAWA N, OUYANG S, YE J H. Theoretical study of high photocatalytic performance of Ag3PO4[J]. Physical Review B, 2011, 83 (3) : 287 –292. |
| [9] | MA X G, LU B, LI D, et al. Origin of photocatalytic activation of silver orthophosphate from first-principles[J]. The Journal of Physical Chemistry C, 2011, 115 (11) : 4680 –4687. DOI: 10.1021/jp111167u |
| [10] | NG H N, CALVO C, FAGGIANI R. A new investigation of the structure of silver orthophosphate[J]. Acta Crystallographica Section B, 1978, 34 (3) : 898 –899. DOI: 10.1107/S0567740878014570 |
| [11] | MAYER I, RÄTHER G, SUHAI S. Wannier-type orbitals derived from Mulliken's population analysis[J]. Chemical Physics Letters, 1998, 293 (1) : 81 –89. |
| [12] | 王宏明, 郑瑞, 李桂荣, 等. 第一性原理研究MgZn2相的电子结构及磁性质[J]. 无机化学学报, 2015, 31 : 1 –9. WANG H M, ZHENG R, LI G R, et al. First-principles research on the electronic and magnetic properties of MgZn2 phase[J]. Chinese Journal of Inorganic Chemistry, 2015, 31 : 1 –9. |
| [13] | SEGALL M D, SHAH R, PICKARD C J, et al. Population analysis of plane-wave electronic structure calculations of bulk materials[J]. Physical Review B, 1996, 54 (23) : 16317 –16320. DOI: 10.1103/PhysRevB.54.16317 |
| [14] | LI H, SUN G D, DENG J L, et al. Phonon and electronic properties of Ti2SiC from first-principles calculations[J]. Solid State Communications, 2015, 204 : 37 –40. DOI: 10.1016/j.ssc.2014.12.010 |
| [15] | M.玻恩, 黄 昆. 晶格动力学理论. 北京: 北京大学出版社, 1989 . |
 2016, Vol. 24
2016, Vol. 24


