航空整体结构框架件尺寸大、结构复杂、壁薄、刚度差,在生产制备过程中加工质量和精度很难控制, 容易发生变形,普遍存在的加工变形已是数控加工领域的一大难题[1-4].
国内学者在铝合金材料性能方面做了大量的研究,陈军等[5]研究了铝合金板材疲劳性能和裂纹扩展速率.张新明等[6]采用光学金相、示差扫描量热分析、扫描电镜、室温拉伸及断裂韧性实验,研究了多级固溶处理对7050铝合金强度和断裂韧性的影响.北京航空航天大学的梅中义和王巧运等人以飞机弧形薄壁件为研究对象,对其数控加工变形情况进行了系统研究,并从构件初始应力分布、切削力、装夹力3个方面分析了导致构件最终变形的原因, 提出了相应的解决方案[7-9].中南大学、山东大学等院校也开展了薄壁框架件变形影响的研究[10-12],包括振动时效和数值仿真预测.
导致航空结构件发生变形的主要原因有:铝合金厚板初始残余应力释放、铣削加工引入加工应力.针对铝合金薄壁框架件应力变形问题,国内外学者做了大量的研究工作.国内哈尔滨工业大学的林爱琴[13]等人研究了通过残余应力的变化规律及工件变形情况有效控制工件变形的解析方法,获得最小变形时的最佳加工方法,对控制工件变形具有一定的指导意义.浙江大学的成群林等[14]运用有限元方法研究铝合金高速铣削加工,利用建立面向铣削加工的有限元模型,模拟得到航空铝合金铣削加工时的切削力、切削应力及温度,为铝合金切削加工的工艺参数优化、刀具的优选和工艺规划提供了参考.Nervi[15]构建了毛坯初始残余应力引起加工变形的数学预测模型,指出零件的最终变形情况与毛坯初始应力的分布状态与形状有关.Young[16]采用数值模拟与铣削相结合的方法研究了铣削加工引入的残余应力对加工变形的影响,指出加工引入的残余应力与变形与刀尖圆弧半径和切削刃钝圆半径密切相关.Imed等[17]建立了可以预测铝合金高速铣削过程中铣削力与铣削热的模型,研究发现,由该模型预测的结果与实验结果吻合良好.Weinert等[18-19]等学者运用有限元方法对构件的加工过程进行了数值计算分析.Robinson等[20]运用中子衍射技术对7449铝合金进行了面铣削加工应力测试,并对其加工前后的应力场状况进行了仿真与对比,研究了表面铣削加工应力场重组,认为加工前后的应力场具有相似性.本文通过X射线衍射实验测得铝合金厚板的表面初始残余应力及加工应力,利用层削法实验测得内部沿厚度方向上的初始残余应力,分析了实验中初始残余应力与铣削加工应力分别对铝合金薄壁框架件形变的影响[21],并在此基础上构建了构件变形的解析表达方法.
1 力学模型构建厚板加工为薄壁框架件后的变形以弯曲为主,如果壁厚不均匀,则可能出现弯扭结合的变形情况,本文仅考虑壁厚均匀的情况,这在加工实验中可以保证,不影响建模的准确性.首先,由于厚板制备后在内部形成的是一种“外压内拉”的平衡应力场,在材料去除后,框架中形成的空槽导致加工前的平衡态应力场的破坏,致使弯曲后的另一个平衡态形成,类似在槽壁上均布着的残余应力,在这种力的作用下,构件产生弯曲.其次,加工后的加工应力附着在加工表面层,该层深度很小,其均布于加工面且强度很大,在这种力的作用下,构件也能形成弯矩产生弯曲.分析可知,影响构件变形的两个主要因素是初始应力场分布和加工应力分布,将其作为主要参数构建变形函数对构件变形进行计算.
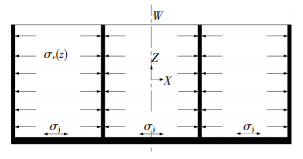
薄壁框架件的应力分布如图 1所示,薄壁框架件由于其内部材料的去除导致构件弯曲变形,侧壁及底部上的加工应力为加剧弯曲变形提供了动力.根据材料力学的弯曲变形模型可得,构件在薄壁处形成的弯矩大小和构件的抗弯截面强度直接影响构件的变形.图 1中σc(z)为初始应力,初始应力是继承了厚板制备时的残余应力,其计算过程参见文献[21-23],本处不再赘述;σj为铣削加工应力,由于其影响深度浅(在表层100 μm以内),可以将其视为常数分布于加工层剖面上.W为特定形体下抗弯截面系数,可以通过Marc有限元建立相似形态的构件受力模型,对其施加弯矩并进行形变的分析,以此计算出特定受力状态下形体的抗弯截面系数.
|
图 1 薄壁框架件应力模型 Figure 1 Thin wall component model |
图 1显示了薄壁框架件沿X方向上的受力状况,Y方向的变形机制与其一致.造成构件弯曲变形的原动力主要有两个,即分布于断面的初始残余应力和铣削加工应力.由于薄壁框架件的结构特点,造成了构件不对称弯曲空间的条件,使得初始残余应力促进构件的变形.初始残余应力沿断面分布后在对称面YZ平面上可以形成弯矩Mc(z),即
| ${M_e}\left( z \right) = \int\limits_{{z_{_c1}} \to 0 \to {z_2}} {{\sigma _{\rm{c}}}\left( z \right) \cdot l \cdot z{\rm{d}}z.} $ | (1) |
式中:l为框架件内宽度,mm;z1,z2为框架对称与弯曲中性面的高度,正负号由坐标决定,mm.
铣削加工应力分布在加工面上,作用在薄壁上的加工应力无论强度多高,由于其作用方向在抗弯截面法向上,因此, 其对变形的影响很小,可以不予考虑.而作用在构件底面上的加工应力σj则完全不同,其对构件的变形不可忽略.加工应力在构件底部也能形成弯矩Mj,并促使构件变形,由图 1模型分析可知,
| ${M_j} = \int\limits_0^{{m_1}} {{\sigma _{\rm{j}}} \cdot W{\rm{dz}}{\rm{.}}} $ | (2) |
式中:W为抗弯截面系数,mm3;m1为实验确定加工应力层厚度,mm.
由于框架件底部变形,加工应力形成的弯曲力臂会骤然增大,从而形成加工应力弯曲与初始残余应力弯曲的互促式的变形形式,使得薄壁框架件变形增大.薄壁框架件的初始应力触发了加工应力对构件变形的作用,影响薄壁件变形的弯矩变为初始应力与加工应力所形成的总弯矩.
| ${M_{{\rm{total}}}} = {M_{\rm{j}}} + {M_{\rm{c}}}\left( z \right).$ | (3) |
构件中心最大变形为
| $\xi = \int {\frac{{{M_{{\rm{total}}}} \cdot L}}{{12EI}}{\rm{d}}x} .$ | (4) |
式中:L为构件长度,mm;E为弹性模量,MPa;I为惯性矩,mm3;
由力学模型分析可知,影响构件弯曲的总弯矩的大小取决于初始应力分布和加工应力强度.
2 实验与分析由于构件加工后改变了板坯几何尺寸和初始应力分布,且还有附着的外场加工应力的影响,框架内应力分布差异比较复杂,构件的变形通过函数直接解析很难获得.因此,可以通过实验的方法,首先获得应力-变形的分布状况,再构建适合这类构件的解析函数,以确保函数预测的准确性.
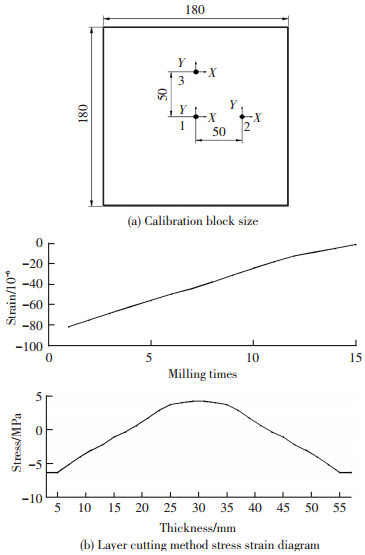
2.1 初始应力测试实验实验采用的材料是7075铝合金厚板,经过T651处理,板坯尺寸500 mm×230 mm×60 mm.首先获得铣削前厚板初始应力,由X射线衍射法测得其表面应力强度,如图 2所示.图 2(a)为初始应力标定块的尺寸以及测试点位置.测得标定块中间区域X方向平均应力为-10 MPa.
|
图 2 层削法应力测试 Figure 2 Removal layer method for stress |
铝合金厚板内部残余应力通过层削法沿厚度方向按照一定增量厚度,通过铣削加工剥除带有应力的厚度层,从而使试样基体应力平衡状态发生改变而变形,将测得的变形反求计算出剥离层应力值,获得构件初始应力分布函数σc(z).图 2(b)为退火板层削法实验应力应变图, 可以看到,铝合金厚板沿厚度方向残余应力分布,应力值在±5 MPa之间.
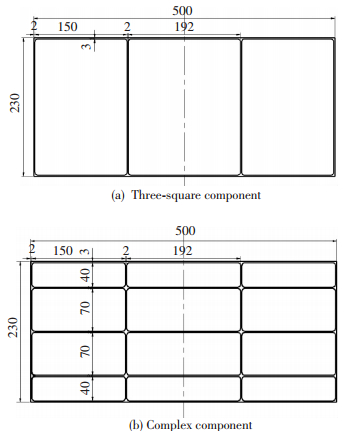
2.2 加工应力测试加工应力是在切削力和切削热的共同影响下产生的.根据上述初始应力测试可知,厚板在制备后残余应力水平被控制在一个较低的水平,但仍然在结构上保有一定强度的应力能,这部分能量在铣削加工后将会得到进一步释放,其释放的多少与变形有直接关系.铣削实验是将铝合金厚板分别各加工成3块三口型和复杂框架型框架件,共计6块试样.铣刀直径为16 mm,铣削后形状如图 3所示,三口型和复杂框架型框架件内框深度均为54 mm,底部厚度均为6 mm,测量表面加工应力的仪器为加拿大Proto公司生产X射线衍射仪,测量构件变形所用仪器为三坐标测量仪.铣削加工参数详见表 1.
|
图 3 铣削后框架件图 Figure 3 Component after milling |
| 表 1 铣削加工参数 Table 1 Milling of experiment |
铣削加工前后均采用X射线应力测试仪对表面应力进行了测试,测试结果见表 2.在如表 2所示工况下,6块试样在加工前后测得的应力值,由于加工应力作用的层深很小(通常为100 μm以内),模型中近似认为在这个层深内加工应力为均值.在初始应力及加工应力相似情况下,三口型的框架件变形与复杂框架件的变形不一样.框架件结构形式不同对加工后的变形存在影响.分析认为,由于不同的框架件结构有着不同的抗弯截面系数,即在不同的外场应力作用环境下,框架件的变形会有所差异.
| 表 2 应力测试 Table 2 Stress measurement |
解析模型解决的最大问题就是在已知应力测试数据的基础上,能够获得构件的最大变形范围,可在板坯未加工前就可以对其变形进行预先估测.
如表 2所示,将实验测得的底部两个极值应力代入式(2),通过积分即可求得总弯矩.
| $\begin{array}{l} 三口型:\left\{ \begin{array}{l} {M_{{\rm{zs1}}}} = 59920{\rm{N}} \cdot {\rm{mm;}}\\ {M_{{\rm{zs2}}}} = 135144{\rm{N}} \cdot {\rm{mm}}{\rm{.}} \end{array} \right.\\ 复杂框架:\left\{ \begin{array}{l} {M_{{\rm{zd1}}}} = 118176{\rm{N}} \cdot {\rm{mm;}}\\ {M_{{\rm{zd2}}}} = 265896{\rm{N}} \cdot {\rm{mm}}{\rm{.}} \end{array} \right. \end{array}$ |
式(2)中的抗弯截面系数W由有限元仿真计算得到:
| $\left\{ \begin{array}{l} {W_{{\rm{zs}}}} = 3745{\rm{m}}{{\rm{m}}^3}, \\ {W_{{\rm{zd}}}} = 7386{\rm{m}}{{\rm{m}}^3}. \end{array} \right.$ |
式中:zs代表三口型框架件;zd代表复杂型框架件.
总弯矩是由初始应力产生的弯矩和加工应力产生的弯矩共同作用的结果,初始应力弯矩可由实验测得的初始应力代入式(1)求得.比较总弯矩与初始应力弯矩即可得到加工应力弯矩.
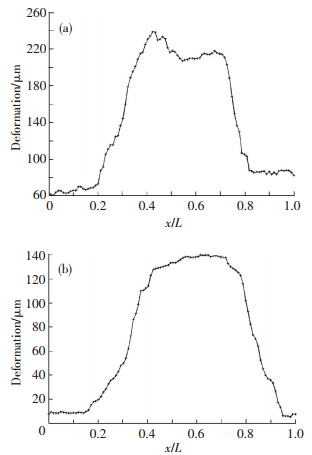
图 4指出了加工后构件表面形变分布,通过将加工前后的变形实验数据经过最小二乘法处理,得到构件的真实变形挠度.图 4显示构件在加工后呈现凸状变形,三口型框架比复杂框架变形要略大.
|
图 4 构件变形 Figure 4 Deformation of component:(a) deformation of three-square component; (b) deformation of complex component |
表 3给出了试样的实验和计算数据,包括不同构件形状和不同热处理工艺,可以看出:计算模型通过应力标定范围给出了一个变形可能波动的范围,而实验值基本都在这个范围内,除了最后一组退火板变形数据略有偏离, 可能是由于表面应力水平过低导致的测试误差偏大所致.整体来看,实验结果与模型计算结果吻合性较好,偏差最大为47 μm,最小16 μm,偏差值为计算值的平均值与实验值的差值.
| 表 3 计算与实验测得的挠度对比 Table 3 Contrast of calculated and experimental deflection |
由表 3可以看出,影响模型计算的准确性主要有以下几点:1) 框架件加工中存在的薄壁壁厚误差很容易造成整体件的弯扭综合变形,易导致计算结果的偏差;2) 框架构件壁厚加工误差以及薄壁框架分割后的截面系数计算误差,也会导致模型计算的准确度;3) 模型计算的准确性与表面应力测试的准确性直接相关,而表面应力测试精度由于材料表面组织的性状特征存在着一定的不确定性,应力范围的波动也导致了计算结果的波动.同时还发现,经过退火的两构件加工后变形挠度分别为三口型40 μm与多框架型69 μm,相比于未经过退火的其他构件变形减小,可见在相同加工工艺和相同加工应力分布条件下,初始应力强度与分布对构件变形的影响极为关键.
综上,这种基于实验-解析方式构建的薄壁框架件的弯曲力学模型,以及结合表面应力测试来预测薄壁框架件铣削加工变形的方法具有可行性.该方法最大优势在于对将要加工获得的薄壁框架件,计算模型只需要获得结构尺寸、表面应力、制备方式和加工工艺即可预测构件加工后的变形情况,而这些在实践中都容易得到,避免了框架件复杂的应力场建模和弯矩积分计算.
3 结论1) 铝合金厚板初始应力场分布,与加工后的加工应力分布场是导致薄壁框架件加工后变形的主要原因,且这类框架件变形呈外凸状,这与力学模型的分析结果一致.
2) 弯曲应力形变解析模型能够描述试件应力场与构件最大变形挠度的关系,这可在铝合金构件铣削加工中起到变形预测作用,如解析模型反映了加工应力的强度及影响层深对变形的影响,铣削加工时控制加工应力的大小和深度就可以有效控制变形.
3) 变形计算模型实现了对实际结果的较好预测,这对工程应用具有较好的参考价值.
| [1] | 张烘州, 戎斌, 陈洁. 航空铝合金整体结构件数控加工变形控制现状分析[J]. 航空制造技术, 2012, 12 : 58–61. ZHANG Hongzhou, RONG Bin, CHEN Jie. Deformation control analysis of NC machining for aircraft aluminium alloy integrated component part[J]. Aviation Manufacturing Technology, 2012, 12 : 58–61. |
| [2] | 石广丰, 王景梅, 宋林森. 薄壁零件的制造工艺研究现状[J]. 长春理工大学学报, 2012, 35 (1) : 68–74. SHI Guangfeng, WANG Jingmei, SONG Linsen. Research status of manufacturing process of thin-walled workpiece[J]. Journal of Changchun University of Science and Technology, 2012, 35 (1) : 68–74. |
| [3] | 张安顺, 隋少春, 卢朝琴, 等. 超大型壁板类零件加工变形控制技术[J]. 航空制造技术, 2012, 17 : 57–59. ZHANG Aanshun, SUI Shaochun, LU Zaoqin. Giant panel part machining deformation control technology[J]. Aviation Manufacturing Technology, 2012, 17 : 57–59. |
| [4] | 成群林, 柯映林, 董辉跃. 航空整体结构件铣削加工变形预测研究[J]. 浙江大学学报, 2007, 41 (5) : 799–803. CHENG Qunlin, KE Yinglin, DONG Huiyao. Distortion prediction for milling process of aerospace monolithic components[J]. Journal of Zhejiang University, 2007, 41 (5) : 799–803. |
| [5] | 陈军, 段雨露, 彭小燕, 等. 7475-T7351铝合金厚板的疲劳性能[J]. 中国有色金属学报, 2015, 25 (4) : 890–899. CHEN J, DUAN Y L, PENG X Y, et al. Fatigue performance of 7475-T7351 aluminum alloy plate[J]. The Chinese Journal of Nonferrous Metals, 2015, 25 (4) : 890–899. |
| [6] | 张新明, 何道广, 刘胜胆, 等. 多级强化固溶处理对7050铝合金厚板强度和断裂韧性的影响[J]. 中国有色金属学报, 2012, 22 (6) : 1546–1554. ZHANG Xingming, HE Daoguang, LIU Shemhtan, et al. Effects of multi-stage promotively-solutionizing treatment on strength and fracture toughness of 7050 aluminum alloy thick plate[J]. The Chinese Journal of Nonferrous Metals, 2012, 22 (6) : 1546–1554. |
| [7] | 梅中义, 王运巧, 范玉青. 飞机结构件数控加工变形控制研究与仿真[J]. 航空学报, 2005, 26 (2) : 234–239. MEI Zhongyi, WANG Yunqiao, FAN Yuqing. Researching and simulating deformation of aerocraft structure part in NC machining[J]. Acta Aeronautica Et Astronautica Sinica, 2005, 26 (2) : 234–239. |
| [8] | 王运巧, 梅中义, 范玉青. 航空薄壁结构件数控加工变形控制研究[J]. 现代制造工程, 2005 (1) : 31–33. WANG Yunqiao, MEI Zhongyi, FAN Yuqing. Research on deformation in NC machining of aerospace thin-walled structure part[J]. Modern Manufacturing Engineering, 2005 (1) : 31–33. |
| [9] | 王运巧, 梅中义, 范玉青. 航空薄壁弧形件加工变形的非线性有限元分析[J]. 航空制造技术, 2004 (6) : 84–86. WANG Yunqiao, MEI Zhongyi, FAN Yuqing. Nonlinear finite element analysis of deformation in machining of thin-wall arc shaped workpiece[J]. Aeronautical Manufacturing Technology, 2004 (6) : 84–86. |
| [10] | 王光宇.铝合金薄壁件铣削变形仿真及疲劳寿命预测[D].长沙:中南大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10533-1011178868.htm |
| [11] | 王晓燕.铝合金薄壁件铣削变形模型及其残余应力的研究[D].长沙:中南大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014148260.htm |
| [12] | 唐志涛, 刘战强, 艾兴. 金属切削加工热弹塑性大变形有限元理论及关键技术研究[J]. 中国机械工程, 2007, 18 (6) : 746–751. TANG Zhitao, LIU Zhanqiang, AI Xing, et al. A study of thermo-elastic-plastic large-deformation finite element theory and key techniques of metal cutting simulation[J]. China Mechanical Engineering, 2007, 18 (6) : 746–751. |
| [13] | 林爱琴, 郑敏利, 樊春光, 等. 初始残余应力对铝合金7475板件变形的解析法研究[J]. 工艺与检测, 2012, 6 : 113–117. LIN Aiqin, ZHENG Minli, FAN Chunguang, et al. Analytical method research of the initial residual stress on the deformation of aluminum alloy 7475 plates[J]. Technology and Test, 2012, 6 : 113–117. |
| [14] | 成群林, 柯映林, 董辉跃. 航空铝合金高速铣削加工的有限元模拟[J]. 浙江大学学报, 2006, 40 (1) : 113–117. CHENG Qunlin, KE Yinglin, DONG Huiyao. Simulation of high-speed milling process of aerospace aluminum alloy[J]. Journal of Zhejiang University, 2006, 40 (1) : 113–117. |
| [15] | NERVI S. A mathematical model for the estimation of residual stresses in aluminum parts [D]. Washington : Washington University, 2005. |
| [16] | YOUNG K A. Machning-induced residual stress and distortion of thin parts[D]. Washington: Washington University, 2005. |
| [17] | IMED Z, VICTOR S. A force-temperature model including a constitutive law for dry high speed milling of aluminum alloys[J]. Journal of Materials Processing Technology, 2009, 209 (5) : 2532–2544. DOI: 10.1016/j.jmatprotec.2008.05.050 |
| [18] | WEINERT K, GRUNERT S, KERSTING M. Analysis of cutting technologies for lightweight frame components in flexible manufacture of lightweight frame structures[J]. Advanced Materials Research, 2006, 10 : 121–132. DOI: 10.4028/www.scientific.net/AMR.10 |
| [19] | WEINERT K, GRUNERT S, KERSTING M. Experimental and computational analysis of machining processes for light-weight aluminum structures[J]. Advanced Materials Research, 2008, 43 : 97–104. DOI: 10.4028/www.scientific.net/AMR.43 |
| [20] | ROBINSON J S, TANNER D A, TRUMAN C E, WINPORY R C. Measurement and prediction of machining of machining induced redistribution of residual stress in the aluminum alloy 7449[J]. Experimental Mechanics, 2011, 51 : 981–993. DOI: 10.1007/s11340-010-9389-4 |
| [21] | 廖凯, 刘义鹏, 常星宇. 加工应力对铝合金薄壁框架件的弯曲形变影响[J]. 轻合金加工技术, 2015, 43 (9) : 60–62. LIAO Kai, LIU Yipeng, CHANG Xingyu. Influence of machining stress on deformation of thin-walled frame components of aluminum alloy[J]. Light Alloy Fabrication Technology, 2015, 43 (9) : 60–62. |
| [22] | SCHAJERGary S, SMITH David J. Practical Residual Stress Measurement Methods. New York: John wiley Sons Lty, 2013 : 66 -87. |
| [23] | 廖凯, 吴运新, 龚海, 等. 积分法在铝合金厚板残余应力中的应用研究[J]. 中国有色金属学报, 2009, 19 (6) : 1020–1024. LIAO Kai, WU Yunxin, GONG Hai, et al. Application research of integral method to residual stress through-depth in aluminum alloy thick plate[J]. The Chinese Journal of Nonferrous Meta, 2009, 19 (6) : 1020–1024. |
 2016, Vol. 24
2016, Vol. 24


