早期缝合设备一般采用缝纫机进行双面缝制,单面缝合技术是为了解决双面缝合的局限性而研发的[1].目前德国KSL公司已经制造出了基于工业机器人和单面缝合机构的复合材料缝合系统,并应用于航空航天、汽车等行业[2-3].在国内,针对复合材料的缝合技术研究起步较晚,目前仅停留在缝合工艺参数与性能[4-7]以及单面缝合设备开发[8]的研究阶段.在缝合接缝跟踪控制的研究方面,姜海珍[9]提出了一种对于平面复合材料预制件的接缝跟踪系统,但其研究并未提到对于曲面复合材料的三维预制件的视觉接缝提取.相关文献中也并未提到复杂曲面接缝工件的路径规划方法.
本文针对曲面复合材料缝合机器人自动路径规划问题进行研究,首先采用光栅扫描仪获得预制件点云信息,通过手眼标定完成点云坐标在摄像机坐标系到机器人坐标系下的映射;然后将转化结果应用于曲面复合材料缝合路径规划中,并提出一种机器人操作空间缝合轨迹及姿态规划算法;最后对规划结果进行了机器人离线编程仿真与试验.
1 视觉接缝提取系统图 1为曲面复合材料预制件接缝自动缝合系统.系统由单边缝合设备、缝合机器人、三维光栅扫描仪及工控机组成.自主开发的单边缝合设备作为主要缝合工作装置,装载于ABB机器人末端,组成缝合动作执行机构,并通过工具标定确定机器人与缝合机构间位姿关系.机器人视觉系统采用Eye-to-hand[10-11]方案,将三维光栅扫描仪固定于机器人工作台旁,通过四点标定法确定机器人与三维光栅扫描仪之间手眼关系.缝合过程中,首先用三维光栅扫描仪对预制件整体点云数据进行采集,获得摄像机坐标系下预制件的点云坐标数据;进而根据手眼关系矩阵得到机器人坐标系下预制件的点云坐标数据;对接缝处点云数据特征进行一系列处理,提取点云边缘计算接缝中心线;通过缝合轨迹及姿态的规划算法进行机器人的路径规划;最后将规划好的操作空间路径信息通过离线编程软件传递给机器人控制柜,并控制机器人完成空间曲线接缝的缝合.

|
图 1 系统结构示意图 Figure 1 Structural diagrams of system |
三维光栅扫描仪属于双目视觉系统,为实现机器人的手眼标定需要首先进行单目相机的标定.对单目相机标定,可通过对靶标物特征点的采集并代入内外参模型公式获得单目相机的内外参数.分别标定完左右相机的内外参数之后,还需对双目系统的结构参数进行标定.本文选用横向间距21.6 mm,纵向间距19.8 mm圆形标靶,基于三维光栅扫描仪软件平台,通过对5组靶标信息的采集,完成双目相机内外参数以及结构参数的标定.标定完成后,可以通过三维光栅扫描仪获得摄像机坐标系下的预制件点云坐标数据.
2.2 手眼关系标定将预制件在机器人坐标系下的坐标数据用于机器人控制,需要将目标物在摄像机坐标系下的坐标转化到机器人坐标系下.根据Eye-to-hand视觉系统摄像机固定的特点,本文设计了一种四点标定法完成手眼关系求解.
设点空间中一点为Q,设该点在机器人坐标系下的坐标为 (xw, yw, zw),该点在摄像机坐标系下的坐标为 (xc, yc, zc), 根据坐标系齐次变换的转化方程,两个坐标系存在如下转化关系:
| $\left[ {\begin{array}{*{20}{c}} {{x_{\rm{e}}}}\\ {{y_{\rm{e}}}}\\ {{z_{\rm{e}}}}\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{T}}_{\rm{g}}}\left[ {\begin{array}{*{20}{c}} {{x_{\rm{w}}}}\\ {{y_{\rm{w}}}}\\ {{z_{\rm{w}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{n_x}} & {{o_x}} & {{a_x}} & {{t_x}}\\ {{n_y}} & {{o_y}} & {{a_y}} & {{t_y}}\\ {{n_z}} & {{o_z}} & {{a_z}} & {{t_z}}\\ 0 & 0 & 0 & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{w}}}}\\ {{y_{\rm{w}}}}\\ {{z_{\rm{w}}}}\\ 1 \end{array}} \right].$ | (1) |
该方程含有12个未知数,3个线性方程,至少需要4组点来求取转换矩阵,即:
| ${\mathit{\boldsymbol{T}}_{\rm{c}}} = {\mathit{\boldsymbol{T}}_{\rm{g}}}{\mathit{\boldsymbol{T}}_{\rm{w}}}.$ | (2) |
式中
| $\begin{array}{l} {\mathit{\boldsymbol{T}}_{\rm{c}}} = \left[ {\begin{array}{*{20}{c}} {{x_{{\rm{c1}}}}} & {{x_{{\rm{c2}}}}} & {{x_{{\rm{c3}}}}} & {{x_{{\rm{c4}}}}}\\ {{y_{{\rm{c1}}}}} & {{y_{{\rm{c2}}}}} & {{y_{{\rm{c3}}}}} & {{y_{{\rm{c4}}}}}\\ {{z_{{\rm{c1}}}}} & {{z_{{\rm{c2}}}}} & {{z_{{\rm{c3}}}}} & {{z_{{\rm{c4}}}}}\\ 1 & 1 & 1 & 1 \end{array}} \right],\\ {\mathit{\boldsymbol{T}}_{\rm{w}}} = \left[ {\begin{array}{*{20}{c}} {{x_{{\rm{w1}}}}} & {{x_{{\rm{w2}}}}} & {{x_{{\rm{w3}}}}} & {{x_{{\rm{w4}}}}}\\ {{y_{{\rm{w1}}}}} & {{y_{{\rm{w2}}}}} & {{y_{{\rm{w3}}}}} & {{y_{{\rm{w4}}}}}\\ {{z_{{\rm{w1}}}}} & {{z_{{\rm{w2}}}}} & {{z_{{\rm{w3}}}}} & {{z_{{\rm{w4}}}}}\\ 1 & 1 & 1 & 1 \end{array}} \right]. \end{array}$ |
同时,又因为
| $\left| {{\mathit{\boldsymbol{T}}_{\rm{w}}}} \right| \ne 0,$ | (3) |
进而转化式 (2) 得
| ${\mathit{\boldsymbol{T}}_{\rm{g}}} = {\mathit{\boldsymbol{T}}_{\rm{c}}}\mathit{\boldsymbol{T}}_{\rm{w}}^{ - 1}.$ | (4) |
其中,(xci, yci, zci),),(xwi, ywi, zwi) 此处 (i=1, 2, 3, 4),分别为空间内任意4点在摄像机坐标系与机器人坐标系下的坐标.这里机器人坐标系下的坐标可以通过机器人对标定杆进行示教获得;摄像机坐标系下的坐标可以通过三维光栅扫描仪获得.由式 (4) 可知,4组对应点可以求得手眼关系.为了减小误差,本文对标定杆位置进行了10次变换及采集,经组合计算得到C104=210组解,其最优解Tg应满足 (5) 所示条件.
| $\min \left\{ {\sum\limits_{i = 1}^{10} {{{\left\| {{\mathit{\boldsymbol{P}}_{{\rm{c}}i}} - {\mathit{\boldsymbol{T}}_{{\rm{g}}i}} \cdot {\mathit{\boldsymbol{P}}_{{\rm{w}}i}}} \right\|}_F}} } \right\}\left( {j = 1,2, \cdots ,210} \right).$ | (5) |
式中,Pci、Pwi分别指10组对应点中的摄像机坐标系下的坐标和机器人坐标系下的坐标,Tgj是通过式 (4) 计算所得第j组解,使式 (5) 取得最小值的第j组解即为所求矩阵.
2.3 缝合物预制件三维坐标信息三维光栅扫描仪采样得到的预制件点云数据,经过手眼关系标定,可转化为机器人坐标系下点云数据.同时,在采样过程中,根据预制件预缝合处的特征设置合适的阈值,扫描获得带有接缝特征的预制件点云数据图 2(a).进一步对三维点云进行边缘提取、去除噪声等[12-14]处理, 结果如图 2(b)所示.

|
图 2 预制件点云数据处理结果 Figure 2 Results of preform point cloud processing: (a) point cloud of preform; (b) point could of seam′s feature |
机器人进行缝合工作时需要得到执行机构的位姿信息.单边缝合设备作为缝合机器人的执行机构,其主要动作由引线机构及挑线机构实现,挑线针与引线针平行布置辅助引线针工作,缝合工作时仅需要对引线针进行路径规划.因此,本文通过对接缝中心线及缝合微切平面的拟合,完成机器人运动空间前进矢量及接近矢量[15-17]的计算,进而完成机器人的路径规划.
3.1 机器人缝合轨迹规划将得到的接缝上下边缘点云坐标,均匀采样各K个点,通过中心线公式 (6) 得到接缝中心线上的一组点云坐标.
| $\left\{ \begin{array}{l} X\left( i \right) = \frac{{{X_1}\left( i \right) + {X_2}\left( i \right)}}{2}\\ Y\left( i \right) = \frac{{{Y_1}\left( i \right) + {Y_2}\left( i \right)}}{2}\\ Z\left( i \right) = \frac{{{Z_1}\left( i \right) + {Z_2}\left( i \right)}}{2} \end{array} \right..$ | (6) |
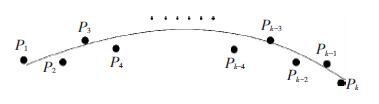
式中:X、Y、Z为中心线上路径点的坐标值,X1、Y1、Z1和X2、Y2、Z2分别为均匀离散化之后上下两条边缘点的坐标值.根据连续K个点坐标按照三次多项式进行空间曲线拟合, 进而得到接缝点的空间位置,如图 3所示
|
图 3 路径点拟合 Figure 3 Path spots fitting |
用于拟合接缝中心线路径点的函数参数形式如公式 (7) 所示
| $\left\{ \begin{align} &X={{a}_{0}}{{t}^{3}}+{{a}_{1}}{{t}^{2}}+{{a}_{2}}t+{{a}_{3}} \\ &Y=\begin{matrix} {{b}_{0}}{{t}^{3}}+{{b}_{1}}{{t}^{2}}+{{b}_{2}}t+{{b}_{3}}&t=\left( 1,2,\cdots ,K \right) \\ \end{matrix} \\ &Z={{c}_{0}}{{t}^{3}}+{{c}_{1}}{{t}^{2}}+{{c}_{2}}t+{{c}_{3}} \\ \end{align} \right.$ | (7) |
式中:a0、a1、a2、b0、b1、b2、c0、c1、c2为多项式系数; t为参数; K为离散点的个数.当赋予参数t不同值时,即可得到曲线上不同位置的点的坐标;同时,拟合所得空间曲线为一条连续平滑的曲线,对于曲线上任一点t∈[1, k]均存在不为0的x′(t)、y′(t)、z′(t),作为空间曲线的切向量,因此得到缝合头前进方向n′.
| ${{n}^{'}}={{\left( \frac{\partial X}{\partial t},\frac{\partial Y}{\partial t},\frac{\partial Z}{\partial t} \right)}^{\text{T}}}.$ | (8) |
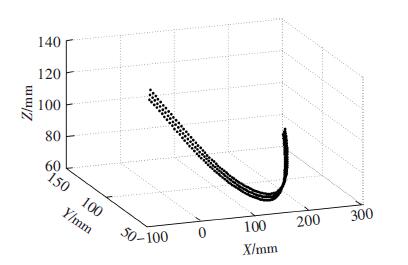
为了保证缝合工艺良好,单边缝合工作中引线针始终与预制件表面保持垂直,即保证缝针方向与缝合微切平面法矢方向保持一致.本文将微切平面法矢称为缝合机器人操作空间的接近矢量,通过对接近矢量的计算完成机器人姿态规划.采用上下接缝边缘均匀离散点以及上一步求取的中心线离散点进行法矢计算,数据点模型如图 4所示.
|
图 4 接缝边缘及中心线点云 Figure 4 Seam edge and center line point cloud |
以中心线上的采样点i及k-1个临近点Qj(j=1, 2, …, k-1) 作为局部参考,k的取值由点云密度确定.根据最小二乘法对缝合微切平面进行拟合.一般平面方程表达式为
| $F\left( x,y,z \right)=Ax+By+Cz+D=0.$ | (9) |
转化方程为
| $z=-\frac{A}{C}x-\frac{B}{C}y-\frac{D}{C}={{a}_{0}}x+{{a}_{1}}y+{{a}_{2}}.$ | (10) |
采用最小二乘法对包括该采样点在内的k个点进行微切平面拟合,拟合方程为
| $S=\sum\limits_{i=0}^{k}{{{\left( {{a}_{0}}{{x}_{i}}+{{a}_{0}}{{y}_{i}}+{{a}_{2}}-{{z}_{i}} \right)}^{2}}},$ | (11) |
即
| $\frac{\partial S}{\partial {{a}_{k}}}=0,k=0,1,2.$ | (12) |
通过计算可得:
| $\left\{ \begin{align} &\sum{2\left( {{a}_{0}}{{x}_{i}}+{{a}_{1}}{{y}_{i}}+{{a}_{2}}-{{z}_{i}} \right){{x}_{i}}}=0 \\ &\sum{2\left( {{a}_{0}}{{x}_{i}}+{{a}_{1}}{{y}_{i}}+{{a}_{2}}-{{z}_{i}} \right){{y}_{i}}}=0 \\ &\sum{2\left( {{a}_{0}}{{x}_{i}}+{{a}_{1}}{{y}_{i}}+{{a}_{2}}-{{z}_{i}} \right){{z}_{i}}}=0 \\ \end{align} \right..$ | (13) |
转化为矩阵形式:
| $\left[ \begin{matrix} \sum{x_{i}^{2}}&\sum{{{x}_{i}}{{y}_{i}}}&\sum{{{x}_{i}}} \\ \sum{{{x}_{i}}{{y}_{i}}}&\sum{y_{i}^{2}}&\sum{{{y}_{i}}} \\ \sum{{{x}_{i}}}&\sum{{{y}_{i}}}&n \\ \end{matrix} \right]\left[ \begin{matrix} {{a}_{0}} \\ {{a}_{1}} \\ {{a}_{2}} \\ \end{matrix} \right]=\left[ \begin{matrix} \sum{{{x}_{i}}{{z}_{i}}} \\ \sum{{{y}_{i}}{{z}_{i}}} \\ \sum{{{z}_{i}}} \\ \end{matrix} \right].$ | (14) |
将点云数据代入式 (14) 中,可得a0、a1、a2的值,o′=(a0 , a1, -1) 即为接近矢量的方向.
将式 (8) 所得切线方向向量n′与接近矢量方向向量o′单位化,得到单位矢量n、o,根据右手定则,矢量n和o够成右手矢量合集,由式 (15) 求得法线矢量a
| $\mathit{\boldsymbol{a}}=\mathit{\boldsymbol{n}}\times \mathit{\boldsymbol{o}}.$ | (15) |
根据上述分析,可建立接缝路径点Pi处的位姿矩阵Tp:
| ${{\mathit{\boldsymbol{T}}}_{p}}=\left[ \begin{matrix} \mathit{\boldsymbol{n}} & \mathit{\boldsymbol{o}} & \mathit{\boldsymbol{a}} & \mathit{\boldsymbol{P}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right].$ | (16) |
实验所采用预制件材料为如图 5所示厚度为5 mm的玻璃纤维,通过手眼标定得到如式 (17) 所示手眼关系矩阵
| $\left[ \begin{matrix} 0.787\,6&-0.595\,4&0.185\,6&153.143\,1 \\ -0.433\,3&-0.407\,3&0.777\,1&141.976\,0 \\ -0.375\,5&-0.729\,3&-0.607\,2&286.904\,1 \\ 0&0&0&1 \\ \end{matrix} \right].$ | (17) |

|
图 5 缝合预制件 Figure 5 Suture of preform |
采集预制件点云数据并处理,得到缝合路径中心线空间曲线方程如下:
| $\left\{ \begin{align} &X=3.177\times {{10}^{-5}}{{t}^{3}}-7.041\times {{10}^{-3}}{{t}^{2}}-0.3994t+180.8 \\ &Y=1.236\times {{10}^{-5}}{{t}^{3}}+2.448\times {{10}^{-2}}{{t}^{2}}-2.056t+128.8 \\ &Z=1.397\times {{10}^{-4}}{{t}^{3}}-1.551\times {{10}^{-2}}{{t}^{2}}-2.834t+268.4 \\ \end{align} \right..$ | (18) |
机器人缝合过程中, 不同位置的位姿可以通过对参数t进行赋值求得.本实验对曲线上20个位置的坐标进行求解,结果如表 1所示.
| 表 1 曲线离散点 Table 1 Discrete points of curve |
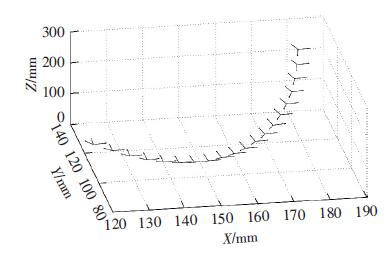
对表 1中各点进行位姿矩阵求解,序号为1的点处的位姿矩阵如式 (19) 所示,求得每一个点的前进矢量、接近矢量及法线矢量, 即可得知工具位姿,缝合路径规划坐标系仿真如图 6所示.
| $\left[ \begin{matrix} -0.1194&0.2371&-0.9641&180.3936 \\ -0.5630&0.8160&-0.1310&126.7685 \\ -0.8178&-0.5372&0.2309&265.5506 \\ 0&0&0&1 \\ \end{matrix} \right]$ | (19) |
|
图 6 路径规划坐标系仿真 Figure 6 Coordinate system simulation of path planning |
示教机器人沿接缝中心线进行运动并记录下机器人实际工作空间中的各点坐标,分析计算实际缝合工作路径点与计算所得路径点的距离偏差.
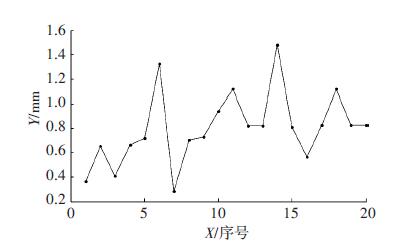
从图 7中可以看出,路径点实际坐标值与计算所得路径点坐标值总体偏差在1.5 mm以内,偏差小于1 mm的路径点达80%以上,清除特征线如图 8(b)所示,线迹成型良好,满足精度要求.
|
图 7 误差曲线 Figure 7 Error curve |

|
图 8 预制件缝合实验 Figure 8 Stitching test of preform:(a) stitching result; (b) stitching forming |
1) 为解决曲面复合材料缝合机器人自动路径规划问题,设计了基于三维光栅扫描技术的三维缝合机器人接缝视觉提取系统.
2) 对摄像机进行标定实验,改进了传统手眼标定方法,完成机器人坐标系与摄像机坐标系下点云坐标的转化.
3) 提出了一种缝合轨迹及姿态规划算法,快速地对机器人缝合过程中末端操作器的位姿进行求解,并进行了仿真与实验.
| [1] | 白榕. 碳纤维针织复合材料的开发应用[J]. 针织工业, 2015(2): 29–33. BAI Rong. A research on the development of carbon fiber knitted composite materials[J]. Knitting Industries, 2015(2): 29–33. |
| [2] | MAZARI A., HAVELKA A. Tensile properties of sewing thread and sewing needle temperature at different speed of sewing machine[J]. Advanced Materials Research, 2013, 627: 456–460. |
| [3] | WANG W, HE L, MAO W. A numerial study on the mechanical behavior of composite suture joint structure[C]//30th Annual Technical Conference of the American Society for Composites. East Lansing, MI, United states: DEStech Publications, 2015:1402-1408. |
| [4] | 顾轶卓, 李敏, 李艳霞, 等. 飞行器结构用复合材料制造技术与工艺理论进展[J]. 航空学报, 2015, 36(8): 2773–2797. GU Yizhuo, LI Min, LI Yanxia, et al. Progress on manufacturing technology and process theory of aircraft composite structure[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2773–2797. |
| [5] | 李丽英, 孟松鹤, 许承海, 等. 织物结构对复合材料力学性能影响的试验研究[J]. 材料科学与工艺, 2015, 23(1): 6–12. LI Liying, MENG Songhe, XU Chenghai, et al. Experimental study on influence of fabric structure on mechanical properties of composites[J]. Materials Science and Technology, 2015, 23(1): 6–12. |
| [6] | 刘元军, 赵晓明, 拓晓. 石墨/碳化硅/铁氧体涂层复合材料性能研究[J]. 材料科学与工艺, 2016, 24(1): 90–96. LIU Yuanjun, ZHAO Xiaoming, TUO Xiao. Study on the property of graphite/silicon carbide/ferrite composite coating materials[J]. Materials Science and Technology, 2016, 24(1): 90–96. DOI: 10.11951/j.issn.1005-0299.20160115 |
| [7] | 匡宁, 陈同海, 钱育胜. 中空复合材料的成型工艺及应用进展[J]. 工程塑料应用, 2015(1): 120–123. KUANG Ning, CHEN Tonghai, QIAN Yusheng. Progress in molding technology and application of hollow composites[J]. Engineering Plasitcs Application, 2015(1): 120–123. |
| [8] | 姚福林, 李亮玉, 岳剑锋, 等. 复合材料单边缝合机械手线迹稳定成型技术研究[J]. 机械工程学报, 2016, 52(13): 60–67. YAO Fulin, LI Liangyu, YUE Jianfeng, et al. The stitch stable forming technology of one-side sewing manipulator applied in composite material[J]. Journal of Mechanical Engineering, 2016, 52(13): 60–67. |
| [9] | 姜海珍. 三维纺织复合材料预制件缝合机器人视觉系统的研究[D]. 天津: 天津工业大学, 2008: 40-46. |
| [10] | 沈爱华, 罗印升, 宋伟. 一种基于双目视觉的手眼标定方法[J]. 机械设计与制造工程, 2016, 45(5): 42–46. SHEN Aihua, LUO Yinsheng, SONG Wei. An approach to hand-eye calibration based on stereo vision[J]. Machine Design and Manufacturing Engineering, 2016, 45(5): 42–46. |
| [11] | FREDRIK B C, ROLF J, ANDERS R. Six DOF Eye-to-hand calibration from 2D measurements using planar constraints[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany: Institute of Electrical and Electronics Engineers Inc, 2015:3628-3632. |
| [12] | WANG Y, EWERT D, SCHILBERG D, et al. Edge extraction by merging 3D point cloud and 2D image data[C]//201310th International Conference and Expo on Emerging Technologies for a Smarter World. Melville NY, United states: IEEE Computer Society, 2014:773-785. |
| [13] | CAO Jia, XU Hongli.Fast point cloud skeleton extraction via octree-graph[C]//5th International Conference on Computer Engineering and Networks, Shanghai:[s.n.], 2015: 36-41. |
| [14] | 吴禄慎. 一种基于散乱点云的边界提取算法[J]. 计算机应用与软件, 2014, 31(11): 264–268. WU Lushen. A boundary extraction algorithm based on scattered point cloud[J]. Computer Applications and Software, 2014, 31(11): 264–268. DOI: 10.3969/j.issn.1000-386x.2014.11.67 |
| [15] | WANG Xuewu, SHI Yingpan, DING Dongyan, et al. Double global optimum genetic algorithm-particle swarm optimization-based welding robot path planning[J]. Engineering Optimization, 2016, 48(2): 299–316. DOI: 10.1080/0305215X.2015.1005084 |
| [16] | LV Hongwei. Study on welding path planning of welding position flock for welding robot based on improved genetic algorithm[J]. Applied Mechanics and Materials, 2014, 602-605: 1332–1335. DOI: 10.4028/www.scientific.net/AMM.602-605 |
| [17] | 秦涛. 基于结构光视觉传感器的焊缝实时跟踪控制[D]. 上海: 上海交通大学, 2012: 49-55. |
 2017, Vol. 25
2017, Vol. 25


