医疗、通讯和航空航天领域的持续微型化趋势对微型零件的制造提出了更高的工艺需求.金属微成形工艺以其高产量、低能耗的优势而得到广泛关注.然而,尺寸效应的出现使得成熟的宏观金属成形理论不能以相似缩放的方法应用到微成形工艺的指导中, 需要对金属的微成形机理进行重新研究[1-5].
Geiger等通过圆柱微墩粗发现,流动应力值随试样几何尺寸的减小而减小,并据此提出了著名的微成形表面层模型[6].Fu教授等对不同晶粒尺寸的圆柱试样进行墩粗,发现流动应力随晶粒尺寸的增大而减小,并由此建立了描述微成形材料行为的本构方程[7].在薄板 (0.01 mm≤t≤1 mm) 成形方面,Kals等通过对不同厚度的CuNi18Zn20薄板进行拉伸,发现薄板厚度尺寸对流动应力的影响规律与微墩粗圆柱的直径影响相似[3].Peng等认为微成形材料的变形行为居于多晶和单晶之间[8].此外,Muammer等通过对304不锈钢薄板进行胀形试验发现,晶粒尺寸的变化对薄板力学性能的影响要强于进行拉伸,发现薄板厚度尺寸对流动应力的影响规律与微墩粗圆柱的直径影响相似[3].Peng等认为微成形材料的变形行为居于多宏观板材[9].
上述研究表明,微成形材料的力学性能同时受到试样尺寸和晶粒尺寸的影响.然而,当试样几何尺寸持续减小到与晶粒尺寸同一数量级时,个体晶粒对试样的变形行为产生显著影响.由于个体晶粒属性存在随机性,材料的各向同性假设不再成立.因此,本研究主要结合试样内个体晶粒的变形行为对材料的微成形行为及其波动现象进行研究.通过对厚度为0.4,0.1,0.05和0.03 mm的H80薄板试样进行拉伸试验,研究薄板成形中材料的强度指标和塑性指标的尺寸效应现象.
1 实验本研究所用材料为H80薄板,厚度分别为0.4,0.1,0.05和0.03 mm,轧制态.为了去除轧制硬化和获取相似的晶粒尺寸,对不同厚度的H80薄板在真空炉中以不同的温度和时间组合进行再结晶退火.采用截线法量取各试样的晶粒尺寸,对于晶粒尺寸大于厚度尺寸的试样,在厚度方向和薄板的上 (下) 表面均作晶粒尺寸测量,取平均值.最后从中选取晶粒尺寸约为34 μm的各厚度薄板作为试样.相应的材料退火参数如表 1所示.
| 表 1 退火参数 Table 1 Heat treatment parameters |
根据国标 (GB/T228.1-2010) 取拉伸试样的标距长度 (L, mm) 为50 mm,宽度 (W, mm) 为12.5 mm.在电子万能试验机上,以应变率为0.001 s-1进行单轴拉伸试验.由于H80薄板拉伸应力应变曲线没有明显屈服平台,取塑性应变为0.2%时的应力为屈服强度 (强度指标).测量试样断裂后标距长度计算断后延伸率 (塑性指标).每组测试6件,取平均值.
为了研究单个晶粒的变形行为,对变形后的拉伸试样进行显微维氏硬度测试.测试截面垂直于拉伸轴,10 g载荷下保压10 s.为避免晶界杂质等对硬度值的影响,测试前对试样进行镶嵌、抛光和腐蚀,压痕每次要确保压在晶内,如图 1所示.

|
图 1 晶内显微硬度测试图 Figure 1 The micro-hardness measuring position |
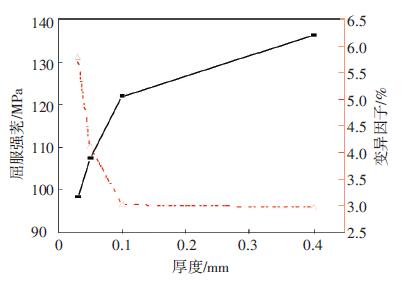
图 2显示屈服强度值随厚度值的减小而减小,表现出越小越弱的尺寸效应现象.但屈服强度值在各厚度区间的变化趋势不同.随厚度值的减小,屈服强度值在0.4~0.1 mm区间内降幅较小,而在0.1~0.03 mm区间内降幅增大.
|
图 2 厚度尺寸对强度指标的影响 Figure 2 Effects of the thickness on the strength |
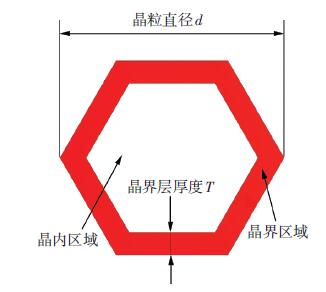
如图 3所示,晶粒由晶内区域和晶界区域组成.晶界区域由于原子排列杂乱,应变硬化率高,流动应力大.假设晶粒直径为d,晶界区域厚度与晶粒直径尺寸参考文献[10],则有
| $T = 0.133{d^{0.7}}.$ | (1) |
|
图 3 晶粒示意图 Figure 3 Grain schematic illustration |
式中T为晶界层厚度.
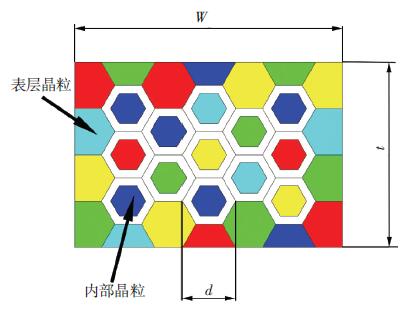
但本实验中所有试样的晶粒尺寸约为34 μm,因此,晶粒尺寸的变化不是引起上述变化的主要原因.Miyazaki等通过试验发现,仅能在试样的表层晶粒的三叉点处观察到少量位错,其他区域几乎观察不到位错[11].此外,Peng等认为,试样的表层晶粒由于存在自由表面,不受晶界的约束,其力学行为可以看做为单晶晶粒[12].如图 4所示,晶界区域在整个试样中所占的面积分数可以表示为
| $\eta = \frac{{\left( {W - 2d} \right)\left( {t - 2d} \right)\left[ {1 - {{\left( {\frac{{d - 2T}}{d}} \right)}^2}} \right]}}{{Wt}}.$ | (2) |
|
图 4 薄板试样晶粒配置示意图 Figure 4 Schematic of grain allocation in thin sheet specimens |
式中:W为试样宽度;d为晶粒直径;t为试样厚度;T为晶界层厚度.
由于试样宽度12.5 mm远大于晶粒尺寸,因此,式 (2) 可简化为
| $\eta = \frac{{\left( {t - 2d} \right)\left( {t - 2d} \right)\left[ {1 - {{\left( {\frac{{d - 2T}}{d}} \right)}^2}} \right]}}{t}.$ | (3) |
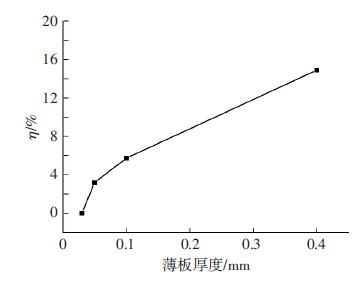
η值随厚度值的变化如图 5所示,可以看到,随试样厚度尺寸的减小,晶界区域在试样中所占的百分比减小.因此,屈服强度随试样尺寸的减小是由晶界区域所占百分比的减小引起的.
|
图 5 晶界区域百分比随厚度的变化曲线 Figure 5 Variation of grain boundary percentage with thickness |
为了研究厚度尺寸对材料屈服强度离散程度的影响,引入数理统计量变异因子C.V (Coefficient of Variation) [13-14],
| ${\rm{C}}.{\rm{V = }}\frac{S}{{\bar X}}.$ | (4) |
式中:X为均值; S为标准差.图 2显示屈服强度的变异因子值与屈服强度值呈现相反的变化趋势.变异因子值随厚度尺寸的减小而增大,且在0.1~0.03 mm区间内,变异因子迅速增大.
薄板的宏观拉伸性能是由试样内的晶粒决定的.如表 1所示,t/d值 (厚度范围晶粒数量) 随厚度的减小而减小.当厚度减小到0.03 mm时,厚度范围内仅有1个晶粒.单个晶粒在试样内所占的百分比显著增加,单个晶粒的变形行为对薄板的拉伸性能会产生显著影响.如图 6所示,6个晶粒在尺寸、取向、形状上各不相同.每个晶粒都会决定整个薄板的拉伸性能,因此,材料属性会有突然的变化,材料的变异因子值增大.

|
图 6 厚度0.03 mm H80薄板金相组织图 Figure 6 Microstructure of 0.03 mm thick H80 thin sheets |
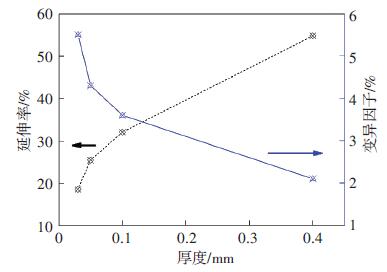
如图 7所示,薄板厚度对塑性指标的影响和强度指标类似.断裂延伸率随厚度的减小而减小,且厚度小于0.1 mm时,降幅增大.断裂延伸率的变异因子值 (断裂延伸率标准差和平均断裂延伸率之比) 也同样随厚度的减小而增大.这表明,随着薄板厚度的减小,材料的塑性性能表现极不稳定.
|
图 7 薄板厚度对塑性指标的影响 Figure 7 Effects of thickness on plasticity |
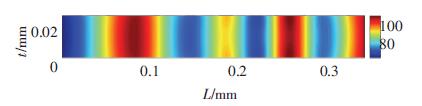
材料的应变硬化行为可以通过硬度测试来评定.沿拉伸试样横截面的宽度方向 (横向) 随机取10组晶粒进行硬度值统计分析.利用MATLAB拟合出厚度为0.03和0.4 mm H80薄板晶粒的维氏硬度值 (HV) 分布云图,如图 8和图 9所示.其中,0.03 mm厚度方向有一个晶粒,0.4 mm厚度方向有10个晶粒.由于0.03 mm薄板只有一行硬度值,拟合时假定厚度方向硬度值相同.表 2为0.03 mm厚薄板晶粒的维氏硬度值、横向均值和变异因子,表 3为0.4 mm厚薄板厚度方向的所有晶粒的平均维氏硬度值、横向均值和变异因子.
|
图 8 厚度0.03 mm H80薄板晶粒硬度云图 Figure 8 Hardness nephogram of 0.03 mm thick H80 thin sheets |
|
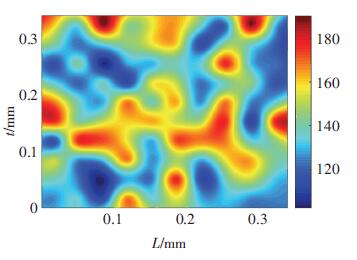
图 9 厚度0.4 mm H80薄板晶粒硬度云图 Figure 9 Hardness nephogram of 0.4 mm thick H80 thin sheets |
| 表 2 0.03 mm薄板晶粒硬度值统计分析 Table 2 Statistical analysis of hardness values for 0.03 mm thin sheets |
| 表 3 0.4 mm薄板晶粒厚向硬度均值统计分析 Table 3 Statistical analysis of mean hardness values along the thickness direction for 0.4 mm thin sheets |
如图 8和图 9所示,厚度为0.03和0.4 mm试样内的晶粒硬度值分布均离散,证明试样中各晶粒的变形情况都是不均匀的.如表 2、表 3横向硬度统计值所示,横向均值随厚度增大而增大,而横向硬度值的变异因子 (硬度标准差和硬度横向均值之比) 却随厚度值的增大而减小.这表明厚度为0.4 mm的薄板,虽然沿厚度方向各晶粒的硬度值不同,但它们沿厚度方向的均值基本是恒定的.
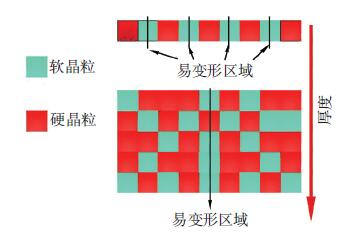
试样加载后,由于晶体取向的不同,软取向晶粒容易变形,硬取向晶粒变形困难.SACHS理论认为,当试样外加应力为σ时,试样内的每一个晶粒承受的应力也为σ[15].基于试样沿着最小功消耗的路径变形的假设,软晶粒容易变形且消耗较小的塑性功[2].对于由晶粒组成的试样,最小的塑性功消耗可以通过晶粒的弱弱组合来完成.一旦这种晶粒的弱弱组合形成,大量的塑性功将集中在此组合区域.使得该区域最早达到断裂强度,发生过早断裂.如图 10所示,试样厚度范围内的晶粒数量越少,越容易形成这种弱弱组合,因此,越容易断裂.如表 2所示,厚度尺寸只有一个晶粒,且沿横向硬度差距大,变形容易集中于某一弱取向晶粒,这最终导致厚度薄的试样的过早断裂.对于厚度大的试样来说,如表 3所示,各厚度方向的硬度均值基本相同,因此,这种弱弱组合很难形成.断裂前所有晶粒均有机会参与变形,因此,厚度尺寸大的试样的延伸率大,平均硬度值大.
|
图 10 易变形晶粒组合示意图 Figure 10 Schematic illustration of easy deformation zone |
晶粒弱弱组合的形成具有随机性.厚度尺寸越小,越容易形成这种弱弱组合,变形越容易集中在某一个特殊晶粒上.个体晶粒的随机性决定了试样断裂延伸率的波动性.而厚度尺寸大的试样,厚向弱弱组合形成困难.所有的晶粒均匀变形硬化,因此,断裂延伸率较大且个体晶粒影响较小.这正是图 7中所述厚度尺寸大的试样延伸率变异因子值小的原因.
3 结论1) 屈服强度随厚度尺寸的减小而减小.晶界区域在试样中所占百分比的减小是发生越小越弱现象的主要原因.
2) 厚度尺寸越小越容易形成晶粒间的弱弱结合.易变形区域的形成导致拉伸试样的过早断裂.
3) 屈服强度和断裂延伸率的波动性随厚度尺寸的减小而增大.个体晶粒在试样中所占百分比的增加是主要原因.
| [1] | ENGEL U, ECKSTEIN R. Microforming-from basic research to its realization[J]. J Mater Process Technol, 2002, 125(2): 35–44. |
| [2] | FU M W, CHAN W L. Micro-scaled Products Development Via Microforming[M]. Berlin: Springer Berlin, 2014 : 41-46. |
| [3] | KALS T A, ECKSTEIN R. Miniaturization in sheet metal working[J]. J Mater Process Technol, 2000, 103(1): 95–101. DOI: 10.1016/S0924-0136(00)00391-5 |
| [4] | MA Z W, TONG G Q, CHEN F, et al. Grain size effect on springback behavior in bending of Ti-2.5Al-1.5Mn foils[J]. Journal of Materials Processing Technology, 2015, 224: 11–17. DOI: 10.1016/j.jmatprotec.2015.04.025 |
| [5] | VOLLERTSEN F. Micro Metal Forming[M]. Heidelberg: Springer Berlin, 2013 . |
| [6] | GEIGER M, MESSNER A, ENGEL U. Production of microparts-size effects in bulk metal forming, similarity theory[J]. Production Engineering, 1997, 4(1): 55–58. |
| [7] | CHAN W L, FU M W, LU J, et al. Modeling of grain size effect on micro deformation behavior in micro-forming of pure copper[J]. Mater Sci Eng: A, 2010, 527(24): 6638–6648. |
| [8] | LAI X, PENG L, HU P, et al. Material behavior modelling in micro/meso-scale forming process with considering size/scale effects[J]. Computational Materials Science, 2008, 43(4): 1003–1009. DOI: 10.1016/j.commatsci.2008.02.017 |
| [9] | MAHABUNPHACHAI S, KOC M. Investigation of size effects on material behavior of thin sheet metals using hydraulic bulge testing at micro/meso-scales[J]. Int J Mach Tool Manu, 2008, 48(9): 1014–1029. DOI: 10.1016/j.ijmachtools.2008.01.006 |
| [10] | FU H-H, BENSON D J, MEYERS M A. Analytical and computational description of effect of grain size on yield stress of metals[J]. Acta Mater, 2001, 49(13): 2567–2582. DOI: 10.1016/S1359-6454(01)00062-3 |
| [11] | MIYAZAKI S, FUJITA H, HIRAOKA H. Effect of specimen size on the flow stress of rod specimens of polycrystalline Cu Al alloy[J]. Scripta Mater, 1979, 13: 447–449. DOI: 10.1016/0036-9748(79)90067-X |
| [12] | PENG L, LIU F, NI J, et al. Size effects in thin sheet metal forming and its elastic-plastic constitutive model[J]. Mater Des, 2007, 28(5): 1731–1736. DOI: 10.1016/j.matdes.2006.02.011 |
| [13] | DIEH A, ENGEL U, GEIGER M. Influence of microstructure on the mechanical properties and the forming behavior of very thin metal foils[J]. Int J Adv Manuf Technol, 2010, 47: 53–61. DOI: 10.1007/s00170-008-1851-4 |
| [14] | EICHENHUELLER Bernd, EGERER Emil, ENGEL Ulf. Microforming at elevated temperature-formingand material behaviour[J]. Int J Adv Manuf Technol, 2007, 33: 119–124. DOI: 10.1007/s00170-006-0731-z |
| [15] | SACHS G. Zur Ableitung einer fliessbedingung[J]. Z Ver Dtsch Ing, 1928, 72: 734–736. |
 2017, Vol. 25
2017, Vol. 25


