随着能源紧张和环境问题越来越突出,轻质、环保、绿色无污染成为材料研究的重要方向.镁合金是目前应用的金属结构材料中最轻的一类,因其具有较小的密度、较高的比强度和比刚度、优异的减震性能、散热性能和循环再利用性能等优点成为各国科学家研究的重点,被誉为“21世纪绿色工程材料”[1-2].稳态准晶材料具有高强度、高硬度等优异的力学性能,因此将准晶增强相引入到镁合金中,提高镁合金的力学性能,为新型镁合金的开发和实际应用提供了一种新途径.
目前,准晶材料主要作为表面改性材料或者将准晶相作为增强相弥散分布于结构材料中.张鉴等[3]研究了不同准晶含量的Mg-Zn-Gd-Y合金的高温热压缩变形行为,结果发现准晶不仅可以促进合金的动态再结晶以及孪晶的出现,而且其含量越高,合金的高温塑性变形能力越强.Xia等[4]研究了挤压Mg-Zn-Y-Zr合金在250~450 ℃、0.001~1 s-1条件下的高温压缩变形行为,确认了其在该条件下的最佳变形参数,并在该条件下进行了等温锻造测试,发现零件在时效处理后的抗拉强度达到396 MPa,屈服强度达到356 MPa,这表现出富含准晶镁合金优异的高温力学性能.
Mg-Zn-RE (Zr) 合金系中的Mg3Zn6RE准晶既可以通过快速凝固等非平衡工艺生成,也可以在常规铸造的缓慢凝固过程中生成.这种较低的生成条件为工业化生产提供了可能,现在我国已经开发出准晶增强的高强Mg-Zn-Zr-RE系合金[5].基于对该系合金基本性能的研究,为排除Zr元素的影响,本文以挤压Mg-4.5Zn-0.75Y合金为研究对象,利用Gleeble-3500热/力模拟机对其高温流动特性进行研究,同时,利用建立的Mg-4.5Zn-0.75Y合金的DMM (Dynamic Material Modeling) 加工图分析其变形及失稳机制,并结合不同加工工艺参数下合金的显微组织,确定较优的变形参数,为该合金的进一步研究奠定基础.
1 实验将Φ10 mm×15 mm的挤压Mg-4.5Zn-0.75Y合金圆柱试样在Gleeble-3500热/力模拟实验机上进行轴对称压缩试验,应变速率为0.01、0.1、1 s-1,温度设定为300、350、400 ℃.以3 ℃/s的加热速率将试样加热至预设温度,保温3 min以消除试样内部的温度差,随后开始等温压缩试验,然后立即水淬.
将压缩后的试样沿压缩方向切开,随后依次进行砂纸打磨、抛光及腐蚀处理 (腐蚀剂:草酸+硝酸+乙酸溶液,腐蚀时间15 s),最后在Zeiss Lab. A1蔡司光学显微镜下进行显微组织观察和拍照,并采用XRD技术测定材料的物相组成.
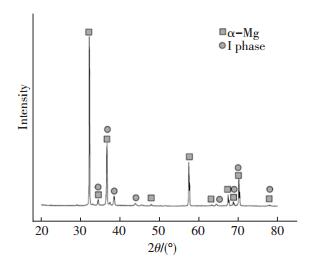
2 结果与讨论 2.1 挤压Mg-4.5Zn-0.75Y合金的显微组织图 1为挤压Mg-4.5Zn-0.75Y合金的XRD谱图,可以看出,合金物相由α-Mg基体和二十面体准晶I-Phase组成.
|
图 1 挤压Mg-4.5Zn-0.75Y合金XRD谱图 Figure 1 XRD pattern of the extruded Mg-4.5Zn-0.75Y alloy |
图 2为挤压Mg-4.5Zn-0.75Y合金的显微组织照片,可以看出:挤压Mg-4.5Zn-0.75Y合金中α-Mg基体晶粒大小不均,第二相析出并且不均匀地分布在基体中;沿挤压方向,可以发现数条挤压条带,但晶粒并没有被拉长的趋势.

|
图 2 挤压Mg-4.5Zn-0.75Y合金初始显微组织 Figure 2 Microstructures of as-extruded Mg-4.5Zn-0.75Y alloy: (a) transverse direction; (b) extrusion direction |
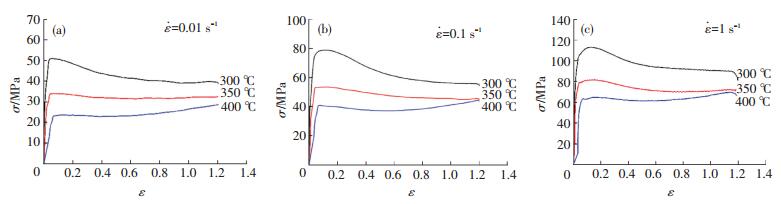
图 3为不同应变速率下Mg-4.5Zn-0.75Y合金的真应力-真应变曲线,图 4为与之对应的不同变形条件下Mg-4.5Zn-0.75Y合金沿压缩方向的显微组织照片.由图 3可知,Mg-4.5Zn-0.75Y合金高温塑性变形时,其流变应力均随着热变形温度的降低和应变速率的升高而增加,说明该合金是正应变速率敏感材料.

|
图 4 挤压Mg-4.5Zn-0.75Y合金在不同变形条件下沿压缩方向的显微组织 Figure 4 Microstructures along extrusion direction of the extruded Mg-4.5Zn-0.75Y alloy at different hot compression deformation parameters:(a) 300 ℃/0.01 s-1; (b) 300 ℃/0.1 s-1; (c) 300 ℃/ 1 s-1; (d) 350 ℃/0.01 s-1; (e) 350 ℃/0.1 s-1; (f) 350 ℃/1 s-1; (g) 400 ℃/0.01 s-1; (h) 400 ℃/0.1 s-1; (i) 400 ℃/1 s-1 |
|
图 3 不同应变速率下Mg-4.5Zn-0.75Y合金的真应力-真应变曲线
Figure 3 True stress-true strain curves of Mg-4.5Zn-0.75Y alloy at different conditions:(a) |
与图 2(b)对比可以发现,图 4显示的组织中均不存在挤压条带,仔细对比压缩前后的晶粒可以发现,在θ=300~350 ℃、
由图 3还可以看出,当温度一定时,峰值应力随应变速率的增加而升高 (如θ=300 ℃时,当应变速率从0.01 s-1上升至1 s-1时,峰值应力由51 MPa上升至131 MPa).此外,过多的位错在高应变速率下来不及抵消和合并,使得再结晶形核位置增多,导致晶粒细化,如图 4所示.随着变形的进一步进行,流变应力达到一峰值,此时加工硬化与动态再结晶造成的软化达到动态平衡.随后,流变应力的变化可以分为两类: 1) 温度较低时,随着真应变的继续增加,流变应力缓慢下降至一稳定值 (例如图 3(c),当θ=300 ℃时,流变应力由峰值113 MPa下降至90 MPa);2) 在温度较高时,真应力在上升到峰值后,基本保持不变 (例如图 3(c),当θ=400 ℃时,流变应力保持为峰值的65 MPa).
上述情况的出现是因为变形温度是影响镁合金动态再结晶的主要因素之一.温度较低时,随着真应变的继续增加,加工硬化逐渐被动态再结晶的软化作用抵消,流变应力逐渐下降并最终保持不变;当温度升高时,晶界扩散和晶界迁移能力增强,促使变形中的位错重新调整,有利于异号位错的合并和位错密度的降低,从而促进了动态再结晶的进行以及再结晶晶粒的长大[6](例如
研究发现[7-8],Mg-Zn-RE合金中生成的准晶相与基体存在半共格关系,而且在塑性变形过程中该位相关系保持不变,这种良好的匹配关系使合金在变形时不会在界面处产生微裂纹而导致材料破裂,从而使合金表现出很好的变形能力.图 5为Mg-4.5Zn-0.75Y合金在300 ℃、应变速率1 s-1时的扫描照片.由图 5(a)可以看出,该合金在应变达到1.2时,仍然没有微裂纹与空洞的产生,表现出该合金优异的变形能力.

|
图 5 挤压Mg-4.5Zn-0.75Y合金在300 ℃,应变速率为1 s-1压缩后的扫描照片 Figure 5 Typical microstructures of the Mg-4.5Zn-0.75Y alloy deformed at 300 ℃/1 s-1: (a) lower and (b) higher magnifications |
镁合金由于较低的层错能而在热变形过程中容易发生动态再结晶,准晶相的存在则会促进动态再结晶的进行.一方面,准晶相高温稳定性较好,由图 5(b)可以看出,高温压缩后准晶颗粒并没有长大,因此可为动态再结晶提供更多的形核粒子;另一方面,相比于W (Mg3Zn3Y2) 相,连贯的准晶相粒子可以提供更大的钉扎力,从而促进动态再结晶的进行.因此,准晶的存在可以提高镁合金的塑性变形能力,而且Kwak等[9]和张鉴等[3]的研究都表明,高准晶含量的合金能够表现出更好的高温塑性变形能力.
2.4 挤压态Mg-4.5Zn-0.75Y合金的本构方程对于镁合金的高温压缩试验,大部分研究人员采用Zener-Hollomon模型[10]来描述镁合金热变形过程中稳态流变应力与变形温度和应变速率之间的关系,即:
当应力水平较低时 (ασ < 0.8),用幂指数模型描为
| $ \dot \varepsilon = {A_1}{\sigma ^{n'}}\exp \left( {-Q/RT} \right); $ | (1) |
当应力水平较高时 (ασ>1.2),用指数模型描述为
| $ \dot \varepsilon = {A_2}\exp \left( {\beta \sigma } \right)\exp \left( {-Q/RT} \right). $ | (2) |
而以上两种模型在应用上都具有一定的局限性.Sellars和Tegar根据材料热变形过程和蠕变过程的相似性,用包含热变形激活能Q的Arrhenius关系来描述材料热变形过程中稳态流变应力与变形温度和应变速率之间的关系,即为广泛应用的双曲正弦模型[11]:
| $ \dot \varepsilon = A{\left[{\sinh \left( {\alpha \sigma } \right)} \right]^n}\exp \left( { -Q/RT} \right). $ | (3) |
式中:A1、A2、β均为常数;A为结构因子,s-1;n为应力指数;n′是与材料有关的常数;α为应力水平参数 (mm2/N),α=β/n′;Q为镁的变形激活能 (kJ/mol),它反映材料热变形的难易程度;R为气体常数,8.314 J/mol;T为热力学常数,K.
表 1为Mg-4.5Zn-0.75Y合金在不同变形条件下对应的峰值应力和峰值应变,对式 (1) 和 (2) 两边分别取对数,并假定变形激活能与变形温度无关,式中除了
| $ \ln \left( {\dot \varepsilon } \right) = \ln \left( {{A_1}} \right)\; + \;n'\ln \sigma, $ | (4) |
| $ \ln \left( {\dot \varepsilon } \right) = \ln \left( {{A_2}} \right)\; + \;\beta \sigma . $ | (5) |
| 表 1 Mg-4.5Zn-0.75Y合金在不同变形条件下对应的峰值应力和峰值应变 Table 1 Peak flow stresses of Mg-4.5Zn-0.75Y alloy at different temperatures and strain rates |
根据表 1中的数据,分别作出ln (
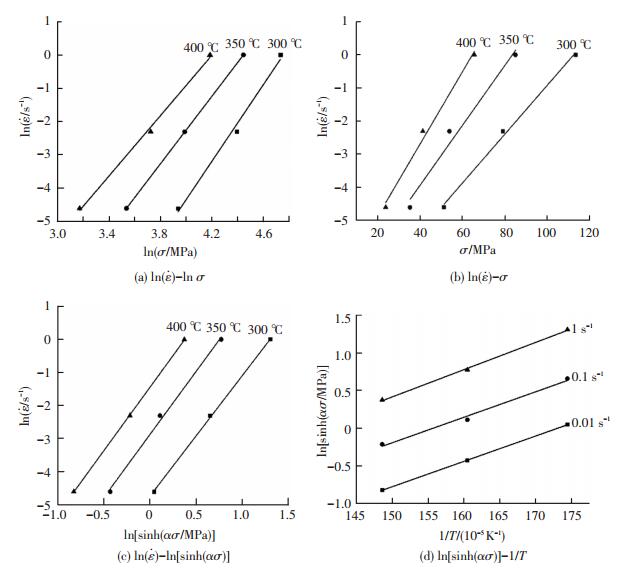
|
图 6 线性关系拟合图 Figure 6 Linear relationship fitting |
仍然假定变形激活能与变形温度无关,对式 (3) 两边取对数得
| $ \ln \left( {\dot \varepsilon } \right) = \ln \left( A \right)- Q/RT + n\ln \left[{\sinh \left( {\alpha \sigma } \right)} \right]. $ | (6) |
两边进行对数线性化处理,得到激活能的计算公式[13]
| $ Q = R \cdot {\left[{\frac{{\partial \ln \left[{\sinh \left( {\alpha \sigma } \right)} \right]}}{{\partial \left( {1/T} \right)}}} \right]_{\dot \varepsilon }}{\left[{\frac{{\partial \ln \left( {\dot \varepsilon } \right)}}{{\partial \ln \left[{\sinh \left( {\alpha \sigma } \right)} \right]}}} \right]_T}. $ | (7) |
式中:
利用最小二乘法线性回归到相应的曲线,求得n1=3.763 2和k=3 450.403 4.故Q=Rn1k=8.314 ×3.763 2 × 3.450 4 kJ/mol = 107.95 kJ/mol.
根据Zener-Hollomon模型中Z参数和流变应力关系
| $ Z = \dot \varepsilon \exp \left( {Q/RT} \right) = A{\left[{\sinh \left( {\alpha \sigma } \right)} \right]^n}. $ | (8) |
对式 (8) 两边取对数,得
| $ \ln Z = \ln A + n\ln \left[{\sinh \left( {\alpha \sigma } \right)} \right]. $ | (9) |
将表 1中的数据代入式 (8) 和 (9),并将图中的点进行线性回归,得到lnZ和ln[sinh (ασ)]点状图,如图 7所示.直线的相关系数为0.997,n值即为斜线的斜率,n=3.996 6.从图 7还可以得出直线的截距为19.240,即ln A=19.240,因此A= 2.269×108.
将计算出的相关数据代入式 (3),得到Mg-4.5Zn-0.75Y合金实验条件下的本构方程
| $ \dot \varepsilon = 2.269 \times {10^8}{\left[{\sinh \left( {0.017\;3\sigma } \right)} \right]^{3.9966}}\exp \left( { -\frac{{107.95}}{{RT}}} \right). $ | (10) |
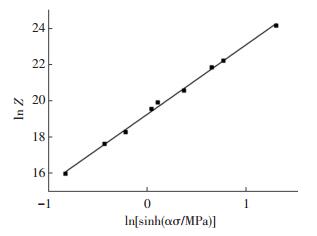
|
图 7 ln Z和ln[sinh (ασ)]的线性拟合图 Figure 7 Linear relationship fitting of ln Z and ln[sinh (ασ)] |
本文采用基于动态材料模型DMM的加工图[14-16],并依据加工图判断材料变形过程中的流变失稳区,建立材料变形温度和应变速率最佳匹配的工艺参数.
根据耗散结构理论,输入系统的能量 (P) 由两部分组成:耗散量 (G) 和耗散协量 (J),其中,G是材料发生塑性变形所消耗的能量,其大部分能量转化成了热能,小部分以晶体缺陷能的形式存储;J是材料变形过程中组织演化所耗的能量.这三者的关系为
| $ P = \sigma \dot \varepsilon = G + J = \int_0^{\dot \varepsilon } {\sigma \alpha \dot \varepsilon } + \int_0^\sigma {\dot \varepsilon } . $ | (11) |
假设材料符合本构关系
| $ \sigma = k{{\dot \varepsilon }^m}, $ | (12) |
那么耗散协量J则表示为
| $ J = \int_0^{\dot \varepsilon } {\sigma \alpha \dot \varepsilon = \frac{m}{{m + 1}}} \sigma \dot \varepsilon . $ | (13) |
式中:k为材料常数;m为材料在一定应力下的应变速率敏感指数,为G和J两种能量所占的比例,即
| $ m = \frac{{\partial J}}{{\partial G}} = \frac{{\dot \varepsilon \partial \sigma }}{{\sigma \partial \dot \varepsilon }} = \frac{{\partial \left( {\ln \sigma } \right)}}{{\partial \left( {\ln \dot \varepsilon } \right)}}. $ | (14) |
一般情况下,m值随温度和应变速率呈非线性变化.当m=1时,材料处于理想线性耗散状态,耗散协量J达到最大值Jmax:
| $ {J_{\max }} = \frac{{\sigma \dot \varepsilon }}{2}. $ | (15) |
由式 (13) 和 (15) 可以得到一个无量纲的参数η,称为耗散效率因子,其物理意义是材料成形过程中显微组织演变所耗散的能量同线性耗散能量的比例关系,其表达式为
| $ \eta = \frac{J}{{{J_{\max }}}} = \frac{{2m}}{{m + 1}}. $ | (16) |
根据计算出的η值在变形温度 (T) 和应变速率 (

|
图 8 Mg-4.5Zn-0.75Y合金在不同应变下对应的功率耗散图 Figure 8 Power dissipation map of the extruded Mg-4.5Zn-0.75Y alloy at different strain: (a) ε=0.3; (b) ε=0.6; (c) ε=0.9; (d) ε=1.2 |
根据不可逆热力学原理,可以用一个无量纲参数ξ(
| $ \xi \left( {\dot \varepsilon } \right) = \frac{{\partial \ln (m/(m + 1))}}{{\partial \ln \dot \varepsilon }} + m < 0. $ | (17) |
将功率耗散图和失稳图叠加在一起,就构成了不同真应变 (ε) 对应的DMM加工图.
图 8为Mg-4.5Zn-0.75Y合金在不同应变下对应的功率耗散图,图 8(a)、8(b)、8(c) 和8(d) 对应的应变分别为0.3、0.6、0.9和1.2.此处,功率耗散系数代表着合金在高温压缩过程中发生动态再结晶的程度,其值越大,表示在该条件下合金发生动态再结晶的程度越高.对比图 8(a)、8(b)、8(c) 和8(d)可以发现,在试样整个变形过程中,功率耗散系数逐渐降低,大致可分为3个阶段[17]:(1) 应变0~0.3这一过程,参照图 3真实应力-真实应变曲线可以发现,峰值应力都处在这一区域.这一过程发生的主要是基面滑移,晶内出现位错塞积,位错之间的相互作用形成胞状亚结构.一方面,位错的出现导致加工硬化,使合金的流变应力不断增大直至峰值;另一方面,胞状亚结构的形成为动态再结晶的发生累积了足够能量,因此,这一过程的功率耗散系数普遍偏高,最大值达到0.36.(2) 应变0.3~0.9这一阶段,胞状亚结构发生动态回复形成亚晶,亚晶界进一步迁移和合并形成大角度新晶粒,动态再结晶过程基本完成.由于此阶段动态再结晶的软化大于加工硬化,在真实应力-真实应变曲线上表现为流变应力不断下降,并逐渐趋于稳定.这一过程存在2个功率耗散系数较大的区域,分别为θ=300~320 ℃、
以式 (17) 为失稳判据,并没有得到Mg-4.5Zn-0.75Y合金在该变形条件下的失稳图,这说明该合金在此条件下具有良好的塑性.结合Mg-4.5Zn-0.75Y合金压缩后的显微组织图 (如图 4所示),综合考虑功率耗散系数与组织均匀性及晶粒大小,Mg-4.5Zn-0.75Y合金的较优热加工工艺参数为θ=300~350 ℃、
1) Mg-4.5Zn-0.75Y合金在本实验条件下的高温变形本构方程为
| $ \dot \varepsilon = 2.269 \times {10^8}{\left[{\sinh (0.017\;3\sigma )} \right]^{3.9966}}\exp \left( { -\frac{{107.95}}{{RT}}} \right). $ |
2) 挤压Mg-4.5Zn-0.75Y合金在温度300~400 ℃,应变速率0.01~1 s-1的条件下并没有发生失稳,这说明该合金在此实验条件下塑性性能良好,满足加工要求.
3) 结合Mg-4.5Zn-0.75Y合金的加工图与挤压后的显微组织图,获得该合金热加工的较优工艺参数为θ=300~350 ℃、
| [1] | 赵铎, 董刚, 赵博. 镁合金在航空领域应用的研究进展[J]. 有色金属工程, 2015, 5(2): 23–27. ZHAO Duo, DONG Gang, ZHAO Bo. Research progress of magnesium alloy application in aviation manufacturing[J]. Nonferrous Metals Engineering, 2015, 5(2): 23–27. |
| [2] | 范子杰, 桂良进, 苏瑞意. 汽车轻量化技术的研究与进[J]. 汽车安全与节能学报, 2014, 5(1): 1–16. FAN Zijie, GUI Liangjin, SU Ruiyi. Research and development of automotive lightweight technology[J]. Journal of Automotive Safety and Energy, 2014, 5(1): 1–16. |
| [3] | 张鉴, 张新平, 袁广银, 等. 不同准晶含量Mg-Zn-Y-Zr合金的高温热压缩变[J]. 中国有色金属学报, 2009, 19(5): 793–799. ZHANG Jian, ZHANG Xinping, YUAN Guangyin, et al. Hot deformation behavior of Mg-Zn-Y-Zr base alloys with different contents of quasicrystal[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(5): 793–799. |
| [4] | XIA Xiangsheng, CHEN Qiang, HUANG Shuhai, et al. Hot deformation behavior of extruded Mg-Zn-Y-Zr alloy[J]. Journal of Alloys and Compounds, 2015, 644: 308–316. DOI: 10.1016/j.jallcom.2015.04.217 |
| [5] | LUO Z P, SONG D Y, ZHANG S Q. Strengthening effects of rare earths on wrought Mg-Zn-Zr-RE alloys[J]. Journal of Alloys and Compounds, 1995, 230(2): 109–114. DOI: 10.1016/0925-8388(95)01893-X |
| [6] | 栾娜, 李落星, 李光耀, 等. AZ80镁合金的高温热压缩变形行为[J]. 中国有色金属学报, 2007, 17(10): 1678–1684. LUAN Na, LI Luoxing, LI Guangyao, et al. Hot compression deformation behaviors of AZ80 magnesium alloy at elevated temperature[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1678–1684. DOI: 10.3321/j.issn:1004-0609.2007.10.021 |
| [7] | SINGH A. Tailoring microstructure of Mg-Zn-Y alloys with quasicrystal and related phases for high mechanical strength[J]. Science & Technology of Advanced Materials, 2014, 15(4): 044803. |
| [8] | YAO Dandan, ZHANG Yingbo. The nano-eutectic in the microstructure of semisolid Mg-6Zn-1Y alloy[J]. Materials Letters, 2016, 166: 201–205. DOI: 10.1016/j.matlet.2015.12.070 |
| [9] | KWAK T Y, LIM H K, KIM W J. Hot compression characteristics and processing maps of a cast Mg-9.5Zn-2.0Y alloy with icosahedral quasicrystalline phase[J]. Journal of Alloys and Compounds, 2015, 644: 645–653. DOI: 10.1016/j.jallcom.2015.04.158 |
| [10] | ZHANG Lei, WANG Lidong, XU Fubiao, et al. Hot deformation behavior of Mg2B2O5 whiskers reinforced Al compoise[J]. Journal of Harbin Institute of Technology (New Series), 2014, 21(3): 117–120. |
| [11] | 于思荣, 黄志求. 漂珠/AZ91D镁合金复合材料的高温压缩变形行为[J]. 复合材料学报, 2015, 32(5): 1461–1468. YU Sirong, HUANG Zhiqiu. High-temperature compression deformation behavior of fly ash cenosphere/AZ91D Mg alloy composites[J]. Acta Materiae Compositae Sinica, 2015, 32(5): 1461–1468. |
| [12] | 黄光杰, 程虎. 3104铝合金流变应力行为[J]. 重庆大学学报, 2007, 30(1): 70–72. HUANG Guangjie, CHENG Hu. Flow stress behavior of 3104 aluminum alloy[J]. Journal of Chongqing University, 2007, 30(1): 70–72. DOI: 10.11835/j.issn.1674-4764.2007.01.017 |
| [13] | GUO Q, YAN H.G, ZHANG H, et al. Behavior of AZ31 magnesium alloy during compression at elevated temperatures[J]. Materials Science and Technology, 2005, 22(11): 1349–1354. |
| [14] | PRASAD Y V R K, SASIDHARA S. Hot working guide:A compendium of processing maps[M]. Metal Park. OH: ASM International, 1997 : 1-24. |
| [15] | SIVAKESAVAM O, PRASAD Y V R K. Hot deformation behavior of as-cast Mg-2Zn-1Mn alloy in compression a study with processing map[J]. Mater Sci Eng A, 2003, 362: 118–124. DOI: 10.1016/S0921-5093(03)00296-X |
| [16] | 张蓉, 钱书琨. AZ61镁合金高温变形行为及热加工图[J]. 特种铸造及有色金属, 2014, 34(1): 19–22. ZHANG Rong, QIAN Shukun. Hot deformation behavior and processing map of AZ61 magnesium alloy[J]. Special Casting and Nonferrous Metals, 2014, 34(1): 19–22. |
| [17] | 陈振华, 严红革, 陈吉华, 等. 镁合金[M]. 北京: 化学工业出版社, 2004: 10-18. |
 2017, Vol. 25
2017, Vol. 25


