碳纤维织物是一种高性能的复合材料增强体，具有比强度比模量高、耐高温、耐腐蚀、可设计性强和抗疲劳性能好等优点，已经广泛应用于航天航空、国防军工领域^[1-2].近年来，国内外学者提出了复合材料冲压成形工艺^[3]，这为碳纤维编织复合材料大批量、高效率、低成本生产提供了新的契机.但是，复合材料织物在冲压成形中涉及纱线间的相互作用、纤维转动和再分配，导致其成形力学和变形机理非常复杂^[4-5].深入理解编织复合材料的力学特性和变形机理有利于后续本构开发和成形仿真工作的开展，因此，对碳纤维织物进行力学试验和成形实验研究具有重要的理论意义和工程应用价值.

国内外学者在编织复合材料的力学测试、成形实验和成形仿真方面进行了大量的研究.在力学测试方面，Cao等^[6]对编织复合材料剪切性能测试进行了规范和标准化.Launay等^[7-8]通过偏轴拉伸和镜框剪切试验研究了玻璃纤维织物的面内剪切性能，并对剪切力进行了正则化规定.Lebrun等^[9]通过镜框试验和偏拉试验对聚合物基编织复合材料在不同温度下的剪切行为进行了研究.在成形实验和仿真方面，张琦等^[3]设计了一种非等温加热半球冲压模具，讨论了碳纤维编织复合材料半球冲压在不同温度条件下的起皱和纤维缩进情况.Abbassi等^[10]和Khan等^[11]分别对编织纤维预浸料和干纤维编织布进行了双球冲压实验，并讨论了多层预浸料层间滑移情况及不同压边方式对成形件质量的影响.Peng等^[12]利用双球冲压数值模拟与实验相结合的方法，验证了其所提出的非正交本构模型的可靠性.

虽然这一领域已有了很多研究成果，但是无法全面揭示碳纤维织物的成形变形机理.本文对碳纤维织物展开单轴拉伸、双轴拉伸、镜框剪切试验和方盒冲压成形实验研究，旨在探索碳纤维织物在大变形条件下的力学行为和变形机理.

本文研究对象为碳纤维T300-3K平纹织物，其相关性能参数如表 1所示.

表1(Table 1)

表 1 碳纤维T300-3K平纹织物具体参数 Table 1 Parameters of the balanced plain carbon woven fabric 编织方式 面密度/ (g·m-2) 厚度/ mm 纱线宽度/ mm 杨氏模量/ GPa 抗拉强度/ GPa 单元尺寸/ mm×mm 1×1平纹 200 0.25 1.30 240 3.50 3.00×3.00

表 1 碳纤维T300-3K平纹织物具体参数 Table 1 Parameters of the balanced plain carbon woven fabric

碳纤维平纹织物的单轴拉伸选择矩形试样，试样长为230 mm，宽为115 mm.拉伸设备为Zwick/Roell 2 t万能拉伸试验机，如图 1所示.实验时，拉伸沿着织物的纱线方向，拉伸速度为2 mm/min，在室温下进行多次试验，输出单轴拉伸试验力-位移曲线.

图 Figure1(Figure Figure1)

图 1 单拉拉伸机和拉伸试样 Figure 1 Uniaxial tensile device and specimen

为了更好地了解碳纤维织物经纱和纬纱间的力学影响关系，对该碳纤维织物进行了不同双拉比的双轴拉伸试验.试验装置如图 2所示，该装置可以对2个垂直轴方向同时加载.为了避免面内剪切变形，实验试样设定为“十字正交形”，中心区域有效尺寸为50 mm×50 mm，拉伸臂长180 mm，宽50 mm.试验时通过控制经纱和纬纱方向的位移来实现不同的双拉比，拉伸速度为2 mm/min，在室温下进行多次试验，测得经纬方向的拉伸载荷-应变曲线，其中双拉比k=ε₂₂/ε₁₁(1代表经线方向，2代表纬向方向，当经线方向k=2时等效于纬线方向k=0.5).由于平纹织物的经向和纬向力学性能等效，因此本文只给出经线方向的拉伸载荷-应变曲线.

图 Figure2(Figure Figure2)

图 2 双轴拉伸机和拉伸试样 Figure 2 Biaxial tensile device and specimen

碳纤维织物的经向纤维和纬向纤维的夹角变化引起面内剪切变形，这种变形是织物复合材料成形过程中的主要变形模式^[13].本文通过镜框剪切(picture-frame)试验来研究碳纤维织物的剪切性能.镜框是由4个一样的钢臂构成并各自可以绕铰点自由转动，镜框尺寸为240 mm×240 mm，有效尺寸为180 mm×180 mm，该试验在Zwick/Roell 2t万能拉伸试验机上进行，拉伸速度10 mm/min，如图 3所示.

图 Figure3(Figure Figure3)

图 3 镜框剪切装置和剪切试样 Figure 3 Picture-frame device and shearing specimen before (a) and after (b) shear deformation

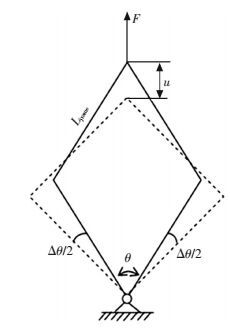
试验输出结果为剪切力-位移曲线，根据如图 4所示的试样几何变形原理，可以由式(1) 将力-位移曲线转化为剪切力-剪切角曲线.

图 Figure4(Figure Figure4)

图 4 镜框剪切示意图 Figure 4 Scheme diagram of picture frame

式中：L_frame为镜框臂长; u为拉伸位移; Δθ为剪切角.

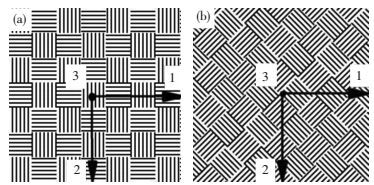
前文已经通过单轴拉伸、双轴拉伸和镜框剪切试验初步了解了该碳纤维织物的力学特性，下面将通过方盒冲压实验进一步探索其在成形中的力学行为和变形机理.剪裁160 mm×160 mm的正方形试样，剪裁方式有2种：一种沿纤维束(0°/90°)方向剪裁，见图 5(a); 另一种垂直纤维束(±45°)方向剪裁，见图 5(b).

图 Figure5(Figure Figure5)

图 5 实验中所用的平纹编织碳纤维布 Figure 5 Balanced plain carbon woven fabric: (a) 0°/90°; (b) ±45°

设计了如图 6所示的方盒冲压模具，方盒尺寸为60 mm×60 mm×30 mm，以模具横向对称轴为1轴，纵向对称轴为2轴，对称中心为原点，建立如图 6所示的坐标系来定义碳纤维织物相对于模具的纱线方向.实验时保证两种试样的坐标系与模具坐标系重合，实验在自主设计的热模压成形机上进行.

图 Figure6(Figure Figure6)

图 6 成形模具 Figure 6 Forming model

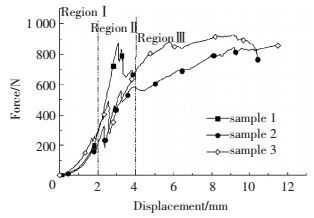
由图 7可知，该碳纤维织物单轴拉伸试验波动性很大，这是由于试样剪裁困难和拉伸过程中纤维断裂的情况不一致.此外，分析图 7可知，虽然该试验数据波动性较大，但仍可根据力-位移之间是否表现出线性相关性将拉伸力-位移曲线大致分为3个阶段：第1阶段，拉伸力和拉伸模量相对较小，这是由于该阶段编织纤维间有空隙和卷曲的纤维.第2阶段，随着变形的增加，拉伸力-位移曲线近似线性且拉伸模量很大，该区间属于正常拉伸阶段，在此阶段各试样的弹性模量相近; 第3阶段，当变形较大时，拉伸力-位移曲线出现严重的非线性，且拉伸模量相对第2阶段有所降低，这是因为该阶段出现了大量纤维的断裂.综上，该碳纤维织物的拉伸实验能够定性的描述碳纤维织物的力学特性，从整个拉伸阶段可以看出，该碳纤维织物沿纱线方向的拉伸性能具有高度的非线性力学行为.

图 Figure7(Figure Figure7)

图 7 单轴拉伸力-位移曲线 Figure 7 Uniaxial tensile load-displacement curve

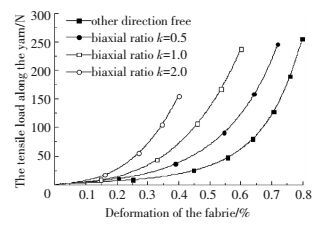
由图 8可知:与单轴拉伸相似，在同一双拉比下，当变形很小时，材料模量很低，表现为高度的非线性; 而在变形较大时，近似为线性.同时，随拉伸比增加，非线性区域减少，而且线性区域的材料弹性模量不随着拉伸比增大而增加.正如单轴拉伸试验分析指出，初始阶段非线性是由于存在纤维间隙和纤维卷曲，随双拉比的增加，由于纤维间的横向挤压程度增加可以有效减少纤维间隙和纤维卷曲，所以单轴拉伸时(另一方向没有约束)非线性区间最大，但是当大部分纤维都进入拉伸状态之后，材料性能由碳纤维材料本身决定.通过双轴拉伸试验可知，这种织物具有明显的双拉耦合效应，即一个方向的力学行为会对另一方向的力学行为产生影响.在碳纤维复合材料成形过程中，尤其是热冲压成形，由于压边圈施加压边力的作用，必须要考虑双拉耦合效应对成形质量的影响.

图 Figure8(Figure Figure8)

图 8 双轴拉伸力-应变曲线 Figure 8 Biaxial tensile load-strain curve

如图 9所示，剪切力-剪切角曲线呈现显著的非线性特征，整个过程大致可以分为3个阶段：第1阶段，由于纤维束自由旋转和偏移，外力主要克服纤维间的摩擦呈线性增加; 第2阶段，随着剪切角增大，经纬纤维相互挤压，剪切刚度增大，外力呈非线性增加; 第3阶段，当纤维达到剪切锁死角后，中心剪切区域出现起皱现象(如图 3(b)所示)，外力和剪切刚度剧烈增加，这是由于某些纤维处于拉伸状态.通过分析实验结果，拟合第1阶段的线性曲线，该拟合线与剪切力-剪切角曲线于第2阶段35°附近出现明显分离，对比多组实验数据可以粗略估计剪切锁死角约为35°.为进一步验证，在相同条件下进行了多次镜框剪切试验，实时监测纤维角度变化及起皱情况，记录试样开始发生起皱时刻的纤维剪切角，如表 2所示，进一步确定该织物的临界锁死角为35°.

图 Figure9(Figure Figure9)

图 9 镜框剪切力-剪切角曲线 Figure 9 Picture fame shear force vs shear angle curve

表2(Table 2)

表 2 镜框剪切试样起皱时刻的纤维剪切角 Table 2 Picture-fame shear angle on specimen wrinkling (°) 试样编号 1 2 3 4 5 平均 起皱时刻的纤维剪切角 36.2 37.3 31.9 35.4 34.7 35.1

表 2 镜框剪切试样起皱时刻的纤维剪切角 Table 2 Picture-fame shear angle on specimen wrinkling (°)

通过观察发现，在成形过程中织物纤维主要通过转动进行重新排列和取向.成形实验结果如图 10所示，不同取向的试样可以成形不同轮廓形状的零件.

图 Figure10(Figure Figure10)

图 10 冲压模具和冲压成形件 Figure 10 Stamp die and formed part: (a) 0°/90°; (b) ±45°

比较图 10(a)和图 10(b)，可以直观地看出：±45°试样的成形件边界纤维缩进量比较均匀，在圆角过渡带没有出现起皱现象; 而0°/90°试样的成形件边界纤维缩进量极度不均匀，圆角过渡带由于剪切角超过临界剪切锁死角(35°)出现了起皱，成形零件的轮廓形状出现了类似于金属成形中的“制耳”现象，这客观反映了这种织物具有较强的各向异性.因此可根据零件几何形状选择合适纤维取向的织物，合理铺层，减少缺陷，优化成形零件的力学性能.

1) 碳纤维织物具有高度的非线性和各向异性力学特性，同时具有双拉耦合效应，即经线(纬线)方向的力学行为会影响纬线(经线)方向的力学行为，且双轴拉伸状态下的力-应变曲线的非线性区域随双拉比的增加而减小.

2) 剪切变形是成形过程中的主要变形模式，当剪切角达到“临界锁死角”时，纤维间产生剧烈的挤压，织物发生起皱现象，因此剪切锁死角可以用于预测起皱缺陷.

3) 同种织物不同纱线取向的试样表现出不同的成形性能，±45°织物相比0°/90°织物成形件边界缩进量更均匀，起皱趋势更小.因此可以根据零件几何形状选择合适纤维取向的织物，合理铺层，从而减少缺陷，优化成形零件的力学性能.

本文的研究成果为后续织物本构模型的构建及其成形仿真奠定了实验基础.