2. 机械制造系统工程国家重点实验室(西安交通大学),西安 710049
2. State Key Laboratory of Mechanical Manufacturing Systems EngineeringXi′an Jiaotong University, Xi′an 710049, China
叶片是风力发电机最为复杂和关键的零部件,叶片性能的好坏将会直接影响到风力发电机的效率和使用寿命.目前,大型风力发电机的叶片基本上由各种复合材料制成,叶片与复合材料技术有着密切的联系.为了实现叶片经济效益的最大化,在叶片结构设计阶段,叶片的模型设计和铺层结构优化设计显得尤为关键,因此,精确地创建叶片的三维模型以及铺层结构是对叶片进行模拟分析的首要条件.目前,通常将叶片分为前缘、后缘、腹板、主梁和叶根5个结构进行建模,通过铺层设计原则[1]以及遗传算法[2]等对叶片各个结构分别进行铺层优化,最终得到最优铺层角度以及层数.
关于叶片的建模以及铺层优化问题,国内外很多学者都对此进行了研究:Monroy等[3]针对低速风机叶片,采用有限元原理进行结构分析,根据研究提出新的设计方式,并分析其优越性; 西南交通大学的王静[4]针对叶片精准建模,对模型进行模态分析,位移及局部应变方面的验证; 华北电力大学的李琪[5]对1.5 MW的风机叶片进行研究,设计了三维叶片模型的铺层,完成静力、模态和线性屈曲等分析.陈园[6]在对层压板结构进行参数化设计的基础时,采用遗传算法对复合材料结构全局优化的方法.冯消冰等[2]通过使用遗传算法对叶片的腹板、叶根以及梁帽进行了铺层优化.
本文利用Matlab中的优化函数fmincon对轴向因子以及周向因子进行优化计算,从而得到弦长和扭角的对应关系,最终建立更加精确的叶片模型.通过UG将模型导入ABAQUS,将叶片分为10个截面进行铺层,利用GH Bladed软件,计算额定转速下叶片表面载荷,以及叶根部位的复合材料的层间力,最后对叶片不同部位应力和应变的变化规律进行分析说明.
1 叶片模型设计参照国内2 MW风力发电机叶片运行参数,本文选用三叶片风机,叶片数B=3,选取叶尖速比[6] λ0=8.
1.1 翼型选择风机的运行效率与可靠性与翼型的气动性能密切相关,为了设计出具有更大风能捕获能力和低气动载荷的高性能叶片[7],在风电应用初期阶段,叶片外形比较小,载荷较低,对翼型的要求很低,主要选择低速航空翼型,如NACA44系列和NACA63-2系列翼型等[8].自20世纪80年代起,欧美国家陆续进行了风力机先进翼型的研究,研制了一批专用风力机翼型,如德国Aerodyn公司的AE02系列翼型、荷兰的DU翼型族、瑞典的FFA翼型族.其中, 荷兰的Delft大学先后发展了相对厚度15%~40%的DU系列翼型,而且在功率350~3 500 kW的风力机上广泛应用,本文选用DU系列的翼型,翼型如图 1所示.
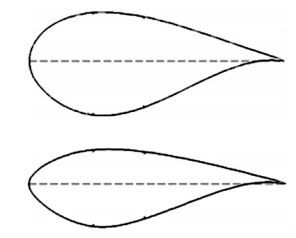
|
图 1 DU40、DU30翼型 Figure 1 The airfoil shapes of DU40 and DU30 |
本文参考国内2 MW风机的各项性能参数,设计风机叶片.因此, 风轮直径可按式(1) 进行估算:
| $\begin{array}{l} \quad \quad \quad D = \sqrt {\frac{P}{{{C_p}{\nu ^3}\frac{\rho }{2}\frac{{\rm{\pi }}}{4}\eta }}} = \\ \sqrt {\frac{{2{\rm{ }}000{\rm{ }}000}}{{0.45 \times {{11.4}^3} \times \frac{{1.225}}{2} \times \frac{{\rm{\pi }}}{4} \times 0.81}}} \approx 85.8. \end{array}$ | (1) |
式中:P为风机输出功率; CP为风能利用系数, 0.4~0.45;η为传动链和发电机效率, 为0.81;ρ为空气密度,1.225 kg/m3; ν为额定风速,11.4 m/s.
1.3 叶片长和扭角设计风机叶片外形复杂,总体表现为展向扭曲,而且在展向方向上弦长与扭角也大小迥异,不能够简单地将它们的特点进行描述,所以在研究中多采用“分段”法,即沿展向将叶片划分许多“截面”,对每个“截面”的数据进行计算,随后对数据分析、拟合.
本文基于动量理论进行计算,利用Matlab中的优化函数fmincon进行优化计算,优化目标为使风能的转换效率达到最大值,通过优化目标函数公式(2),条件方程为公式(3),利用迭代法计算轴向因子a和周向因子b.
优化目标函数:
| $\frac{b}{{1 - b}} = \frac{{BC{C_{\rm{L}}}}}{{4{\rm{\pi }}R{\rm{ }}(\sin \phi )}}.$ | (2) |
条件方程:
| $b\left( {1 + b} \right){\lambda ^2} = a\left( {1 + a} \right).$ | (3) |
式中:
其优化步骤为:1) 根据叶素理论,沿叶片展向分成若干等截面; 2) 针对每截面,求解得出各个截面的轴向因子a、周向因子b和叶梢损失系数F; 3) 计算每个截面的流倾角,并根据β=I-α,计算每个截面的扭角; 4) 计算出各个截面处的弦长; 5) 对计算结果进行改进; 6) 根据改进结果进行修正模型、建模.
利用Matlab迭代分析并进行曲线拟合,结果见图 2~5,可以看出,经过拟合,曲线过渡光滑平稳.

|
图 2 轴向诱导因子展向变化曲线 Figure 2 The curve of axial inducing factors |
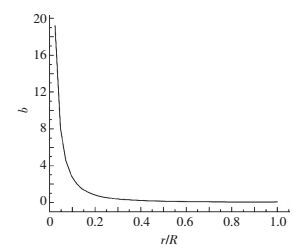
|
图 3 周向诱导因子展向变化曲线 Figure 3 The curve of circumferential inducing factors |

|
图 4 扭角展向变化拟合曲线图 Figure 4 The fitting curve of the spanwise change of torsion angle |

|
图 5 弦长展向变化拟合曲线图 Figure 5 The fitting curve of the spanwise change of chord |
由于风机叶片模型复杂,以及FEA软件建模效果的局限性,必须借用三维软件完成叶片精确模型的设计,本文利用表 1中计算的叶片弦长c和扭角θ的值,在UG中对导入翼型进行缩放和扭转,完成叶片截面图的创建,利用样条曲线连接各个翼型,并建立主梁,最终模型如图 6所示.
| 表 1 Matlab计算数据(部分) Table 1 Matlab computing data (part) |
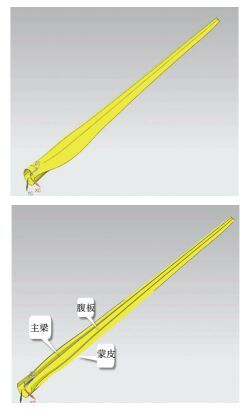
|
图 6 叶片的三维模型 Figure 6 3D model of blade |
本文采用目前常用的玻璃钢材料E-玻璃纤维增强环氧树脂基复合材料.
2.2 叶片铺层设计在叶片运行过程中,由于环境对叶片各个部位施加的载荷不同,通常对叶片进行块化处理,将叶片分为前缘、后缘、腹板和主梁4种结构.参照国内外和以往铺层设计经验[8~14],其设计原则如下[12].
1) 为了最大限度地利用纤维轴向的高性能,应用0°铺层承受轴向载荷; ±45°铺层用来承受剪切载荷,即将剪切载荷分解为拉、压分量来布置纤维承载; 90°铺层用来承受横向载荷,以避免树脂直接受载.
2) 为了提高叶片的抗屈曲性能,除布置较大比例的0°铺层外,也要布置±45°铺层,以提高结构受压稳定性.
3) 构件应包含4种铺层,一般在0°、±45°层板中加入90°的铺层,构成正交异性板.
对叶片不同结构进行铺层设计,表 2~5分别为叶片不同部位的铺层顺序表.
| 表 2 叶片前缘铺层设计 Table 2 The layer design of blade leading edge |
| 表 3 叶片后缘铺层设计 Table 3 The layer design of blade trailing edge |
| 表 4 叶片主梁铺层设计 Table 4 The layer design of blade grider |
| 表 5 叶片腹板铺层设计 Table 5 The layer design of blade web |
图 7为利用ABAQUS对风机叶片不同部位建立铺层后腹板和主梁的效果图,从效果图中可以直观地看出不同位置的铺层差异.

|
图 7 ABAQUS铺层效果图 Figure 7 Layer rendering of ABAQUS |
由于风机所处环境复杂,叶片表面载荷难以准确的计算和测量,一般都是利用风机专用分析软件GH Bladed计算叶片表面的数据,本文利用bladed软件计算风机叶片不同部位在额定风速下的载荷[16],将分析所得载荷加载在叶片表面,叶片加载位置和加载力与扭矩的大小如图 8和表 6所示(在ABAQUS中通过选择节点和曲线添加载荷).

|
图 8 载荷添加位置示意图 Figure 8 Schematic diagram of load position |
| 表 6 叶片表面不同位置载荷 Table 6 The different position loads on the surface of the blade |
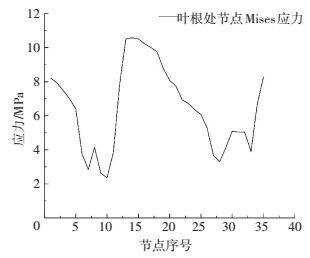
由图 9叶片应力云图可以看出,应力最大的位置出现在根部,而且分布较为复杂,其最大值为15 MPa.此外,应力从叶根部位向叶尖部位逐渐减小,各分块的处节点应力值的变化如图 10~15所示.图 10为叶片根部截面的应力变化规律曲线,从图中可以看出根部的应力基本都保持在兆帕级以上,而且力的大小呈现一个正态分布的形式,其原因是叶片的承受力主要集中在迎风面,所以迎风面的压力较大,造成叶根部位迎风面的压力大于压力面.
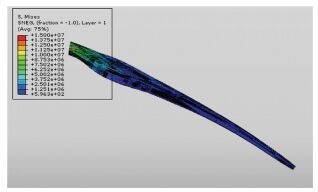
|
图 9 叶片应力云图 Figure 9 The equivalent stress of blade |
|
图 10 叶片叶根环形应力变化 Figure 10 Blade root ring stress |
|
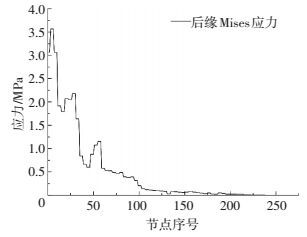
图 11 叶片后缘叶根到叶尖的应力变化 Figure 11 Trailing edge of blade root to tip stress changes |
|
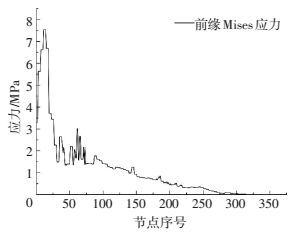
图 12 叶片前缘叶根到叶尖的应力变化 Figure 12 The stress changes of blade leading edge root to leaf tip |

|
图 13 叶片主梁叶根到叶尖的应力变化 Figure 13 The stress changes of blade girder root to leaf tip |
|
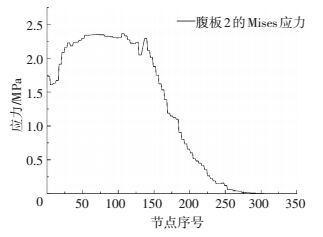
图 14 叶片前缘腹板叶根到叶尖的应力变化 Figure 14 The stress changes of blade leading edge web root to leaf tip |

|
图 15 叶片后缘腹板叶根到叶尖的应力变化 Figure 15 The stress changes of variation of blade trailing edge web root to leaf tip |
图 10、图 11分别为后缘和前缘部位叶根到叶尖的应力变化曲线,可以看出:叶片表面的应力是从叶根向叶尖部位逐渐变小,而且在局部地方还有应力集中; 后缘部位的应力突变的部位比前缘的多,而且变化更为严重,这是由于叶片翼型的后缘曲率较大,变化快,造成后缘应力集中部位较多.
图 12、图 13和图 14分别为叶片主梁、靠近前缘部位的腹板和靠近后缘部分的腹部中部分节点的叶根到叶尖的应力变化曲线.由图 12可以看出,叶片主梁结构叶根到叶尖的应力变化缓慢; 而图 13和图 14说明,接近前缘的腹板与接近后缘的腹板上的应力变化有着很大的差异,靠近前缘部位的腹板应力变化缓慢,但应力水平比较高,而靠近后缘部位的腹板,应力水平比较低,而且变化不规则.
3.2 叶片根部复合材料应力变化规律分析图 16~19分别为叶根部位45°、-45°、90°和0°铺设角度的Mises应力云图,可以看出,由于复合材料的铺设角度不同,层和板的应力存在明显的差异,最大应力出现在45°的铺层中,为15.2 MPa,出现在第2层,然后是90°的铺层,为15.19 MPa,出现在第58层,再然后为45°铺层,为15 MPa,出现在第1层,0°铺层的应力最小,是9.7 MPa,出现在第52层.从应力云图中可以看到,随着层数的变化,叶片上的应力差异在逐渐减小,而且应力最大的部位向叶片根部连接端移动.
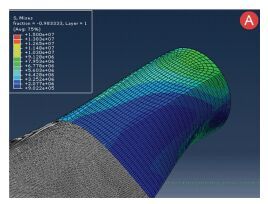
|
图 16 叶根部位45°Mises应力云图 Figure 16 The mises stress of 45° in blade root |
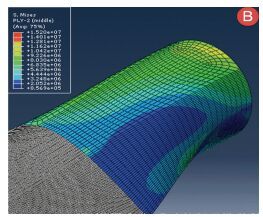
|
图 17 叶根部位-45°Mises应力云图 Figure 17 The mises stress of -45° in blade root |

|
图 18 叶根部位90°Mises应力云图 Figure 18 The mises stress of 90° in blade root |

|
图 19 叶根部位0°Mises应力云图 Figure 19 The mises stress of 0° in blade root |
图 20为叶根部位铺层自外向内的应力变化曲线,叶片根部部位单层层合板上的最大应力呈现周期性变化规律,与叶片根部铺层的铺设基本一致,虽然相同角度不同位置的铺层上的应力有一定差异,但总体上差异远小于铺设角度的差别.图 21为其最小应力的位置改变曲线,由图可知,最小应力出现在中间靠近叶片内腔的位置,这是因为叶片受到外力的作用导致应力变化向内转移.

|
图 20 叶根部位不同铺层的应力变化曲线 Figure 20 The stress change curve of the different layer of blade root |
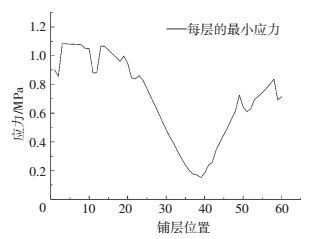
|
图 21 叶根部位不同铺层的最小应力变化曲线 Figure 21 The minimum stress change curve of the different layer of blade root |
运用翼型设计软件Profili、分析软件Matlab以及三维制图软件UG和ABAQUS,能够创建更贴近实际工程的风机叶片模型,通过GH Bladed计算载荷以及对叶片加载分析后得到以下结论:
1) 在额定风速下,由于叶片的承受力主要集中在迎风面,导致叶片根部应力的大小呈现一个正态分布的形式,应力大小基本保持在兆帕级,最大应力为15 MPa.
2) 通过对叶片根部不同铺层应力分析可知:由于复合材料的铺设角度不同,层和板的应力存在明显的差异,最大应力出现在45°的铺层中,为15.2 MPa; 第二是90°的铺层,为15.19 MPa; 之后为45°铺层,为15 MPa; 0°铺层的应力最小,是9.7 MPa.
3) 对叶片根部复合材料层间力分析可知,-45°铺层的层间应力最大,而且应力跟随铺设角度的不同而成周期性变化.
| [1] | 张军. 大型风机叶片结构分析与铺层优化[D]. 无锡: 江南大学, 2013: 21-60. |
| [2] |
冯消冰, 黄海, 王伟. 大型风机复合材料叶片铺层优化设计[J]. 玻璃钢/复合材料, 2013(3): 3–7.
FENG Xiaobing, HUANG Hai, WANG Wei. Ply optimization of composite materials for blade in wind turbine[J]. FRE/CM, 2013(3): 3–7. |
| [3] | MONROY A C, SUTCLIFFE M P F, ASHBY M F, et al. Design methodology for composite structures: a small low air-speed wind turbine blade case study[J]. Materials and Design, 2012, 36: 296–305. DOI: 10.1016/j.matdes.2011.11.033 |
| [4] | 王静. 复合材料风机叶片结构校核理论及数值仿真方法研究[D]. 成都: 西南交通大学, 2011: 42-60. |
| [5] | 李琪. 复合材料风电叶片结构设计及有限元分析[D]. 北京: 华北电力大学, 2013: 25-42. |
| [6] | 陈园. 风力发电机叶片三维建模及有限元动力学分析[D]. 西安: 西安理工大学, 2008: 23-41. |
| [7] |
铁庚, 祁文军. 水平轴风力机叶片翼型的气动特性数值模拟[J]. 流体机械, 2013, 41(3): 29–33.
TIE Geng, QI Wenjun. Numerical simulation on the aerodynamic performance of aerofoil of horizontal wind turbine blade[J]. Fluid Machinery, 2013, 41(3): 29–33. |
| [8] | 贺德馨. 风工程与工业空气动力学[M]. 北京: 国防工业出版社, 2006: 1, 104-118. |
| [9] | COX K, ECHTERMEYER A. Structural design and analysis of a 10MW wind turbine blade[J]. Energy Procedia, 2012, 24: 194–201. DOI: 10.1016/j.egypro.2012.06.101 |
| [10] | KONG C, BANG J, SUGIYAMA Y. Structural investigation of composite wind turbine blade considering various load cases and fatigue life[J]. Energy, 2005, 30(11): 2101–2114. |
| [11] | YI Hua, KASAVAJHALA A R M, GU Linxia. Elastic-plastic analysis and strength evaluation of adhesive joints in windtur bine blades[J]. Composites: Part B, 2013, 44: 650–656. DOI: 10.1016/j.compositesb.2012.02.001 |
| [12] | MEZIANE M, ABDELAZIZ H, TOUNSI A. An efficient and simple refined theory for buckling and free vibration of exponentially graded sandwich plates under various boundary conditions[J]. Journal of Sandwich Structures & Materials, 2014, 16(3): 293–318. |
| [13] | HUH Y H, LEE J H, KIM D J, et al. Effect of stress ratio on fatigue life of GFRP composites for WT blade[J]. Journal of Mechanical Science and Technology, 2012, 26(7): 2117–2120. DOI: 10.1007/s12206-012-0526-0 |
| [14] |
李祚军, 张娟, 王佩艳, 等. T700/3234碳纤维层合板的拉伸疲劳特性分析[J]. 机械设计与制造, 2013(10): 4–6.
LI Zuojun, ZHANG Juan, WANG Peiyan, et al. Tensile and fatigue properties of T700/3234 carbon fiber reinforced composite laminates[J]. Machinery Design & Manufacture, 2013(10): 4–6. DOI: 10.3969/j.issn.1001-3997.2013.10.002 |
| [15] | VARVANI-FARAHANI A, SHIRAZI A. A fatigue damage model for (0/90) FRP composites based on stiffness degradation of 0° and 90° composite plies[J]. Journal of Reinforced Plastics & Composites, 2007, 26(13): 1319–1336. |
| [16] | 于彬. 极端环境载荷对复合材料风机叶片特性影响分析[D]. 新疆: 新疆大学, 2015: 7-14. |
 2017, Vol. 25
2017, Vol. 25


