叠层制造(Laminated Object Manufacturing, LOM)为广义的工件逐层制备技术的总称,涵盖广泛,包括传统的狭义分层实体成形技术,以三维打印为代表的增材制造技术[1],为表面改性在基体上制备涂层的技术[2],为功能性要求使性能不同的组分材料逐层制备的梯度功能材料多层结构[3].这些技术和工艺之所以归类为广义的叠层制造,在于它们有一个共同的工艺特征:“分层制备,逐层叠加”.就结构特征而言,表现为单一材料或多种材料的多层结构;就制备环境而言,大都在高温下成形[4],冷却后产生热残余现象.
引起热残余现象的主要原因有:1) 各层材料性能差异;2) 成形过程中逐步梯度降温.以往对叠层制造热残余的研究主要集中于第一种原因.为便于导出解析解,前期所有理论研究均基于“同步降温”假设[5-9],认为所有的层制备完成后均从制备温度同时降至室温,依据这个假设,只有当各层材料不同时才会产生热残余应力.这类理论早期仅考虑轴向的变形和应力,所得应力偏大[5];继而考虑弯曲变形(翘曲)[6-9],且建立数值模型[10-12],精度有所改善.但由于“同步降温”假设与制备工艺中实际存在的梯度降温不符,因此,计算结果与实际有显著差距.王维等从多工艺参数角度分析了翘曲产生的原因[13].闫旭日等认为,LOM中间树脂热溶胶的冷却固化是箔片成形后翘曲的原因,力学机理为层间剪应力[14].王天明等仅就新堆积层冷却引起的翘曲给出解析解[15].另一方面,对于三维打印、粉末激光烧结、熔融堆积成形等叠层制备工艺,在同一层的平面内是由扫描逐行成形的.因此,在同一层平面内,也会因扫描前后出现降温梯度而产生热残余现象.因此,目前尚缺乏针对制备全过程热残余机理的研究.
然而,即使是同一种材料叠层制备(如三维打印),也会因制备的先后而形成降温梯度,冷却后工件仍会产生明显的弯曲变形.而依据同步降温理论,不应该出现弯曲变形.因此,考虑叠层的制备过程及其梯次降温,是精确分析叠层制造热残余现象的正确途径.本文依据实际制备工艺提出“梯度降温”概念,充分考虑成形过程中逐次降温,沿长度方向和厚度方向形成温度梯度,成形结束后再整体降至室温.本文基于梯度降温的实际,将分别讨论在层平面内和厚度方向梯度降温引起的残余变形和应力.
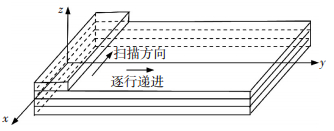
图 1为叠层梁制备示意图,L为工件长,B为宽,H为厚.第i层厚度为hi,上下表面的z坐标为zi-1和zi.喷嘴沿x方向进给扫描,沿y方向递进,沿z方向形成叠层结构.制备温度与室内温度相差ΔT.为便于得到解析解,需对降温过程作一定的合理简化,为此, 对制备过程中形成的降温梯度作如下假设:1) 沿厚度每一层冷却降温幅度不同,形成热残余应力σy;2) 沿y方向每条扫描的降温幅度不同,形成热残余应力σx;3) 同一条扫描不考虑降温梯度.即只考虑沿y和z方向有降温梯度Δty和Δtz.
|
图 1 几何结构 Figure 1 Geometry |
在此假设下,在每一层的平面(xy)上,每一条扫描因时间差异出现沿y方向的降温梯度,因而沿x方向会产生不同的收缩率,形成热残余应力σx;沿着厚度(z)方向,每一层扫描因时间的差异出现沿z方向的降温梯度,因而沿y方向会产生不同的收缩率且发生弯曲,形成热残余应力σy.因此,下文将整个热残余产生过程分解为两部分,分两节讨论其解析解.
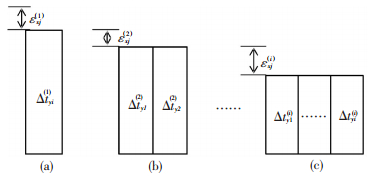
1 水平(xy)层面热残余分析以第j层为例,假设工件在第j层平面内共需要扫描m次,每次扫描宽度为l,厚度为h.第j层的弹性模量为Ej,热膨胀系数为αj.成形过程中,由于逐条扫描,各条逐次降温收缩,沿着y方向存在明显的温度梯度,扫描完成后再整体降至室温.为便于分析,将第j层扫描制备过程及降温过程近似分解成图 2中的几个步骤:
|
图 2 逐条扫描降温和变形过程 Figure 2 Cooling and deformation process during scanning |
1) 第1行成形完毕制备第2行时(图 2(a)),假设第1行已降温Δty1(1),此时第1行热应变为
| $ \varepsilon _{xj}^{(1)} = {\alpha _j}\Delta t_{y1}^{(1)}. $ | (1) |
因第1行为自由变形,产生的热内力N1(1)=0.
2) 第2行成形完毕制备第3行时(图 2(b)),假设第1行已累计降温Δty1(2),第2行降温Δty2(2),当次产生的热应变为εxj(2),由于两行温度梯度的差异,由此产生的热内力为
| $ \begin{array}{l} N_1^{(2)} = {E_j}lh(\varepsilon _{xj}^{(2)} + \varepsilon _{xj}^{(1)} - {\alpha _j}\Delta t_{y1}^{(2)}),\\ N_2^{(2)} = {E_j}lh(\varepsilon _{xj}^{(2)} - {\alpha _j}\Delta t_{y2}^{(2)}). \end{array} $ | (2) |
由截面内力和为零(N1(2)+N2(2)=0),解得
| $ \varepsilon _{xj}^{(2)} = \frac{{ - \varepsilon _{xj}^{(1)} + {\alpha _j}(\Delta t_{y1}^{(1)} + \Delta t_{y2}^{(2)})}}{2}. $ | (3) |
3) 依此类推,第i行成形完毕制备第i+1行时(图 2(c)),1至i行的累计降温Δtyk(i)(k=1, …, i),当次产生的热应变为εxj(i),由此各行产生的热内力为
| $ N_k^{(i)} = {E_j}lh(\sum\limits_{r = k}^i {{\varepsilon ^{(r)}}} - {\alpha _j}\Delta t_{yk}^{(i)}). $ | (4) |
由截面内力和为零
| $ \begin{array}{c} \varepsilon _{xj}^{(i)}\frac{1}{i}\left( { - \sum\limits_{k = 1}^{i - 1} {\sum\limits_{r = k}^{i - 1} {\varepsilon _{xj}^{(r)}} } + {\alpha _j}\sum\limits_{k = 1}^i {\Delta t_{yk}^{(i)}} } \right)\\ \left( {i = 2, \ldots ,m - 1} \right){\rm{ }}. \end{array} $ | (5) |
4) 当完成最后一行制备后,工件将整体降至室温,则当次产生的热应变(εxj(m))为
| $ \varepsilon _{xj}^{(m)} = - \frac{1}{m}\sum\limits_{k = 1}^{m - 1} {\sum\limits_{r = k}^{m - 1} {\varepsilon _{xj}^{(r)}} } + {\alpha _j}\Delta T. $ | (6) |
成形过程中各次产生的热残余应变εxj(i)(i=1, …, m)分别由式(1)、(5)、(6) 依次计算获得.因此,第i行最终产生的累计应变为
| $ \sigma _{xj}^{(i)} = {E_j}(\sum\limits_{r = i}^m {\varepsilon _{xj}^{(r)}} - {\alpha _j}\Delta T). $ | (7) |
对于多层结构,高温制备冷却后,工件会发生轴向(y)收缩变形和横向弯曲变形.一般简化的计算仅考虑热残余轴向变形及其应力,可能产生很大的误差;更合理的研究考虑了同步降温假设下涂层的弯曲变形,但均未考虑实际存在的梯度降温现象.本文基于梯度降温的实际,将分别讨论这两种变形和应力以及它们的合成.
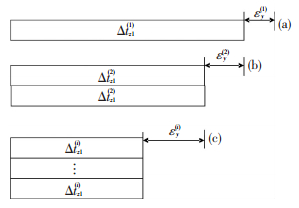
2.1 轴向(y)变形和应力设工件(叠层梁)共n层.成形过程中,由于各层加工的时差,各层逐次降温,沿厚度方向形成明显的温度梯度,成形完成后再整体降至室温.为便于分析,将叠层的制备过程及其降温过程近似分解成以下步骤.
1) 第1层成形完毕制备第2层时(图 3(a)),假设第1层已降温Δtz1(1),此时第1层热应变为
| $ \varepsilon _y^{(1)} = {\alpha _1}\Delta t_{z1}^{(1)} $ | (8) |
|
图 3 逐层降温和轴向变形过程 Figure 3 Cooling and axial deformation process through layers |
因第1层为自由变形,产生的热内力N1(1)=0.
2) 第2层成形完毕制备第3层时(图 3(b)),假设第1层已累计降温Δtz1(2),第2层降温Δtz2(2),当次产生的热应变为εy(2),由于两层材料和温度梯度的差异,由此产生的热内力为
| $ \left\{ \begin{array}{l} N_1^{(2)} = {E_1}{h_1}\left( {\varepsilon _y^{(2)} + \varepsilon _y^{(1)} - {\alpha _1}\Delta t_{z1}^{(2)}} \right),\\ N_2^{(2)} = {E_2}{h_2}(\varepsilon _y^{(2)} - {\alpha _2}\Delta t_{z2}^{(2)}). \end{array} \right. $ | (9) |
由截面内力和为零(N1(2)+N2(2)=0),解得
| $ \varepsilon _y^{(2)} = \frac{{ - {E_1}{h_1}\varepsilon _y^{(1)} + {E_1}{h_1}{\alpha _1}\Delta t_{z1}^{(2)} + {E_2}{h_2}{\alpha _2}\Delta t_{z2}^{(2)}}}{{{E_1}{h_1} + {E_2}{h_2}}}. $ | (10) |
3) 依此类推,第i层成形完毕制备第i+1层时(图 3(c)),1至i层的累计降温Δtzk(i)(k=1, …, i),当次产生的热应变为εy(i),由此各层产生的热内力为
| $ N_k^{(i)} = {E_k}{h_k}(\sum\limits_{r = k}^i {\varepsilon _y^{(r)}} - {\alpha _k}\Delta t_{zk}^{(i)}). $ | (11) |
由截面内力和为零(
| $ \begin{array}{c} \varepsilon _y^{(i)} = \frac{{ - \sum\limits_{k1}^{i - 1} {{E_k}{h_k}} \sum\limits_{r = k}^{i - 1} {\varepsilon _y^{(r)}} + \sum\limits_{k = 1}^i {} {E_k}{h_k}{\alpha _k}\Delta t_{zk}^{(i)}}}{{\sum\limits_{k = 1}^i {{E_k}{h_k}} }}\\ \left( {i = 2, \ldots ,n - 1} \right). \end{array} $ | (12) |
4) 当完成最后一层制备后,工件将整体降至室温,则当次产生的热应变(εy(n))为
| $ \varepsilon _y^{(n)} = \frac{{ - \sum\limits_{k = 1}^{n - 1} {{E_k}{h_k}} \sum\limits_{r = k}^{n - 1} {\varepsilon _y^{(r)}} + (\sum\limits_{k = 1}^n {{E_k}{h_k}{\alpha _k}} )\Delta T}}{{\sum\limits_{k = 1}^n {{E_k}{h_k}} }}. $ | (13) |
成形过程中各次产生的热残余应变εy(i)(i=1, …, n)分别由式(8)、(12)、(13) 依次计算获得.因此,第i层最终产生的累计轴向应变为
| $ \sigma _{yi}^N = {E_i}(\sum\limits_{k = i}^n {\varepsilon _y^{(k)}} - {\alpha _i}\Delta T). $ | (14) |
冷却后第i层的弯曲热残余应力σyiM为
| $ \sigma _{yi}^M = {E_i}K\left( {z + \delta } \right). $ | (15) |
同样地,对于纯弯曲问题,由弯曲应力σyiM形成的截面力之和为零,而截面弯矩不为零,记为M.即有
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^n {\int_{{z_{i - 1}}}^{{z_i}} {{E_i}K\left( {z + \delta } \right){\rm{d}}z} = 0,} \\ \sum\limits_{i = 1}^n {\int_{{z_{i - 1}}}^{{z_i}} {{E_i}K{{\left( {z + \delta } \right)}^2}{\rm{d}}z} = M} . \end{array} \right. $ | (16) |
解得
| $ \delta = \frac{{ - \sum\limits_{i = 1}^n {{E_i}{h_i}({z_i} + {z_{i - 1}})} }}{{2\sum\limits_{i = 1}^n {{E_i}{h_i}} }}, $ | (17) |
| $ M = \frac{1}{3}K\sum\limits_{i = 1}^n {{E_i}{h_i}({z^2}_i + {z_i}{z_{i - 1}} + {z^2}_{i - 1} - 3{\delta ^2})} . $ | (18) |
在梁的横截面,除了由弯曲应力σyiM形成的弯矩M,前面所得的各层轴向应力σyiN形成的弯矩也不为零,但两者的和必须为零,因此, 有
| $ M + \sum\limits_{i = 1}^n {\int_{{z_{i - 1}}}^{{z_i}} {\sigma _{yi}^N\left( {z + \delta } \right){\rm{d}}z} } = 0. $ | (19) |
由此解得曲率(K)为
| $ K = \frac{{ - 3\sum\limits_{i = 1}^n {\sigma _{yi}^N} {h_i}({z_i} + {z_{i - 1}})}}{{2\sum\limits_{i = 1}^n {{E_i}{h_i}({z^2}_i + {z_i}{z_{i - 1}} + {z^2}_{i - 1} - 3{\delta ^2})} }}. $ | (20) |
由式(17) 和(20) 分别得到了两个表征弯曲变形的几何参数δ和K,再由式(15) 可计算弯曲变形引起的热残余应力σyiM.
2.3 应力合成总的热残余应力σyi为轴向拉伸应力σyiN(式(14))和横向弯曲应力σyiM(式(15))之和,
| $ \begin{array}{l} {\sigma _{yi}} = \sigma _{yi}^N + \sigma _{yi}^M = \\ \quad {E_i}\left[ {\left( {\sum\limits_{k = i}^n\varepsilon _y^{(k)} - {\alpha _i}\Delta T} \right) + K\left( {z + \delta } \right)} \right]. \end{array} $ | (21) |
根据曲率可以计算梁的挠曲变形.因热残余变形沿轴向对称,若以梁的中点为坐标x的原点,根据对称性其弯曲变形的挠度w为
| $ w = \frac{M}{{2D}}{x^2} = \frac{1}{2}K{x^2}\;\;\;\;\left( { - \frac{L}{2} \le x \le \frac{L}{2}} \right). $ | (22) |
若为同一种材料叠层成形,且各层等厚度,则各次产生的轴向热应变式(8)、(12)、(13) 可简化为
| $ \left\{ \begin{array}{l} \varepsilon _y^{(1)} = \alpha \Delta t_{z1}^{(1)},\\ \varepsilon _y^{(i)} = \frac{1}{i}( - \sum\limits_{k = 1}^{i - 1} {\sum\limits_{r = k}^{i - 1} {\varepsilon _y^{(r)}} } + \alpha \sum\limits_{k = 1}^i {\Delta t_{zk}^{(i)}} )\\ \left( {i = 2, \ldots ,n - 1} \right),\\ \varepsilon _y^{(n)} = - \frac{1}{n}\sum\limits_{k = 1}^{n - 1} {\sum\limits_{r = k}^{n - 1} {\varepsilon _y^{(r)}} } + \alpha \Delta T. \end{array} \right. $ | (23) |
由式(17) 得δ=0,而表征弯曲变形的曲率简化为
| $ K = \frac{{ - 3\sum\limits_{i = 1}^n {\sigma _{yi}^N({z_i} + {z_{i - 1}})} }}{{2E\sum\limits_{i = 1}^n {(z_i^2 + {z_i}{z_{i - 1}} + z_{i - 1}^2)} }}. $ | (24) |
本文的广义叠层制备包涵多种制备工艺,不同的叠层制备工艺的降温梯度表现不同,即沿y和z方向降温梯度Δty和Δtz不同,可经实验测量得到.除了上述一般的降温梯度外,还有下文两种极端的工况.
3.1 无温度梯度工艺制备时成型室的环境温度趋近制备温度,如将多层箔片加树脂压制成形,可认为制备过程中无降温,又称为保温制备.待工件全部制备结束后,从成形室取出工件,同步降至室温.即取
| $ \left\{ \begin{array}{l} \Delta t_{yk}^{(i)} = 0{\rm{ }}\left( {k = 1, \ldots ,i,i = 1, \ldots ,m - 1} \right),\\ \Delta t_{yk}^{(m)} = \Delta T{\rm{ }}\left( {k = 1, \ldots ,m} \right),\\ \Delta t_{zk}^{(i)} = 0{\rm{ }}\left( {k = 1, \ldots ,i,i = 1, \ldots ,n - 1} \right),\\ \Delta t_{zk}^{(m)} = \Delta T{\rm{ }}\left( {k = 1, \ldots ,n} \right). \end{array} \right. $ | (25) |
因此,热残余解可以简化为如下形式.
1) 水平(xy)层面热残余分析
| $ \left\{ \begin{array}{l} \varepsilon _{xj}^{(i)} = 0{\rm{ }}\left( {i = 1, \ldots ,m - 1} \right),\\ \varepsilon _{xj}^{(m)} = {\alpha _j}\Delta T. \end{array} \right. $ | (26) |
各行的热残余应力σxj(i)均为零.
2) 叠层方向热残余分析
a)轴向热残余应变
| $ \left\{ \begin{array}{l} \varepsilon _y^{(i)} = 0\;\;\;\;\left( {i = 1, \ldots ,n - 1} \right),\\ \varepsilon _y^{(n)} = \frac{{\sum\limits_{k = 1}^n {{E_k}{h_k}{\alpha _k}} }}{{\sum\limits_{k = 1}^n {{E_k}{h_k}} }}\Delta T = \bar \alpha \Delta T. \end{array} \right. $ | (27) |
式中α为加权热膨胀系数(加权系数为各层截面刚度Eihi).因此,各层的轴向热残余应力为
| $ \sigma _{yi}^N = {E_i}(\bar \alpha - {\alpha _i})\Delta T. $ | (28) |
b)弯曲变形和应力
第i层的弯曲热残余应力为
| $ \sigma _{yi}^M = {E_i}K\left( {z + \delta } \right). $ | (29) |
式中弯曲几何参数δ和K简化为
| $ \delta = \frac{{ - \sum\limits_{i = 1}^n {{E_i}{h_i}({z_i} + {z_{i - 1}})} }}{{2\sum\limits_{j = 1}^n {{E_i}{h_i}} }}, $ | (30) |
| $ K = \frac{{ - 3\sum\limits_{i = 1}^n {{E_i}{h_i}({z_i} + {z_{i - 1}})(\bar \alpha - {\alpha _i})} }}{{2\sum\limits_{i = 1}^n {{E_i}{h_i}(z_i^2 + {z_i}{z_{i - 1}} + z_{i - 1}^2 - 3{\delta ^2})} }}\Delta T. $ | (31) |
第i层总的热残余应力σyi为轴向拉伸应力σyiN(式(28))和横向弯曲应力σyiM(式(29))之和
| $ \begin{array}{l} {\sigma _{yi}} = \sigma _{yi}^N + \sigma _{yi}^M = \\ \quad {E_i}[(\bar \alpha - {\alpha _i})\Delta T + K\left( {z + \delta } \right)]. \end{array} $ | (32) |
对一些叠层制备工艺,如熔融堆积成形工艺,固化冷却时间仅需数秒,而堆积一个层面所用时间远大于固化时间,因此,可视为立即从制备温度降到室温.即取
| $ \left\{ \begin{array}{l} \Delta t_{yk}^{(i)} = \Delta T{\rm{ }}\left( {k = 1, \ldots ,i,i = 1, \ldots ,m} \right),\\ \Delta t_{zk}^{(i)} = \Delta T{\rm{ }}\left( {k = 1, \ldots ,i,i = 1, \ldots ,n} \right). \end{array} \right. $ | (33) |
因此,热残余解可以简化为如下形式.
1) 水平(xy)层面热残余分析
| $ \varepsilon _{xj}^{(i)} = \frac{1}{i}{\alpha _j}\Delta T\;\;\;\;\left( {i = 1, \ldots ,m} \right). $ | (34) |
各行的热残余应力
| $ \sigma _{xj}^{(i)} = {E_j}{\alpha _j}\Delta T\left( {\frac{1}{i} + \ldots + \frac{1}{m} - 1} \right)\;\;\;\;\left( {i = 1, \ldots ,m} \right). $ | (35) |
2) 叠层方向热残余分析
a)轴向热残余应变
| $ \varepsilon _y^{(i)} = \frac{{{E_i}{h_i}{\alpha _i}}}{{\sum\limits_{k = 1}^i {{E_k}{h_k}} }}\Delta T\;\;\;\;\left( {i = 1, \ldots ,n} \right). $ | (36) |
因此,第i层的轴向热残余应力为
| $ \sigma _{yi}^N = {E_i}[\sum\limits_{k = i}^n {\frac{{{E_k}{h_k}{\alpha _k}}}{{\sum\limits_{r = 1}^k {{E_r}{h_r}} }}} - {\alpha _i}]\Delta T\;\;\;\;\left( {i = 1, \ldots ,n} \right). $ | (37) |
b)弯曲变形和应力
第i层的弯曲热残余应力σyiM仍见式(15).
4 算例 4.1 功能梯度材料制备两种组分材料(NiCoCrAlY和ZrO2)按不同比例配比的性能[7]见表 1,分5层制备,ZrO2组分的比例依次为0、25%、50%、75%、100%.考虑两种制备顺序,第一种制备顺序(顺序1) 的弹性模量和热膨胀系数依次下降;另一种制备顺序相反(顺序2),弹性模量和热膨胀系数依次上升.设制备温度为700 K,室温为300 K,温差为-400 K.工件厚度2 mm,长度50 mm.
| 表 1 材料性能 Table 1 roperties of materials |
先进行叠层方向热残余分析.为方便讨论,采用同一个算例来比较各种叠层制备工艺的热残余特征,沿厚度方向的降温梯度按4种模式考虑.
1) 模式1,同步降温假设(保温制备工艺):认为成形过程中各层均不降温,成形结束后所有层同时降至室温.
2) 模式2,均等梯度降温假设:取每一层的降温梯度为80 ℃.
3) 模式3,非均等梯度降温假设:认为刚噴涂完时迅速固化降温,降温幅度最大,取200 ℃;而后降温幅度变小,每隔1层降温40 ℃.
4) 模式4,瞬态降温假设(快速冷却工艺):认为一喷涂完即迅速固化降至室温.
这4种模式可以表征各种叠层制备工艺中产生的降温梯度特征,降温梯度从零到最大,具有典型性,以下算例将以这4种降温梯度分别计算.实际降温梯度应以测量值为准.
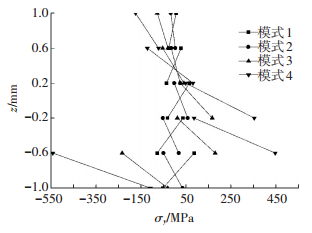
由式(20) 和(22) 得:表 2和表 3分别为制备顺序1和顺序2时4种模式下工件因弯曲变形产生的曲率和最大挠度.由于考虑了制备过程中逐层降温形成的温度梯度,弯曲变形非常显著.
| 表 2 4种模式时曲率和最大挠度(顺序1) Table 2 Curvatures and maximum deflections by 4 cooling models (Order 1) |
| 表 3 4种模式时曲率和最大挠度(顺序2) Table 3 Curvatures and maximum deflections by 4 cooling models (Order 2) |
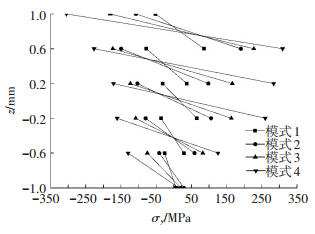
由式(21) 得:图 4和图 5分别为制备顺序1和顺序2时4种模式下沿板厚分布的应力σy.制备顺序不同,各层热残余应力和变形差异大.因此,对于多层材料,存在优化制备顺序问题.
|
图 4 不同模式下热残余应力σy沿厚度的分布(顺序1) Figure 4 Thermal residual stresses distributions through-thickness by different cooling models (Order 1) |
|
图 5 不同模式下热残余应力σy沿厚度的分布(顺序2) Figure 5 Thermal residual stresses distributions through-thickness by different cooling models (Order 2) |
前述结果表明,按照这4种模式的顺序,热残余应力和弯曲挠度依次增大.即降温梯度越大,热残余现象越严重.每种模式的最大应力都发生在弹性模量和热膨胀系数最大的层.在4种模式中,保温制备工艺可有效避免热残余现象,而快速冷却工艺热残余现象最严重.实践中可根据具体的叠层制备工艺来测定降温梯度和模式.
需要说明的是,模式1(同步降温假设)是传统的方法[7],也是本文梯度降温假设的退化结果(退化条件:取降温梯度为0).表 2、表 3、图 4、图 5都给出了不同梯度(模式2、3、4) 与退化结果(模式1) 的值,表明随着梯度减小,与退化结果越趋近,反之增大,符合实际结果.
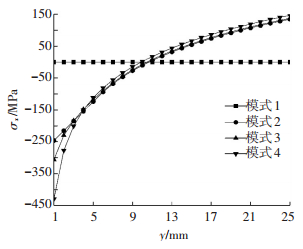
再进行每层平面内的热残余分析.平面内的热残余问题视具体叠层制备工艺而定.如果是由片状材料逐次叠层的,同一层平面内无温差,不出现平面内热残余应力σx;如果是逐行扫描(如烧结、喷涂等),则平面内因扫描先后亦存在降温梯度.就该例而言,设每行扫描宽度为2 mm,每层需扫描25次.仍考虑上述4种降温模式(将每层降温模式改为每行降温模式),由式(7) 得第5层的平面应力σx沿工件长度的分布(图 6).与弯曲应力σy一样,按照这4种降温梯度模式的顺序,热残余应力依次增大.即降温梯度越大,热残余现象越严重.第一种模式(保温制备)热残余应力为零,其他降温模式的最大应力都发生在最先扫描的第1行,两端的残余应力相对较大,中间的残余应力较小.
|
图 6 第5层的平面应力σx沿工件长度的分布 Figure 6 Plane stress σx distributions along length in the fifth layer |
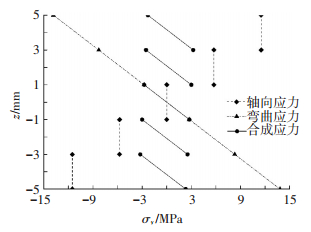
以聚苯乙烯粉末激光烧结快速成型[16]为例,杨氏模量3.6 GPa,拉伸强度60 MPa,热膨胀系数8×10-5/K.制备长度为150 mm,厚度为10 mm,工件分5层烧结,烧结温度为110 ℃,室温为10 ℃.采均等梯度降温假设,每一层的降温梯度取20 ℃.只考察叠层方向的热残余应力σy,沿厚度分布见图 7.
|
图 7 梯度为20 ℃时热残余应力σy沿厚度分布 Figure 7 Thermal residual stress σy distributions through-thickness with 20 ℃ gradient |
图 7中分别给出了轴向拉伸应力σyN(式(14))、弯曲应力σyM(式(15))及合成的总热残余应力σy(式(21)).此例表明:
1) 由于考虑到制备过程中逐层降温形成的温度梯度,同一种材料叠层制备也会出现可观的热残余现象;
2) 从合成的热残余应力σy来看,若仅考虑轴向变形和应力σyN(式(14)),外层的轴向应力最大,中间层最小;当考虑弯曲变形和应力σyM(式(15))后,合成的应力会大幅度减小,且每层应力趋近,呈现反向线性分布.由此可知,弯曲变形实际上是工件降低热残余应力的自动调节机制,以增大弯曲变形为代价来降低残余应力.
5 结论1) 相较于同步降温假设,本文基于梯度降温的热残余分析更贴近实际制备工艺,从而更深入揭示了热残余的成因.
2) 同时考虑了成形过程中沿长度和厚度方向形成的温度梯度,分别建立在层平面和厚度方向引起的热残余变形和应力的解析解,为优化制备工艺提供了更精确可靠的定量分析方法.
3) 根据不同的叠层制备工艺,降温梯度被概括为4种模式:同步降温、均等梯度降温、非均等梯度降温、瞬态降温模式.按照这4种模式的顺序,降温梯度越大,热残余现象越严重.保温制备工艺可有效降低热残余现象,而快速冷却工艺的热残余现象最严重.
4) 弯曲变形实际上是工件降低残余应力的调节机制,通过增大弯曲变形为代价来降低残余应力.
5) 基于梯度降温假设,理论上很好地解释了两种现象:同一种材料叠层制备时也会因降温梯度而产生明显的弯曲变形和残余应力;多种材料叠层制备时制备顺序会显著影响热残余的程度,有必要优化制备顺序.
| [1] |
李素丽, 魏正英, 杜军, 等. 基于金属3D打印技术成形嵌套零件工艺研究[J]. 材料科学与工艺, 2016, 24(6): 1–7.
LI Suli, WEI Zhengying, DU Jun, et al. Research of 3D printing technology based on metal double nozzle to form the hanging parts[J]. Materials Science and Technology, 2016, 24(6): 1–7. DOI: 10.11951/j.issn.1005-0299.20160601 |
| [2] | YU Q M, CEN L. Residual stress distribution along interfaces in thermal barrier coating system under thermal cycles[J]. Ceramics International, 2017, 43(3): 3089–3100. DOI: 10.1016/j.ceramint.2016.11.119 |
| [3] | DECKER S, KRVGER L. Mechanical properties of a CrMnNi steel/Mg-PSZ-FGM processed by asymmetric spark plasma sintering[J]. Materials & Design, 2017, 115: 8–16. |
| [4] | LI J, ZANG Y, WANG W. Elastic modulus and stress analysis of porous titanium parts fabricated by selective laser melting[J]. Journal of Harbin Institute of Technology, 2016, 23(2): 46–50. |
| [5] | SUHIR E. Stresses in Bi-metal thermostats[J]. Journal of Applied Mechanics, 1986, 53(3): 657–660. DOI: 10.1115/1.3171827 |
| [6] | TOWNSEND P H, BARNETT D M. Elastic relationships in layered composite media with approximation for the case of thin films on a thick substrate[J]. Journal of Applied Physics, 1987, 62(11): 4438–4444. DOI: 10.1063/1.339082 |
| [7] | ZHANG X C, XU B S, WANG H D, et al. An analytical model for predicting thermal residual stresses in multilayer coating systems[J]. Thin Solid Films, 2005, 488(1-2): 274–282. DOI: 10.1016/j.tsf.2005.04.027 |
| [8] | ZHANG X C, XU B S, WANG H D, et al. Modeling of the residual stresses in plasma-spraying functionally graded ZrO2/NiCoCrAlY coatings using finite element method[J]. Materials and Design, 2006, 27(4): 308–315. DOI: 10.1016/j.matdes.2004.10.026 |
| [9] |
舒小平. 功能梯度涂层壳体热残余应力分析[J]. 机械科学与技术, 2010, 29(10): 1370–1375.
SHU Xiaoping. Thermal residual stresses of shells with functionally graded coatings[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(10): 1370–1375. |
| [10] | WANG L, WANG Y, SUN X G, et al. Finite element simulation of residual stress of double-ceramic-layer La2Zr2O7/8YSZ thermal barrier coatings using birth and death element technique[J]. Computational Materials Science, 2012, 53: 117–127. DOI: 10.1016/j.commatsci.2011.09.028 |
| [11] | SLÁMEČKA K, SKALKA P, POKLUDA J, et al. Finite element simulation of stresses in a plasma-sprayed thermal barrier coating with an irregular top-coat/bond-coat interface[J]. Surface and Coating Technology, 2016, 304: 574–583. DOI: 10.1016/j.surfcoat.2016.07.066 |
| [12] |
龚京风, 宣领宽, 周少伟, 等. 热障涂层活塞热应力分析的格点型有限体积法[J]. 哈尔滨工业大学学报, 2016, 48(7): 76–81.
GONG Jingfeng, XUAN Lingkuan, ZHOU Shaowei, et al. Cell vertex FVM for thermoelastic analysis of the piston with thermal barrier coating[J]. Journal of Harbin Institute of Technology, 2016, 48(7): 76–81. |
| [13] |
王维, 王兴良, 佟明, 等. 选择性激光烧结快速成形制件翘曲变形的研究[J]. 铸造技术, 2010, 31(4): 507–510.
WANG Wei, WANG Xingliang, TONG Ming, et al. Warping distortion defect of selective laser sintering rapid prototyping work pieces[J]. Foundry Technology, 2010, 31(4): 507–510. |
| [14] |
闫旭日, 颜永年, 张人佶, 等. 分层实体制造中层间应力和翘曲变形的研究[J]. 机械工程学报, 2003, 39(5): 36–40.
YAN Xuri, YAN Yongnian, ZHANG Renji, et al. Study on the interlaminar stress and warpage in laminated object manufacturing[J]. Chinese Journal of Mechanical Engineering, 2003, 39(5): 36–40. |
| [15] |
王天明, 习俊通, 金烨. 熔融堆积成形中的原型翘曲变形[J]. 机械工程学报, 2006, 42(3): 233–238.
WANG Tianming, XI Juntong, JIN Ye. Prototype warp deformation in the FDM process[J]. Chinese Journal of Mechanical Engineering, 2006, 42(3): 233–238. |
| [16] |
舒小平. 叠层制备热应力分析[M]. 南京: 南京大学出版社, 2015.
SHU Xiaoping. Thermal stresses on laminated object manufacturing[M]. Nanjing: Nanjing University Press, 2015. |
 2017, Vol. 25
2017, Vol. 25


