微波是指频率为300 MHz至3 000 GHz范围内的电磁波.微波技术发展迅速,并已得到广泛应用.其中,微波加热是微波应用的一个重要组成部分,它是通过将材料所吸收的微波能转化为自身内部的动能和热能的过程,与常规烧结方式相比,微波加热过程是一种电磁场能量在传输过程中损耗的过程,具有加热均匀、烧结温度低、烧结时间短、能源利用率和加热效率高(比常规烧结节省80%左右)、安全无污染等优点[1-4].
近几年,动力锂离子电池的发展迅猛[5],其中,锂离子动力电池正极材料包括磷酸铁锂(LiFePO4)、锰酸锂(LiMn2O4)、镍钴锰三元材料(LiNi1-x-yCoxMnyO2)3种[6].目前,动力锂离子电池正极材料主要的合成方法有高温固相法、共沉淀法、溶胶凝胶法、喷雾热分解法和湿化学法等[7-12].其中,高温固相法具有操作简单、投入成本低、可以精确控制原料计量比等优点,成为最适宜于大批量工业生产的使用方法.高温固相法虽然工艺简单,但其原料混合均匀程度有限,需要在高温下反应较长时间,合成的产物通常颗粒大小不均匀、晶粒形状不规则、晶界尺寸较大以及电化学性能不容易控制等[13-15].微波法通过改变加热方式改进工艺和提高效率制备LiCo1/3Ni1/3Mn1/3O2,为此,本文将针对微波烧结LiCo1/3Ni1/3Mn1/3O2过程进行进一步的理论分析和实验探讨.
本文借助有限元求解器COMSOL Multi-physics实现了微波电场和热传递的耦合计算,研究并展示了多模腔微波烧结过程的三维模拟结果,并采用数值计算方法计算出理论相对介电常数,并与模拟结果相对照,研究了微波烧结LiCo1/3Ni1/3Mn1/3O2时材料的相对介电常数的变化规律.
1 微波烧结LiCo1/3Ni1/3Mn1/3O2模型建立 1.1 数学模型借助COMSOL Multi-physics对微波烧结LiCo1/3Ni1/3Mn1/3O2进行数值模拟,加热腔内的电场分布通过式(1)求取[16].
| $\nabla \times \left( {\frac{1}{{\mu '}}\nabla \times \vec E} \right) - \frac{{{\omega ^2}}}{c}\left( {\varepsilon ' - i\varepsilon ''} \right)\vec E = 0.$ | (1) |
式中:∇表示散度;
计算材料在电磁场中生成的电阻热即微波加热过程中的损耗功率(P)为
| $P = \frac{1}{2}\left[ {\left( {{\sigma _{EC}} + \omega \varepsilon ''} \right){E^2} + \omega {{\mu ''}_{\rm{r}}}{H^2}} \right].$ | (2) |
式中:H为磁场强度;σEC为电导率;μ″r为被加热物质的磁损耗因子(相对磁导率的虚部).由于可以忽略磁效应的作用,故式(2)右端第二项在求解中可被消除.微波烧结的有限元模型中,在理想边界条件下,热传导方程为
| $\rho {C_p}\frac{{\partial T}}{{\partial t}} = k{\nabla ^2}T + P$ | (3) |
式中:ρ为密度;Cp为常压热容;k是热传导系数;T为温度;t为时间.
1.2 COMSOL模型的建立由于实验中使用的微波炉是家用矩形波炉,时间温度属于可控因素,但在加热过程中物料受热是否均匀,物料对微波场分布的影响,需要通过模拟进行研究和探讨.
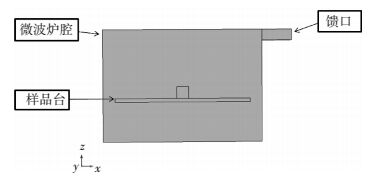
微波炉尺寸为267 mm×270 mm×188 mm.馈口位于z=170 mm的平面上,上表面与微波炉上底同面,其尺寸为50 mm×78 mm×18 mm.将微波炉内腔作为金属面,输入2.45 GHz,功率500 W的矩形TE10平面波.炉腔和波导都是完美的导体,用边界条件n×E=0(n为垂直于边界平面的单位矢量;E为电场强度矢量)表示.利用对称性截取一半模型,由于电场关于对称面镜像对称,因此,对称面可看成是完美的磁导体,用边界条件n×H=0(H为磁场强度矢量)表示.建立的微波炉几何模型如图 1所示.
|
图 1 微波炉的几何模型 Figure 1 The geometric model of microwave oven |
微波恒定功率设置为800 W,初始温度T0=298 K,模拟使用的LiCo1/3Ni1/3Mn1/3O2粉末的初始物理参数一部分是真实测得:由成都志扬微波科技有限公司使用圆柱腔微扰法复介电常数测试得相对介电常数ε=6.3,由排水法测得密度ρ=4 678 kg/m3,一部分根据文献得到:电导率σ=1.13 S/m,相对磁导率μ′=1,热传导率k=1.5 W/(m·K),等压热容Cp=800 J/(kg·K).需要着重说明以下3点:1)LiCo1/3Ni1/3Mn1/3O2材料作为一种粉末状材料,其相对介电常数、电导率等电介质参数,目前仍是材料领域需要研究的课题;2)因为微波烧结的致密作用,故测得的相对介电常数是以空气作为填充物;3)从不同文献查阅的相关数据出入很大.因此,上述部分参数设置为初始参数,作常量处理.而作为初步对电磁场和温度场分布的研究,数据基本可靠,在后续的研究中将进一步获得更真实准确的材料参数.
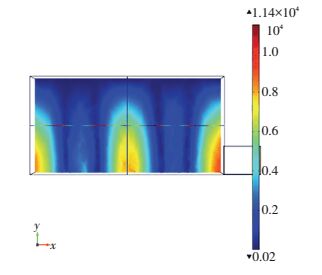
2 仿真结果与分析 2.1 空腔中微波场的分布通过以上设定,在COMSOL Multi-physics求解器中获得结果,空腔中微波场的分布如图 2所示.在微波炉的z=94 mm横截面,如图 2所示,微波在炉腔内传播遇到金属腔体发生全发射,从而叠加产生驻波.通过分析微波炉的谐振方式以及电磁场的分布,找出合适的样品放置位置.因此,样品台设置在高度为z=94 mm的平面.其中电场的最大值E=11 400 V/m.
|
图 2 空腔中电磁场的分布 Figure 2 Electromagnetic field in the non-loaded microwave oven |
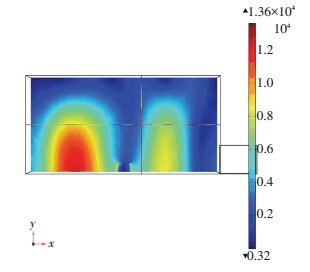
在微波场中放置样品后,样品被设为边长为0.02 m的正方体,由于样品的吸波性能,炉腔内电磁场的分布将会受到影响,如图 3所示.放入样品后,对比图 2和图 3可知,样品周围微波场明显减弱.说明在有较大负载时,微波炉内部表面的电场强度减弱,这有助于微波的吸收,但其他位置的电场却有所增强,电场强度的最大值为E=13 600 V/m.
|
图 3 电磁场分布 Figure 3 Electromagnetic field distribution |
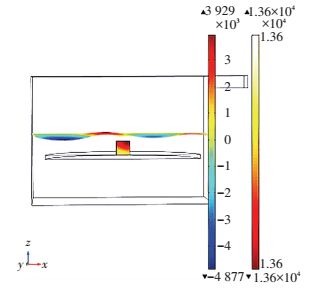
如图 4所示,样品的各部分加热并不均匀,在实际烧结过程中,可以采取样品台旋转等方式解决这一问题.此外,微波烧结正极材料时,温度场的分布取决于两个方面,一方面是材料密度的分布情况,另一个方面是电磁场的分布.但在模拟过程中,默认材料的密度均匀,因此,在电磁场固定不变的前提下,模拟所得结果,温度场的分布同样适合其他正极材料.
|
图 4 温度场分布 Figure 4 Temperature field distribution |
表 1为由成都志扬微波科技有限公司使用圆柱腔微扰法复介电常数测试测得的LiCo1/3Ni1/3Mn1/3O2在2.45 GHz下烧结得到的不同温度(θ)时的复合介电常数(ε),以及模拟得到的不同温度下吸收的微波功率(P).
| 表 1 LiCo1/3Ni1/3Mn1/3O2在不同温度下的复合介电常数和微波吸收功率 Table 1 The compound dielectric and microwave absorption power of the LiCo1/3Ni1/3Mn1/3O2 at different temperature |
通过模拟所得到的数据,可以求解样品的相对介电常数.微波吸收功率为[17]
| $P = 2{\rm{ \mathit{ π} }}f{E^2}{\varepsilon _0}\varepsilon {\prime _{\rm{r}}}V{\rm{tan}}\delta .$ | (4) |
式中:P为吸收的功率;f是微波频率;E是电场强度;V是有效体积;tan δ为损耗角正切;εo是真空介电常数;ε′r是材料的相对介电常数.
由于实验所得的相对介电常数是以空气作为填充物,故LiCo1/3Ni1/3Mn1/3O2材料的相对介电常数可以由李赫德涅凯法则计算[18].
| $_{\rm{}}{\rm{In}}\varepsilon = {\rm{In}}{\varepsilon _2} + ({\rm{In}}{\varepsilon _1} - {\rm{In}}{\varepsilon _2}){v_1}.$ | (5) |
式中:ε为混合物材料样品的介电常数;ε1为已知电磁特性材料的介电常数(此处即为空气的相对介电常数);v1为其在混合物中的体积分数,ε2为待测粉末材料的介电常数.
有效体积和体积分数均通过测试来自在不同温度样品的密度计算所得.其中,f=2.45×109 Hz,根据样品周围电场分布情况,求得平均电场约为2 500 V/M,εo=8.85×10-12 F/m,ε1=1,tan δ=0.054.带入式(4)可求LiCo1/3Ni1/3Mn1/3O2的相对介电常数,并将实验测得的复合介电常数带入式(5)计算得到物料的相对介电常数,计算结果如表 2所示,其中,ε′1是由实验数据计算所得相对介电常数,ε′2是由模拟计算所得相对介电常数.
| 表 2 实验和模拟所得相对介电常数 Table 2 Relative permittivity obtained by experiments and simulation |
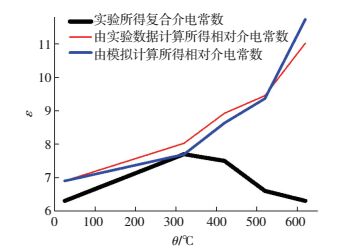
将表 2所得数据绘制成曲线如图 5所示,可以看到,当温度上升到320~420 ℃某个临界点时,实验所得复合介电常数由开始的上升变化为下降,这是因为在烧结粉末过程中,由于致密化的作用[19],吸收微波的有效体积在不断变小;而通过李赫德涅凯法则计算后,所得LiCo1/3Ni1/3Mn1/3O2始终在变大,与模拟结果趋势相同,但数据上大小有所不同,这是因为烧结模型采用LiCo1/3Ni1/3Mn1/3O2物理参数并非全是准确数值,因此,模拟仿真得到的相对介电常数和变化规律只具有参照意义.
|
图 5 实验和模拟所得相对介电常数(ε)随温度(θ)变化曲线 Figure 5 Relative permittivity obtained by experiments and simulation as a function of temperature |
1) 使用COMSOL Multi-physics建立的模型,有效地仿真了矩形微波炉内电磁场的分布情况,且有效模拟了烧结过程中LiCo1/3Ni1/3Mn1/3O2样品内部温度场的分布情况.
2) 烧结LiCo1/3Ni1/3Mn1/3O2过程中,存在有空气填充物时,复合介电常数先增大后减小,而LiCo1/3Ni1/3Mn1/3O2的相对介电常数在720 ℃以下,随着温度的上升而增大.
| [1] |
梁宝岩, 张旺玺, 王艳芝, 等. 微波烧结制备Ti3SiC2-金刚石复合材料的显微形貌及界面反应机理[J]. 硅酸盐通报, 2016, 35(3): 725–731.
LIANG Baoyan, ZHANG Wangxi, WANG Yanzhi, et al. Microstructure and interfacial reaction mechanism of Ti3SiC2-diamond composites fabricated by microwave sintering[J]. Bulletin of the Chinese Ceramic Society, 2016, 35(3): 725–731. DOI: 10.13208/j.electrochem.151128 |
| [2] | SCHWENKE A M, HOEPPENER S, SCHUBERT U S. Synthesis and modification of carbon nanomaterials utilizing microwave heating[J]. Advanced Materials, 2015, 27(28): 4113–4141. DOI: 10.1002/adma.201500472 |
| [3] |
张家敏, 易健宏, 甘国友. 微波烧结Mn-Zn铁氧体的微观结构演变特征[J]. Materials Science & Technology, 2014, 2: 17–23.
ZHANG Jiamin, YI Jianhong, GAN Guoyou. Microstructure characteristics of microwave sintered Mn-Zn ferrite soft magnetic materials[J]. Materials Science and Technology, 2014, 2: 17–23. |
| [4] | XIONG G, NIE Y, JI D, et al. Characterization of biomedical hydroxyapatite/magnesium composites prepared by powder metallurgy assisted with microwave sintering[J]. Current Applied Physics, 2016, 16(8): 830–836. DOI: 10.1016/j.cap.2016.05.004 |
| [5] |
蒋志军, 张亚莉, 王乾, 等. 三元正极材料前驱体Ni1/3Co1/3Mn1/3(OH)2的连续合成与条件探究[J]. 电化学, 2016, 5: 528–533.
JIANG Zhijun, ZHANG Yali, WANG Qian, et al. Continuous synthesis and condition exploration of precursor Ni1/3Co1/3Mn1/3(OH)2 of ternary cathode material[J]. Electrochemistry, 2016, 5: 528–533. DOI: 10.13208/j.electrochem.151128 |
| [6] |
谭聪, 朱文, 刘勇, 等. 锂离子动力电池正极材料的研究进展[J]. 材料导报, 2011, 25: 291–296.
TAN Cong, ZHU Wen, LIU Yong, et al. Progress in lithium power ion battery cathode materials[J]. Materials Review, 2011, 25: 291–296. |
| [7] |
夏书标, 张英杰, 董鹏, 等. 固相法制备锂离子电池正极材料LiNi0.80Co0.15Al0.05O2及其性能研究[J]. 材料科学与工艺, 2014, 22(3): 124–128.
XIA Shubiao, ZHANG Yingjie, DONG Peng, et al. Synthesis and properties of LiNi0.80Co0.15Al0.05O2 cathode material for Liion batteries by solidstate method[J]. Materials Science and Technology, 2014, 22(3): 124–128. DOI: 10.11951/j.issn.1005-0299.20140322 |
| [8] | GOU J, JIAO L, YUAN H, et al. Effect of synthesis condition on the structural and electrochemical properties of Li[Ni1/3Mn1/3Co1/3]O2 prepared by the metal acetates decomposition method[J]. Electrochimica Acta, 2006, 51: 3731–3735. DOI: 10.1016/j.electacta.2005.10.037 |
| [9] | YASUHIRO F, HIROSHI M, NAOTO SI, et al. Structural and electrochemical properties of LiNi1/3Co1/3Mn1/3O2: Calcination temperature dependence[J]. J Power Sources, 2007, 171(2): 894–903. DOI: 10.1016/j.jpowsour.2007.06.017 |
| [10] | DY WANG, J XIA, L MA, et al. A systematic study of electrolyte additives in Li[Ni1/3Mn1/3Co1/3]O2 (NMC)/graphite pouch cells[J]. Journal of the Electrochemical Society, 2014, 161(12): A1818–A1827. DOI: 10.1149/2.0511412jes |
| [11] | KIZILTAS-YAVUZ N, HERKLOTZ M, HASHEM A M, et al. Synthesis structural magnetic and electrochemical properties of LiNi1/3Mn1/3Co1/3O2 prepared by a solgel method using table sugar as chelating agent[J]. Electrochimica Acta, 2013, 113: 313–321. DOI: 10.1016/j.electacta.2013.09.065 |
| [12] | ZHENG H, TAN L, LIU G, et al. Calendering effects on the physical and electrochemical properties of Li[Ni1/3Mn1/3Co1/3]O2 cathode[J]. Journal of Power Sources, 2012, 208: 52–57. DOI: 10.1016/j.jpowsour.2012.02.001 |
| [13] | WU S L, ZHANG W, Song X, et al. High rate capability of Li(Ni1/3Mn1/3Co1/3)O2 electrode for Liion batteries[J]. Journal of The Electrochemical Society, 2012, 159(4): A438–A444. DOI: 10.1149/2.062204jes |
| [14] | OZOEMENA K. Insights into microwave-enhanced cycling performance of nickel-doped LiMn2O4 spinel Cathode Material at Elevated Temperature[C]//18th International Meeting on Lithium Batteries (June 19-24, 2016). Ecs, 2016. |
| [15] | SHI S, ZHANG S, WU Z, et al. Full microwave synthesis of advanced Li-rich manganese based cathode material for lithium ion batteries[J]. Journal of Power Sources, 2017, 337: 82–91. DOI: 10.1016/j.jpowsour.2016.10.107 |
| [16] | SALVI D, BOLDOR D, AITA G M, et al. Comsol multiphysics model for continuous flow microwave heating of liquids[J]. Journal of food engineering, 2011, 104(3): 422–429. DOI: 10.1016/j.jfoodeng.2011.01.005 |
| [17] |
金钦汉. 微波化学[M]. 第一版. 北京: 科学出版社, 1999: 42.
JIN Qinhan. Microwave chemistry[M]. First Edition. Beijing: Science Press, 1999: 42. |
| [18] | SIMPKIN R. Derivation of Lichtenecker′s logarithmic mixture formula from Maxwell′s equations[J]. IEEE Transactions on Microwave Theory and Techniques, 2010, 58(3): 545–550. DOI: 10.1109/TMTT.2010.2040406 |
| [19] | LUO S D, YI J H, GUO Y L, et al. Microwave sintering W-Cu composites: analyses of densification and microstructural homogenization[J]. Journal of Alloys and Compounds, 2009, 473(1): L5–L9. DOI: 10.1016/j.jallcom.2008.05.038 |
 2017, Vol. 25
2017, Vol. 25


