2. 中航工业沈阳飞机工业(集团)有限责任公司,沈阳 110034
2. AVIC Shenyang Aircraft Industrial(Group)Co., Ltd., Shenyang 110034, China
在飞机钣金制造过程中,框肋类零件形状复杂,种类多,且批量小,采用传统的制造方法无法满足航空工厂的要求.橡皮成形工艺是利用橡皮作为弹性凹模(或凸模),用液体作为传压介质使金属板料随刚性凸模(或凹模)变形的一种软模成形方法[1].与传统制造方法相比,橡皮成形工艺可成形复杂形状零件,提高零件成形质量和结构的可靠性,工人劳动强度低,大大缩短了生产准备周期,在现代飞机制造中占50%以上.
起皱是板料在成形过程中受压失稳的一个主要表现形式[2].起皱的形成可由Hill的分叉准则来预测,即假设一个局部的分歧位移区,忽略接触条件和连续性条件,推导出材料性能和几何性质的临界应力,但预测结果往往不准确,导致成形时产生起皱现象.对于起皱的控制已经成为橡皮成形至关重要的一部分,航空工厂常采用侧压块来消皱[3].随着有限元模拟技术的进一步成熟,通过数值模拟可以对成形零件产生的缺陷进行预示[4-5],从而提高工艺设计的效率.
目前,国内外学者对橡皮成形过程中起皱做了大量的研究.Neto等[6]通过数值模拟认为,增大摩擦有利于降低起皱的可能;Kim等[7]提出起皱因子概念,通过模拟成形过程中起皱因子来预测起皱的位置和相对可能性;刘垒等[8]对角压条进行模拟,预测了钣金件成形过程中的缺陷并分析了缺陷产生的原因;孙永娜等[9]通过对钛合金零件边缘的皱纹波长和峰高的定量研究来预测起皱;王福东[10]通过对大曲率凸弯边零件进行模拟,分析了侧压块各参数对成形结果的影响.但少有人对侧压块各几何参数进行优化模拟研究.
本文采用Abaqus非线性有限元分析软件对带侧压块典型零件进行数值模拟,以最大增厚率作为评价指标,通过正交实验选择影响最大的几何参数作为响应面建模的变量,建立变量与指标之间的响应面关系,并用遗传算法对侧压块参数进行优化.
1 试验 1.1 材料拉伸试验 1.1.1 试验方案制定新淬火态铝合金是热处理的中间状态,具有塑性好、硬度低、易成形等优点,在材料手册中没有提供可供参考的成形性能指标参数,更没有不同时效时间的性能参数[11-12].通过对新淬火状态下的铝合金的成形性能指标参数试验,可以为橡皮成形有限元仿真提供可靠的参考依据.
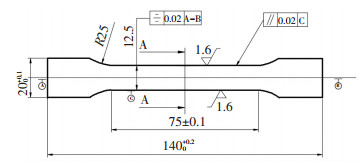
根据GB/T 228.1—2010《金属材料拉伸试验第一部分:室温试验方法》相关要求,设计如图 1所示的试件.
|
图 1 单向拉伸试件 Figure 1 Uniaxial tensile specimen |
由于铝合金板料固溶处理后组织变化极其不稳定,易发生加工硬化,因此需要安排合理的时效时间,见表 1.
| 表 1 时效时间表 Table 1 Aging schedule |
由于铝合金板料在淬火之后会引起局部的变形翘曲,造成拉伸试验测得的材料数据不准确,因此淬火之后必须进行板料校形,校平3次后放入低温试验箱中,并保证温度波动在±2 ℃.淬火之后校形的过程以及放入到低温试验箱的时间要在10 min内完成.
采用CTM2050微机伺服控制电子万能试验机进行试验,试验机通过伺服电机驱动系统传动横梁上下移动来实现对试件施加载荷,并保证尺寸精度控制在±0.3%.将不同板料轧制方向和不同时效时间的试件夹持到试验机上,连接电子传感器进行试验,试件的变形量由系统实时记录.
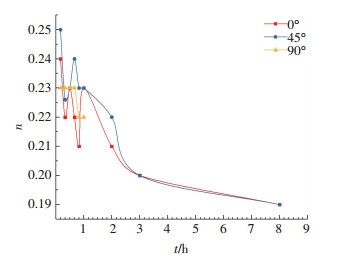
1.1.2 试验结果数据分析硬化指数n曲线如图 2所示,n值的总体趋势是随着时效时间的增长而减少,当达到节点60 min时,下降幅度增大. n对板料的成形性能及质量有较大的影响,n值越大,成形极限越高.
|
图 2 硬化指数n曲线 Figure 2 Hardening index n curve |
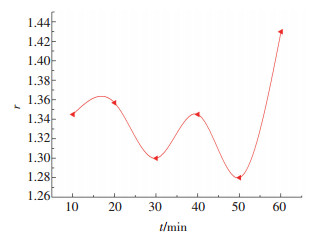
通过计算得到厚向异性指数r曲线如图 3所示,当时效时间小于60 min时,新淬火状态下的铝合金r值有增有减,但整体呈增长的趋势.板料的r值越大,有利于凸缘的切向收缩变形,降低了起皱的可能性.
|
图 3 厚向异性指数r曲线 Figure 3 Thickness direction anisotropic index r curve |
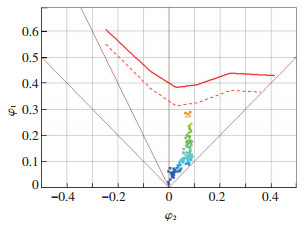
在试验过程中,采用刚性凸模对试件进行胀形试验,将一侧表面印有方形网格的试件置于模具与圧边圈之间,利用压边力压紧拉延筋以外的材料,试件中部在凸模的作用下产生变形并凸起,当凸起部分某个局部产生颈缩或者破裂时试验停止,得到材料的FLD如图 4所示.
|
图 4 LY12M材料的FLD图 Figure 4 FLD diagram of LY12M materials |
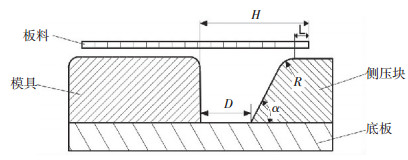
采用侧压块成形时,其防皱原理如图 5所示.侧压块主要工艺参数有:搭边长度L、侧压块与模具之间的距离D、侧压块倾角α、侧压块圆角半径R.由于板料与侧压块之间存在摩擦,板料在成形的过程中受到侧压块的附加拉应力.根据Tresca屈服准则,屈服应力σs=σr-σθ其中σr为径向拉应力,σθ为切向压应力,增加σr可以减小σθ,从而起到防皱的作用.搭边长度L不宜过长,如果摩擦力过大,板料会有拉裂的危险.
|
图 5 侧压块主要几何参数 Figure 5 The main geometric parameters of side blank holder |
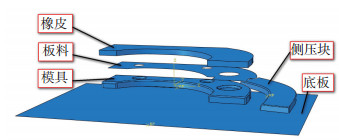
在CATIA中设计出模具、侧压块、板料、底板和橡皮,为了简化计算,提高计算效率,模具、侧压块、板料、底板均采用片体来表示,将模具、侧压块、板料、底板和橡皮以stp的形式导入Abaqus软件,建立的有限元原始模型如图 6所示.
|
图 6 橡皮成形有限元模型 Figure 6 The finite element model of rubber forming |
在Abaqus中,将板料定义为弹塑性可变形体,橡皮定义为超弹塑性体,模具、侧压块和底板定义为刚体.橡皮采用8节点六面体扫略网格,板料采用S4R四边形缩减积分自由网格,模具、侧压块、底板采用四边形刚体自由网格,网格全局总体种子均为4.板料为铝合金LY12M,厚度为1.2 mm,主要参数见表 2.橡皮材料采用Mooney-Rivlin模型,摩擦因子均为0.2[10],压力加载方式为Smooth,加载时间为10 ms,成形压力为50 MPa.
| 表 2 LY12M铝合金参数 Table 2 Parameters of LY12M aluminum alloy |
由上述侧压块几何参数可知,主要有4个设计变量和1个起皱评价指标.为了得到侧压块几何参数对起皱的影响规律,以弯边高度H=20 mm时,采用4因素3水平正交试验进行模拟,正交试验方案和结果见表 3,对正交结果进行极差分析见表 3.
| 表 3 正交试验方案及结果 Table 3 The orthogonal experiment scheme and results |
表 4为正交试验结果极差分析.由表 4可知,不同影响因素的影响程度不同,需要综合考虑各因素的影响程度,最终得出较优的组合.
| 表 4 正交试验结果极差分析 Table 4 Range analysis of orthogonal experiment results |
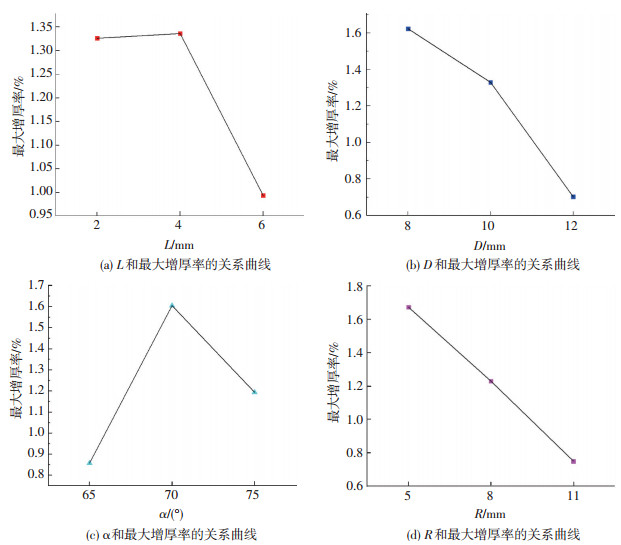
|
图 7 各因素与指标趋势图 Figure 7 The factors and the index trend chart:(a) L and the maximum thickening rate curve; (b) D and the maximum thickening rate curve; (c) α and the maximum thickening rate curve; (d) R and the maximum thickening rate curve |
搭边长度L对最大增厚率的影响相对其他3个参数比较小,因此对本文对侧压块的参数D、α、R进行优化,L取6 mm.
3.2 响应面建模 3.2.1 响应面建模数据的提取均匀设计是由方开泰和王元两位数学家于1978年创立的试验设计方法,该方法认为, 试验点在设计空间均匀分散,能代表整个设计空间的主要特性[13-14].对于条件范围变化大且需要对水平试验的情况,能极大降低试验次数.
本文利用均匀试验设计方法对H=20 mm虚拟设计出10组试验进行模拟,获得响应面建模的数据见表 5.
| 表 5 均匀试验设计的参数水平设置 Table 5 Setting of the parameters of the uniform experimental design level |
响应面法是通过近似构造一个具有明确表达形式的函数,对响应受多个因素影响的问题进行建模和分析,最终达到优化响应值的目的.
本文针对H=14、16、18和20 mm的情况,对D、α、R和最大增厚率利用多项式建立响应面关系,各多项式的系数见表 6~8.
| 表 6 一次多项式系数 Table 6 Linear polynomial coefficients |
| 表 7 二次多项式系数 Table 7 Quadratic polynomial coefficients |
| 表 8 三次多项式系数 Table 8 Cubic polynomial coefficients |
1) 一次多项式:
| $ f\left( x \right) = {a_0} + {a_1}{x_1} + {a_2}{x_2} + {a_3}{x_3}. $ | (1) |
2) 二次多项式:
| $ \begin{array}{l} f\left( x \right) = {a_0} + {a_1}{x_1} + {a_2}{x_2} + {a_3}{x_3} + {a_{11}}x_1^2 + {a_{12}}{x_1}{x_2} + \\ {a_{13}}{x_1}{x_3} + {a_{22}}x_2^2 + {a_{23}}{x_2}{x_3} + {a_{33}}x_3^2. \end{array} $ | (2) |
3) 三次多项式:
| $ \begin{array}{l} f\left( x \right) = {a_0} + {a_1}{x_1} + {a_2}{x_2} + {a_3}{x_3} + {a_{11}}x_1^2 + {a_{12}}{x_1}{x_2}\\ + {a_{13}}{x_1}{x_3} + {a_{22}}x_2^2 + {a_{23}}{x_2}{x_3} + {a_{33}}x_3^2 + {a_{111}}x_1^3\\ + {a_{123}}{x_1}{x_2}{x_3} + {a_{222}}x_2^3 + {a_{333}}x_3^3. \end{array} $ | (3) |
试验中采用R2作为误差大小的评价标准,其误差结果见表 9.从表 9可以看出,二次多项式效果最好,其响应面如图 8所示.

|
图 8 响应面 Figure 8 The response surface:(a) H=14 mm; (b) H=16 mm; (c) H=18 mm; (d) H=20 mm |
| 表 9 不同弯边高度响应面各多项式函数误差比较 Table 9 Comparison of different functional errors of response surface with different flange height |
遗传算法是以遗传学理论和自然选择为基础,在生物进化过程中整个群体内部染色体和适者生存法则的随机信息交换机制相结合的高效全局多参数寻找最优解的方法[15].建立好优化模型,采用MATLAB的遗传算法工具箱对二次多项式在可行域上计算最优解,其主要分为如下7个步骤.
第1步:对遗传算法的运行参数进行赋值.参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数.
第2步:建立区域描述器.根据模型的求解量的约束条件,设置变量的取值范围.
第3步:在第2步的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值.
第4步:执行比例选择算子进行选择操作.
第5步:按交叉概率对交叉算子执行交叉操作.
第6步:按变异概率执行离散变异操作.
第7步:计算第6步得到局部最优解中每个个体的适应值,并执行最优个体保存策略.
最终计算得到的最优解参数见表 10.
| 表 10 最优解参数 Table 10 The optimal solution parameters |
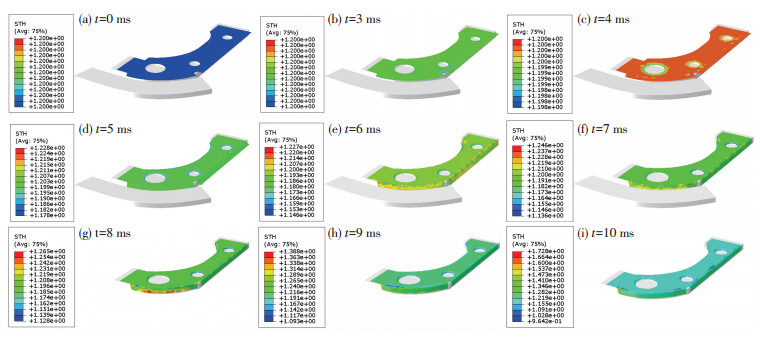
利用Abaqus对优化后的参数进行模拟验证,板料成形过程不同时刻厚度变化情况如图 9所示.
|
图 9 板料成形厚度变化图 Figure 9 Sheet metal forming thickness change graphs: (a) t=0 ms; (b) t=3 ms; (c) t=4 ms; (d) t=5 ms; (e) t=6 ms; (f) t=7 ms; (g) t=8 ms; (h) t=9 ms; (i) t=10 ms |
通过如图 10所示模拟结果的对比可以看出,无侧压块的情况下,凸弯边部分有较为明显的起皱,而在有侧压块的情况下,无起皱现象,为实际成形试验提供了依据.

|
图 10 成形结果 Figure 10 The forming results: (a) without side blank holder; (b) with side blank holder |
通过Abaqus有限元模拟得出的工艺参数以及侧压块外形尺寸设计如图 11所示的模具,模具材料为Q235钢.

|
图 11 模具实物照片 Figure 11 Die pictures |
本次橡皮成形试验采用ABB公司生产的QFC 1.4×4—1000橡皮囊液压机,其工作效率高,使用方便,省时高效.由于板料在成形过程中,使用不同润滑剂会出现不同的摩擦状况,传统的板料成形润滑剂有氯化石蜡、机油等,为使摩擦条件与模拟过程相符合,本次试验选用板料成形专用SDL水基润滑剂,由于化学吸附的选择倾向性,在润滑剂中添加一定量的油酸钠,使微粒均匀分布.成形后的零件如图 12所示.

|
图 12 成形零件照片 Figure 12 Forming parts photos: (a) without side blank holder; (b) with side blank holder; (c) mass production |
从图 12可以看出:在无侧压块的情况下,零件凸弯边边缘部分有较为明显的起皱;而在有侧压块的情况下,板料和模具贴合率相对较高,起皱不明显,得到了预期相应的改善.这是因为板料和侧压块之间的摩擦力相当于压延过程中压边圈所产生的压边力,降低了其切向压应力,限制了板料在凸弯边周向上的收缩,提高了板料的流动稳定性,从而有效控制了起皱程度.
6 结论1) 对新淬火状态下铝合金板料进行单向拉伸及FLD试验,分析成形性能指标,为有限元模拟提供理论依据.
2) 采用数值模拟方法对侧压块各几何参数进行正交模拟,将起皱量化,建立起皱指标与侧压块之间的响应面模型,并优化得到不同弯边高度侧压块参数.
3) 在数值模拟的基础上,成形出合格的钣金零件,验证了侧压块优化方法的可靠性.
| [1] | 李泷杲. 金属板料成形有限元基础:PAMSTAMP2G(Autostamp)[M]. 北京: 北京航空航天大学出版社, 2008: 315-316. |
| [2] | WANG C T, KINZEL G, ALTAN T. Failure and wrinkling criteria and mathematical modeling of shrink and stretch flanging operations in sheet-metal forming[J]. Journal of Materials Processing Technology, 1995, 53(3/4): 759–780. |
| [3] | 航空制造工程手册总编委会. 飞机钣金成形工艺[M]. 北京: 航空工业出版社, 1992. |
| [4] | BROWNE D J, BATTIKHA E. Optimisation of aluminium sheet forming using a flexible die[J]. Journal of Materials Processing Technology, 1995, 55(3/4): 218–223. |
| [5] | ASNAFI N. On stretch and shrink flanging of sheet alu-minium by fluid forming[J]. Journal of Materials Processing Technology, 1999, 96(1/2/3): 198–214. |
| [6] | NETO D M, OLIVEIRA M C, ALVES J L, et al. Prediction of wrinkling and springback in sheet metal forming[C]//NUMIFORM 2016. Troyes: MATEC Web of Conferences, 2016, 80:03005.DOI:https://doi.org/10.1051/matecconf/20168003005. |
| [7] | KIM J B, YANG D Y. Prediction of wrinkling initiation in sheet metal forming processes[J]. Engineering Computations, 2003, 20(1): 6–39. DOI: 10.1108/02644400310458810 |
| [8] |
刘垒, 孙志宏, 庄璐玮, 等. 基于PAM-STAMP2G的钛合金钣金零件橡皮囊成形有限元模拟[J]. 机械制造与自动化, 2016(4): 84–86.
LIU Lei, SUN Zhihong, ZHUANG Luwei, et al. Rubber bladder forming for titanium alloy sheet metal parts based on Pam-Stamp2G finite element simulation[J]. Machine Building & Automation, 2016(4): 84–86. DOI: 10.19344/j.cnki.issn1671-5276.2016.04.025 |
| [9] | SUN Y N, WAN M, WU X D. Wrinkling prediction in rubber forming of Ti-15-3 alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(10): 3002–3010. DOI: 10.1016/S1003-6326(13)62827-7 |
| [10] | 王福东. 大曲率凸弯边零件橡皮囊液压成形工艺研究[D]. 南京: 南京航空航天大学, 2011. |
| [11] |
高宏志, 周贤宾. 新淬火状态硬铝合金板的成形性能及数值模拟[J]. 航空材料学报, 2008, 28(5): 27–31.
GONG Hongzhi, ZHOU Xianbin. Formability and numerical for as-quenched aluminum alloy sheet[J]. Journal of Aeronautical Materials, 2008, 28(5): 27–31. |
| [12] |
高宏志, 周贤宾. 新淬火状态铝合金板的成形极限[J]. 北京航空航天大学学报, 2006, 32(9): 1083–1086.
GONG Hongzhi, ZHOU Xianbin. Forming limits for as-quenched aluminum alloy sheet[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(9): 1083–1086. |
| [13] |
李玉强, 崔振山, 陈军, 等. 基于响应面模型的6σ稳健设计方法[J]. 上海交通大学学报, 2006, 40(2): 201–205.
LI Yuqiang, CUI Zhenshan, CHEN Jun, et al. Six sigma robust design methodology based on response surface model[J]. Journal of Shanghai Jiaotong University, 2006, 40(2): 201–205. |
| [14] |
王淼, 李东升, 李小强, 等. 橡皮液压成形工艺的可靠性稳健优化设计方法[J]. 北京航空航天大学学报, 2012, 38(8): 1064–1069.
WANG Miao, LI Dongsheng, LI Xiaoqiang, et al. Reliability-based robust optimization design for rubber fluid cell forming process[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 1064–1069. |
| [15] | 雷英杰. MATLAB遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2014: 146-207. |
 2018, Vol. 26
2018, Vol. 26


