近年来, 随着人们环境保护及节能减排意识的提高,迫切需要轻质高强度材料,如铝合金、钛合金、镁合金等来替代传统材料以达到零部件结构轻量化的目的[1-3].然而,轻质高强度材料的室温难加工性(塑性低,强度高)是限制其广泛应用的一个主要原因[4-5].针对这一问题,近年来学者们提出一种新颖的电流辅助成形方法,即在发生塑性变形的金属中通入电流,使材料塑性提高、变形抗力下降以及微观组织改善[6].
国内外学者主要从以下几个方面研究了电流对金属材料性能的改善.1)电流提高金属塑性,降低变形抗力.Roh等人[7]在5052-H32铝合金单向拉伸过程中通入周期作用的脉冲电流,研究发现在其研究的电参数范围内,周期脉冲电流作用下的试样在发生颈缩时的延伸率最高增加了320%,且在脉冲电流作用周期内拉伸力显著降低,Roth等[8]在单向拉伸时将周期性脉冲电流通入5754铝合金试样中,在标距范围内获得了接近400%的延伸率.解焕阳等人[9]通过对AZ31B镁合金试样进行等温单向拉伸试验以及脉冲电流辅助拉伸试验,研究了AZ31B镁合金的电致塑性变形行为,证实了流动应力的纯电致塑性效应,通过比较试样的微观组织分析了高温和脉冲电流作用下流动应力减少的机理,结果证实脉冲电流诱导产生的动态再结晶对流动应力的减少及塑性的提升起到重要作用.2)电流抑制成形零件的回弹.Green等[10]在变形后的6111铝合金试件中通入电流后发现,变形件的回弹量明显减少,甚至能够完全消除回弹.而且,解焕阳[11]等人通过电脉冲辅助V弯研究了脉冲电流电参数对AZ31B镁合金板料回弹性的影响,结果表明脉冲电流作用下板料中晶粒的细化和孪晶数量的减少是回弹减少的主要原因.3)电流诱导金属材料的退火及晶粒细化.Conrad等[12]研究了脉冲电流对冷变形金属退火组织的影响,研究表明脉冲电流可以促使材料的再结晶.Maki等提出了一种基于电流焦耳热效应的热处理新技术[13],该方法在6061铝合金板料中直接通入高密度电流,利用材料自身电阻使其在短时间内(2 s内)被迅速加热至相变温度,实现了热处理的目的,而在如此短的时间内,6061铝合金材料内部的晶粒来不及长大,从而达到细晶的目的.因此,可将板料脉冲电流处理作为一种有效的细晶强化热处理工艺.
目前,科研工作者主要研究了电流对金属材料性能的改善,但未能较为深入地分析一些合金在电流辅助拉伸中所出现的DSA现象及电流作用时导致材料应力降低的因素.为此,本文选用Al-Mg-Si系合金6063T4铝合金为研究对象,在自行设计的电流辅助拉伸模具上进行6063T4铝合金脉冲电流辅助拉伸试验,探讨了脉冲电流峰值对6063T4铝合金力学性能的影响,研究了脉冲电流辅助拉伸过程中材料的DSA现象及其机理,分析讨论了脉冲电流作用时应力降产生的原因,并采用扫描电镜及光学显微镜分别观察了试样断口形貌以及试验前后材料的显微组织变化.
1 实验 1.1 实验材料本实验所用材料是厚度为2.2 mm的6063T4铝合金轧制板料,其化学成分如表 1所示.对原始板料进行金相制样,经镶嵌、研磨、抛光后,使用Keller试剂(HF:HCl:HNO3:H2O=2:3:5:190)腐蚀50~60 s,用清水清洗后在MR5000高倍金相显微镜上对其3个相互垂直的材料平面进行显微组织观察.得到的金相显微组织如图 1所示,3个相互垂直的平面内的材料具有相同的显微组织,6063T4铝合金中主要强化相为Mg2Si,经Keller试剂腐蚀后,在显微组织中呈黑色粒状物[14](图 1(b)).沿板料轧制方向利用电火花线切割制得实验所需拉伸试样,试样尺寸如图 2所示.

|
图 1 6063T4板料的显微组织 Figure 1 Microstructure of 6063T4 aluminum alloy sheet:(a) the planes investigated in the microstructural analysis; (b) the microstructure of the three orthogonal planes |
|
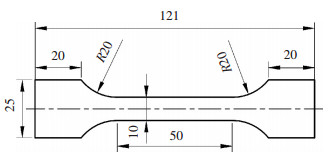
图 2 拉伸试样尺寸(单位:mm) Figure 2 Dimensions of tensile specimen (unit: mm) |
| 表 1 6063T4铝合金板料化学成分(质量分数/%) Table 1 Chemical composition of the 6063T4 aluminum alloy sheet (wt.%) |
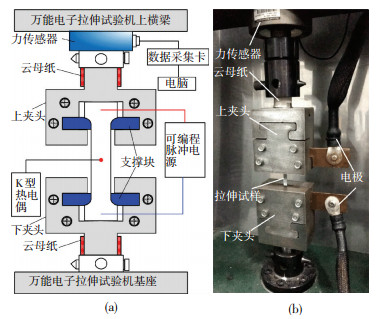
图 3为此脉冲电流辅助拉伸的实验装置,拉伸试样通过自行设计的夹头安装固定在微机控制的电子万能试验机(型号:UTM5000)上,电子万能拉伸试验机的承载能力为50 kN;使用可编程的VIS-200A型脉冲电源及VIB-10KB型变压器为拉伸过程提供所需的直流脉冲电流,通过紫铜电极对将脉冲电流引入到试样中,为保证通电拉伸过程中电流与万能试验机的绝缘,分别在上下夹头与试验机接头处添加云母纸,并对连接销表面喷涂绝缘漆进行处理.通电拉伸过程中采用K型热电偶记录试样标距中间段的温度变化,拉伸过程中万能拉伸机上横梁移动速度为3 mm/min(应变速率为10-3).
|
图 3 脉冲电流辅助拉伸实验装置示意图(a)及实验装置(b) Figure 3 The schematic(a) of an experimental set-up for EAT(b) |
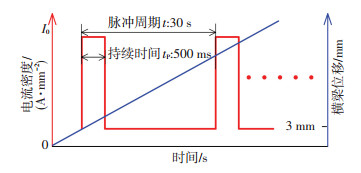
为研究脉冲峰值电流密度对6063T4力学性能的影响,对室温条件下的试样进行了拉伸测试,分别选取100,120,140 A/mm2的3种不同峰值电流密度的矩形脉冲波进行通电拉伸,脉冲电流作用时间为0.5 s,为便于分析通电拉伸中试样温升对材料性能的影响,脉冲电流作用时应排除前一脉冲电流作用时所产生的温升影响,因此,两脉冲电流作用时间间隔要足够长,通过实验探索所选用的脉冲周期为30 s(此脉冲周期能够使得下一脉冲电流作用前试样温度基本降为室温).实验过程中,当万能拉伸试验机上横梁位移达到3 mm时(材料已进入塑性变形阶段,所对应的真实应变为0.058)进行通电拉伸,其示意图如图 4所示.为保证实验的可重复性,针对每组电参数分别进行了5次实验,取有较好重复性的几组数据进行分析.
|
图 4 试样拉伸过程中所使用的周期性电脉冲示意图 Figure 4 A schematic of periodic electropulsing during the tensile displacement of a specimen of EAT |
采用K型热电偶在通电过程中对试样中段温度进行测量,由于本实验所选择的脉冲间隔时间较长,在单脉冲电流作用时温度急剧升高,在脉冲间隔内,由于热量的耗散,试样温度趋于室温,表 2呈现的是3种电流密度的脉冲电流作用时的最高温升, 可根据下式得到理论温升[15]:
| 表 2 不同电流密度下试样最高温升(室温25 ℃) Table 2 Maximum temperature rise of specimen at different electric current (room temperature 25 ℃) |
| $ \Delta {T_{\rm{c}}} = {(c\rho {s^2})^{-1}}\smallint _0^{{t_{\rm{p}}}}\gamma {I^2}{\rm{d}}t = {\left( {c\rho } \right)^{-1}}{J^2}\gamma {t_{\rm{p}}}. $ | (1) |
式(1)中各参数的物理意义列于表 3,通过理论计算得到的温升如表 2所示,3种不同电流密度条件下电能转化为温升的效率分别为66.27%,62.59%,63.1%,这与文献[16]所研究的5052铝合金的通电过程中焦耳热转化为温升的效率相似(60%左右).
| 表 3 6063T4铝合金板热电物理性能参数 Table 3 Therm-electricity parameter of the 6063T4 aluminum alloy sheet |
图 5所示是无电流条件下以及不同峰值电流密度下所获得的拉断试样,图 6为其对应的应力应变曲线.

|
图 5 不同峰值电流密度下所获得的拉断试样 Figure 5 The fracture specimens obtained at different electric current density |
|
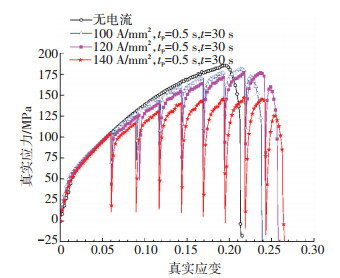
图 6 不同峰值电流密度下获得的应力应变曲线 Figure 6 Stress-strain curves obtained at different electric current density |
在无脉冲电流的拉伸过程中,流动应力随着应变的增加而不断增加,从而呈现出明显的加工硬化现象,且在发生断裂时的抗拉强度为185 MPa,而应变约为0.215 5.对于电流辅助拉伸,在脉冲电流作用板料时,试样应力出现瞬间下降,Roh等[7]称之为应力降,在脉冲间隔内应力迅速上升,加工硬化现象显现,应力应变曲线呈现独特的锯齿状,由整体应力应变曲线可以看出,与无电流条件下所获得的应力应变曲线相比,在电流辅助拉伸阶段,通电条件下试样的流动应力下降,且随着电流密度的增加,下降值更加明显.在试样发生断裂时,3种不同电流密度下试样的抗拉强度分别为172, 160,126 MPa,而应变量分别为0.240 5,0.259 5,0.266 5.综上分析可知,6063T4铝合金电流辅助能够明显降低材料流动应力,提高材料塑性.
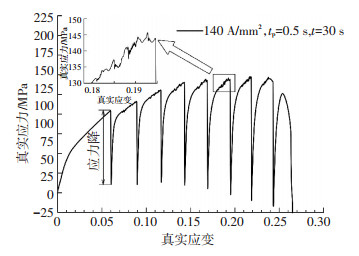
2.3 电流密度对材料动态应变时效的影响动态应变时效(Dynamic Strain Aging, DSA)是指在一定的温度和应变速率范围内,一些置换类合金以及间隙类合金在塑性变形中所发生的时效现象[18-19],具体就是材料塑性变形过程中溶质原子和移动位错相互作用的现象,反映在应力曲线中则为应力的不稳定波动,从而使得曲线呈现一定的锯齿型,即为PLC(Portevin-Le Chatelier, PLC)效应[20].图 7为峰值电流密度为140 A/mm2下获得的应力应变曲线,在电流辅助拉伸过程中呈现明显的动态应变时效现象,对于6063T4铝合金,强化相主要为金属间化合物Mg2Si,在电流辅助过程中Mg2Si相会发生溶解,从而形成游离态的Mg, Si原子,由于材料发生塑性变形时内部形成大量位错,游离态的Mg, Si原子对移动位错产生瞬时钉轧,当应力超过游离原子的阻碍时,钉轧效应解除,宏观表现为应力下降,这种钉轧及解除钉轧在材料塑性变形过程中循环往复,从而出现如图 7所得的在脉冲间隔内(应力恢复区间内)材料流动应力的不稳定波动,在材料发生不稳定变形前,随着脉冲次数的增加,DSA现象更加明显,其原因在于随着脉冲数的增加,材料内Mg2Si相更多地溶解形成游离态的Mg, Si原子,且材料内积累的位错量增加,溶质原子和位错间的相互作用更加明显.
|
图 7 峰值电流密度为140 A/mm2下获得的应力应变曲线 Figure 7 Stress-strain curves obtained at peak electric current of 140 A/mm2 |
图 8是不同峰值电流密度下第5次脉冲电流作用后获得的局部应力应变曲线,可以看到,随着峰值电流密度增加,材料DSA现象更加明显,这是因为较高密度的电流作用于材料时,在相同的应变条件下溶解出更多的游离态Mg, Si原子,其对位错的钉轧作用更加显著.

|
图 8 不同峰值电流密度下第5次脉冲电流后局部应力应变曲线 Figure 8 The local of stress-strain curve after fifth electropulsing at different electric current density |
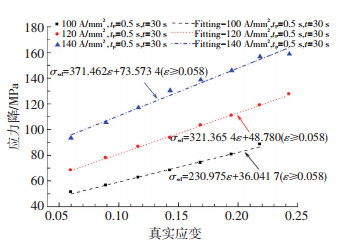
这里所指的应力降值是脉冲电流作用前后的应力差值,其示意图如图 7所示.在电流辅助拉伸过程中,单个脉冲电流作用时所产生的应力降是以下3个因素综合作用的结果[21]:1)温度诱导所产生的体积膨胀;2)焦耳热导致的材料软化;3)脉冲电流的纯电致塑性效应.图 9是本实验选用的3种电流密度下获得的应力降与真实应变之间的关系.图 9结果表明, 在脉冲电流参数不变的情况下,随着应变值的增加,应力降值基本呈线性增加,且在相同的应变条件下,脉冲电流密度越高,则应力降值越显著.通过数据点拟合所获得的应力降与应变间的线性方程的斜率可以得出随着电流密度的增大, 方程的斜率随之增大,这表明电流辅助拉伸时应力降值在较高的电流密度下表现更加显著.下面通过定性的方法来分别研究脉冲电流作用时应力降的3个诱导因素对应力降的贡献.
|
图 9 不同电流密度下应力降与真实应变间的关系 Figure 9 The relationship of stress drop and strain at different electric current |
由于本实验所选择的电参数的特点,在相同电流密度下,每个脉冲波单独作用时导致的温升基本相同(如表 2所示),且在每个脉冲波作用前试样温度接近室温,因此,引起应力降因素中的温度诱导体积膨胀所产生的热压缩应力相同,且可通过下式[22]进行计算:
| $ \sigma _{\max }^{\Delta T} = E\alpha \Delta {T_m}. $ | (2) |
式中:E为材料弹性模量; α为材料热膨胀系数; ΔTm为材料测量温升.
为定性分析焦耳热对所导致的材料软化对应力降的影响,可通过引入含有温度变量的Johnson-Cook模型[23]进行分析,其表达式为
| $ \sigma = (A + B{\varepsilon ^n})\left[{1 + C{\rm{ln}}(\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}})} \right]\left[{1-{{(\frac{{t-{t_{\rm{r}}}}}{{{t_{\rm{m}}}-{t_{\rm{r}}}}})}^m}} \right]. $ | (3) |
式中:A表示屈服强度;B和n表示应变硬化常数;C表示应变率常数;ε为等效塑性应变;
上述方程的微分形式为
| $ \begin{array}{l} {\rm{d}}\sigma = Bn{\varepsilon ^{n- 1}}(A + B{\varepsilon ^n})\left[{1 + C{\rm{ln}}(\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}})} \right]\left[{1-{{(\frac{{t-{t_{\rm{r}}}}}{{{t_{\rm{m}}}-{t_{\rm{r}}}}})}^m}} \right]{\rm{d}}\varepsilon + \\ C(A + B{\varepsilon ^n})\frac{1}{{\dot \varepsilon }}\left[{1-{{(\frac{{t-{t_{\rm{r}}}}}{{{t_{\rm{m}}}-{t_{\rm{r}}}}})}^m}} \right]{\rm{d}}\dot \varepsilon - \\ m\left( {A + B{\varepsilon ^n}} \right)\left[{1 + C{\rm{ln}}(\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}})} \right]\frac{{{{(t -{t_{\rm{r}}})}^{m -1}}}}{{{{({t_{\rm{m}}} -{t_{\rm{r}}})}^m}}}{\rm{d}}t. \end{array} $ | (4) |
若只考虑焦耳热对应力的影响,则上述微分方程则可表示为
| $ {\rm{d}}\sigma =- m(A + B{\varepsilon ^n})\left[{1 + C{\rm{ln}}(\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}})} \right]\frac{{{{(t -{t_{\rm{r}}})}^{m -1}}}}{{{{({t_{\rm{m}}} -{t_{\rm{r}}})}^m}}}{\rm{d}}t. $ | (5) |
由式(5)可知,在材料应变及应变速率一定的条件下,随着温度的升高,材料流动应力的减少值增加,因此,其对应力降值的贡献随着温度的升高而增加.
在金属纯电致塑性效应的解释中,研究最为广泛,接受程度最高的是电子风理论[24],即在拉伸过程中,随着变形量的增加试样中积累了大量位错,材料在继续发生变形的过程中需要协调位错间的流动、克服材料中溶质原子及杂质原子的钉轧,因此,需要较大的流动应力,而直流脉冲电流的通入使得定向移动的自由电子产生促进位错移动的电子风力[25-26],在诸多研究电子风力的理论中,Klimov[27]的结果被认为更接近实际情况,其理论计算公式为
| $ f/l = \frac{1}{3}n{m^*}b{v_{\rm{F}}}({v_e}-{v_{\rm{d}}}) = \frac{{{m^*}b{v_{\rm{F}}}}}{{3e}}J. $ | (6) |
式中:f/l表示施加在单位长度位错上的力;n为电子密度(单位体积的数量);m*为电子有效质量;b为柏氏矢量的数值;vF为费米速度;ve为电子漂移速度,其大小是J/en;vd为位错速度;e为电子电量,取1.602×10-19C;J为电流密度.
从上述电子风力的理论推导可以得出的结论是当电流密度较高且有较大塑性变形时,电子风力施加在单位长度位错上的力越大,自由电子对位错移动的促进作用就愈加显著,宏观表现为应力降值更加明显.
2.5 微观组织及断口形貌图 10呈现的是不同电流密度作用下试样断口附近的金相显微组织(避开拉伸试样颈缩区域).

|
图 10 不同电流密度下试样断口区域显微组织:(a)无电流;(b)100 A/mm2;(c)120 A/mm2;(d)140 A/mm2 Figure 10 Microstructure images near fracture area of fracture specimen at different electric current: (a) No electropulsing; (b) 100 A/mm2; (c) 120 A/mm2; (d) 140 A/mm2 |
在常温下,晶粒粗大且呈现等轴状态,通过截距法所得的平均晶粒尺寸为116.6 μm(图 10(a)).在电流密度为100和120 A/mm2条件下,其显微组织与原始组织相比无明显变化,但当电流密度升高到140 A/mm2时,显微组织中靠近晶界处出现细化的等轴晶粒(图 10(d)中圆圈区域所示),如前文提到的,在此电流密度的通电拉伸过程中,试样所达到的最高温度为165 ℃,其低于6系铝合金动态再结晶温度(200 ℃左右)[2],原因在于晶界处晶界能较高且变形过程中大量位错聚集在晶界处,使得晶界处畸变能升高,同时晶界处富含溶质原子,使得晶界处易于形核;而在通电拉伸过程中由于热激活效应及电激活效应,原子扩散能力增强,从而降低了试样再结晶温度;由于此脉冲时间作用较短,晶粒来不及长大,因而在显微组织中晶界交汇处表现出细化的等轴晶粒.
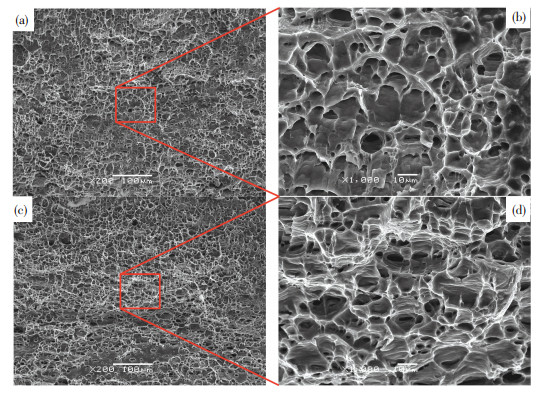
采用JSM6360LV扫描电子显微镜对拉断试样的断口形貌进行观察,图 11为不同拉伸条件下试样的断口形貌.从不同拉伸条件下的试样宏观断口(图 11(a)和(c))可以发现,断口主要为韧窝型断口且在韧窝周围及部分区域含有纤维状撕裂棱(呈亮白色),表现为韧性断裂;常规拉伸断口则表现出较少且较浅的韧窝,部分区域表现出暗灰色.随着脉冲电流的通入,试样宏观断口颈缩严重、断截面区域面积减小、纤维区明显增大且撕裂棱增多;当对比放大倍数较高的显微断口(图 11(b), (d))时可以在韧窝端部观察到较多的夹杂物、第二相粒子、硬质点,其也是韧窝形成的原因,脉冲电流辅助拉伸后得到的扫描断口处韧窝数量及深度明显增加且韧窝周围撕裂棱更加显著,断口分析表现出有较好的塑性,这与脉冲电流辅助拉伸时材料塑性增加数据相对应.
|
图 11 不同拉伸条件下试样断口形貌:(a)、(b)无电流;(c)、(d)电流辅助拉伸 Figure 11 The fracture morphology of specimen under different tensile conditions: (a)、(b) no electropulsing; (c)、(d) EAT |
1) 脉冲电流作用于单向拉伸试样时使得6063T4铝合金试样温度瞬间升高,理论计算表明,3种不同电流密度条件下电能转化为温升的效率分别为66.27%,62.59%,63.1%.
2) 周期性脉冲电流的通入使得应力应变曲线表现出独特的锯齿状,随着电流密度的增加试样抗拉强度减少,延伸性提高.
3) 电流辅助拉伸过程中出现的DSA现象归因于游离态的Mg,Si原子对位错的钉轧效应,且随着电流密度或脉冲数的增加DSA现象越发明显.
4) 脉冲电流辅助拉伸过程中应力降是温度诱导所产生的体积膨胀、焦耳热效应、纯电致塑性效应综合作用的结果,在电参数一定条件下,应力降值随着应变值的增加呈线性增加.
5) 脉冲电流作用下6063T4铝合金动态再结晶温度降低,在脉冲电流密度为140 A/mm2,温度达到165 ℃时显微组织中出现细化晶粒;断口形貌观察可以发现脉冲电流作用后试样断口的韧窝数量以及撕裂棱明显增多,且韧窝深度加深,这与应力应变曲线得到的延伸性增加相呼应.
| [1] | AGHION E, BRONFIN B, ELIEZER D. The role of the magnesium industry in protecting the environment[J]. Journal of Materials Processing Technology, 2001, 117(3): 381–385. DOI: 10.1016/S0924-0136(01)00779-8 |
| [2] | MAHABUNPHACHAI S, KOC M. Investigations on forming of aluminum 5052 and 6061 sheet alloys at warm temperatures[J]. Materials & Design, 2010, 31(5): 2422–2434. DOI: 10.1016/j.matdes.2009.11.053 |
| [3] | SO H, FASSMANN D, HOFFMANN H, et al. An investigation of the blanking process of the quenchable boron alloyed steel 22MnB5 before and after hot stamping process[J]. Journal of Materials Processing Technology, 2012, 212(2): 437–449. DOI: 10.1016/j.jmatprotec.2011.10.006 |
| [4] | CHUNG Y D, KANG H, CHO W S. The development of lightweight vehicle using aluminum space frame body[J]. Structure, 2000, 184(148.2): 109. |
| [5] | ZIQIAO Y D Z. History and current status of aluminum-lithium alloys research and development[J]. Materials Review, 2003, 2: 005. |
| [6] | KIM M J, LEE K, OH K H, et al. Electric current-induced annealing during uniaxial tension of aluminum alloy[J]. Scripta Materialia, 2014, 75: 58–61. DOI: 10.1016/j.scriptamat.2013.11.01 |
| [7] | ROH J H, SEO J J, HONG S T, et al. The mechanical behavior of 5052-H32 aluminum alloys under a pulsed electric current[J]. International Journal of Plasticity, 2014, 58: 84–99. DOI: 10.1016/j.ijplas.2014.02.002 |
| [8] | ROTH J, LOKER I, MAUCK D, et al. Enhanced formability of 5754 aluminum sheet metal using electric pulsing[J]. Trans North Am Manuf Res Inst SME, 2008, 36: 405–412. |
| [9] | XIE H, WANG J, PENG F, et al. An investigation of electroplastic effect on formability of AZ31B sheet metal[C]//[S.l.]: Numisheet American Institute of Physics, 2013:950-953. |
| [10] | GREEN C R, MCNEAL T A, ROTH J T. Springback elimination for Al-6111 alloys using electrically-assisted manufacturing (EAM)[J]. Trans North Am Manuf Res Inst SME, 2009, 37: 403–410. |
| [11] | XIE H Y, WANG Q, LIU K, et al. Investigation of influence of direct-current pulses on springback during V-bending of AZ31B magnesium alloy sheet[J]. Journal of Materials Processing Technology, 2015, 219: 321–327. DOI: 10.1016/j.jmatprotec.2014.12.011 |
| [12] | CONRAD H, KARAM N, MANNAN S. Effect of electric current pulses on the recrystallization of copper[J]. Scripta Metallurgica, 1983, 17(3): 411–416. DOI: 10.1016/0036-9748(83)90183-7 |
| [13] | MAKI S, ISHIGURO M, MORI K I, et al. Thermo-mechanical treatment using resistance heating for production of fine grained heat-treatable aluminum alloy sheets[J]. Journal of Materials Processing Technology, 2006, 177(1-3): 444–447. DOI: 10.1016/j.jmatprotec.2006.04.055 |
| [14] |
孙瑜, 黄继武, 赵毅, 等. 均匀化处理对6063铝合金微观组织结构的影响[J]. 热加工工艺, 2012, 41(2): 187–191.
SUN Yu, HUANG Jiwu, ZHAO Yi, et al. Effect of homogenization treatment of 6063 aluminum alloy[J]. Material & Heat Treatment, 2012, 41(2): 187–191. DOI: 10.14158/j.cnki.1001-3814.2012.02.058 |
| [15] | ZHANG W, ZHAO W S, LI D X, et al. Martensitic transformation from alpha-Ti to beta-Ti on rapid heating[J]. Applied Physics Letters, 2004, 84(24): 4872–4874. DOI: 10.1063/1.1762698 |
| [16] | HARIHARAN K, LEE M G, KIM M J, et al. Decoupling thermal and electrical effect in an electrically assisted uniaxial tensile test using finite element analysis[J]. Metallurgical and Materials Transactions A-Physical Metallurgy and Materials Science, 2015, 46a(7): 3043–3051. DOI: 10.1007/s11661-015-2879-3 |
| [17] |
王祝堂, 田荣璋. 铝合金及其加工手册[M]. 长沙: 中南大学出版社, 2000.
WANG Zhutang, TIAN Rongzhang. Aluminum alloy and manual processing handbook[M]. Changsha: Central South University press, 2000. |
| [18] | CHENG J, NEMAT-NASSER S, GUO W. A unified constitutive model for strain-rate and temperature dependent behavior of molybdenum[J]. Mechanics of Materials, 2001, 33(11): 603–616. DOI: 10.1016/S0167-6636(01)00076-X |
| [19] | MCCORMICK P. The Portevin-Le Chatelier effect in a pressurized low carbon steel[J]. Acta Metallurgica, 1973, 21(7): 873–878. DOI: 10.1016/0001-6160(73)90144-2 |
| [20] | FRESSENGEAS C, BEAUDOIN A J, LEBYODKIN M, et al. Dynamic strain aging: A coupled dislocation-solute dynamic model[J]. Materials Science and Engineering A-Structural Materials Properties Microstructure and Processing, 2005, 400: 226–230. DOI: 10.1016/j.msea.2005.02.073 |
| [21] | LEE J, KIM S J, LEE M G, et al. Experimental and numerical study on the deformation mechanism in AZ31B Mg alloy sheets under pulsed electric-assisted tensile and compressive tests[J]. Metallurgical and Materials Transactions A-Physical Metallurgy and Materials Science, 2016, 47a(6): 2783–2794. DOI: 10.1007/s11661-016-3492-9 |
| [22] | TANG D, ZHOU B, CAO H, et al. Thermal stress relaxation behavior in thin films under transient laser-pulse heating[J]. Journal of applied physics, 1993, 73(8): 3749–3752. DOI: 10.1063/1.352907 |
| [23] | JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics, 1983: 541-547. |
| [24] |
刘泾源. 脉冲电流在轻合金超塑变形中的宏微观作用机制[D]. 哈尔滨: 哈尔滨工业大学, 2015. LIU Jingyuan. Effect of electric current on micro-macro mechanism of light alloy superplastic deformation[D].Harbin: Harbin Institute of Technology, 2015. |
| [25] | OKAZAKI K, KAGAWA M, CONRAD H. A study of the electroplastic effect in metals[J]. Scripta Metallurgica, 1978, 12(11): 1063–1068. DOI: 10.1016/0036-9748(78)90026-1 |
| [26] | OKAZAKI K, KAGAWA M, CONRAD H. An evaluation of the contributions of skin, pinch and heating effects to the electroplastic effect in titatnium[J]. Materials Science and Engineering, 1980, 45(2): 109–116. DOI: 10.1016/0025-5416(80)90216-5 |
| [27] | KLIMOV K, SHNYREV G, NOVIKOV I, et al. Electroplastic rolling of wire into strip with sections in the micron range from tungsten and its alloys with rhenium[J]. Izv Akad Nauk SSSR Met, 1975(4): 143–145. |
 2018, Vol. 26
2018, Vol. 26


