2. 中国科学院材料力学行为和设计重点实验室(中国科学技术大学),合肥 230026
2. CAS Key Laboratory of Mechanical Behavior and Design of Materials(University of Science and Technology of China), Hefei 230026, China
胶料挤出过程是汽车轮胎行业的关键工序之一.一方面,由于螺杆几何构型复杂,使得胶料在挤出过程中处于一种非常复杂的三维流动模式;另一方面,由于橡胶材料是一种黏度很高的非牛顿流体,使得胶料在流场剪切作用下黏性生热非常严重,从而导致胶料温度上升,而温度升高又以降低胶料黏度的方式反作用于流场,使得流动特性改变.因此,胶料在挤出机中的流动是一种非常复杂的热力耦合过程,必须同时考虑胶料黏度随剪切速率变化和温度依赖以及由此产生的流场变化.对于胶料挤出这种复杂的热力耦合问题, 仅依靠实验研究费时费力,而数值模拟方法是一种较为有效的辅助研究办法.螺杆非等温挤出过程的数值模拟存在以下难点:1)如何建立包含运动螺杆和静止机筒的复杂几何模型,其中计算区域在求解过程中不断变化;2)如何准确描述胶料的非牛顿流变特性和温度依赖性;3)如何确定非等温求解中机筒壁面的温度边界条件.
Syrjälä[1]和Ghorrishy等[2]将“缠绕”在螺杆基圆柱上的螺槽“展开”成一条狭长的沟槽,沟槽的底面和2个侧面保持静止不动,而顶面(机筒壁)运动方向与实际胶料前进方向成一个螺旋角角度.在此简化模型基础上,分别研究了纯黏非牛顿流体和热塑性弹性体(TPE)在螺槽中的流动过程,但该模型显然不能准确模拟聚合物熔体在挤出机中的真实流动.此外,在温度场的计算中,Syrjälä只是通过在机筒壁施加人为设定的热学边界条件来求解温度场,并没有考虑黏性生热[1].为提高温度场计算的可靠性,Mousseau等[3]采用实测的机筒壁温度作为热学边界条件,同时考虑了黏性生热,计算了低密度聚乙烯(LDPE)挤出流道截面的温度场分布,并与实测结果进行了对比,发现两者吻合较好.但需要指出的是,上述仿真中需要实时监测机筒壁温度分布,这在挤出工艺现场是很难做到的.此外,上述仿真结果是基于简化的二维模型,无法获得胶料在螺杆中真实的三维流动.为准确模拟聚合物在挤出过程中的流动,Khalifeh等[4]采用有限体积法建立了单螺杆挤出机中的非等温三维流动模型,并考察了不同流变模型对计算结果的影响,结果表明,黏性模型与黏弹性模型温度场模拟结果基本一致.该文献数值仿真采用的螺杆是极度简化的单螺纹螺杆,但现在的挤出工艺中已经很少采用单螺纹螺杆,而是采用混合效果更好的双螺纹螺杆.此外,该研究中的流变模型参数是人为给定的,无法与真实材料的流变特性等效.国内,柳娟等[5]模拟了恒定转速和恒定进出口压力条件下螺棱旋向不同的单螺杆螺筒流道内聚氯乙烯(PVC-R)熔体的挤出过程,并用粒子示踪的方法统计表征了2种结构的混合能力,但是该研究只进行了等温流场的模拟,没有考虑黏性生热的影响.基于有限元软件Polyflow,陈晋南等[6-7]分别求解了聚氯乙烯(PVC)和聚丙烯(PP)熔体在等温和非等温条件下在注塑过程中的流场,结果发现,非等温条件下流道机筒截面的平均黏度比等温条件下的降低了24%.但需要指出的是,以上挤出过程的模拟工作基本上都是基于非橡胶类的聚合物,关于橡胶材料挤出过程的模拟工作相关文献很少.与其他高聚物相比,加入炭黑等增强相的橡胶材料的流变性质更加复杂,而且由此产生的黏性生热效应也更强,因此橡胶材料挤出过程的模拟也就更为困难.
本文建立具有复杂几何构型的主、副螺纹单螺杆螺槽内胶料的三维非等温流动有限元模型,并将采用Bird-Carreau模型(BC模型)和Arrhenius shear stress方程分别表征胶料黏度随剪切速率和温度的变化,同时通过热力学估算来确定合理的机筒壁热学边界条件.在此基础上,本文将求解不同转速下的速度场、温度场和压力场,并将数值计算结果与实测结果进行对比,以验证模型的可靠性.
1 计算模型图 1给出了数值计算所使用的螺杆和机筒的几何模型,该模型在进料口和挤出端分别加长, 使得胶料流动充分发展, 并在挤出机内完全充满.螺杆采取了主、副螺纹的形式,这种构型的螺杆提供了更强的剪切作用, 以保证橡胶产品的质量.此外,螺纹采用了等螺距不等深度的形式,与等深度螺纹相比,更大程度地保证了产品的压缩性能和致密性[8-9].本文采用六面体网格对胶料进行划分,网格数为32 760.螺杆几何构型复杂,用四面体网格对其划分,网格数为123 751.胶料和螺杆分开建模,采用网格重置技术(Mesh Superposition Technique,MST)将二者结合起来计算[10],这就很好地解决了由于计算区域持续变化而需要不断重新划分相应网格的问题.
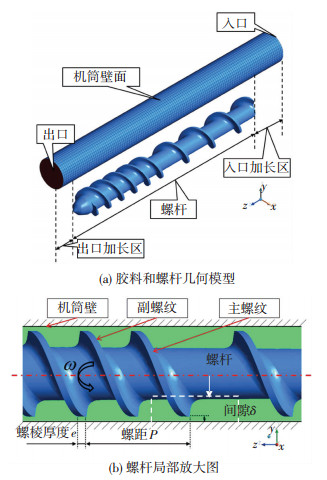
|
图 1 数值计算模型 Figure 1 The geometrical view of the simulation model: (a) schematic view of flow domain and the moving part; (b) a detailly local enlarged drawing of the screw configuration |
根据胶料的黏度以及进料量可以估算出挤出流动中的雷诺数Re < 10-1,这表明胶料在挤出过程中处于层流状态;由于胶料黏度很大,相比于黏性应力,体力和惯性项可以忽略,则修正后的控制方程如下.
动量方程:
| $ H(\boldsymbol{v}-{\boldsymbol{v}_{{\rm{moving}}}}) + \left( {1-H} \right)\left( {-\nabla p + \nabla \cdot \boldsymbol{T}} \right) = 0; $ | (1) |
应力张量:
| $ \boldsymbol{T} = 2\eta \left( {\dot \gamma, \theta } \right)\boldsymbol{D}; $ | (2) |
连续性方程:
| $ \nabla \cdot \boldsymbol{v} + \frac{\beta }{\eta }\Delta p = 0; $ | (3) |
能量方程:
| $ \begin{array}{l} \left( {1-H} \right)({\rho _{\rm{f}}}{c_{{\rm{pf}}}}\frac{{{\rm{D}}\theta }}{{{\rm{D}}t}}-\boldsymbol{T}:\nabla \boldsymbol{v}-\nabla \cdot ({k_{\rm{f}}}\nabla \theta )) + \\ H({\rho _{\rm{s}}}{c_{{\rm{ps}}}}\frac{{{\rm{D}}\theta }}{{{\rm{D}}t}} - \nabla \cdot ({k_{\rm{s}}}\nabla \theta )) = 0. \end{array} $ | (4) |
黏性生热:
| $ \psi = \eta {{\dot \gamma }^2}. $ | (5) |
式中:H为单位阶跃函数;v为速度矢量,m/s;p为压力,Pa;T为应力张量,Pa;η是黏度,Pa·s;
本文中胶料黏度随剪切速率的变化采用Bird-Carreau方程来描述,而黏度的温度依赖则采用Arrhenius shear stress方程来表述.
Bird-carreau law:
| $ \eta = {\eta _\infty } + ({\eta _0}-{\eta _\infty }){(1 + {\lambda ^2}{\dot \gamma ^2})^{\frac{{n-1}}{2}}}. $ | (6) |
Arrhenius law:
| $ A\left( \theta \right) = {\rm{exp}}\left( {\xi (\frac{1}{\theta }-\frac{1}{{{\theta _\alpha }}})} \right). $ | (7) |
黏度方程:
| $ \eta \left( {\theta, \dot \gamma } \right) = A\left( \theta \right)\eta \prime \left( {A\left( \theta \right)\dot \gamma } \right). $ | (8) |
式中:η∞为极限剪切黏度,Pa·s;η0为零剪切黏度,Pa·s;λ为松弛时间,s;n为非牛顿指数;ξ为参数;θ是温度,θα是参考温度,K;当θ=θα时,式(7)为A(θ)=1,式(8)简化为式(6).为了确定材料流变模型的各个参数,本文利用了橡胶加工分析仪RPA2000[11-13]测量了在不同温度和剪切速率下胶料的黏度值,这里列于表 1.
| 表 1 材料流变模型各个参数值 Table 1 Parameters of constitutive model in this simulation |
此外,进行热力耦合分析时还需用到胶料的热物性参数和螺杆材料(钢)的热物性参数,这些参数见表 2.
| 表 2 胶料的热物性参数和螺杆材料(钢)的热物性参数 Table 2 Parameters of thermal properties in this simulation |
需要指出的是,表 2中胶料的比热容由差式扫描量热仪[14-15]测量得到,该参数基本随温度线性上升,因此本文中表示为
| $ {c_{{\rm{pf}}}}(\theta ) = 1\;500 + \frac{{500}}{{180}}(\theta-293.15). $ | (9) |
对于本文研究的胶料流动热力耦合问题,需要同时施加运动学边界条件和热学边界条件,如表 3所示.
| 表 3 边界条件 Table 3 Boundary conditions |
表 3中,u、v、w分别为X、Y、Z方向上的速度分量;Q为入口体积流量;fz为法向应力.初始温度为胶料刚进入热喂料螺杆进料口处的实测温度.机筒壁面设置绝热边界条件的原因是机筒内壁真实的温度很难直接测量得到,且后面的热力学估算结果表明, 胶料与机筒壁之间的热传递对自身温度场的影响较小.
3 结果及讨论对于三维非等温流动过程的数值模拟,需要求解的未知量有3个速度分量(u, v, w)、压力p以及温度θ.由于控制方程中对流项的存在和材料黏度对剪切速率和温度的依赖关系,使得最终需要求解的代数方程组是非线性的,为此本文利用Picard迭代进行插值计算[16].此外,对于时间相关的数值模拟计算,需要指定计算时长,即胶料从进料口到挤出端这一过程中在挤出机中的停留时间,它的长短对挤出产品的性能至关重要[17],对于转速为20 r/min的工况,计算时长为21 s.
图 2(a)与图 2(b)分别给出了转速在20 r/min工况下的速度场和流线图.

|
图 2 速度场结果(20 r/min) Figure 2 Velocity results obtained by the simulation (20 r/min): (a) velocity contour on Y-Z plane; (b) streamlines of particles |
从图 2(a)可以看出, 速度最大值发生在螺旋棱的顶部,速度最小值则出现在螺杆的根部,在加长区域,由于没有螺杆转动的影响,速率相对较小;从图 2(b)可以看出,由于螺杆与机筒之间存在间隙,有些流线直接越过螺棱,从一个螺旋槽翻越到另外一个螺旋槽,这可以有效避免挤出过程中“死区”的出现.图 3给出了转速20 r/min工况下的剪切速率云图.从图 3可以看出,剪切速率分布的方式与速度分布相似,在入口加长段和出加长段域剪切速率较小,最大剪切速率发生在螺旋棱的顶部,这是因为此处速率会发生急剧的变化.由图 3还可以看出,副螺纹显著地增加了胶料受剪切的程度,这也解释了为什么生产中主、副螺纹形式是热喂料螺杆主要采用的几何构型.

|
图 3 Y-Z平面上的剪切速率云图(20 r/min) Figure 3 Local shear rate contour on Y-Z plane(20 r/min) |
图 4给出了转速20 r/min工况下的压力场.从图 4可以看出,从进料口到副螺纹起始处,压力逐渐增大,而从副螺纹到挤出端,压力逐渐减小.压力上升的原因是副螺纹的突然出现对胶料流动产生了阻碍作用,而随后压力减小一由于挤出端自由面边界条件的影响,另一则是由于胶料流动空间在螺杆头之后突然变大.图 5给出了转速20 r/min工况下的温度场.从图 5可以看出,剪切速率大的地方温度更高.由于受剪切的时间长,挤出段温度比进料段的温度高.图 6给出了螺杆头横截面上的温度场,可以看到,挤出端截面最高温度为396 K,而工厂生产线上此处的温度测量结果为393 K,两者基本吻合,这表明本文计算模型是有效的.

|
图 4 压力云图(20 r/min) Figure 4 Pressure contour(20 r/min) |
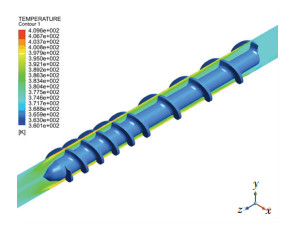
|
图 5 温度场(20 r/min) Figure 5 Temperature field on Y-Z plane(20 r/min) |
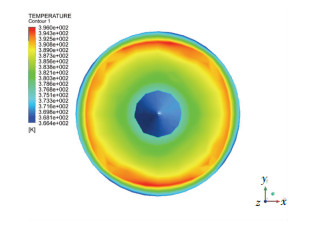
|
图 6 挤出端截面温度场 Figure 6 Temperature field on extrusion end cross-section |
此外,图 7给出了整个挤出过程的黏性生热率曲线,对其积分可以得到单次挤出过程的黏性生热量Φ1=2.1×106 J;挤出端胶料最高温度与初始温度的温差Δθ=23 K.如果假设径向温度梯度为常数,轴向温度梯度为0,则根据傅里叶定律可大致估算出21 s内通过机筒壁面散发出的热量Φ2=1.8×103 J,与生热量相比是个小量,这表明本文前面假设的机筒壁面绝热边界条件是合理的.

|
图 7 黏性生热率曲线 Figure 7 Curve of the viscous heating rate |
喂料量与转速成正比,增大转速意味着提高产量,但转速增大会使得温度和压力升高,从而影响橡胶成品的质量,为此本文计算了转速为10、15、25、30 r/min下的温度场和压力场.需要指出的是,不同转速对应的体积流量和计算时长须作出相应的调整,即体积流量与转速成正比,而计算时长与转速成反比.图 8给出了不同转速下挤出端截面的最高温度曲线.从图 8可以看出,转速升高,剪切速率增大.由黏性生热率方程
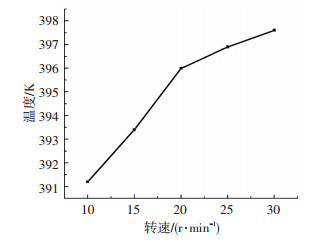
|
图 8 不同转速下的最高温度 Figure 8 Curve of the maximum temperature at different screw speed conditions |
图 9给出了不同转速下的最高压力曲线.从图 9可以看出:转速越高,进料量越大,压力上升;同时,转速上升将使得胶料的温度上升和剪切速率增大,如前所述,这将使得胶料黏度下降,从而减缓压力上升的趋势,这就解释了图中曲线的斜率下降的现象.
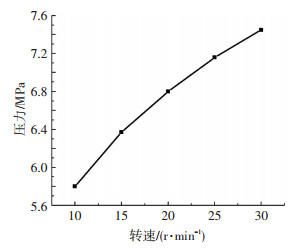
|
图 9 不同转速下的最大压力 Figure 9 Curve of the maximum pressure at different screw speed conditions |
本文建立了具有复杂几何构型的主、副螺纹单螺杆螺槽内胶料三维非等温流动的有限元模型,并采用Bird-Carreau模型和Arrhenius shear stress方程分别表征了胶料黏度随剪切速率和温度的变化,同时通过热力学估算确定了合理的机筒壁热学边界条件.在此基础上,本文得到以下结论:
1) 求解了20 r/min转速下的速度场、温度场和压力场,并将温度数值计算结果与实测结果进行了对比,两者吻合较好,这表明了模型的有效性.
2) 通过模拟发现了主、副螺纹构型的热喂料螺杆确实可以避免挤出过程中的“死区”并提供更强剪切作用;螺杆挤出段的副螺纹阻碍了胶料的流动,使得该处压力更大;由于受剪切时间更长、更强烈,胶料在挤出段温度最高.
3) 考察了不同转速下的压力和温度,结果发现挤出过程的最大压力与最高温度均随转速增大而升高,与此同时由于胶料自身的剪切变稀特性和温度依赖性,压力与温度上升的趋势会随着转速的升高而减缓.
致谢 感谢佳通轮胎(中国)研发部提供了本文研究中所使用的胶料以及测试胶料黏度的设备橡胶加工分析仪RPA2000,为本文研究提供帮助的相关人员在这里一并感谢.
| [1] | SYRJÄLÄ S. Numerical study of fully developed non-newtonian fluid flow and heat transfer in a rectangular channel with a moving wall[J]. International Communications in Heat and Mass Transfer, 1997, 24(1): 11–25. DOI: 10.1016/S0735-1933(96)00102-9 |
| [2] | GHOREISHY M H R, RAZAVI-NOURI M, NADERI G. Finite element analysis of a thermoplastic elastomer melt flow in the metering region of a single screw extruder[J]. Computational Materials Science, 2005, 34(4): 389–396. DOI: 10.1016/j.commatsci.2005.01.011 |
| [3] | WIELHORSKI Y, MOUSSEAU P, JARNY Y, et al. Thermal balance between viscous heating and inlet thermal condition in non stationary polymer flow through a cylindrical die[J]. International Journal of Thermal Sciences, 2011, 50(5): 769–778. DOI: 10.1016/j.ijthermalsci.2010.12.003 |
| [4] | KHALIFEH A, CLERMONT J R. Numerical simulations of non-isothermal three-dimensional flows in an extruder by a finite-volume method[J]. Journal of Non-Newtonian Fluid Mechanics, 2005, 126(1): 7–22. DOI: 10.1016/j.jnnfm.2004.12.002 |
| [5] |
柳娟, 王建. 左右旋螺筒结构对单螺杆挤出机性能的影响[J]. 高分子材料科学与工程, 2014, 30(3): 124–127.
LIU Juan, WANG Jian. Influence of left and right hand helically grooved barrels on the performance of single screw extruder[J]. Polymer Materials Science and Engineering, 2014, 30(3): 124–127. |
| [6] |
马德君, 陈晋南. 注射过程螺杆计量段三维流场的数值模拟[J]. 北京理工大学学报, 2006, 26(6): 478–483.
MA Dejun, CHEN Jinnan. Simulations of 3-D flow fields in the metering section of screw during injection molding[J]. Transactions of Beijing Institute of Technology, 2006, 26(6): 478–483. |
| [7] |
陈晋南, 王鸳鸯, 彭炯. 注射螺杆流道熔体非等温流场的数值研究[J]. 北京理工大学学报, 2007, 27(8): 723–727.
CHEN Jinnan, WANG Yuanyang, PENG Jiong. Simulation of non-isothermal flow field of melt in injecting screw[J]. Transactions of Beijing Institute of Technology, 2007, 27(8): 723–727. |
| [8] |
吕柏源, 郑晓斐, 闵鹏峰, 等. 橡胶挤出机螺杆构型分析及其几何参数的确定(上)[J]. 橡塑技术与装备, 2011, 37(10): 18–24.
LV Baiyuan, ZHENG Xiaofei, MIN Pengfeng, et al. Configuration analysis and geometric parameters determination of rubber extruder screw(Part one)[J]. China Rubber/Plastics Technology and Equipment, 2011, 37(10): 18–24. DOI: 10.3969/J.ISSN.1009-797X.2011.10.002 |
| [9] |
吕柏源, 郑晓斐, 闵鹏峰, 等. 橡胶挤出机螺杆构型分析及其几何参数的确定(下)[J]. 橡塑技术与装备, 2011, 37(11): 1–9.
LV Baiyuan, ZHENG Xiaofei, MIN Pengfeng, et al. Configuration analysis and geometric parameters determination of rubber extruder screw(Part two)[J]. China Rubber/Plastics Technology and Equipment, 2011, 37(11): 1–9. DOI: 10.3969/J.ISSN.1009-797X.2011.11.001 |
| [10] | ANSYS Polyflow User′s Guide, Release 14.0; ANSYS Inc.:Canonsburg, PA, USA, 2011 |
| [11] | YANG C, LI Z. A study of wall slip in the capillary flow of a filled rubber compound[J]. Polymer Testing, 2014, 37: 45–50. DOI: 10.1016/j.polymertesting.2014.04.009 |
| [12] | YANG C, LI Z. An integrated numerical study of coextrusion flow inside and outside the die[J]. Journal of Applied Polymer Science, 2016, 133(23): 43522. |
| [13] | YANG C, LI Z. Effects of wall slip on the rheological measurement and extrusion die design of a filled rubber compound[J]. Plastics, Rubber and Composites, 2016, 45(7): 326–331. DOI: 10.1080/14658011.2016.1198103 |
| [14] |
周湘文, 朱跃峰, 熊国平, 等. 机械混炼对碳纳米管/丁苯橡胶复合材料的影响[J]. 材料科学与工艺, 2010, 18(3): 307–312.
ZHOU Xiangwen, ZHU Yuefeng, XIONG Guoping, et al. Effects of mechanical mixing process on carbon nanotubes/ styrene butadiene rubber composite[J]. Materials Science and Technology, 2010, 18(3): 307–312. DOI: 10.11951/j.issn.1005-0299.20100303 |
| [15] |
张建, 唐文献, 赵希禄, 等. 基于混合动力学模型的橡胶压头硫化过程仿真[J]. 材料科学与工艺, 2012, 20(2): 16–22.
ZHANG Jian, TANG Wenxian, ZHAO Xilu, et al. Mixing of rubber piston curing process based on hybrid kinetic model[J]. Materials Science and Technology, 2012, 20(2): 16–22. DOI: 10.11951/j.issn.1005-0299.20120204 |
| [16] | GHIGLIA D C, ROMERO L A. Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods[J]. JOSA A, 1994, 11(1): 107–117. DOI: 10.1364/JOSAA.11.000107 |
| [17] |
殷小春, 曾文兵, 汤邦, 等. 叶片式正位移挤出机对PS/HDPE混合效果的影响[J]. 材料科学与工艺, 2014, 22(2): 24–29.
YIN Xiaochun, ZENG Wenbing, TANG Bang, et al. Mixing performance of PS/HDPE blends in a positive displacement flow type vane extruder[J]. Materials Science and Technology, 2014, 22(2): 24–29. DOI: 10.11951/j.issn.1005-0299.20140205 |
| [18] | 杨川. 轮胎生产中挤出工艺的实验研究和教值模拟[D]. 合肥: 中国科学技术大学, 2016. |
 2018, Vol. 26
2018, Vol. 26


