2. 山西省公安厅治安总队,太原 030001
2. Security Corps of Department of Public Security of Shanxi Province, Taiyuan 030001, China
爆炸焊接是通过炸药爆炸产生高温高压使得2种不同金属实现焊接的方法,其最大优点是可以使许多不同的金属通过该技术结合在一起作为复合材料,而且焊接界面的结合强度非常高且稳定.国内外学者对双金属复合板材的爆炸焊接[1-3]和影响爆炸焊接的参数[4-6]进行了大量研究.爆炸焊接不仅可以制造复合平板,而且还可以按需求和生产工艺特点利用内爆法和外爆法制备双金属复合管.邓伟等[7]利用AUTODYN模拟了铝/钛复合管的爆炸焊接过程.
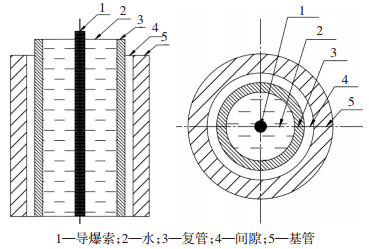
随着现代科学技术对特殊复合材料的需求,超薄材料在现代精密制造业中有广泛的应用.传统爆炸焊接炸药和材料直接接触很容易使材料产生烧伤、压痕、起皮、裂纹和撕裂等.有学者提出利用水压爆炸焊接的方法来实现薄厚度、高硬度、髙脆性复合材料的焊接,Hokamoto等[8]利用水压爆炸冲击波成功地使0.1 mm的铝箔与陶瓷ZrO2实现爆接;Manikandan等[9]利用水压爆炸爆接实现了钨箔与铜板的焊接;孙伟等[10-11]利用有限元软件ANSYS/LS-DYNA对水下爆炸冲击波驱动飞板的飞行过程进行数值模拟,验证了焊接参数合理性.对于厚度很薄、变形能力差的金属来说,传统的内爆法制备双金属复合管时炸药产生的高温可能直接烧毁金属管,但在炸药与复管之间增加水介质(如图 1所示),利用水下冲击波使得复管与基管迅速碰撞则可以避免热影响,从而实现完整匀速的焊接.
|
图 1 水压爆炸焊接法简单示意图 Figure 1 Schematic diagram of hydraulic explosion welding |
本文利用ANSYS/LS-DYNA软件建立基管、复管水压爆炸焊接的二维有限元模型,对水下爆炸冲击波驱动复管与基管碰撞过程进行了数值模拟,对复管的飞行速度和结合界面的压强进行探讨,并对不同厚度水层与基复管碰撞速度的关系进行研究,为复合管水压爆炸焊接制造提供理论支持.
1 复合管水压爆炸焊接制造数值模拟 1.1 单元类型和算法选择模型的单元类型由炸药单元、水单元、复管单元和基管单元组成,单元类型均选择2D Solid 162单元,为了提高计算精确度,选用拉格朗日算法.计算采用cm-μs-g单位制.
1.2 材料模型及状态方程炸药采用*MAT_HIGH_EXPLOSIVE_BURN材料模型,导爆索的主要成分是黑索今,用JWL状态方程;水介质采用NULL材料模型,状态方程选用Grüneisen方程;基管和复管分别采用SUS304不锈钢和Q345R碳钢材料,均选用Johnson-Cook材料模型,状态方程采用Grüneisen方程.模型的材料参数和状态方程参数,如表 1、表 2、表 3所示.
| 表 1 基管和复管的Johnson-Cook模型参数[12] Table 1 Material parameters of Johnson-Cook model |
| 表 2 炸药的JWL模型参数[13] Table 2 Material parameter s of JWL model |
| 表 3 Grüneisen状态方程参数 Table 3 Parameters of Grüneisen equation |
利用ANSYS/LS-DYNA建立复合管水压爆炸焊接过程的有限元模型,目标模型是一个垂直于轴向线的二维平面,最外层为基管,壁厚0.1 cm,复管壁厚0.05 cm,复管与基管的间隙为0.05 cm,最里层为黑索今炸药,直径0.6 cm,炸药与复管之间是水层,水层厚度设为H,H的取值分别为0.5、1.0、1.5、2.0、2.5、3.0 cm,起爆点在炸药中点处,接触类型选用关键字二维自由面面接触.图 2为水层厚度H=1.5 cm时的二维模型.

|
图 2 复合管水压爆炸焊过程的二维模型 Figure 2 2D model of composite tube manufactured by hydraulic explosion welding |
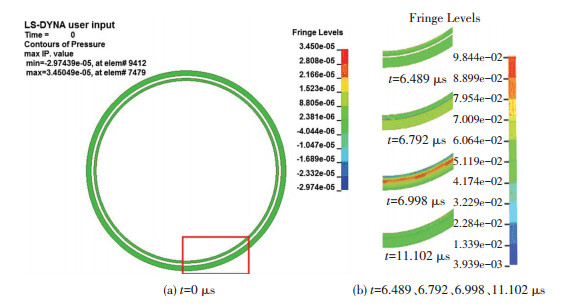
水层厚度H=1.5 cm时复合管水压爆炸焊接过程的模拟结果如图 3所示.为了方便观察,输出图片时隐藏了炸药单元和水单元的运动,初始状态如图 3(a)所示,并选取模型的一部分进行研究.图 3(b)显示的分别为起爆开始后t=6.489、6.792、6.998、11.102 μs时的水中爆炸焊接过程.炸药起爆后爆轰波形成水中冲击波,复管在冲击波瞬时高压的作用下加速向基管飞行,与基管发生迅速撞击.在碰撞点压力急剧增加,碰撞点处表现为类流体状态,并形成射流,这也是爆炸焊接的必要条件.碰撞过程中复管牢牢地结合在基管表面,没有出现烧伤、鼓包和撕裂等现象.
|
图 3 水压爆炸焊接过程 Figure 3 Process of hydraulic explosion welding: (a) t=0 μs; (b) t=6.489、6.792、6.998、11.102 μs |
只有当水下爆炸焊接的碰撞速度达到一定值时才能保证高压状态下产生射流.对于单一金属而言,可焊最小碰撞速度的经验公式[14]为
| $ {V_{{P_{\min }}}} = K\sqrt {\frac{{HV}}{\rho }} . $ | (1) |
式中:HV为管材的维氏硬度;K为0.6~1.2之间的常数,当金属材料结合表面处理很好时可取下限0.6;ρ表示管材的密度.
由于该公式中只有一种金属的性能参数,所以不适用于双金属爆炸焊接的要求.双金属焊接要求碰撞点处的高压能够使基、复管都形成射流,只要计算出它们两者中可焊压力较高的值,由此得到的可焊最小碰撞速度就是可焊接下限.可焊压力P用下式求得[14]:
| $ P = \frac{{\rho D{V_{{P \min }}}}}{2}, $ | (2) |
| $ D = C + \frac{{\lambda {V{P \min }}}}{2}. $ | (3) |
式中:VPmin, f、VPmin, b分别是基、复管2种金属能够产生射流的最小碰撞速度,可由式(1)计算;ρ为材料密度;D为冲击波在材料中的传播速度;C为材料的体积声速;λ为冲击波在材料中传播的线性系数.
利用式(2)和式(3)可以计算出复管和基管的最小可焊压力Pmin, f、Pmin, b,则双金属的最小可焊压力为
| $ {P_{{\rm{min}}}} = {\rm{max}}({P_{{\rm{min, f}}}}, {\rm{ }}{P_{{\rm{min, b}}}}). $ |
联立式(2)、(3)方程组,可以得到2种金属的碰撞速度[14-15]uf、ub:
| $ {u_{\rm{f}}} = \frac{{\sqrt {1 + 4{\lambda _{\rm{f}}}{P_{{\rm{min}}}}/({\rho _{\rm{f}}}C_{\rm{f}}^2)-1} }}{{{\lambda _{\rm{f}}}}}{C_{\rm{f}}}, $ | (4) |
| $ {u_{\rm{b}}} = \frac{{\sqrt {1 + 4{\lambda _{\rm{b}}}{P_{{\rm{min}}}}/({\rho _{\rm{b}}}C_{\rm{b}}^2)-1} }}{{{\lambda _{\rm{b}}}}}{C_{\rm{b}}}. $ | (5) |
则双金属的可焊最小碰撞速度为
| $ {V_{P{\rm{min}}}} = {\rm{max}}({u_{\rm{f}}}、{u_{\rm{b}}}). $ |
如果水中爆炸焊接的碰撞速度太大,可能会导致结合界面积累过量的能量,使得界面过度熔化,这样当从复管上表面和基管下表面反射回的稀疏波到达界面时,结合界面会分层,影响材料焊接质量.爆炸焊接上限VPmax的确定,一般采用公式[15]
| $ \begin{array}{l} {V_{P{\rm{max}}}} = 2 \times \sqrt {{\rm{ \mathit{ π} }}}\sqrt {({\rho _{\rm{f}}}{C_{P{\rm{f}}}}\sqrt {{\alpha _{\rm{f}}}} + {\rho _{\rm{b}}}{C_{P{\rm{b}}}}\sqrt {{\alpha _{\rm{b}}}} )} \times \\ \sqrt {{T_{mP{\rm{min}}}}\frac{{C_{\rm{f}}^2C_{\rm{b}}^2}}{{N(C_{\rm{f}}^2 + C_{\rm{b}}^2)}}} \frac{{4\sqrt {{t_{{\rm{min}}}}} }}{{{V_{\rm{c}}}}}\sqrt {\frac{1}{{{\rho _{\rm{f}}}{h_{\rm{f}}}}} + \frac{1}{{{\rho _{\rm{b}}}{h_{\rm{b}}}}}} . \end{array} $ | (6) |
式中:ρf、ρb分别为复管、基管的密度(kg/m3);hf、hb分别为复管、基管的厚度(m);CPf、CPb分别为复管、基管的比热(J/(kg·K));Cf、Cb分别为复管、基管的声速(m/s);αf、αb分别为复管、基管的热扩散率(m2/s);Vc为碰撞点的移动速度(m/s);Tmpmin为复管和基管熔点温度的较低值(K);tmin为反射稀疏波到达焊接界面的最短时间(s),
根据爆炸焊接窗口上限和下限,可以确定复管最佳碰撞速度VP,Stivers[16]给出的公式如下:
| $ {V_P} = {V_{P{\rm{min}}}} + 0.1({V_{P{\rm{max}}}}-{V_{P{\rm{min}}}}). $ | (7) |
把表 4中基、复管的性能参数代入上述公式中计算可得:Pmin约为5.68 GPa,VPmin=310 m/s,VPmax=1 415 m/s,VP约为420.5 m/s.
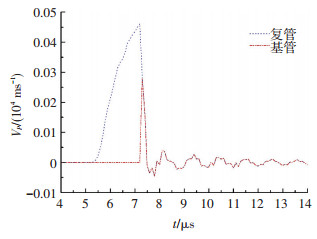
根据模拟结果绘制出水层厚度H=1.5 cm时基、复管在水压爆炸焊接过程中的碰撞结合面节点的径向速度曲线,如图 4所示:由于复管和基管有一定的间隙, 所以在炸药起爆后,复管在爆轰波形成水下冲击波的作用下加速向基管飞行,其速度将达到最大值,然后迅速下降,在该瞬间复管与基管发生碰撞.发生碰撞时,基管碰撞面开始沿与复管相同的飞行方向获得速度,两管在0.2 μs后获得相同的速度.由图 4可知, 复管的最大飞行速度约为453 m/s,满足了最小碰撞速度下限,由于模拟中复管为厚度很薄的金属,速度上限可以不用考虑.
|
图 4 基、复管碰撞结合面节点的速度曲线 Figure 4 Velocity curve of bonding interface node |
由图 4还可以看出,基、复管的运动是一个非常复杂的过程,即使是在发生碰撞后速度仍然会不停的波动,其原因是水压爆炸焊接复杂的动力学特点,由于水的惯性相对比较大,水中爆轰产物膨胀过程比较慢,会产生多次膨胀和压缩,使得复管的速度也随之产生波动大幅度的波动,所以复管与基管碰撞后,由于产生了振动源,也会形成波,造成了速度在碰撞过后仍然会出现上下波动.
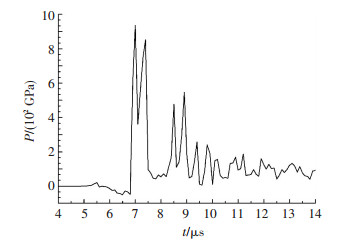
由于炸药起爆后,爆轰波以水下冲击波形式在水中传播,水下冲击波在到达复管表面时会出现马赫反射,同时复管在水下冲击波的作用下加速向基管飞行,与基管高速碰撞,在结合面处的碰撞点压力急剧升高.由图 5可知,其压力大约达到9.46 GPa,满足了双金属的最小可焊压力,保证了基、复管在碰撞点处达到类似流体的状态,产生金属射流,能够产生足够的能量驱动复管与基管发生碰撞并焊接在一起,这也是爆炸焊接的必要条件.由图 5还可以看到, 结合界面的压力存在着上下波动的情况,这是因为复管与基管碰撞后在结合界面上产生了振动源,同时碰撞点附近向水中形成反射波,这种现象一直持续到焊接结束,而压力产生负值则很大程度上是由自由界面反射回的稀疏波引起.
|
图 5 结合界面压力随时间分布曲线 Figure 5 Combined interface pressure with time distribution |
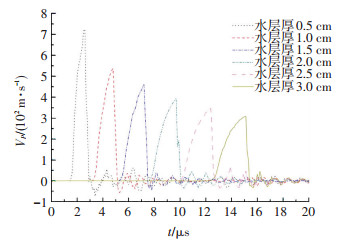
复管与基管在焊接过程中,只有当碰撞速度达到一定值时才能保证焊接的质量,速度过小则未到达焊接最小速度要求,而速度过大则会使复管撞裂或由于惯性太大出现反弹影响焊接质量.在其他条件不变的情况下,研究水层厚度对复管的最大飞行速度的影响,结果如图 6所示.由图 6可知:
|
图 6 不同厚度水层下复管飞行速度图 Figure 6 Flight velocity figure of different thickness water layers |
1) 复管的最大飞行速度随水层的厚度增加而减小,水层厚为0.5 cm速度最大,为723 m/s,1.0 cm时为546 m/s,1.5 cm时为453 m/s,2 cm时为393 m/s,2.5 cm时为338 m/s,3.0 cm时最小为296 m/s.水层厚为3 cm时复管的最大飞行速度未达到双金属的可焊最小碰撞速度,所以水层厚度应小于2.5 cm.由于炸药在水中爆炸,爆炸后产生爆轰波传入水中形成水下冲击波,冲击波会随着水层厚度的增大而逐渐减小,所以使复管的最大飞行速度变小.
2) 复管的速度从最大值降到零的时间随水层厚度的增加而增加,水层厚为0.5 cm时时间最短,为0.25 μs,1.0 cm时为0.32 μs,1.5 cm时为0.42 μs,2 cm时为0.49 μs,2.5 cm时为0.54 μs,3.0 cm时最大为0.61 μs.由于水的惯性相对比较大,水中爆轰产物膨胀过程比较慢,所以复管的速度从最大值降到最小值的时间随水层厚度的增加而增加,时间越长则有效焊接时间越长.
在本次模拟中,还设置了其他条件不变的情况下,不增加水层使炸药和复管直接接触和把1.5 cm的水层改为空气后的爆炸焊接模拟实验.在炸药和复管直接接触的模拟过程中,复管瞬间就被高能量的炸药炸毁,基管也发生严重的灼烧;而把1.5 cm的水层改为空气的模拟中,炸药产生的高温使复管出现破断、变形现象,模拟结果如图 7所示.

|
图 7 把水介质换为空气介质后的模拟结果 Figure 7 The simulation results of the water medium for air medium |
1) 通过ANSYS/LS-DYNA对不锈钢/钢复合管水压爆炸焊接制造的模型进行数值模拟研究,模拟得到的复管最大碰撞速度和压力值均满足理论计算得到的爆炸焊接速度和压力值下限要求,表明基复管可以实现焊接.对比无水层爆炸焊接,水层有效地减轻了复合管的大变形,保护了复合管的完整性.
2) 根据理论公式计算出复管的最小碰撞速度VPmin约310 m/s和最佳碰撞速度VP约420.5 m/s,可知在该尺寸下不锈钢/钢复合管水压爆炸焊接制造时水层厚度应设置在0.5~2.5 cm,而水层厚度在1.0~2.0 cm时最佳.
| [1] | ZAMANI E, LIAGHAT G H. Explosive welding of stainless steel-carbon steel coaxial pipes[J]. Journal of Materials Science, 2012, 47(2): 685–695. DOI: 10.1007/s10853-011-5841-9 |
| [2] |
李雪交, 马宏昊, 沈兆武, 等. 铝/燕尾槽钢爆炸焊接的研究[J]. 含能材料, 2016, 24(2): 188–193.
LI Xuejiao, MA Honghao, SHEN Zhaowu, et al. Explosive welding of aluminum-steel of dovetail groove[J]. Chinese Journal of Energetic Materials, 2016, 24(2): 188–193. DOI: 10.11943/j.issn.1006-9941.2016.02.014 |
| [3] |
缪广红, 马宏昊, 沈兆武, 等. 不锈钢-普碳钢的双面爆炸复合[J]. 爆炸与冲击, 2015(4): 536–540.
MIAO Guanghong, MA Honghao, SHEN Zhaowu, et al. Double sided explosive cladding of stainless steel and ordinary carbon steel[J]. Explosion and Shock Waves, 2015(4): 536–540. DOI: 10.11883/1001-1455(2015)04-0536-05 |
| [4] |
赵林升, 史长根, 葛雨珩, 等. 钛/钢双立式爆炸焊接参数优化[J]. 材料科学与工艺, 2016, 24(2): 80–84.
ZHAO Linsheng, SHI Changgeng, GE Yuheng, et al. Parameter optimization in double vertical explosive welding of Ti/steel[J]. Materials Science and Technology, 2016, 24(2): 80–84. DOI: 10.11951/j.issn.1005-0299.20160113 |
| [5] |
李继红, 蔡俊清, 刘娟娟, 等. 爆炸参数对钛/钢复合板爆炸焊接质量影响的数值模拟[J]. 兵器材料科学与工程, 2016(3): 5–8.
LI Jihong, CAI Junqing, LIU Juanjuan, et al. Numerical simulation on effect of explosi ve welding parameters on welding quality of Ti/steel composite plates[J]. Ordance Material Science and Engineering, 2016(3): 5–8. DOI: 10.14024/j.cnki.1004-244x.20160420.002 |
| [6] |
汪育, 史长根, 尤峻, 等. 双立式爆炸焊接R-δ型可焊性窗口[J]. 焊接学报, 2016(1): 59–62.
WANG Yu, SHI Changgen, YOU Jun, et al. R-δ-type weldability window of double vertical explosive welding[J]. Transactions of the China Welding Institution, 2016(1): 59–62. |
| [7] |
邓伟, 陆明, 田晓洁. 铝/钛复合管爆炸焊接三维数值模拟[J]. 焊接学报, 2014(12): 63–66.
DENG Wei, LU Ming, TIAN Xiaojie. 3D numerical simulation on explosive welding of Al/Ti composite tube[J]. Transactions of the China Welding Institution, 2014(12): 63–66. |
| [8] | HOKAMOTO K, FUJITA M, SHIMOKAWA H, et al. A new method for explosive welding of Al/ZrO2 joint using regulated underwater shock wave[J]. Journal of Materials Processing Technology, 1999, 85(98): 175–179. |
| [9] | MANIKANDAN P, LEE J O, MIZUMACHI K, et al. Underwater explosive welding of thin tungsten foils and copper[J]. Journal of Nuclear Materials, 2011, 418(1): 281–285. |
| [10] | SUN Wei, LI Xiaojie, HOKAMOTO K. Numerical simulation of underwater explosive welding process[J]. Materials Science Forum, 2014, 761: 120–125. |
| [11] |
孙伟, 李晓杰, 闫鸿浩. 合金工具钢的水下爆炸焊接[J]. 爆炸与冲击, 2016, 36(1): 107–112.
SUN Wei, LI Xiaojie, YAN Honghao, et al. Under water explosive welding of tool steel[J]. Explosion and Shock Waves, 2016, 36(1): 107–112. DOI: 10.11883/1001-1455(2016)01-0107-06 |
| [12] | 唐文龙. 不锈钢/钢复合板的爆炸焊接试验与数值模拟[D]. 南京: 南京理工大学, 2013. |
| [13] | 张宝平, 张庆明, 黄风雷. 爆轰物理学[M]. 北京: 兵器工业出版社, 2001: 160. |
| [14] |
李晓杰, 杨文彬, 奚进一, 等. 双金属爆炸焊接下限[J]. 爆破器材, 1999, 28(3): 22–26.
LI Xiaojie, YANG Wenbin, XI Jinyi, et al. The lower limit of explosive welding parameter window for bimetal[J]. Explosive Materals, 1999, 28(3): 22–26. |
| [15] |
赵铮, 王金相, 杭逸夫, 等. 双金属复合板爆炸焊接窗口研究[J]. 科学技术与工程, 2009, 9(5): 1126–1130.
ZHAO Zheng, WANG Jinxiang, HANG Yifu, et al. Research on explosive welding window of bimetal composite plate[J]. Science Technology and Engineering, 2009, 9(5): 1126–1130. |
| [16] | STIVERS S W.Computer selection of the optimum explosive loading ang welding geometry[C]//Pro 5th Int Conf on High Energy Rate Forming. Denver: Unversity of Denver, 1975, 4(2): 1-16. |
 2018, Vol. 26
2018, Vol. 26


