超声波喷丸是一种无模成形技术,可用于成形各种机械零件,并被广泛运用于汽车、航空航天等工业领域[1].相对于传统的喷丸技术,超声波喷丸成形技术可以控制喷丸区域和变形,获得更大的残余应力层.近年来,国内外对喷丸成形技术进行了大量研究.文献[2-4]中通过有限元法对喷丸过程进行数值模拟,分析其模拟结果来确定喷丸成形工艺参数. Gariepy等[5]利用试验和有限元相结合的方法研究了不同喷丸成形轨迹对板料变形的影响.Rousseau等[6]研究了超声波喷丸成形对成形后板材表面质量的影响,通过有限元模拟得出弹丸冲击速度和弹坑深度之间的关系,并利用离散元方法验证了此关系.Yin等[7]通过试验和有限元相结合的方法研究了超声波喷丸成形对AISI-1018表面形态的影响.郭超压等[8]探索了喷丸工艺参数对超声喷丸后材料表层残余应力场分布和硬化程度的影响规律,采用X射线衍射法研究了撞针式超声喷丸后7055-T7751铝合金表层残余应力和半高宽的分布情况.鲁世红等[9]利用有限元方法对2024铝合金带孔板喷丸后孔区域变形情况进行研究.
机翼带筋板能够有效提高飞机性能,减轻飞机质量.国内外对加筋板结构的弯曲成形技术已研究多年并取得一定成果.胡凯征等[10]采用了等效静态载荷温度场来模拟板加筋壁板零件的喷丸成形过程,对喷丸工艺参数进行了优化处理.刘存等[11]研究了喷丸处理对机翼加筋壁板压缩强度的影响.人工神经网络能够高度逼近非线性系统并且具有自适应和自学习能力,在工程中已经得到广泛应用.张贤杰等[12]利用BP网络,通过成形零件的曲率半径、厚度值和延伸率来预测所需的喷丸成形工艺参数.喷丸成形过程复杂,成形弧高值由多个工艺参数共同影响,现有的国内外研究无论是仿真还是实验,多为研究某一个工艺参数对成形曲率的影响规律,很少涉及多个工艺参数组合对成形曲率半径的影响.
本文利用正交试验设计并处理实验结果,研究撞针速度、撞针直径、成形轨迹间距、喷丸宽度对带筋板数控超声波成形弧高值的影响,得出最佳参数组合方案,达到最佳喷丸成形效果.以正交试验获得的数据作为样本训练BP网络,建立输入为喷丸工艺参数,输出为弧高值的神经网络模型,通过样本检验模型的准确性,从而对给定的工艺参数对弧高值进行预测.
1 正交试验设计研究正交试验法就是利用排列整齐的表(正交表)对试验方案进行统筹规划、综合比较和统计分析,利用少量的试验次数就能找到最优参数组合,得到最佳的工艺效果.超声波喷丸工艺参数多,成形过程复杂,在仿真试验之前通过设计正交表对试验参数取值进行统筹规划,采用极差分析法分析试验结果,以找到最优化的超声波喷丸工艺参数组合方案.
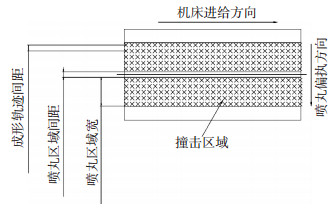
本文运用正交试验和有限元方法模拟数控超声波喷丸成形,喷丸成形轨迹如图 1所示.在数控超声波喷丸成形研究范围内选取撞针速度、撞针直径、成形轨迹间矩、喷丸区域宽度为主要的4种因素,撞针直径有3种变化即3个水平,撞针速度、成形轨迹间矩、喷丸区域宽度各有4种变化即4个水平,如表 1所示.在4种因素不同水平下根据正交理论创建L16正交试验表.利用有限元分析软件ABAQUS来模拟喷丸成形过程,进行数值模拟分析,采集数值模拟喷丸成形后的弦向弧高值作为模拟分析结果,弧高值如图 2所示.
|
图 1 喷丸成形轨迹 Figure 1 Shot peening forming trajectory |

|
图 2 弧高值 Figure 2 Arc heigh |
| 表 1 试验所选正交试验的因素及水平表 Table 1 Factors and levels of orthogonal tests selected in this experiment |
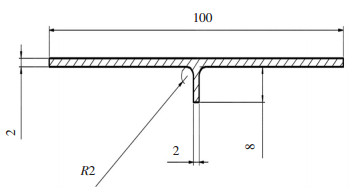
本文选用加筋板作为模拟试验件,试验件材料为2024铝合金.2024铝合金的力学性能如表 2所示.加筋板长200 mm,宽100 mm,厚2 mm.加强筋高8 mm,宽2 mm,具体截面尺寸如图 3所示.
|
图 3 加筋板横截面尺寸(单位:mm) Figure 3 Cross sectional dimension of stiffened plate |
| 表 2 2024铝合金的力学性能 Table 2 Mechanical properties of 2024 aluminum alloy |
数控超声波喷丸成形数值模拟过程可以分两步完成:第一步在Abaqus/CAE中创建仿真模型,采用Abaqus/Explicit显示分析模块,模拟数控超声波喷丸成形过程中撞针多次冲击加筋板表面的动态响应过程,得到带筋板的动态应力场分布;第二步通过加载预定义场的方式将第一步得到的带筋板动态应力场作为之后隐式分析的初始应力场,然后利用隐式分析模块,模拟夹具移除后加筋板的回弹过程,得到加筋板回弹稳定后的成形结果.数值模拟线路如图 4所示.

|
图 4 板料超声波喷丸成形有限元模拟流程图 Figure 4 Finite element simulation flow chart of sheet metal ultrasonic peen forming |
在模拟数控超声波喷丸成形过程中,确定撞针速度非常重要,撞针的初始速度由超声波变幅杆的振幅决定.Chaise等[13]研究发现,撞针的平均速度可以近似等于超声波变幅杆的最大初始速度.超声波变幅杆的最大初始速度(vinimax)计算公式为
| $ {v_{{\rm{inimax}}}} = 2{\rm{ \mathit{ π} }}Af. $ | (1) |
式中:A是变幅杆振幅,f是变幅杆振动频率.本文中,变幅杆的振幅为50 μm,振动频率为20 kHz,通过式(1)可得撞针的最大初始速度为6.3 m/s.
本文中撞针与板料之间的冲击频率远小于超声波变幅杆的振动频率.通过测量得出撞针与板料之间的冲击频率为50 Hz.因此,相邻冲击弹坑之间的距离(d)为
| $ d = {v_0}/{f_0}. $ | (2) |
式中:v0是数控机床进给速度,f0为撞针与板料之间的冲击频率.本试验中数控机床进给速度为3 000 mm/min,撞针与板料之间的冲击频率为50 Hz,因此相邻弹坑之间的间距为1 mm.
在模拟数控超声波喷丸成形过程中,撞针与板料之间的摩擦系数是一个重要的参数.本文中,设置撞针与板料之间的摩擦系数为0.25.在喷丸成形过程中,撞针几乎不变形,故假设撞针为球形刚体,带筋板可以看做是非线性动态硬化材料.由于弹塑性材料的大变形性质,因此选用Johnson-Cook (JC)模型作为材料模型.JC模型考虑到材料的加工硬化和应变率硬化,其方程式如下:
| $ \sigma = [A + B{(\varepsilon )^n}]\left[{1 + C\ln \left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]\left[{1-{{\left( {\frac{{T-{T_0}}}{{{T_{\rm{m}}}-T}}} \right)}^m}} \right]. $ | (3) |
式中:σ代表等效应力,
本文采用扫掠网格划分方式,模拟过程选用六面体减缩积分单元(C3D8R).为使模拟结果更加精确,对受冲击的局部区域进行加密处理.
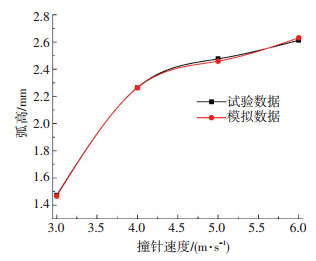
2.4 数值模拟方法验证本文通过试验进行验证了上述数值模拟方法的准确性和可靠性.试验件和模拟试验件材料相同尺寸大小一样.图 5为数控超声波喷丸前后试验件.图 6为不同撞针速度下弧高值的试验和有限元模拟对比图.由图 6可知,试验数据和模拟数据较为吻合,变化趋势一致,说明所建立的数值模拟模型准确可靠,可以使用此模型的仿真结果开展正交试验研究.

|
图 5 喷丸前后加筋板形状 Figure 5 Shape of stiffened plate before and after shot peening |
|
图 6 针速度对弧高的影响 Figure 6 Effect of the pin velocity on the arc height value |
利用极差分析法可以确定撞针速度、撞针直径、成形轨迹间距、喷丸区域宽度对成形弧高值影响的主次关系,确定每个因素的最优水平.Kjm为J列m因素水平相对的试验指标总和,
| 表 3 正交试验表及仿真结果数据 Table 3 Orthogonal test table and simulation result data |
| 表 4 正交试验分析 Table 4 Orthogonal test analysis |
| $ \overline {{K_{jm}}} = \frac{{{K_{jm}}}}{{j{\rm{列的}}m{\rm{号码水平的重复次数}}}}; $ |
j为正交试验影响因素;m为正交试验的影响因素的水平;Rj为正交试验的极差.
| $ {R_j} = {\rm{max (}}{K_{j1}}, {K_{j2}}, \cdots, {K_{jm}})-{\rm{min}}({K_{j1}}, {K_{j2}}, \cdots, {K_{jm}}). $ |
Rj指第j列因素在各个水平内试验结果的变动幅度,变动越大,说明该因素对试验结果的影响越大,反之影响越小.
根据撞针速度、撞针直径、成形轨迹间距、喷丸区域宽度各个水平所对应弧高值的平均值的大小可以确定上述4个因素取最好水平.如果要求弧高值越小,则取每个因素对应水平最小的平均值;如果要求弧高值越大,则取每个因素对应水平最大的平均值;如果要求弧高值适中,则取每个因素对应适中的平均值所对应的那个水平.但是,最优水平组合并不一定出现在正交实验设计当中.所以,根据试验要求的弧高值确定上述4种因素的较优水平组合,筛选出最佳的试验方案.
3.2 各因素正交试验结果分析计算出撞针速度、撞针直径、成形轨迹间距、喷丸区域宽度的极差并对其水平进行评估.由表 4可知,对加筋板变形弧高值影响最大的为撞针速度,其次是撞针直径,随后是喷丸区域,成形轨迹间距对变形弧高值的影响最小,A4B3C1D3为最优组合.采用该方案进行喷丸成形可以获得3.704 mm的变形弧高值.
撞针速度、撞针直径和喷丸区域的极差较大,表明撞针速度、撞针直径和喷丸区域是影响加筋板弯曲变形的重要因素.通过改变撞针速度、撞针直径和喷丸区域能够有效地对加筋板变形弧高值进行控制.
撞针直径与喷丸区域的极差相近,表明两者对加筋板弯曲变形的影响程度相近.
4 神经网络模型建立与训练BP神经网络是一种多层前反馈神经网络,该网络的主要特点是信号前向传递,误差反向传播[14].前向传递过程中,输入信号从输入层经隐含层处理传向输出层.如果输出层得到的结果和预期不同,则进入误差反向传播阶段,根据预测误差修改各层的权值,从而使预测输出逼近期望输出.现在BP神经网络已经越来越广泛地应用到解决工程中复杂的非线性系统问题.由于带筋板超声波喷丸成形的工艺参数与成形弧高值之间具有复杂的非线性关系,很难用数学方法准确建模.因此,BP神经网络以其极大的灵活性和自适应性成为解决喷丸工艺参数与弧高值之间关系的有利工具.
4.1 训练样本的选取正交试验法具有均衡分散性和综合可比性的特点,能用较少的试验反映比较全面的情况.张浩等人用正交试验的数据作为训练样本应用于人工BP神经网络,已经取得了满意的结果[15].因此,本文采用的样本为上述正交试验与数值模拟所得到的16组数据,见表 3.
4.2 BP神经网络结构的选择因为有撞针速度、撞针直径、成形轨迹间距、喷丸区域宽度4个自变量影响数控超声波喷丸弧高值,即该网络有4个输入参数,1个输出参数,可以选BP神经网络为4-10-1结构,输入层有4个节点,输出层为1个节点,隐含层有10个节点.隐含层节点转移函数选择tansig传递函数,输出层节点选择purelin函数作为转移函数.训练函数选择动态自适应学习率的梯度下降BP算法训练函数traingda,该训练函数训练速度快、精度高、效果好.训练误差控制在1%之内,满足喷丸成形后对弧高值分析的精度要求.
4.3 BP神经网络模型的检验BP神经网络训练好之后,要检测其预测弧高值的准确性.本文选用一组新的试验数据来检验预测的弧高值是否准确.即选用一组新的工艺参数用训练好的BP神经网络预测成形后的弧高值,然后通过实验验证其预测结果的准确性.实验和预测两组结果见表 5,可以看出BP神经网络预测的弧高值和实验结果相差最大,为4.69%,即该网络能很好地预测其弧高值,故可以用训练的BP神经网络来代替数值模拟.
| 表 5 BP神经网络预测结果与实验结果对比表 Table 5 Comparison of BP neural network prediction results and experimental results |
1) 对正交试验结果进行分析,对加筋板变形弧高值影响最大的为撞针速度,其次是撞针直径,随后是喷丸区域,成形轨迹间距对变形弧高值的影响最小,通过正交试验可以在给定要求的弧高值下确定上述4种因素的较优水平组合,筛选出较佳的试验方案.
2) 正交试验的数据作为样本训练BP神经网络,使用训练好的神经网络能很好的预测在给定喷丸工艺参数下的弧高值,神经网络预测值和实验结果相符较好,可以用BP神经网络预测值代替数值模拟分析值,提高工艺设计效率.
| [1] |
刘峰, 鲁世红, 张炜. 超声波喷丸技术的研究进展[J]. 航空制造技术, 2016, 509(14): 24–28.
LIU Feng, LU Shihong, ZHANG Wei. Research progress of ultrasonic shot peening technology[J]. Aeronautical Manufacturing Technology, 2016, 509(14): 24–28. DOI: 10.16080/j.issn1671-833x.2016.14.024 |
| [2] | GALLITELLI D, BOYER V, GELINEAU M, et al. Simulation of shot peening: from process parameters to residual stress fields in a structure[J]. Comptes Rendus Mécanique, 2016, 344(4/5): 355–374. |
| [3] | SEDDIK R, BAHLOUL A, ATIG A, et al. A simple methodology to optimize shot-peening process parameters using finite element simulations[J]. International Journal of Advanced Manufacturing Technology, 2017, 90(5/6/7/8): 2345–2361. |
| [4] |
康小明. 有限元法在机翼整体壁板成形中的应用[J]. 中国机械工程, 2002, 13(2): 134–136.
KANG Xiaoming. The application of finite element method in the forming of aircraft wing skin panels[J]. China Mechanical Engineering, 2002, 13(2): 134–136. |
| [5] | GARIEPY A, LAROSE S, PERRON C, et al. On the effect of the peening trajectory in shot peen forming[J]. Finite Elements in Analysis & Design, 2013, 69: 48–61. |
| [6] | ROUSSEAU T, HOC T, GILLES P, et al. Effect of bead quantity in ultrasonic shot peening: surface analysis and numerical simulations[J]. Journal of Materials Processing Technology, 2015, 225: 413–420. DOI: 10.1016/j.jmatprotec.2015.06.027 |
| [7] | YIN F, HUA L, WANG X, et al. Numerical modelling and experimental approach for surface morphology evaluation during ultrasonic shot peening[J]. Computational Materials Science, 2014, 92(5): 28–35. |
| [8] |
郭超亚, 鲁世红. 铝合金超声喷丸残余应力场[J]. 中国表面工程, 2014, 27(2): 75–80.
GUO Chaoya, LU Shihong. Residual stress of ultrasonic shot peened aluminum alloy[J]. China Surface Engineering, 2014, 27(2): 75–80. |
| [9] |
鲁世红, 成书民, 刘朝训, 等. 基于有限元仿真的带孔板超声波喷丸成形工艺[J]. 中国表面工程, 2015, 28(2): 108–113.
LU Shihong, CHENG Shumin, LIU Chaoxun, et al. Ultrasonic peening forming process in perforated plate based on finite element simulation[J]. China Surface Engineering, 2015, 28(2): 108–113. DOI: 10.11933/j.issn.1007-9289.2015.02.012 |
| [10] |
胡凯征, 吴建军, 王涛, 等. 板加筋壁板零件的喷丸成形数值模拟与工艺优化[J]. 锻压装备与制造技术, 2006, 41(3): 82–85.
HU Kaizheng, WU Jianju, WANG Tao, et al. Numerical simulation and optimization for shot peening forming process of panel with stiffeners[J]. China Metalforming Equipment & Manufacturing Technology, 2006, 41(3): 82–85. |
| [11] |
刘存, 李健, 赵谋周. 喷丸处理对机翼加筋壁板压缩强度的影响[J]. 中国表面工程, 2016, 29(1): 111–117.
LIU Cun, LI Jian, ZHAO Mouzhou. Influences of shot peening on compressive strength of wing stiffened panel[J]. China Surface Engineering, 2016, 29(1): 111–117. DOI: 10.11933/j.issn.1007-9289.2016.01.016 |
| [12] | ZHANG X J, WANG J B, WANG Y J, et al. Prediction of shot peen forming parameters of integral aircraft wing panels[J]. Materials Science Forum, 2006, 532-533: 937–940. DOI: 10.4028/www.scientific.net/MSF.532-533 |
| [13] | CHAISE T, LI J, NÉLIAS D, et al. Modelling of multiple impacts for the prediction of distortions and residual stresses induced by ultrasonic shot peening (USP)[J]. Journal of Materials Processing Technology, 2012, 212(10): 2080–2090. DOI: 10.1016/j.jmatprotec.2012.05.005 |
| [14] | 王小川. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013. |
| [15] |
张浩, 刘守城, 胡义, 等. 基于正交设计与BP神经网络优化制备Cu-Ce/TiO2的预测模型[J]. 稀土, 2015(2): 72–77.
ZHANG Hao, ZHANG Shoucheng, HU Yi, et al. Predicition model for optimizing preparation of Cu-Ce/TiO2 based on orthogonal design and back-propagation neural network[J]. Chinese Rare Earths, 2015(2): 72–77. DOI: 10.16533/j.cnki.15-1099/tf.2015.02.013 |
 2018, Vol. 26
2018, Vol. 26


