2. 辽宁科技大学 电子与信息工程学院,辽宁 鞍山 114051
2. School of Electronics and Information Engineering, Liaoning University of Science and Technology, Anshan 114051, China
现代汽车的发展趋势是环保和节能,开发集低密度与高强度于一体的钢板是实现这一目标的重要手段.Fe-Mn-Al-C钢强度和韧性高、密度低、耐冲击、抗腐蚀,被认为是第3代汽车用先进高强钢的典型钢种[1].Lee[2]发现6%含量的Mn元素可以使残留奥氏体体积分数达到30%,从而获得优异的综合性能.中锰钢(Mn含量5%~12%)可以满足汽车钢发展需求.目前,国内外关于中锰钢的研究主要集中在成分设计、性能调控等方面.Hu等研究的Fe-0.1C-5Mn钢在冷轧后的强塑积可达到31 GPa·%[3];中钢研究院开发的Fe-xC-5Mn系中锰钢形成铁素体和奥氏体双相超细晶组织,强塑积在30~48 GPa·%[4];董瑞等研发的10Mn7钢通过625 ℃保温4 h得到抗拉强度为1 177 MPa,延伸率为30.92%,强塑积为36.39 GPa·%的优良力学性能[5].但是,目前国内外关于Fe-Mn-Al-C轻质高强钢钢的热变形机制及动态再结晶尚未有系统的概念,无法为其实际生产提供理论依据[6].
本文针对一种Fe-Mn-Al-C钢模拟了单道次高温压缩变形,用Gleeble-1500热模拟机进行并记录下试样在高温变形过程中的变形温度、真应力和真应变,观察分析了组织演变规律,讨论了动态再结晶受变形温度和应变速率的影响, 并建立了反映其定量关系的本构方程,通过能量耗散绘制热加工图,得到了最佳热加工工艺参数区间.
1 实验 1.1 实验材料本文试样采用工业纯铁棒和锰、铝等合金,共20 kg在感应炉冶炼,化学成分见表 1.将铸锭锻造成尺寸为35 mm×70 mm×100 mm的板坯并淬火.机械切割取出圆柱试样,其尺寸为Φ8 mm×15 mm,并进行单道次高温压缩实验.
| 表 1 试样化学成分(质量分数/%) Table 1 Chemical compositions of the experimental steels (wt.%) |
单道次高温压缩实验的加热工艺及变形制度如下所述.实验用钢在Gleeble-1500试验机上加热到1 200 ℃(加热速度为10 ℃/s)后保温120 s均匀化处理,随后冷却到各变形温度(冷却速度为5 ℃/s),即850、900、950、1 000、1 050、1 100、1 150 ℃,保温15 s后分别以0.01、0.1、1、10 s-1变形速率压缩变形至0.6的真实应变,随后水冷,沿轴线方向将试样切开,经机械打磨抛光后用饱和苦味酸溶液及海鸥牌洗涤剂侵蚀,后期进行金相组织观察.
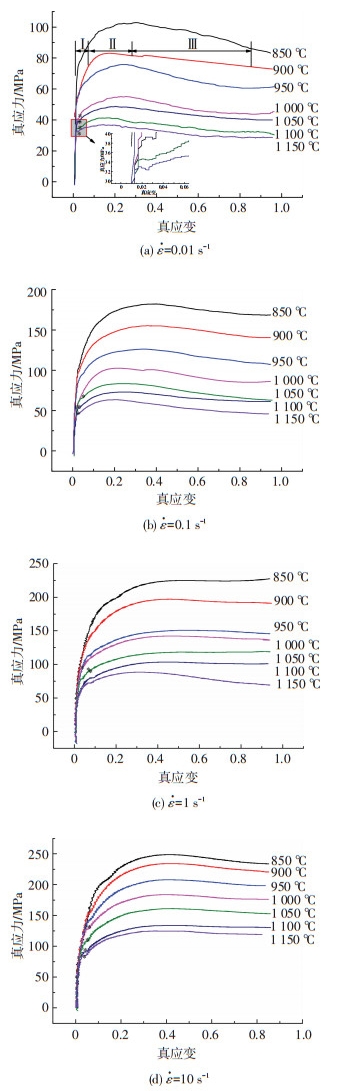
2 结果与讨论 2.1 真应力-真应变曲线用Origin软件将实验机记录的不同变形条件下的真应力与真应变关系绘制为图 1所示曲线.
|
图 1 实验用钢不同热变形条件下流变应力曲线
Figure 1 Flow stress curves of experimental steels under different thermal deformation conditions:(a) |
由图 1可以看出,在不同实验条件下,以应变速率为0.01 s-1,变形温度为900 ℃为例,实验用钢的流变应力曲线可分为3个阶段,即变形初期(ε < 0.1)由于位错增殖导致的应力随应变增加急剧上升的加工硬化阶段;到达动态再结晶临界应变(0.1≤ε < 0.3)后,流变应力达到峰值的动态软化阶段;硬化与软化相平衡(ε≥0.3),流变应力趋于稳定的稳定流变应力阶段.
用动态再结晶临界应变表征动态再结晶的发生.为了简化计算,通常利用峰值应变确定临界应变,即εc=0.6~0.8εp[7-8].对比不同变形条件下的真应力-真应变曲线可以得出,在相同的应变速率下,升高变形温度,动态再结晶更容易发生.以应变速率为0.01 s-1为例,当从850 ℃升高到1 150 ℃时,峰值应力从100 MPa减小至40 MPa,峰值应变从0.3减小至0.1;而在变形温度一定时,随着应变速率增大,动态再结晶更难发生.以850 ℃为例,当应变速率从0.01 s-1上升至10 s-1,峰值应力从100 MPa上升至250 MPa,峰值应变从0.3增大到0.5.
值得注意的是,如图 1中“*”所示,在变形初期(ε < 0.1),随着应变增加,流变应力在小范围波动,即“类屈服平台”效应[9].这是因为在变形初期,由于铁素体强度比奥氏体低而变形抗力小,根据最小阻力首先吸收应变,导致材料内部应变分布不均,铁素体动态回复发生,软化与硬化达到暂时的平衡;随着应变的进一步增大,铁素体硬化使其变形抗力大于奥氏体,导致奥氏体开始承受应变,强化发生,应力明显提高,伴随应变继续增加,奥氏体开始发生动态再结晶即软化,使得应力达到峰值后开始下降.
2.2 热变形条件对动态再结晶的影响 2.2.1 变形温度图 2(a)~(c)为实验钢应变速率为0.1 s-1不同温度下热压缩后的组织形貌,可以看出,高温变形后的组织为奥氏体和铁素体两相组织,组织为带状组织且晶粒大小分布很不均匀.变形温度为900 ℃时,奥氏体/铁素体相界及奥氏体晶粒萌生大量细小的再结晶晶粒,即开始发生再结晶,但仍有大块晶粒即再结晶进行不完全;950 ℃时,晶粒尺寸细化且分布均匀,说明奥氏体已经发生完全再结晶;1 000 ℃及以上热压缩时,奥氏体与铁素体晶粒均开始合并长大.随着变形温度的升高,晶界移动速度急剧增大,奥氏体的再结晶程度越来越大,且再结晶尺寸越来越大.而晶粒细化及组织均匀,可以提高材料的强度,这与真应力-应变曲线的结果一致.

|
图 2 不同变形条件下热压缩后的组织形貌 Figure 2 Microstructure and morphology of hot compressions under different conditions:(a) 900 ℃, 0.1 s-1 (b) 950 ℃, 0.1 s-1 (c) 1 000 ℃, 0.1 s-1 (d) 1 000 ℃, 1 s-1 |
图 2中(c)~(d)为实验钢在变形温度为1 000 ℃不同应变速率下热压缩后的组织形貌.对比可见,实验钢在变形温度为1 000 ℃应变速率为0.1 s-1条件下已完全再结晶且晶粒开始长大,而应变速率为1 s-1时有大量细小的再结晶晶粒,但再结晶进行不完全且晶粒分布不均匀.这说明低应变速率下再结晶程度更大,有利于完全再结晶的发生.
2.3 本构方程| $ \dot \varepsilon = AF(\sigma )\exp \left( {-\frac{Q}{{RT}}} \right). $ | (1) |
式中,F(σ)是应力的函数,其表达形式有以下两种情况[13]:
| $ F(\sigma ) = {\sigma ^m}, \alpha \sigma < 0.8; $ | (2) |
| $ F(\sigma ) = \exp (\beta \sigma ), \alpha \sigma > 1.2. $ | (3) |
式(2)和(3)分别适用于高温低应变速率和低温高应变速率的情况.
针对不同的变形条件,均可以经典的双曲正弦公式来描述
| $ \dot \varepsilon = A{[{\rm{sinh(}}\alpha \sigma {\rm{)}}]^n}\exp \left( { -\frac{Q}{{RT}}} \right). $ | (4) |
式中:α=β/m;
| 表 2 实验用钢峰值应力 Table 2 Peak stress of experimental steels |
将式(2)和(3)代入式(1)中,当温度T为常数时,激活能Q与T无关,等式两边取对数,并对
| $ m = \frac{{\partial \ln \dot \varepsilon }}{{\partial \ln \sigma }}, $ | (5) |
| $ \alpha = \frac{1}{m}\frac{{\partial \ln \dot \varepsilon }}{{\partial \ln \sigma }}. $ | (6) |
将式(4)等号两边取对数,并进行变形得到式(7),
| $ {\rm{ln}}\dot \varepsilon = {\rm{ln}}A + n{\rm{ln[sinh(}}\alpha \sigma )] -\frac{Q}{{RT}}. $ | (7) |
变形温度T是定值时,将上式两边对
| $ n = {\left[{\frac{{\partial \ln \dot \varepsilon }}{{\partial {\rm{ln[sinh(}}\alpha \sigma )]}}} \right]_T}. $ | (8) |
当应变速率
| $ Q = nR{\left[{\frac{{\partial \ln {\rm{[sinh(}}\alpha \sigma )}}{{\partial (1/T)}}} \right]_{\dot \varepsilon }}. $ | (9) |
分别绘制不同变形条件下的

|
图 3 |
由此,在1 123~1 423 K温度范围内,实验用钢的热变形本构方程可定量描述为
| $ \dot \varepsilon = 6.20 \times {10^9}{[{\rm{sinh}}\left( {0.009\sigma } \right)]^{4.588\;9}}{\rm{exp}}\left( { -\frac{{250\;601}}{{8.314T}}} \right). $ | (10) |
其中,热变形激活能Q为表征热变形难易程度的重要参数,受材料化学成分的影响.李德军等[14]研究了锰对Fe-Mn-Si-Al合金热变形激活能的影响,通过本构方程计算得到20Mn和25Mn的热激活能分别是361.17、411.17 kJ/mol,认为热激活能随着锰含量的增加而增加.Hamada等[15]研究了铝含量在3%~8%的Fe-25Mn钢热变形中的激活能,发现铝元素同样可以增加热变形激活能.本实验Fe-8Mn-3Al-0.2C钢变形激活能受锰、铝、碳元素综合影响,其值为250.6 kJ/mol.
2.4 热加工图变形过程中,能量一部分用于发生塑性变形,另一部分用于改变微观组织.基于动态能量耗散模型建立热加工图.其中,流变应力与应变速率之间的关系可以用下式表示[16].
| $ {\rm{log}}\sigma = a + b{\rm{log}}\dot \varepsilon + c{({\rm{log}}\dot \varepsilon )^2} + d{\rm{log}}\dot \varepsilon {)^3}. $ | (11) |
回归求得常数a、b、c、d的值,等号两边求导,整理可得应变速率敏感指数m,
| $ m = \frac{{\partial {\rm{(log}}\sigma )}}{{\partial ({\rm{log}}\dot \varepsilon )}} = b + 2c{\rm{log}}\dot \varepsilon + 3d{({\rm{log}}\dot \varepsilon )^2}. $ | (12) |
而微观组织演变能量的耗散效率η的表达式为
| $ \eta = \frac{{2m}}{{m + 1}}. $ | (13) |
在由温度和
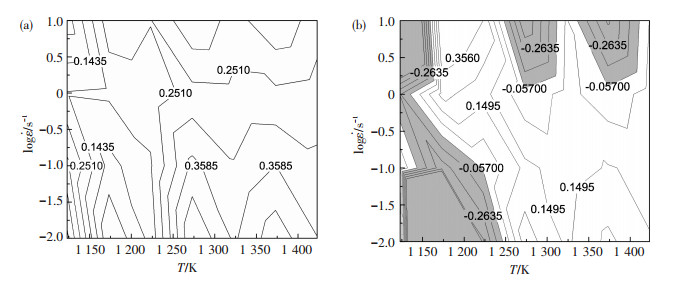
|
图 4 能量耗散图(a)及塑性失稳图(b) Figure 4 Energy dissipation chart (a) and plastic instability diagram(b) |
此外,由于在加工失稳区功率耗散效率也可能会较高,因此, 需要排除掉变形失稳区.对此,Prasad等提出了通过稳定性函数判断材料加工稳定区与失稳区[17].
| $ \varphi (\dot \varepsilon ) = \frac{{\partial {\rm{log[}}m/(m + 1)]}}{{\partial {\rm{log}}\dot \varepsilon }} + m. $ | (14) |
利用Origin软件画出稳定性函数的图像,如图 4(b)所示.当
将能量耗散图与塑性失稳图叠加,得到热加工图,如图 5所示, 可以看出,流变失稳区(即阴影部分)共有4个.第1个是在1 100~1 200 K,应变速率小于1 s-1的低温低应变速率区,由于应变速率低积累的畸变能小及晶界移动速度小,没有达到再结晶所需的驱动力;第2个失稳区是在1 100~1 150 K,应变速率大于1 s-1的低温高应变速率区,此时温度低阻碍再结晶发生且应变速率高,导致再结晶进行不均匀,产生失稳;第3和第4个失稳区主要在1 300及1 400 K的高温应变速率区,虽然此时应变速率较大畸变能累积大,但变形时间太短,来不及均匀再结晶,加工硬化大于再结晶软化,导致失稳.图 5中方框部分为最佳热加工区域.对于本实验用钢的处理工艺,发生0.6真应变的Fe-Mn-Al-C钢,变形温度为1 250~1 400 K,应变速率为0.03~0.3 s-1为其最佳热加工工艺参数区间.

|
图 5 热加工图 Figure 5 Hot processing map of experimental steels |
1) 本实验对Fe-8Mn-3Al-0.2C钢在1 123~1 423 K,0.01~10 s-1,真应变0.6条件下进行高温压缩变形,其真应力-应变曲线表现为典型的动态再结晶型曲线,即分加工硬化、动态软化及稳定流变应力3个阶段.
2) 随着变形温度的提高、应变速率的下降,峰值应力及其对应的临界应变减小,实验钢更容易发生动态再结晶.
3) 在变形初期,即ε < 0.1时,由于铁素体发生回复承受变形,流变应力曲线上会出现类似于屈服的平台.
4) 压缩后的组织为奥氏体/铁素体双相组织,动态再结晶先在铁素体内部发生,随后由奥氏体承担,随着变形温度的升高和应变速率的下降,晶粒细化组织均匀,动态再结晶完成的更充分.
5) 采用J-C模型,对给定的热变形条件下,Fe-Mn-Al-C钢的热变形数据进行拟合,得到实验用钢的热变形激活能为250.6 kJ/mol,在1 123~1 423 K温度范围内实验用钢的热变形方程可定量描述为
6) 通过绘制热加工图,得出对于本实验用钢发生0.6真应变的最佳热加工区为变形温度1 250~1 400 K,应变速率为0.03~0.3 s-1.
| [1] | CHEN S, RANA R, HALDAR A, et al. Current state of Fe-Mn-Al-C low density steels[J]. Progress in Materials Science, 2017: 2–3. DOI: 10.1016/j.pmatsci.2017.05.002 |
| [2] | LEE S, LEE S J, KUMAR S S, et al. Localized deformation in multiphase, ultra-F fine-grained 6 Pct Mn transformation-induced plasticity steel[J]. Metallurgical and Materials Transactions A, 2011, 42(12): 3638–3651. DOI: 10.1007/s11661-011-0636-9 |
| [3] |
胡俊, 刘永前, 梁文, 等. 退火温度对冷轧中锰钢力学性能的影响[J]. 钢铁研究, 2016, 44(3): 21–23.
HU Jun, LIU Yongqian, LIANG Wen, et al. Influence of annealing temperature on mechanical properties of cold-rolled medium manganese stell[J]. Research on Iron & Steel, 2016, 44(3): 21–23. |
| [4] |
王通, 徐虹, 杨广宇, 等. 中锰钢ART退火过程强塑机制的研究[J]. 热加工工艺, 2016(8): 41–45.
WANG Tong, XU Hong, YANG Guangyu, et al. Study on strong plastic mechanism of ART annealing process in manganese steel[J]. Hot Working Technology, 2016(8): 41–45. |
| [5] |
董瑞. 中锰钢组织演变规律与相变诱导塑性行为[D]. 北京: 北京科技大学, 2015. DONG Rui. Study on microstructure evolution and plasticity behavior of medium manganese steel [D]. Beijing: Beijing University of Science and Technology, 2015. http://www.cnki.com.cn/Article/CJFDTOTAL-SDYJ201503017.htm |
| [6] |
李轩, 宋仁伯, 康泰. Fe-18Mn-10Al-0.6C的热变形行为[J]. 辽宁科技大学学报, 2017(1): 48–52.
LI Xuan, SONG Rengbo, KANG Tai. The thermal deformation behavior of Fe-18Mn-10Al-0.6C[J]. Journal of Liaoning University of Science and Technology, 2017(1): 48–52. DOI: 10.11973/jxgccl201604019 |
| [7] | WEI H L, LIU G Q, XIAO X, et al. Dynamic recrystallization behavior of a medium carbon vanadium microalloyed steel[J]. Materials Science & Engineering A, 2013, 573(3): 215–221. DOI: 10.1016/j.msea.2013.03.009 |
| [8] | ABBASI S M, SHOKUHFAR A. Prediction of hot deformation behaviour of 10Cr-10Ni-5Mo-2Cu steel[J]. Materials Letters, 2007, 61(11-12): 2523–2526. DOI: 10.1016/j.matlet.2006.09.050 |
| [9] |
章小峰, 杨浩, 冷德平, 等. 铁-锰-铝-碳系低密度钢的热变形行为[J]. 机械工程材料, 2016, 40(4): 84–88.
ZHANG Xiaofeng, YANG Hao, LENG Deping, et al. Hot deformation behavior of iron manganese aluminum carbon system low density steel[J]. Mechanical Engineering Materials, 2016, 40(4): 84–88. DOI: 10.11973/jxgccl201604019 |
| [10] | MCQUEEN H J, YUE S, RYAN N D, et al. Hot working characteristics of steels in austenitic state[J]. Journal of Materials Processing Technology, 1995, 53(1-2): 293–310. DOI: 10.1016/0924-0136(95)01987-P |
| [11] | SHI H, MCLAREN A J, SELLARS C M, et al. Constitutive equations for high temperature flow stress of aluminium alloys[J]. Materials Science and Technology, 1997, 13(3): 210–216. DOI: 10.1179/026708397790302421 |
| [12] | SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136–1138. DOI: 10.1016/0001-6160(66)90207-0 |
| [13] | LI Y P, SONG R B, WEN E D, et al. Hot deformation and dynamic recrystallization behavior of austenite-based low-density Fe-Mn-Al-C steel[J]. Acta Metallurgica Sinica (English Letters), 2016, 29(5): 441–449. DOI: 10.1007/s40195-016-0406-1 |
| [14] | LI D, FENG Y, SHANGGUAN F, et al. Influences of manganese on the hot deformation of austenitic fe-mn-si-al alloys[J]. Reviews on Advanced Materialsence, 2013, 33(4): 342–347. |
| [15] | HAMADA A S, KARJALAINEN L P, SOMANI M C, et al. Deformation mechanisms in high-Al bearing high-Mn TWIP steels in hot compression and in tension at low temperatures[J]. Materials Science Forum, 2007, 550: 217–222. DOI: 10.4028/www.scientific.net/MSF.550.217 |
| [16] |
谢碧君, 郭逸丰, 徐斌, 等. GH984G18合金热加工图及再结晶图研究[J]. 材料工程, 2016, 44(9): 16–23.
XIE Bijun, GUO Yifeng, XU Bin, et al. Thermal processing and recrystallization of GH984G18 alloy[J]. Materials Engineering, 2016, 44(9): 16–23. DOI: 10.11868/j.issn.1001-4381.2016.09.003 |
| [17] | PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242[J]. Metallurgical and Materials Transactions A, 1984, 15(10): 1883–1892. DOI: 10.1007/BF02664902 |
 2018, Vol. 26
2018, Vol. 26


