WC-Co作为优异的硬质合金涂层, 具有高硬度, 高化学稳定性以及优异的耐磨损、耐腐蚀特性, 在航空、机械、汽车等行业具有普遍应用[1].由于等离子喷涂中涂层的性能受较多因素及各因素交互式影响, 难以确定出一个较为理想的工艺参数, 且工作量较大, 对制备出一种性能良好的涂层设置了障碍[2].因此, 选择一组较为理想的工艺参数至关重要.
针对热喷涂工艺的实验设计以及数据分析的研究大多采用传统的单变量实验, 而传统的单变量实验不考虑各种影响因子之间的交互作用, 只能对单个孤立的实验点进行分析[3].毛杰[4]等人以孔隙率为评价Cr2O3涂层质量的指标, 建立Box-Behnken二阶响应曲面法设计回归分析试验, 得到最优工艺参数.王东生[5]等人利用遗传神经网络对等离子喷涂进行工艺参数优化, 文献[4-5]采用了两种不同的参数优化方法.目前, 工艺参数优化的方法种类繁多, 但响应曲面法在等离子喷涂的工艺参数优化应用较少.响应曲面法是一种广泛应用于产品和工艺参数稳健性设计及工艺过程优化的统计方法[6], 主要应用于化工、制药和生物领域.通过响应曲面法可以找出影响工艺质量特征的主要因子, 优化产品或工艺质量特征, 并找出最优水平的控制范围, 以达到优化工艺参数的目的.
本文以涂层显微硬度作为响应值, 利用统计学方法重构变量与响应值之间的特征函数, 拟合出响应值的连续变量响应曲面和响应值的预测模型, 并对其模型进行方差分析和适合性检验, 对喷涂工艺参数进行优化, 同时利用BP神经网络对试验结果进行预测.
1 试验方案与设计 1.1 Box-Behnken实验设计的回归模型Box-Behnken实验设计是可以评价指标和因素间的非线性关系的一种实验设计方法[7].该实验方法没有将所有实验因素同时安排为高水平的实验组合, 对某些特殊需求的实验尤为适用.同时引进一个中心点, 并未增加轴向点, 且不存在任何极限值, 是一种简单、精确度高的设计实验方法.
在大气等离子喷涂中, 影响涂层质量的因素较多, 如:喷涂功率、喷涂距离、送粉率、主气流量等.若系统的对这些参数进行分析, 实验方案较多, 工作量繁重.本文以主气流量QAr、电流I、喷涂距离d为影响因子, 为了准确了解各加工参数对涂层显微硬度的交互式影响规律, 通常采用系统有弯曲的二次回归模型建立显微硬度与工艺参数之间的关系.
| $ \begin{array}{l} y = {\beta _0} + {\sum\nolimits_{i = 1}^k {{\beta _i}x} _i} + \sum\nolimits_{i = 1}^k {\sum\nolimits_{i = 1}^k {{\beta _{ij}}{x_i}{x_j}} } + \\ \;\;\;\;\;\sum\nolimits_{i = 1}^k {{\beta _{ii}}x_i^2 + \varepsilon .} \end{array} $ | (1) |
式中:y为显微硬度估计值; ε为实验误差; β为系数估计值; X为因素编码.
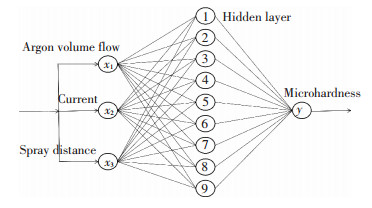
1.2 BP神经网络模型基于已有试验数据, 借助MATLAB平台, 建立WC-12Co涂层显微硬度的BP神经网络模型, 其具有自主学习及处理非线性问题的能力.BP神经网络系统由输入层、隐含层和输出层构成, 本文以喷涂距离、电流和主气流量为输入层, 以涂层显微硬度为输出层建立神经网络模型.由于隐含层的节点数量极大地影响到网络学习和计算的能力、速度和精度, 是整个BP神经网络结构是否可行的关键性因素[8], 因此, 选择合适的隐含层节点数至关重要.参照经验公式(2)[9], 在MATLAB中进行反复调试, 确定隐层单元个数q=9, BP神经网络结构如图 1所示.
| $ q = {\left( {n + m} \right)^{0.5}} + a. $ | (2) |
|
图 1 BP神经网络结构 Figure 1 Structure diagram of BP neural network |
式中:n= 3为输入层节点数; m=1为输出层节点数; a∈[1,10].
为了提高预测精度, 加快收敛速度, 对试验数据进行归一化预处理, 使其归于[0, 1]之间.数据归一化公式见式(3), 数据归一化处理后代入神经网络进行训练.
| $ {x_N} = \frac{{x-{x_{{\rm{min}}}}}}{{{x_{{\rm{max}}}}-{x_{{\rm{min}}}}}}. $ | (3) |
本试验基体材料为Q235碳素结构钢, 试样尺寸为Φ20 mm×5 mm.在喷涂前使用丙酮溶液对试样超声波清洗20 min, 然后, 采用刚玉进行喷砂粗化并用干净的空气清理试样表面, 在2 h内完成喷涂. WC-12Co涂层制备采用上海大豪喷涂公司的喷涂设备, 型号为DH-2080, 喷涂电压50 V, 氢气流量1.5 L/min, 喷枪移动速度60 mm/s, 送粉率60 g/min.WC-Co涂层采用粒径25~45 μm的WC-12Co粉末, 由北京矿冶研究总院生产.涂层截面形貌采用LED-1430VP型扫描电镜观察.涂层物相成分测定采用D&Advance型衍射仪, 采用HXD-1000TB型视频显微硬度计加载5 N载荷15 s测量涂层显微硬度, 取10个不同位置进行测量取平均值.涂层韧性的计算方法如下:
| $ {K_{{\rm{IC}}}} = \frac{{0.113H\cdot{D^{1/2}}}}{{{{(1 + {C_L}/2D)}^{3/2}}}}. $ | (4) |
式中:H为涂层维氏硬度, GPa; D为维氏压痕对角线长, μm; CL为压痕四角延伸出的裂纹长之和, μm.
假定主气流量QAr为x1, 电流I为x2, 喷涂距离d为x3.同时确定工艺参数的变化范围:QAr为2 300~2 500 L/h, I为300~400 A, d为110~130 mm.对以上3个变量进行编码, 得到水平编码表如表 1所示.
| 表 1 因素水平编码表 Table 1 Levels of independent variables |
按照Box-Behnken模型统计学实验设计要求, 等离子喷涂影响因子的编码矩阵和实测值见表 2.
| 表 2 实验结果 Table 2 The experimental results |
通过对试验参数的转换, 将试验参数经过无量纲线性编码后, 利用最小二乘法回归拟合响应值与自变量之间的多元回归模型方程.为了能够讨论影响因素之间的交互影响, 选择复相关系数R2最大的二次模型, 最终拟合二次多项式如式(5)所示.
| $ \begin{array}{l} y = 917.74-22.74{x_1}-18.33{x_2} + 114.26{x_3} + 54.44{x_1}{x_2} + \\ \;\;\;\;\;\;25.9{x_1}{x_3} + 7.45{x_2}{x_3} + 55.4x_1^2 + 10.27x_2^2 + 177.87x_3^2. \end{array} $ | (5) |
对式(5)进行方差分析及回归模型的适合性验证, 判断回归模型的显著性.通过对二次模型的方差分析(表 3)可知, P值为0.001 < 0.05;模型的失拟度的F值为3.87, P值为0.212 2>0.05.二次模型显著, 而失拟度不显著, 表明该模型能够较好地分析及预测响应值与各因素之间的关系.同时该模型的复相关系数R2为0.979 9, 信噪比精度为13.421, 更说明该模型的适合性.
| 表 3 回归模型方差分析表 Table 3 ANOVA table for the regression model |
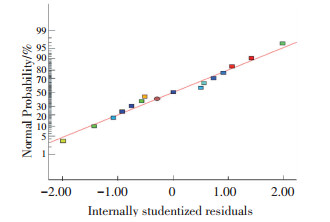
根据回归模型正态概率分布图 2的散点分布情况推断回归模型的合适性, 如果接近线性则表明模型很合适[10].由图 2可见, 回归模型的残差分析图接近线性关系, 说明回归模型比较合适, 也表明方差分析的可信度以及回归模型的有效性.
|
图 2 残差正态概率分布图 Figure 2 Normal plot of residuals |
在进行优化参数之前, 对各无量纲线性编码后因素进行效应分析.回归模型的一次项、交互项与二次项的回归系数之间线性不相关, 但二次项系数之间却线性相关[11].为了得到各单因素对回归模型的影响, 分别将模型中其他两个因素置于零水平.因此, 可以通过对3个因素的效应分析和边际效应分析来分析各因素对响应值的影响.y1、y2、y3分别为氩气流量、电流和喷涂距离的子模型.
y1=917.74-22.74x1+55.4x12;
y2=917.74-18.33x2+10.27x22;
y3=917.74+114.26x3+177.87x32.
将上述各因素子模型分别对各自因素进行求导后得到各因素在不同水平下响应值的边际方程如y′1、y′2、y′3所示.
y′1=-22.74+110.8x1;
y′2=-18.33+20.54x2;
y′3=114.26+355.74x3.
图 3为各因素子模型的回归方程曲线, 可以看到, x3对显微硬度的变异度最大, 通过方差分析, 其P为0.002 < 0.05表现显著, x3在-0.25~1, 通过改变x3的大小能使显微硬度值发生明显的正效应.x1、x2的P值分别为0.100 4、0.166 1都不显著, 曲线变异度较小且变化平缓.

|
图 3 子模型回归方程曲线 Figure 3 The regression curve of sub-model |
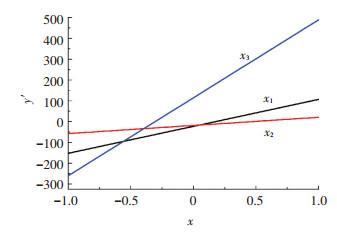
从单因素边际效应图 4中可以看出, 喷涂距离x3对涂层显微硬度影响最大, x1次之, x2最小.另外, 各因素在不同的水平时, 对显微硬度的影响程度表现的都不一样.只有通过合适的参数优化处理后才可以确定实际生产的工艺参数, 也能够准确掌握各因素对响应值的影响程度, 以确保最优工艺参数的可信度.
|
图 4 单因素边际效应图 Figure 4 The marginal effect plot of factors |
将试验数据用式(3)进行归一化处理, 得到BP神经网络训练样本矩阵, 之后进行反复训练.本文采用Bayesian Regularization函数进行训练, 训练结果如图 5所示.由于该函数训练速度较慢, 在训练到266步时达到设计要求, 此时均方误差为1.02×10-4符合设计要求.BP神经网络模型的复相关系数R2=0.999 1, 而多项式回归模型的复相关系数R2=0.979 9, 二者的复相关系数都接近1, 说明BP神经网络模型与多项式回归模型都能较好地解决非线性问题[12].图 6为涂层显微硬度的样本值与BP神经网络模型和多项式回归模型预测值的比较, 可以发现, 神经网络的平均相对误差0.46%低于多项式回归模型的平均相对误差1.56%, 多项式回归模型拟合效果略差于BP神经网络, 但二者相差不大, 说明多项式回归模型也有较好拟合的效果[13].

|
图 5 BP神经网络训练过程中均方误差变化曲线 Figure 5 Variational square error curve in BP neural network training |

|
图 6 BP神经网络和多项式预测模型与输入样本对比 Figure 6 Comparison between network and polynomial output values and sample values |
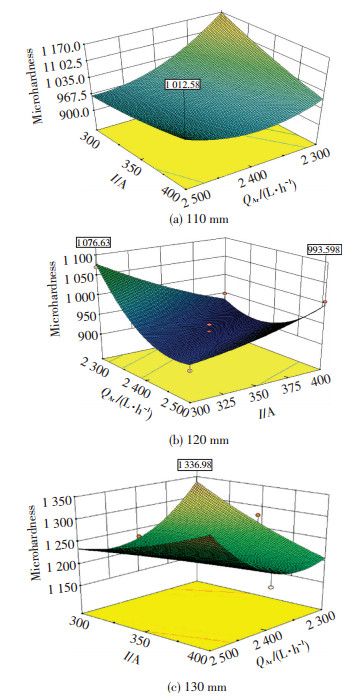
通过方差分析表 3可知, 喷涂距离d对显微硬度的影响最为显著, 与文献[5]中分析结果表现一致.氩气流量QAr与电流I的交互项对显微硬度影响显著, 其交互项P值为0.019 2 < 0.05, 表明氩气流量与电流共同作用时对显微硬度影响较大.因此, 本文建立不同喷涂距离下电流与喷涂距离的显微硬度响应曲面图来分析三因素对显微硬度的影响规律.图 7为不同喷涂距离下涂层显微硬度的响应面, 从曲面形状和变化可以直观地看出电流与氩气流量交互影响较显著且复杂.喷涂距离110 mm时, 小电流小氩气流量时获得最大硬度, 而大电流大氩气流量时对显微硬度影响不大.在中等喷距120 mm, 电流较小时, 随着氩气流量的减小涂层的显微硬度逐渐增大; 氩气流量较大时, 随着电流增大涂层的硬度显示增长的趋势.涂层的最大硬度出现在小电流小氩气流量的位置, 大电流和大氩气流量时也能够得到较大显微硬度, 但整体硬度值较大喷涂距离时的硬度有所降低.当喷距为130 mm时, 涂层的最大硬度出现在大电流大氩气流量的位置.小电流和小氩气流量时也能够得到较大显微硬度.
|
图 7 不同喷涂距离下涂层显微硬度的响应面 Figure 7 Response surface of micro-hardness under different spraying distance:(a) 110 mm; (b) 120 mm; (c) 130 mm |
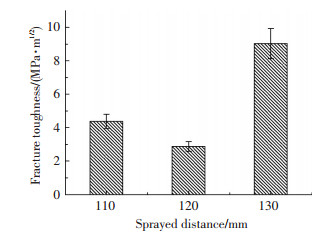
图 8为粉末与不同喷涂距离下涂层的XRD谱图, 通过对比3种不同喷涂距离的衍射结果可以看出, 不同喷涂距离下涂层中都出现了W2C相和Co6W6C相[14], 各峰的衍射强度均发生变化, 表明不同喷涂距离下的涂层出现了不同程度的脱碳.文中脱碳程度使用W2C和WC主峰的峰高比进行表示, 喷涂距离d=120 mm涂层的W2C/WC峰高比(3.4)是d=110 mm(1.3)与d=130 mm(0.9)的3倍左右, 说明其脱碳行为最为显著, 喷涂距离d=130 mm时脱碳程度最轻.图 9为不同喷涂距离的横截面形貌.喷涂距离d=120 mm时, 涂层沉积厚度(458 mm)最大, 其表面有明显的孔洞, 孔隙率最大, 致密性差.喷涂距离d=130 mm和d=110 mm时, 涂层较为致密.图 10为不同喷涂距离涂层韧性, 可见喷涂距离为130 mm时涂层具有较好的韧性, 喷涂距离为120 mm时涂层韧性差.

|
图 8 不同喷涂距离涂层XRD谱图 Figure 8 XRD diffraction patterns of coatings under different spraying distance |

|
图 9 不同喷涂距离涂层截面SEM形貌 Figure 9 SEM images of cross-section coatings under different spraying distance |
|
图 10 不同喷涂距离涂层韧性 Figure 10 Fracture toughness of coatings under different spraying distance |
在WC-Co涂层中, WC对涂层的弥散强化作用最强, WC越多, 硬质颗粒间距离越小, 颗粒间富钴粘结剂越薄, 涂层的硬度越高, 颗粒熔融充分, 颗粒之间及颗粒与基体之间碰撞叠加越致密, 涂层结合性能越好, 而Co作为粘结相进行高温烧结或复合, 使得WC-Co涂层具备高硬度和良好韧性.WC颗粒的脱碳分解程度主要取决于等离子火焰的温度及粉末颗粒在喷涂高温火焰中的停留时间[15].温度越高, 粉末高温飞行停留时间越长, 脱碳现象越严重.喷涂距离为120 mm时涂层脱碳最为严重, 也表明该喷涂距离下粒子温度相对较高, WC严重脱碳生成Co6W6C增多, 降低了涂层的硬度.Co转变为Co6W6C相, 降低了涂层的韧性, 且脱碳产生部分CO2以及氧化物夹杂, 使得涂层致密性差, 孔隙率增大.喷涂距离为130 mm时涂层氧化脱碳程度最轻, WC与Co能够很好地保留, 增加了涂层的硬度与韧性.从XRD谱图、截面形貌以及涂层韧性分析不难看出, d=130 mm时涂层各项性能均较好, 因此, 在该喷涂距离下能够得到较大显微硬度, 与响应曲面分析结果一致.
通过式(3)与喷涂距离为130 mm时响应曲面对参数进行优化.分析得到, 优先推荐能获得最大显微硬度的试验参数是电流I=390 A, 氩气流量QAr=2 500 L/h和喷距d=130 mm, 此时预测能获得的最大显微硬度为1 336.9HV0.5, 置信度为0.95.通过对该参数进行试验, 得到该参数的显微硬度为1 309.1HV0.5, 其相对误差为2.1%, 因此, 确定该参数为涂层最优参数.
4 结论1) Box-Behnken实验设计能够有效地缩短实验周期, 避免了人力财力的浪费, 在等离子喷涂工艺选择中, 可以使用该实验设计方法.同时, 基于该实验数据的多项式回归模型具有较好的拟合效果, 其复相关系数R2为0.979 9, BP神经网络的复相关系数为0.999 1, 二者拟合效果均较好.
2) 大气等离子喷涂中, 喷涂距离对涂层显微硬度的影响最为显著, 电流与氩气流量的交互作用对涂层显微硬度影响显著.响应曲面法能够清楚地展现出电流与氩气流量对显微硬度的显著性影响.
3) 涂层能够获得最大显微硬度的试验参数是电流I=390 A, 氩气流量QAr=2 500 L/h和喷距d=130 mm, 预测能获得的最大的显微硬度为1 336.9HV0.5, 实际测得该参数下的显微硬度为1 309.1HV0.5, 其相对误差为2.1%.
| [1] | VAMSI Krishna Balla, SUSMITA Bose, AMIT Bandyopadhyay. Microstructure and wear properties of laser deposited WC-12%Co composites[J]. Material Science Engineering, 2010, 527(24-25): 6677–6682. |
| [2] | ELFGHI F M. A hybrid statistical approach for modeling and optimization of RON:A comparative study and combined application of response surface methodology (RSM) and artificial neural network (ANN) based on design of experiment (DOE)[J]. Chemical Engineering Research and Design, 2016, 113: 264–272. DOI: 10.1016/j.cherd.2016.05.023 |
| [3] |
毛杰, 邓畅光, 邓春明, 等. 响应曲面法在大气等离子喷涂工艺研究中的应用[J]. 表面技术, 2013, 42(4): 65–68.
MAO Jie, DENG Changguang, DENG Chunming, et al. Application of response surface methodology to the process study of atmospheric plasma spraying[J]. Surface Technology, 2013, 42(4): 65–68. DOI: 10.16490/j.cnki.issn.1001-3660.2013.04.023 |
| [4] |
毛杰, 邓畅光, 邓春明, 等. 基于孔隙率的Cr2O3涂层工艺优化及回归分析[J]. 中国表面工程, 2013, 26(4): 38–43.
MAO Jie, DENG Changguang, DENG Chunming, et al. Process optimization and regression analysis of Cr2O3 coating based on porosity[J]. China Surface Engineering, 2013, 26(4): 38–43. |
| [5] |
王东生, 杨斌, 田宗军, 等. 基于遗传神经网络的等离子喷涂纳米ZrO2-7%Y2O3涂层工艺参数优化[J]. 焊接学报, 2013, 34(3): 10–14.
WANG Dongsheng, YANG Bing, TIAN Zongjun, et al. Process parameters optimization of nanostructured ZrO2-7%Y2O3 coating deposited by plasma spraying based on genetic algorithms and neural networks[J]. Transactions of the China Welding Institution, 2013, 34(3): 10–14. |
| [6] |
张烘州, 明伟伟, 安庆龙, 等. 响应曲面法在表面粗糙度预测模型及参数优化中的应用[J]. 上海交通大学学报, 2010, 44(4): 447–451.
ZHANG Gongzhou, MING Weiwei, AN Qinglong, et al. Application of response surface methodology in surface roughness prediction model and parameter optimization[J]. Journal of ShanghaiJiaotong University, 2010, 44(4): 447–451. |
| [7] |
张伟, 毛建国, 魏特特, 等. 基于响应曲面法的煤油发动机气门正时优化[J]. 中国机械工程, 2016(7): 933–938.
ZHANG Wei, MAO Jiangguo, WEI Tete, et al. Optimization of Valve Timing of a Kerosene Engine Based on RSM[J]. China Mechanical Engineering, 2016(7): 933–938. DOI: 10.3969/j.issn.1004-132X.2016.07.014 |
| [8] | FÁBIO Coelho Sampaio, JANAÍNA Teles de Faria, GABRIEL DUMOND de Lima Silva, et al. Comparison of response surface methodology and artificial neural network for modeling xylose-to-xylitol bioconversion[J]. Chemical Engineering Technology, 2017, 40(1): 122–129. DOI: 10.1002/ceat.v40.1 |
| [9] | SOLMAZ O, OZGOREN M. Prediction of hourly solar radiationin six provinces in turkey by artificial neural networks[J]. Journal of Energy Engineering, 2012, 138: 194–204. DOI: 10.1061/(ASCE)EY.1943-7897.0000080 |
| [10] |
杨振凯, 王海军, 刘明, 等. 基于响应曲面法的Ar-N2等离子射流特性研究[J]. 表面技术, 2016(1): 148–154.
YANG Zhenkai, WANG Haijun, LIU Ming, et al. Characteristics of the Ar-N2 plasma Jet by response surface methodology[J]. Surface Technology, 2016(1): 148–154. DOI: 10.16490/j.cnki.issn.1001-3660.2016.01.024 |
| [11] |
尹少华, 林国, 彭金辉, 等. 响应曲面法优化微波干燥碳酸稀土的实验研究[J]. 稀有金属, 2016(4): 350–355.
YIN Shaohua, LIN Guo, PENG Jinhui, et al. Optimization on experiment of microwave drying of rare earth carbonate using response surface methodology[J]. Chinese Journal of Rare Metals, 2016(4): 350–355. DOI: 10.13373/j.cnki.cjrm.2016.04.009 |
| [12] | YADAV A K, CHANDEL S. Solar radiation prediction using artificialneural network techniques:A review[J]. Renewable and Sustainable EnergyReviews, 2014, 33: 772–781. DOI: 10.1016/j.rser.2013.08.055 |
| [13] | GAO Y, XU J, LUO X, et al. Experiment research on mix design and early mechanical performance of alkali-activated slag using response surface methodology[J]. Ceramics International, 2016, 42(10): 11666–11673. DOI: 10.1016/j.ceramint.2016.04.076 |
| [14] | WOJCIECH Żórawski. The microstructure and tribological properties of liquid-fuel HVOF sprayed nanostructured WC-12Co coatings[J]. Surface Coating Technology, 2013, 220: 276–281. DOI: 10.1016/j.surfcoat.2012.11.007 |
| [15] | GENG Zhe, HOU Sihan, SHI Gaolian, et al. Tribological behaviour at various temperatures of WC-Co coatings prepared using different thermal spraying techniques[J]. Tribology International, 2016, 104: 36–44. DOI: 10.1016/j.triboint.2016.08.025 |
 2018, Vol. 26
2018, Vol. 26


