随着现代工业的发展,金属钣金成型件在日常生活中各个方面使用量逐渐增大.传统的钣金加工工艺需要先设计模具,通过模具成形出需要的零件,适合生产大批量、品种较单一的零件.金属板料渐进成形技术的优点在于不需要使用模具,可以成形比较复杂的零件,提高板料成形性能,节省制造模具的时间,节约资源,加工过程比较灵活,特别适合开发新产品和小批量生产[1-3].关于渐进成形板料壁厚分布的研究最近几年刚刚兴起,主要集中在国内几家高校,国外关于渐进成形的研究多集中在加工轨迹的优化、开发渐进成形的新材料和渐进成形的新应用等方面[4-6].
周六如[7]对板料数控渐进成形变形区厚度变化规律进行了研究,通过数控渐进成形加工了圆锥台及直壁筒形件,对成形零件变形区厚度进行测量分析,结果表明,相同厚度的板料,材料不同,成形极限厚度不同.成形极限厚度不仅与材料有关,而且与板料初始厚度有关,板料原始厚度越大,允许的变形区厚度减薄越大.Hussain等[8]采用不同铝板研究了板料减薄带的变化情况,指出板料在开始加工的弯曲部位的成形性能降低并形成减薄带.板料减薄带的范围受到板料成形性能的影响,随着板料成形性能的提高而逐渐增大,减薄带的产生是板料过度扩张的表现.Bay等[9]利用有限元模拟和拉伸试验对金字塔形件的厚度变化进行了研究,并和正弦定理的预测值进行对比,指出正弦定理仅适用于板料受纯拉伸变形的区域.Li等[10]对数控渐进成形板料的减薄带进行了有限元模拟,认为板料减薄带是阻碍渐进成形工艺大规模应用的重要缺陷,虽然通过添加多阶段成形可以在一定程度上缓解板料在减薄带部位的过度减薄,但并不能有效地解决板料的减薄带问题,而且多阶段成形的效果随着阶段数量变化也非常不稳定,没有规律可言.
综上所述,渐进成形厚度分布规律的研究尚处于初始的探索阶段,有待于进一步深入研究.板料减薄带的产生原因还不明确,哪些加工因素可以对板料厚度变化产生影响以及影响的程度和规律还不是很详细,如何避免减薄带的产生以及避免板料在减薄带破裂的措施还有待于探讨,渐进成形厚度分布规律的研究还有很大的拓展空间.就现有的研究来看,对渐进成形板料减薄带以及壁厚变化规律的研究较少,少数学者分析了渐进成形中板料减薄带和材料的关系,对板料减薄带的变化规律及其产生原因缺少本质的分析.渐进成形板料减薄带分布的研究是数控渐进成形技术中非常重要的环节,只有了解加工过程中板料减薄带的变化规律才能知道如何提供合理的加工参数和控制板料的成形过程,避免板料在“减薄带”产生裂缝,提高板料成形性能,提高板料加工利用率,减少零件破裂导致的加工失败,减少单个零件的加工时间,降低渐进成形技术的加工成本.
本文采用了理论分析和有限元模拟相结合的方法,从理论上分析了A3003铝板渐进成形过程中减薄带的产生原因,并通过有限元模拟对板料减薄带产生原因进行研究分析.
1 有限元模拟方案本文使用Dynaform软件模拟渐进成形过程,实体建模时首先通过UG建立模型,建好后保存为IGS格式文件,然后导入模拟软件Dynaform,渐进成形模型包括工具头、板料、上下压边,板料的单元类型保存为壳单元,上下夹板和工具头则保存为实体单元.网格划分时, 网格的尺寸和机床上实验板料网格保持一致,大小均为2 mm.板料采用坯料网格划分,工具头和上下夹板采用曲面网格划分,划分网格时,工具头与板料接触部位的网格紧密一些,和上下夹板接触的其他部位则可以稀疏一些.工具头曲面处的整体网格形状越圆润,生成的形状越接近半球状.接触设置根据板料表面是否涂抹润滑油,静摩擦参数分别设定为0.125和0.05,工具头和板料接触类型为点-面自动接触(Auto_One_Way_Surface_To_Surface),上下夹板与板料的接触类型为面-面自动接触(Auto_ Surface_To_Surface).定义坯料参数是模拟渐进成形过程中非常重要的一个环节.目前还没有一个统一的渐进成形板料的材料模型(包括流动准则、硬化规律、屈服准则等),软件库中的材料参数不适合应用在渐进成形的模拟中,材料参数不准确会导致渐进成形的模拟结果与实际差别较大,模拟结果不具有参考价值.经过多次尝试和查阅资料[11],本实验材料模型的FLD曲线增大了5倍,R值(R0、R45、R90)增大4倍,应力应变曲线增大1.5倍.板料的属性定义中翘曲刚度计算方法选择Belyts-Wong-Chiang,对模拟的各个零件层进行自动定位,板料不动为主工具,上下压边和工具头移动为从工具,间隙0.735 mm,等于板料的厚度,防止模拟时工具头和板料发生初始渗透.为提高模拟计算速度,增加工具头的运动速度,对于模拟结果可靠性影响可以忽略,工具头的虚拟模速度由后面对工具头施加时间-位移控制的时间决定.这里定义的工具头的速度曲线在后续的Dyn文件中需要修改.压边圈要求压紧板料,压边力为200 kN.因为Dynaform中原本只能定义一维方向的运动,为实现工具头三维方向的运动,需要对渐进成形的工具头轨迹进行定义.首先, 需要通过Dyn文件对其自由度的限制进行修改,将工具头X、Y、Z方向上的平动约束全部去掉,只约束3个方向上的转动.修改的代码不能通过软件直接模拟,通过软件模拟,则修改的代码会恢复成未修改前的初始状态,需把求解器独立出来,单独运行求解器才能进行渐进成形的模拟.
由于锥形件比较简单,加工过程中板料的变形相对比较均匀,板料不易破裂,具有较高的成形极限,能够更好适用于渐进成形板料壁厚变化的研究,本文通过有限元模拟不同加工参数渐进成形圆锥形件来研究板料减薄带的变化及其产生原因.圆锥形件开口直径为100 mm,加工参数分别为成形工具头直径、垂直进给量和成形角,具体加工参数设置如表 1所示.
| 表 1 锥形件加工参数 Table 1 Processing parameters of conical parts |
有限元模拟中采用的A3003铝板的板料初始厚度为0.735 mm,杨氏模量E=69 GPa,泊松比ν=0.33,强度系数K=191.4 MPa,抗拉强度σb=120~160 MPa,屈服强度σ0.2≥85 MPa,R0=2.37,R45=1.95,R90=2.13.
2 减薄带产生原因及有限元模拟研究至今没有任何学者提出渐进成形板料减薄带的产生原因,关于渐进成形板料减薄带的研究不多,基本都集中在加工参数对减薄带的影响以及对正弦定理预测壁厚正确性的验证.渐进成形时板料既发生弹性变形,也发生塑性变形,同时还得考虑板料初始加工区域弯曲部位的影响,板料减薄带的产生受很多因素影响,本文对渐进成形中板料的变形过程进行研究分析,对减薄带产生的原因进行了推断,并通过有限元模拟对此观点进行验证.
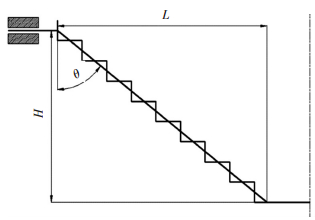
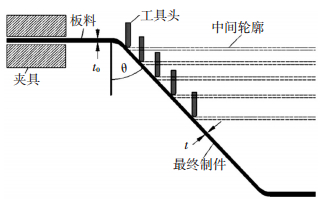
2.1 水平偏移量与垂直进给量分析渐进成形板料减薄带产生原因之前,需先了解成形工具头的进给方式,渐进成形工具头轨迹如图 1所示,工具头轨迹的位移可分为2个方向,水平方向由四周向板料中心水平偏移量,垂直方向由原始板料向下的一个垂直进给量.从板料厚度方向看,成形典型制件轨迹是一条呈台阶状轨迹,通过逐层累积成形出目标制件,水平偏移量(L)与垂直进给量(H)的关系与成形角度(θ)有关,tan θ=L/H.通过渐进成形板料厚度方向的工具头轨迹可以看出,板料斜壁是由一层层台阶状轨迹累积而成,垂直进给量越小则水平进给量也越小,台阶越多,轨迹越接近直线.理论上讲,渐进成形的板料壁厚分布是均匀的,不应该在锥口位置产生减薄带,可通过正弦定理计算成形后的板料壁厚,渐进成形过程中板料的理想变形如图 2所示.可以把板料从开始到结束的中间轮廓看成一系列同心圆,工具头按成形角度在进给方向上把同心圆直径逐渐变小,最终形成锥形件.同一层上板料周向不发生变形,变形前后尺寸不变.
|
图 1 板料横截面的工具头轨迹 Figure 1 Tool path of sheet metal cross section |
|
图 2 渐进成形板料的理想变形图 Figure 2 Ideal deformation of sheet metal incremental forming |
根据塑性变形体积不变定律,板料变形区的体积不变化[12]:
| $ {{t}_{0}}\times {{S}_{0}}=t\times S. $ | (1) |
| $ \text{因为}\ \ \ \ \ \ \ {{\mathit{S}}_{\text{0}}}=S\times \text{sin}\ \theta \text{, } $ | (2) |
| $ \text{所以}\ \ \ \ \ \ \ {{t}_{0}}\times \mathit{S}\times \text{sin}\ \theta =t\times \mathit{S}\text{, } $ | (3) |
| $ \text{即}\ \ \ \ \ \ \ t={{t}_{0}}\times \text{sin}\ \theta . $ | (4) |
式中:t0为板料初始厚度; t为目标制件厚度; S0为板料变形区初始面积; S为板料变形区成形后的面积; θ为成形角度,也称半锥角.
从式(4)可以看出,理想情况下,渐进成形板料厚度变化符合正弦定理,成形角越大,成形后板料厚度越大.当成形角过小时,板料减薄速率太大,引起板料发生破裂.
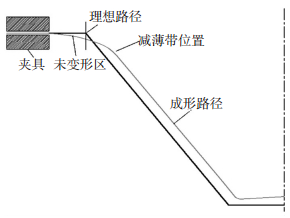
实际渐进成形时,板料壁厚的变化并不在理想情况下,板料壁厚变化也并不完全符合正弦定理的变化规律.如图 3所示,未变形区板料存在一定高度的下沉,板料在初始加工阶段并没有立即达到设计成形角度,再加上板料斜壁存在一定回弹,斜壁轮廓会比设计偏高,造成了板料在初始加工阶段存在一段角度较为平缓区域,在这段比较平缓区域,与理想路径相比,板料的变形性质发生了改变.
|
图 3 板料侧壁的实际变形与理想变形 Figure 3 Practical and ideal deformation of sheet metal wall |
当工具头进行第一层等高线的加工时,工具头与夹具之间的未变形区板料会整体产生轻微下沉,由图 1可知,垂直方向上工具头进给时,工具头是垂直向下进给的,板料与工具头之间相互垂直,没有形成板料的成形角,发生纯剪切变形.当加工第二层等高线时,未变形区板料再一次下沉,这时板料依然发生剪切变形,直至加工到n层时,垂直进给量为nΔH,工具头在水平方向上往板料中心移动了nΔL距离,这时随着工具头离未变形区的板料越来越远,板料因为发生剪切变形,厚度过度减薄,刚度降低,板料发生弯曲变形,弯曲角度逐渐达到成形角.平缓区域板料的下沉对板料成形的影响结束,板料壁厚回升,进入壁厚稳定的剪切和拉伸混合作用变形阶段.所以,渐进成形板料产生“减薄带”是由于平缓区域板料的下沉引起板料在初始加工阶段发生了剪切变形.
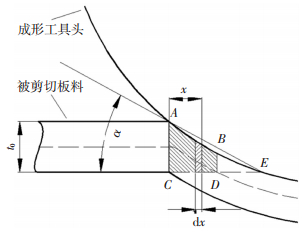
2.2 成形力分析由减薄带产生原因可知,渐进成形板料由于锥口平缓区域板料下沉的影响,在锥口边缘发生剪切变形,板料受到垂直向下的剪切力作用,那么剪切力是如何产生的呢?作者认为,随着工具头在板料表面不停地运行,在平缓区域阶段点A处会产生剪切力,板料应变主要集中在A点,且大小随着板料与水平方向的夹角α增大而减小,如图 4所示.
|
图 4 渐进成形板料的剪切受力图 Figure 4 Shear force of sheet metal incremental forming |
把弧线AB看作弦,在梯形ABCD内作用于宽度为dx微小面积上的剪切力为[7]
| $ {\rm{d}}{{p}_x}{\rm{ = }}{{q}_x}{{\rm{d}}_{x}}{ = }\tau {{t}_0}{\rm{d}}{x}{.} $ | (5) |
式中:qx为作用在接触弧AB的水平投影中单位长度上的剪切力,可以推出相对切入深度为
| $ \varepsilon \mathit{=}\frac{Z}{{{t}_{0}}}=\frac{x\text{tan}\ \alpha }{{{t}_{0}}}, $ | (6) |
微分以后得
| $ \text{d}\mathit{x=}\frac{{{t}_{0}}}{\text{tan}\ \alpha }\text{d}\varepsilon \text{.} $ | (7) |
式中,α为AB和CD间的夹角,如图 4所示.所以纯剪切力为
| $ \mathit{P}{\rm{ = }}\int {\tau {t_0}{\rm{d}}\mathit{x = }\frac{{t_0^2}}{{{\rm{tan}}\;\alpha }}} \int {\tau {\rm{d}}\varepsilon {\rm{ = }}\frac{{t_0^2}}{{{\rm{tan}}\;\alpha }}} a. $ | (8) |
式中,a为单位剪切功.
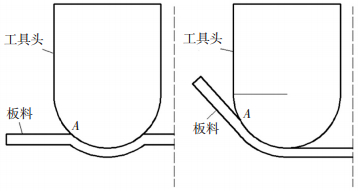
由式(7)可以看出,A点剪切力的大小和夹角α有关,随着板料持续加工变形,平缓区域不断下沉,α不断增大,剪切力随着板料成形不断减小.从板料减薄速率也可以看出,板料壁厚减薄速率从开始是逐渐减小的,此时切向的水平拉伸力正在不断增大,B点和E点受到垂直于工具头方向的挤压力作用.随着板料在平缓区域的阶段结束,板料与工具头的接触角度发生变化如图 5所示.此时板料A点剪切力减小到很小,板料减薄至厚度最小点处,由于板料边缘指向圆心的拉伸力自初始加工一直从零不断增大,板料A点受到垂直方向拉伸力和水平方向拉伸力的合力作用进入纯拉伸变形阶段,板料壁厚逐渐恢复到理论计算值左右.
|
图 5 板料与工具头接触角度的变化过程 Figure 5 Contact angle variation of sheet metal and tool |
由图 3可知,渐进成形板料的平缓区域是由未变形区域板料下沉和变形区板料的回弹造成的,所以要想对结论进行验证,只需从板料未变形区的下沉和变形区的回弹这两个方面分析,如果有限元模拟结果和结论预测一致,说明上述对板料减薄带产生原因的推测是正确的.
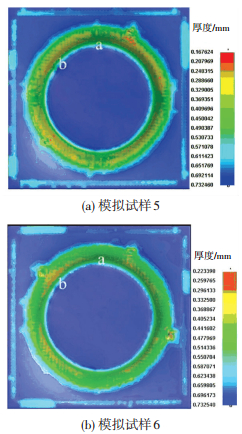
2.3.1 未变形区板料长度的影响如果减小未变形区板料长度,由图 3可知,虽然板料未变形区依然会下沉,但锥口下沉的高度会降低,板料平缓区域长度也会减小, 导致平缓区域板料长度减小,板料减薄速率不发生变化,板料减薄率和减薄范围相应都会减小,如图 6所示.
|
图 6 不同未变形区板料长度下的模拟壁厚分布 Figure 6 Simulated wall thickness distribution with different sheet metal length of no deformation zone: (a)simulation sample 5;(b)simulation sample 6 |
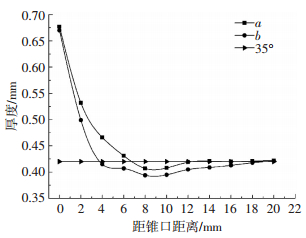
从图 7可以看到,试样5和试样6的应变分布都有一个明显特点,沿着正方形对角线处的板料变形区的应变即b点应变都比较大,在正方形四边中心部位的板料变形区的应变即a点应变都比较小,符合理论推测结果.
|
图 7 试样5的a点和b点的厚度变化曲线 Figure 7 Thickness curves of point a and b of sample 5 |
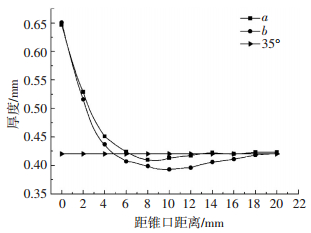
从图 7和8可以看出,试样5和试样6的a点处板料减薄率都比b点的小,减薄范围也减小了.a点与b点相比,只有板料未变形区的长度发生了变化,其他参数一致,说明减小板料未变形区的长度对板料减薄带的产生具有一定的阻碍作用,也间接说明了板料减薄带的产生与板料未变形区有关.
|
图 8 试样6的a点和b点的厚度变化曲线 Figure 8 Thickness curves of point a and b of sample 6 |
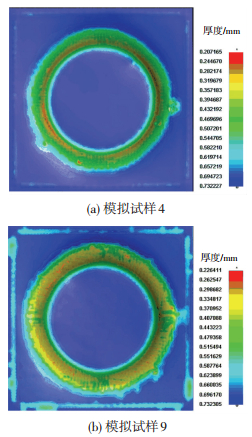
改变板料未变形区的强度也可以对减薄带造成影响,因为减小未变形区板料的强度可以让未变形区的板料下沉更加容易,使板料平缓区域长度增加.本文通过修改未变形区材料A3003铝板应力-应变曲线和降低其初始屈服应力(σs),使板料的强度降低为原来的1/4,其他参数和试样4一致,简称试样9如图 9所示.
|
图 9 不同未变形区板料强度下模拟壁厚分布 Figure 9 Simulated wall thickness distribution with different sheet metal strength of no deformation zone: (a) simulation sample 4;(b) simulation sample 9 |
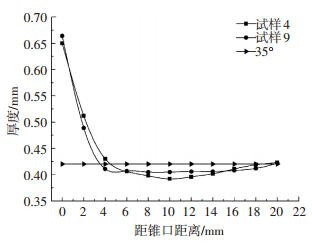
由图 10可以看出,试样9降低了未变形区板料的强度后,板料的减薄带范围增加得较为明显,减薄率下降, 说明试样9的未变形区的板料强度降低导致了板料下沉更加容易,使平缓区域的长度增加,同时板料与工具头之间的作用力因为未变形区板料强度降低会减小,导致工具头对板料的剪切力减小,又因为α变化也相对减慢,使剪切力比较均匀, 所以, 试样9板料在减薄范围增大的同时减薄率下降,且厚度比较均匀,证明板料减薄带的产生受到板料未变形区下沉的影响.
|
图 10 试样4和试样9的厚度变化曲线 Figure 10 Thickness curves of sample 4 and sample 9 |
渐进成形时的板料存在一定的回弹,回弹严重影响了板料的成形精度,因为渐进成形负成形时板料是没有任何模具支撑的,所以目前板料的回弹仍无法避免,高霖等[13]利用有限元软件提出虚拟靠模导向法来修正板料回弹造成的误差.根据已有的文献资料[14]得知, 板料的成形角对变形区回弹的影响较大,板料斜壁与垂直方向的夹角越小,变形区板料的回弹越大,所以, 可以改变成形角来研究板料变形区回弹对减薄带的影响.
由表 1可知,试样7、试样4和试样8的成形角度分别为40°、35°和30°,按板料越来越接近直壁排列,成形工具头直径均为8 mm,垂直进给量均为0.5 mm,板料减薄带壁厚分布如图 11所示.

|
图 11 不同成形角度下的模拟壁厚分布 Figure 11 Simulated wall thickness distribution with different forming angle: (a)simulation sample 7(40°); (b)simulation sample 4(35°); (c)simulation sample 8(30°) |
从图 12可以看出,随着板料成形角度的减小,板料的减薄率和减薄范围都增加得较为明显,且厚度在理论计算值以下的板料部分也相应地增加.可以看出, 增大板料与垂直方向的成形角可以降低板料的减薄率和减薄范围,增大成形角时降低了板料变形区的回弹,也就说明降低板料变形区的回弹可减小板料的减薄率和减薄范围,减小板料的回弹可阻碍减薄带的产生.

|
图 12 试样7、试样4和试样8的厚度变化曲线 Figure 12 Thickness curves of sample 7, sample 4 and sample 8 |
杨氏模量是描述固体材料抵抗形变能力的物理量,衡量的是一个各向同性弹性体的刚度, 定义为在胡克定律的适用范围内单轴应力和单轴形变之间的比[15].板料的回弹是弯曲卸载过程产生的反向弹性变形,回弹的经典计算公式为
| $ \Delta \rho = \frac{M}{{EI}} = \frac{{12M(1-{\nu ^2})}}{{E{t^3}}}. $ | (9) |
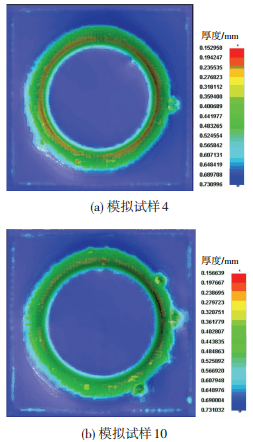
式中:ρ为曲率变化量;M为弯矩;E为杨氏模量;I为弯曲毛坯断面的惯性矩;υ为泊松比;t为回弹前板内的弯矩.由式(9)可以看出,改变杨氏模量可以改变渐进成形中变形区板料的回弹.本实验中板料的杨氏模量增加到原来的3倍,其他参数和试样4一致,简称试样10.减小杨氏模量可以使板料的回弹明显减小,对比试样4和试样10减薄带处厚度变化, 可以分析变形区板料的回弹对减薄带的影响,模拟结果如图 13所示.
|
图 13 不同杨氏模量下的模拟壁厚分布 Figure 13 Simulated wall thickness distribution with different young′s modulus: (a)simulation sample 4;(b)simulation sample 10 |
由图 13可以看到,试样10的板料杨氏模量减小以后,板料锥口处的弹性变形能力降低,工具头挤压时板料受到剪切力的作用容易被穿透,在试样10的表面有3处明显的穿透点.变形区的板料回弹减小以后,减薄带的变化也很明显,减薄率和减薄范围都减小了, 如图 14所示,说明减小变形区板料的回弹可以减小板料的减薄率和减薄范围,减小板料的回弹可以阻碍渐进成形减薄带的产生.

|
图 14 试样4和试样10的厚度变化曲线 Figure 14 Thickness curves of sample 4 and sample 10 |
从图 7~14可以看出,按照渐进成形过程中板料壁厚的正弦定理理论计算[12],成形区域的减薄率是均匀的,但实测和模拟分析的结果显示, 在靠近缘口处,即最初的成形区域厚度较大,而是越往下成形,其减薄率越大,板料壁厚呈现出有规律地不均匀分布.这是因为刚开始渐进成形时平缓区域未变形区板料出现了下沉现象,板料与水平方向的夹角α逐渐增大,成形半锥角θ减小,由文献[7]减薄率
渐进成形工艺中板料减薄带的形成原因一直难以解决,本文根据渐进成形过程中板料轮廓的变化与理想情况下轮廓的区别,对板料减薄带的形成原因进行了推测,认为板料未变形区的下沉和变形区的回弹使板料在初始加工时形成了一段平缓区域,工具头在平缓区域的变形性质发生了变化,发生剪切变形使板料在板料初始加工阶段形成了减薄带,并且对剪切力的变化过程进行了分析.
通过板料未变形区长度和未变形区板料强度渐进成形板料未变形区下沉的影响以及成形角度和杨氏模量对变形区的回弹的影响两个方面对推测的减薄带产生原因进行了数值模拟研究,证明了推测的结论是正确的.
3 结论1) 渐进成形板料产生“减薄带”的原因主要是:板料未变形区的下沉和变形区的回弹使板料在初始加工时形成了一段平缓区域,平缓区域发生剪切变形使板料在初始加工阶段形成了减薄带.
2) 渐进成形时,减小板料未变形区的长度、增大板料与垂直方向的角度可以在一定程度上阻碍减薄带的产生.
3) 可以利用传统成形的局部成形理论对渐进成形板料减薄范围进行理论计算,计算结果对于观察不同的加工参数对减薄范围的影响具有重要的借鉴意义.
| [1] | SURESH K, SRINIVASA P R. Experimental and numerical studies on formability of extra-deep drawing steel in incremental sheet metal forming[J]. Journal of Materials Research and Technology, 2014, 3(2): 158–171. DOI: 10.1016/j.jmrt.2014.03.009 |
| [2] | TEGAN M, JACK J, MATHEW D. Formability in single point incremental forming: a comparative analysis of the state of the art[J]. CIRP Journal of Manufacturing Science and Technology, 2017, 16: 43–54. DOI: 10.1016/j.cirpj.2016.07.003 |
| [3] | AMAR K B, RICARDO A D S, GIUSEPPE I, et al. Single point incremental forming: an assessment of the progress and technology trends from 2005 to 2015[J]. Journal of Manufacturing Processes, 2017, 27: 37–62. DOI: 10.1016/j.jmapro.2017.03.014 |
| [4] | ERIKA S, JAEKWANG S, MAYA N, et al. Investigation of thickness variation in single point incremental forming[J]. Procedia Manufacturing, 2016, 5: 828–837. DOI: 10.1016/j.promfg.2016.08.068 |
| [5] |
蔡改贫, 周小磊, 熊洋, 等. 工艺参数对多点复合渐进成形厚度减薄的影响[J]. 材料科学与工艺, 2015, 23(4): 59–63.
CAI Gaipin, ZHOU Xiaolei, XIONG Yang, et al. Impacts of multi-point incremental forming process parameters on plate thickness thinning[J]. Materials Science and Technology, 2015, 23(4): 59–63. DOI: 10.11951/j.issn.1005-0299.20150410 |
| [6] | MOHAMMAD J M, MOHSEN S. Numerical prediction of failure in single point incremental forming using a phenomenological ductile fracture criterion[J]. Journal of Materials Processing Technology, 2017, 244: 17–43. DOI: 10.1016/j.jmatprotec.2017.01.029 |
| [7] | 周六如. 金属板料数控渐进成形机理及工艺的研究[D]. 武汉: 华中科技大学, 2004. |
| [8] | HUSSAIN G, HAYAT N, GAO L. An experimental study on the effect of thinning band on the sheet formability in negative incremental forming[J]. International Journal of Machine Tools and Manufacture, 2008, 48: 1170–1178. DOI: 10.1016/j.ijmachtools.2008.02.003 |
| [9] | MARTINS P A F, BAY N, SKJOEDT M, et al. Theory of single point incremental forming[J]. CIRP Annals-Manufacturing Technology, 2008, 57: 247–252. DOI: 10.1016/j.cirp.2008.03.047 |
| [10] | LI Junchao, HU Jianbiao, GENG Panpei. Thickness distribution and design of a multi-stage process for sheet metal incremental forming[J]. Journal of Materials Processing Technology, 2012, 62: 981–988. |
| [11] | HUSSAIN G, HAYAT N, GAO L. A comparative study on the forming limits of an aluminum sheet-metal in negative incremental forming metal in negative incremental forming[J]. Journal of Materials Processing Technology, 2007, 187-188: 94–98. DOI: 10.1016/j.jmatprotec.2006.11.112 |
| [12] |
王华毕, 桑文刚, 魏目青. 金属板料单点渐进成形性能的研究[J]. 机械设计与制造, 2017(1): 108–111.
WANG Huabi, SANG Wengang, WEI Muqing. Research of sheet metal based on single point incremental formability[J]. Machinery Design and Manufacture, 2017(1): 108–111. DOI: 10.19356/j.cnki.1001-3997.2017.01.029 |
| [13] |
李泷杲, 高霖, 韦红余. 金属板料渐进成形有限元仿真过程中复杂成形路径的构建方法[J]. 机械工程学报, 2006, 42(6): 227–230.
LI Shuanggao, GAO Lin, WEI Hongyu. Method on generating complex loading path for FEM simulation of incremental sheet metal forming process[J]. Journal of Mechanical Engineering, 2006, 42(6): 227–230. |
| [14] | RAUJOL-VEILLÉ J, TOUSSAINT F, TABOUROT L, et al. Experimental and numerical investigation of a short, thin-walled steel tube incremental forming process[J]. Journal of Manufacturing Processes, 2015, 19: 59–66. DOI: 10.1016/j.jmapro.2015.03.008 |
| [15] |
马丽霞, 孙红磊, 殷璟, 等. 板材杨氏模量对称三点弯曲测试方法及测试装置[J]. 塑性工程学报, 2011, 18(5): 95–98.
MA Lixia, SUN Honglei, YIN Jing, et al. Symmetric 3-point bending test method and device for Young's modulus of sheet metal[J]. Journal of Plasticity Engineering, 2011, 18(5): 95–98. |
 2018, Vol. 26
2018, Vol. 26


