2. 中国科学院 金属研究所,沈阳 110016
2. Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China
由于Al基金属玻璃具有超高的强度和优异的耐蚀性,有望在工程材料上获得广泛应用.然而,截止目前,最大的铝基金属玻璃直径仅有2.5 mm[1-3],这是目前能够形成非晶体系中形成能力最差的体系,如此低的玻璃形成能力极大地制约其应用,因此,提高铝基金属玻璃的形成能力,获得大尺寸块体金属玻璃,是实现其工程化应用的前提条件.
最近,研究人员已经提出许多有关玻璃形成能力的热力学判据[4]和理论模型[5-6],目的都是解决玻璃形成能力这一难题.众所周知,著名的热力学判据—约化玻璃转变温度(Trg),它与玻璃形成能力密切相关,但是,对于Al-TM-RE三元合金体系,其玻璃形成能力却背离Trg判据.玻璃形成能力从本质上是由原子结构决定的,为此,Miracle等人提出了有效密排团簇模型(ECP) model[5],可有效地预测大部分的强玻璃形成能力体系,但是用于Al基金属玻璃合金设计,其成分预测偏差较大,其根本原因是ECP模型仅仅考虑了原子之间的拓扑结构特点,忽略了原子之间化学作用对整个非晶结构稳定性的影响,而对于Al基金属玻璃,其原子之间的化学作用(例如:Al和TM)对结构稳定性起到很大作用,所以该模型失效.在此之后,在ECP模型的基础上,针对Al基金属玻璃的特殊性,提出了有效原子密排化学耦合模型[7-8].此外,利用第一性原理和反蒙特卡洛分子动力学的模拟[9], Sheng和Shi系统研究了Al-Ni-La、Al-Y-La和Al-Ni-Y-La金属玻璃中原子排列结构的差异[10-11].然而,以上这些原子结构模型和计算机模拟都是从原子角度研究玻璃形成能力与合金成分的强烈相关性,却不能揭示RE元素和TM元素对影响Al-TM-RE三元合金体系玻璃形成能力的本质.我们假想是否可以从原子结构角度深入到电子结构角度去揭示RE元素和TM元素对影响Al-TM-RE三元合金体系玻璃形成能力的本质,也就是说,是否可以从电子结构变化角度去解释玻璃形成能力对元素敏感性影响的本质.
有关金属玻璃电子结构对结构稳定性的影响很早就有研究者研究.对于没有含TM元素的金属玻璃,从头计算方法的赝势方法用于计算原子之间的相互作用.Hafner[12]建立了金属间化合物拓扑紧密排列的形成和玻璃形成之间的关系,而对于含有TM原子的金属玻璃(例如:Al-TM-RE),由于Al原子和TM原子之间强烈轨道杂化效应的影响,Hafner提出的方法失效.此外, Nagel和Tauc [13]在费米面和伪布里渊区作用机制的基础上体提出了金属玻璃的Hume-Rothery稳定机制,其基本思想是:在倒易空间中,费米面的直径为2KF,伪布里渊区的直径是KP,当两者相切的时候,也就是2KF=KP,金属玻璃结构稳定性增强,费米能级处的电子态密度达到最低,体系能量最低,结构最稳定.该理论用于Al-TM-RE合金体系,sp-d电子轨道杂化效应对费米面尺寸(2KF)有很大影响,这种作用的影响类似于上面所说的同时含有TM元素和非过渡族元素的化合物.也就是说,虽然Al和TM之间轨道杂化效应的存在,但这种费米面和伪布里渊区相互作用机制仍然适用.同时,伪布里渊区的尺寸(KP)主要是由Al和RE之间的静态原子结构决定.这表明在Al-TM-RE三元合金体系中TM原子和RE原子对玻璃形成能力的影响可以通过比较2KF和KP的大小定量表征.
本文的研究目的就是从电子结构稳定性角度,探究Ni原子和Y原子对Al-Ni-Y三元金属玻璃的玻璃形成能力影响的本征机理.在Al基三元合金体系中,Al-Ni-Y合金是玻璃形成能力最强的体系[8, 13-14].Ni元素作用是调节电子轨道杂化效应,改变费米面的大小;Y元素作用是改变静态结构,改变伪布里渊区的尺寸.KF和KP通过电子能量损失谱(EELS)、X射线衍射(XRD)和X射线光电子能谱(XPS)间接得到.KP和2KF接近程度决定了Al-Ni-Y合金的玻璃形成能力的强弱.
1 Al-Ni-Y三元合金体系中费米面和伪布里渊区相互作用机制非晶合金的形成和结构的稳定性都是由电子系统和静态原子系统相互耦合而产生的球周期共振所决定的.在电子系统中,产生的费米面,其大小(2KF)由近自由电子模型决定,具体表达式如下[16]:
| $ 2{K_F} = 2\sqrt[3]{{3{{\rm{ \mathsf{ π} }}^2}{n_0}Z.}} $ | (1) |
其中,n0代表平均原子数密度,Z代表平均价电子数.对于Al-Ni-Y玻璃形成体系,Al-3p态和Ni-3d态之间存在强烈的电子轨道杂化效应,这将会降低体系的传导电子态密度,影响费米面和伪布里渊区相互作用.在这种情况下,真实的电子态密度将背离近自由电子模型(公式(1)不适用),此时,总的电子态密度可以分成两部分,一部分是自由电子(ZFEM)的贡献,另一部分是Al-3P和Ni-3d之间杂化电子(Zhyb)的贡献,2KF可以写成[17]:
| $ \begin{array}{l} 2{K_{\rm{F}}} = 2K_{\rm{F}}^{{\rm{FEM}}} - 2K_{\rm{F}}^{{\rm{hyb}}} = 2\sqrt[3]{{3{{\rm{ \mathsf{ π} }}^2}{n_0}{Z_{{\rm{FEM}}}}}} - \\ \;\;\;\;\;\;\;\;\;\;\; 2{\sqrt[{3}]{{3{{\rm{ \mathsf{ π} }}^2{n_0}Z}}_{{\rm{hyb}}}}.} \end{array} $ | (2) |
式中:2KFFEM和2KFhyb分别是由自由电子模型和杂化模型计算得到的,ZFEM是在自由电子模型中的平均价电子数,Zhyb是转移的价电子数.其中,原子数密度(n0)由下式决定:n0=ρNAv/M,ρ是金属玻璃的质量密度,M是摩尔质量,NAv是阿伏伽德罗常数.
伪布里渊区尺寸(KP)表征静态原子结构特性, KP值可以利用X射线衍射图像中伪布拉格峰的位置(非晶合金中的“馒头峰”)获得,其关系式为
| $ {K_{\rm{P}}} = \frac{{4{\rm{ \mathsf{ π} sin}}\theta }}{\lambda }. $ | (3) |
其中,X射线的波长λ=0.1542 nm,θ是谱线中主峰(馒头峰)的峰位.
在K空间(实空间)中,当满足KP= 2KF时,整体结构达到理想共振态,代表两个系统(电子系统和静态原子系统)相互耦合,达到平衡状态,最终导致费米能级初电子态密度达到最低[15].
下面我们考虑在三元合金体系中,Ni原子和Y原子对费米面和伪布里渊区的影响.通常分为两种:一种是Al-Ni-Y中Ni原子的影响,Al-3p和Ni-3d之间电子轨道杂化,其改变了3d轨道的有效电子数,最终导致费米面尺寸(KF)变化;另一种是Al-Ni-Y中Y原子的影响,Y原子和Al原子之间不存在电子轨道杂化效应,而Y原子半径在体系中最大,且远大于Al主元的原子半径,因此,Y原子通过改变静态原子结构来改变伪布里渊区的大小(KP).综上所述,为了定量化Ni原子和Y原子对玻璃形成能力的影响,我们提出了电子结构判据,δ=|KP-2KF|.
在下文中,我们从实验上确定KP和2KF的值.利用公式(2)可以得出KF,公式中的各个参量可以用电子能量损失谱和X射线光电子能谱实现定性和定量化表征.KP的值可以通过X射线衍射,利用公式(3)求得.为了进一步衡量费米能级出电子态密度的影响,利用综合物性测量系统(PPMS)和XPS价带谱测量不同合金成分的低温比热,获得低温电子比热系数(γ)的值,通过低温电子比热系数可以间接反映费米能级处电子态密度的大小.
2 实验 2.1 材料和样品的制备电弧熔炼法制备Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)母合金.原始材料(Al、Ni、Y)的纯度高于99.9%,按照原子百分比配比,在Edmund Bühler(Compact Arc Melter MAM-1)中真空电弧炉制备.电弧熔炼炉采用水冷铜坩埚,Ti球吸收气氛中的氧气及其他杂质,用来纯化保护气体.通过单辊熔体急冷法,在高纯氩气制备合金条带样品,条带的截面尺寸为(0.03-0.05)m×3 mm.楔形样品在真空单辊熔体急冷设备上制备,模具的楔倾角为5°,压差为400~800 MPa,样品质量大约3 g.
2.2 样品的表征X射线衍射(XRD)分析是在Rigaku D/max2400衍射仪(日本东京生产)上进行,采用Cu Kα射线源(λ=0.154 2 nm).楔形样品取其尖端完全非晶部分,利用综合物性测量系统(PPMS-9000 Physical Property Measurement System)测量样品的低温比热(CP).X射线光电子能谱(XPS)实验在ESCALAB250能谱仪上进行,采用Al靶作为X射线源,对应Al Kα激发能量为 hν=1 486.6 eV,金属玻璃薄带样品经过一系列型号砂纸打磨后,然后用2000#砂纸精心打磨,表面再采用Ar离子进行短时间的溅射,溅射到C 1s和O 1s信号的峰达到最小,溅射的电压是4 keV.由于离子溅射束的尺寸为2 mm, 速率为0.2 nm/min, 在室温下溅射时间仅仅几秒钟,因此在这种条件下不会使合金样品发生晶化.结合能用C 1s峰(284.6 eV)进行校准,采用阿基米德方法测量金属薄带样品的密度.
使用带有GATAN附件的日本生产JEOL JEM-2010型透射电子显微镜(TEM)进行电子能量损失谱的测量,由于离子减薄样品容易发生晶化,TEM观察中所用的电镜样品采用双喷电解抛光法制得,电解液是20vol.%硝酸甲醇溶液.双喷的电流和电压分别是46 mA和8 V,双喷温度是-35 ℃.采集EELS谱时电镜处于衍射模式,能量发散度是0.2 eV/channel,相机长度是8 cm,接收光阑边长是3 mm,能量分辨率是1.4 eV,每个试样在相似的厚度随机采集Ni的EELS谱数量为10个,所有的谱扣除本底后都采用Fourier-ratio方法解卷积以去除多重散射的影响.
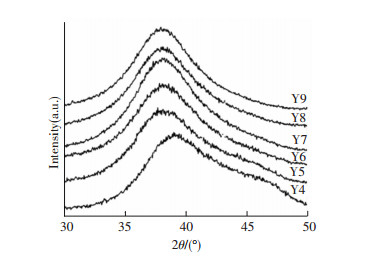
3 结果和讨论 3.1 Al86Ni14-xYx(x=4, 5, 6, 7, 8, 9 at.%)合金中的电子结构判据图 1是Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的楔形样品的X射线衍射结果,由图可以看出,随着Y元素含量的增加,主峰的峰位随之降低.利用公式(3)我们可以得出Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金中随着Y元素含量的增加,其KP值的变化,具体结果见表 1.
|
图 1 Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的楔形样品的XRD结果 Figure 1 XRD patterns of the Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%) wedge-shaped sample |
| 表 1 Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的Y 3d、Al 2p1/2和Ni 2p3/2结合能和纯Y、Al和Ni的化学位移,分别用ΔBEY 3d、ΔBEAl2p1/2和ΔBENi2p3/2表示 Table 1 Binding energy variations for Y 3d, Al2p1/2, and Ni2p3/2 between pure element and the Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%) alloys, referred to as ΔBEY3d, ΔBEAl2p1/2, and ΔBENi2p3/2, respectively |
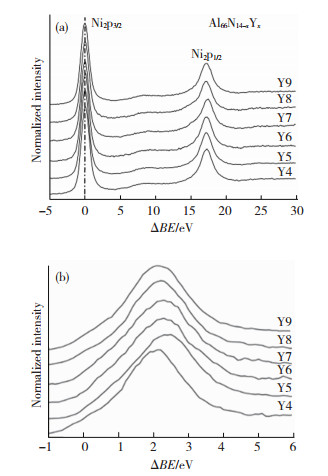
费米面尺寸(KF)与Al原子和Ni原子之间的电子杂化作用密切相关,对于Al86Ni14-xYx(x=4, 5, 6, 7, 8, 9 at.%)合金,不同的Ni含量影响电子轨道杂化作用的强弱.为了表征这种电子杂化效应,我们利用XPS测量了Al86Ni14-xYx(x=4, 5, 6, 7, 8, 9 at.%)合金中Al、Ni、Y三种元素的化学位移,其结果见表 1.表 1给出了合金中Al、Ni、Y的结合能和单质态的Al、Ni、Y结合能的差值,很明显地看出,合金中Al2p1/2原子结合能比纯金属Al2p1/2的结合能要低,其化学位移大约0.3 eV, ΔBEAl2p1/2=-0.3 eV,与之正好相反的是,合金中Ni2p3/2原子结合能比纯金属Ni2p3/2的结合能要高,ΔBENi2p3/2=0.3 eV,其化学位移大约0.3 eV.由于高的静电能的存在,这种化学位移产生的本质不是真实地电荷的转移,而是Al-3p态上的电子“填加”到的Ni-3d空态.此外,我们还发现Y 3d不存在化学位移的变化,ΔBEY 3d=0,这说明在Al86Ni14-xYx(x=4, 5, 6, 7, 8, 9 at.%)合金中,无论合金成分如何变化,Al原子和Y原子之间没有发生电荷的转移.以上电子之间转移效应其他研究者在同步辐射X射线实验中也得到证实.图 2(a)展示了Al86Ni14-xYx(x=4, 5, 6, 7, 8, 9 at.%)合金中Ni2p3/2主峰及其卫星峰的测量结果,由图可知,随着合金中Y元素含量的增加,其卫星峰的强度降低,并且卫星峰位置逐渐地偏离Ni2p3/2主峰,也就是卫星峰和主峰之间的距离(ΔEsat)增大.表 1给出了Ni2p3/2卫星峰强度和不对称指数的变化,在这里,Ni2p3/2卫星峰的强度是由费米能级以上的未占据态的3d轨道特征所决定.此外,Ni主峰的不对称指数的变化也密切反映了d态电子的变化情况,所以随着Y含量的增加,Ni2p3/2不对称指数与Al原子和Ni原子之间转移的电荷数的减少有及其密切的关系.
|
图 2 Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的(a)Ni2p3/2和Ni2p1/2,(b)XPS价电子能谱 Figure 2 (a) Ni2p3/2 and Ni2p1/2 XPS spectra, (b) XPS valence band spectra for the Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%) alloys |
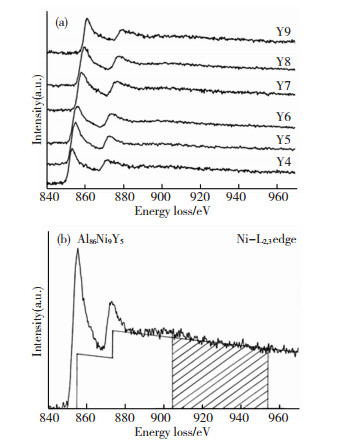
为了定量地表征电子轨道杂化导致的电子转移信息,我们进一步地测量了Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金中Ni L2和L3的白线峰,结果如图 3(a)所示.对于含有3d未占据的态密度的过渡族金属,白线峰将会反映过渡族金属的电子从2p态转移到3d态的信息.原子态为2p63d(m)2p,电子受激发一个电子后,变成2p53d(m+1),其中m代表3d占据态密度的电子数,Ni L3 and L2白线峰分别对应2p3/2转变成3d3/23d5/2以及2p1/2转变成3d3/2,其峰强度与3d电子未占据态密度有关,因此,过渡族元素最外层d态电子的转移可以通过检测白线峰获得.Pearson等人推论出归一化白线峰的积分强度(L2和L3峰强度之和)和与d电子占据态密度存在线性关系,最终反映d态电子填充状态.因此,白线峰积分强度的变化能够直接关系到d态电子数(电荷转移).L2和L3白线峰采用Pearson的双阶跃函数扣除本底的方法,见图 3(b),其具体步骤如下:首先,对Ni L2峰后大约50 eV范围内的谱线进行直线拟合, 再将拟合的直线延长至Ni L2峰的最高值位置, 之后,该直线再垂直下降的高度为h1, 再用相同斜率的直线延伸至L3峰的最高值位置,随后再垂直下降至0, 下降的高度为h2, 两次下降的高度h1和h2之比为1:2.两条直线下面的面积就是本底, 对L2和L3峰进行本底的扣除, 得到白线强度;其次,以Ni L3峰最高值往后50 eV为起点, 向后50 eV这一段谱线的积分面积作为归一化窗口, 即图中所示阴影部分.将扣除本底后的白线的积分面积进行归一化处理, 得到归一化的白线强度,得到的谱线才能用来定量分析.最后,利用归一化白线强度与d电子占据态密度的函数关系,得到合金中Ni的3d占据态密度[22]:
| $ I = 1.06\left( {1 - 0.094n} \right). $ | (4) |
|
图 3 Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的(a)EELS测量的Ni-L2, 3白线峰,(b)对Al86Ni9Y5合金的Ni-L2, 3白线峰进行处理的过程 Figure 3 (a) Ni-L2, 3 edge EELS spectra for Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%) amorphous alloys, (b) method for isolating and normalizing the white-line intensities for the Ni-L2, 3 edge for the Al86Ni9Y5 alloy |
其中I是归一化的白线峰强度,n是每个原子的Ni 3d轨道的电子数.利用测量的归一化后的白线峰强度,根据公式(4)求得了n值,Ni 3d轨道的电子数(n)计算结果见表 2,测量得到的Ni原子中3d轨道电子数的变化证实了电子从Al原子转移到外层的Ni 3d轨道上,这和XPS测量的化学位移的结果相一致.
| 表 2 由EELS测量得到的Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的电子轨道杂化信息 Table 2 Electronic hybridization information obtained from the EELS for the Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%) alloys |
下面计算Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)非晶合金的KF值.首先,我们知道Z(Ni)=2, Z(Al)=3, Z(Y)=3, KFFEM和KFhyb值由式(2)求得.在公式(2)中,自由电子的价电子浓度,ZFEM是所有合金元素(Al、Ni、Y)的自由电子共同贡献的结果,其关系式是:ZFEM=∑iCiZi,其中Ci和Zi分别表示i元素的原子百分比含量和自由电子浓度,Zhyb由以下公式得出:Zhyb=C(n-n3d), 其中,n和n3d分别代表每个Ni原子的Al-Ni-Y的3d电子数和纯金属Y的3d电子数,n的值由公式(4)计算获得,其结果见表 1.随着Ni含量的变化,KF值的变化也在表 1中给出.
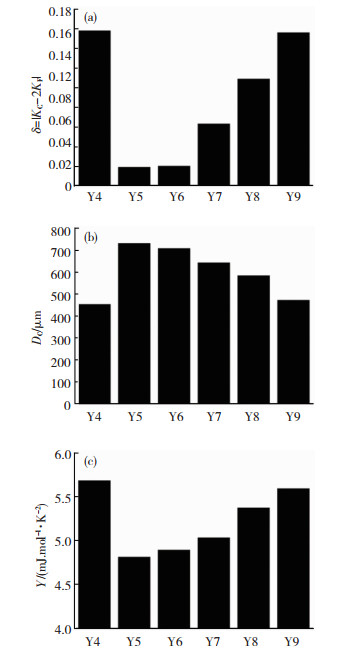
最后,计算了Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金成分的电子结构判据,δ=|Kp-2KF|,其结果见图 4(a), 从图中可以看出,在所有合金成分中,Al86Ni9Y5 合金的δ值最小,因此,预测该合金成分的玻璃形成能力最强.
|
图 4 Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)的(a)δ=|Kp-2KF|,(b)临界玻璃形成尺寸(Dc),(c)低温电子比热系数(γ) Figure 4 (a)δ=|Kp-2KF|, (b) Critical thickness for glass formation, Dc, and (c) the electronic specific heat coefficient (γ) value for the Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%) alloys |
图 1表示Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的楔形样品尖端部分X射线衍射结果图,图中没有观察到晶体峰,其表现出典型的“馒头峰”的特征,这说明所有合金成分都是完全非晶.图 4(a)和4(b)分别表示Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金中δ值和临界玻璃形成能力(Dc)之间的关系,由图可以得出以下规律:δ值越小,合金的玻璃形成能力越强,这种玻璃形成能力的变化趋势和之前提出的模型预测的完全一致.在Al-Ni-Y三元体系中, Al86Ni9Y5合金的玻璃形成能力最强,其成分对应的δ值最小.Al-Ni-Y三元金属玻璃体系中,这种玻璃形成能力和δ值的对应关系表明电子结构判据在预测玻璃形成能力的有效性.
以上预测的Al-Ni-Y金属玻璃中玻璃形成能力最强的成分,其费米能级初的电子态密度最低,也就是说玻璃形成能力最强的合金成分,在费米面处具有最低的电子态密度.为了证明以上的推论,我们测量了Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金的费米能级处电子态密度值(N(EF)),众所周知,低温电子比热系数(γ)和N(EF)的直接关系式如下:
| $ \gamma = (\frac{{{{\rm{ \mathsf{ π} }}^2}}}{3})k_{\rm{B}}^2{\rm{N}}({E_{\rm{F}}}). $ | (5) |
其中,kB是玻尔兹曼常数.从本质上说,低温电子比热系数(γ)可以反映费米能级处电子态密度(N(EF))的大小.γ值达到最小,也就是N(EF)最低时,对应着非晶“能带结构”中的“伪能隙”.为了方便比较,图 4(c)表示出不同Al86Ni14-xYx (x=4, 5, 6, 7, 8, 9 at.%)合金成分中γ值的变化规律,明显地看出,玻璃形成能力最强的合金(Al86Ni9Y5),其低温电子比热系数值在所研究的合金成分中最小,此外,XPS价电子能谱的结果(图 2(b))也间接反应了不同合金成分的费米能级处电子态密度(N(EF))大小.因此,玻璃形成能力和低温电子比热系数之间的关系直接验证了电子结构判据(费米面和伪布里渊区相互作用机制)在控制非晶结构方面的有效性,更重要的是,揭示了Al-Ni-Y三元金属玻璃的玻璃形成能力受Ni原子和Y原子影响的本征机理.
4 结论根据金属玻璃的费米面和伪布里渊区理论,揭示了Ni原子和Y原子对Al-Ni-Y三元金属玻璃体系玻璃形成能力影响的本质.Al原子和Y原子之间的静态结构的改变影响伪布里渊区(KP)的尺寸;Al原子和Ni原子之间的电子轨道杂化效应的改变影响费米面(2KF)的大小.也就是说,当两者影响的相互作用机制满足2KF=KP, 条件时,费米能级处电子态密度最低,金属玻璃整体结构的稳定性得到加强.其中,费米面(2KF)和伪布里渊区(KP)通过XPS、EELS、XRD和PPMS实验手段获得.并且在此基础上,提出了δ=|KP-2KF|判据来定量地表征Ni原子和Y原子对玻璃形成能力的影响.
| [1] | WU N C, ZUO L, WANG J Q, et al. Designing aluminum-rich bulk metallic glasses via electronic-structure-guided microalloying[J]. Acta Mater, 2016, 108: 143–151. DOI: 10.1016/j.actamat.2016.02.012 |
| [2] | SHEN Y, PEREPEZKO J H. Al-based amorphous alloys: glass-forming ability, crystallization behavior and effects of minor alloying additions[J]. J Alloys Compd, 2017, 707: 3–11. DOI: 10.1016/j.jallcom.2016.11.079 |
| [3] | YANG B J, LU W Y, ZHANG J L, et al. Melt fluxing to elevate the forming ability of Al-based bulk metallic glasses[J]. Scientific Reports, 2017, 1: 1105301–110516. |
| [4] | TURNBULL D. Under what condition can a glass be formed[J]. Cont. Phys, 1969, 10(5): 473–488. DOI: 10.1080/00107516908204405 |
| [5] | MIRACLE D B. A structural model for metallic glasses[J]. Nat Mater, 2004, 3: 697–702. DOI: 10.1038/nmat1219 |
| [6] | WU Z W, LI M Z, WANG W H, et al. Hidden topological order and its correlation with glass-forming ability in metallic glasses[J]. Nat Commun, 2015, 6: 60351–60357. |
| [7] | INOUE A, OHTERA K, ZHANG T, et al. Effect of intense rolling and folding on the phase stability of amorphous Al-Y-Fe alloys[J]. Jpn J Appl Phys, 1988, 27: 479(8)–482. |
| [8] | WU N C, KAN D, ZUO L, et al. Efficient atomic packing-chemistry coupled model and glass formation in ternary Al-based metallic glasses[J]. Intermetallics, 2013, 39: 1–4. DOI: 10.1016/j.intermet.2013.03.008 |
| [9] | KIM W, OH H S, PARK E S. Manipulation of thermal and mechanical stability by addition of multiple equiatomic rare-earth elements in Al-TM-RE metallic glasses[J]. Intermetallics, 2017, 91: 8–15. DOI: 10.1016/j.intermet.2017.07.019 |
| [10] | SHENG H W, CHENG Y Q, LEE P L, et al. Atomic packing in multicomponent aluminum-based metallic glasses[J]. Acta Mater, 2008, 56: 6264–6272. DOI: 10.1016/j.actamat.2008.08.049 |
| [11] | SHI X M, WANG X D, YU Q, et al. Structure alterations in Al-Y-based metallic glasses with La and Ni addition[J]. J Appl Phys, 2016, 119: 1149041–1149049. |
| [12] | HAFNER J, HEIMENDAHL L V. Microscopic calculations of the stability of metallic glasses[J]. Phys. Rev. Lett., 1979, 42(6): 386–389. DOI: 10.1103/PhysRevLett.42.386 |
| [13] | WANG Q, LI J H, LIU J B, et al. Atomistic design of favored compositions for synthesizing the Al-Ni-Y metallic glasses[J]. Sci Rep, 2015, 5: 16218. DOI: 10.1038/srep16218 |
| [14] | WU N C, LIAN J B, WANG R, LI R H, et al. Effect of element types on the glass forming ability of Al-TM-RE ternary metallic glasses using electron structure guiding[J]. J Alloys Compd, 2017, 723: 123–128. DOI: 10.1016/j.jallcom.2017.06.262 |
| [15] | NAGEL S R, TAUC J. Nearly-free-electron approach to the theory of metallic glass alloys[J]. Phys Rev Lett, 1975, 35(6): 380–383. DOI: 10.1103/PhysRevLett.35.380 |
| [16] | STIEHLER M, GIEGENGACK J, BARZOLA-QUIQUIA J, et al. Peculiarities in the plasma resonance of binary amorphous Al-TM alloys[J]. Journal of Physics Chemistry of Solids, 2007, 68(5-6): 1244–1248. DOI: 10.1016/j.jpcs.2006.12.020 |
 2018, Vol. 26
2018, Vol. 26


