2. 空军航空大学 飞行训练基地,辽宁 锦州 121000
2. Air Force University Aviation Training Base, Jinzhou 121000, China
飞机钣金制造过程中,框肋类零件具有种类多、批量小、精度要求高等特点.采用传统的制造方法无法满足航空工厂的要求.橡皮成形工艺是利用橡皮作为弹性凹模(凸模),用液体作为传压介质使金属板料随刚性凸模(凹模)变形的一种软模成形方法[1-2].橡皮成形工艺在现代飞机制造过程中占50%以上,提高了零件成形质量和结构的可靠性,使成形零件可不经修整或少量修整便可直接用于装配.
钣金零件成形过程中回弹量是获得所需零件几何形状和相应模具设计的重要参数,近年来板料成形领域对回弹补偿技术进行了大量的研究.Livatyali和Altan [3]提出了一种计算机辅助设计方法,使用有限元方法对直弯边零件进行回弹补偿;Nanu和Brabie[4]分析了U型弯曲工艺参数对回弹的影响,并得出回弹参数是板料厚度应力分布的函数;Wagoner等.[5]对纯弯曲变形卸载前所加弯曲力矩的计算进行推导,得出相对弯曲半径越小,弯曲力矩越大.孙志英等[6]利用Hill理论分析了液压成形过程中应力分布对回弹的影响.裴兴林等[7]用正交试验设计法和均匀试验设计法对L型薄板弯曲回弹进行预测,得出厚向积分点数对回弹影响非常显著;阳湘安等[8]提出了一种基于多目标优化的综合评判回弹方法,建立了分别以等效应力偏差和等效塑性应变来表征目标函数,表明了方法的有效性;陈磊等[9]采用正交试验方法分析了不同因素对凹弯边回弹的影响,得出增大模具圆角半径,回弹增加,增加翻边高度,回弹先降低后增大.
上述回弹研究主要针对刚性模具,对于橡皮成形回弹补偿的理论研究和补偿系统的开发还不足,本文提出补偿因子对回弹公式进行修正,并通过CATIA二次开发对模具进行补偿,利用数值模拟对直弯边下陷零件橡皮成形回弹补偿进行研究.
1 板料回弹理论公式 1.1 回弹公式板料在成形过程中,当卸载之后弹性变形消失,板料变形区由于残余应力释放将导致零件发生回弹现象,板料在弯曲成形时模型如图 1所示[10-11].
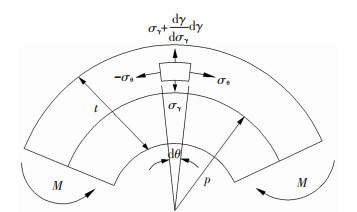
|
图 1 板料弯曲成形分析模型 Figure 1 Sheet bending forming analysis model |
根据塑性力学知识,在平面应变情况下的屈服条件为
| $ {\sigma _{\rm{ \mathsf{ θ} }}} - {\sigma _{\rm{r}}} = \pm \frac{{1 + r}}{{\sqrt {1 + 2r} }}\overline \sigma . $ | (1) |
式中:σθ, σr分别为切向、厚向的应力,r为厚向异性系数,
| $ \Delta {\varepsilon _\theta } = \frac{\eta }{\rho } - \frac{\eta }{{{\rho ^*}}}. $ | (2) |
式中:ρ为卸载前曲率半径,ρ*为卸载后曲率半径.为了简化模型,卸载时产生的弯矩为
| $ \Delta M = 2b\int_0^{\frac{t}{2}} {\Delta {\varepsilon _\theta }\eta {\rm{d}}\eta = \frac{{bE{t^3}}}{{12(1 - {\nu ^2})}}(\frac{1}{\rho } - \frac{1}{{{\rho ^*}}}).} $ | (3) |
式中:E为弹性模量,t为板料厚度,ν为泊松比,卸载完成时弯矩为
| $ M = K{\left( {\frac{{1 + r}}{{\sqrt {1 + 2r} }}} \right)^{1 + n}}\frac{{b{t^2}}}{{4\left( {1 + n} \right)}}{\left( {\frac{t}{{2\rho }}} \right)^n}. $ | (4) |
式中:K为强化系数,n为应变强化指数,根据卸载前后弯矩大小相等,方向相反,即ΔM=M,可推导出
| $ \Delta \theta = \frac{1}{\rho } - \frac{1}{{{\rho ^*}}} = K{\left( {\frac{{1 + r}}{{\sqrt {1 + 2r} }}} \right)^{1 + n}}\frac{{3(1 - {\nu ^2})}}{{Et\left( {1 + n} \right)}}{\left( {\frac{t}{{2\rho }}} \right)^n}. $ | (5) |
由于板料回弹前后中性层长度不变即ρθ=ρ*θ*,可以得出回弹角Δθ和回弹后圆角半径ρ*分别为
| $ \Delta \theta = K{\left( {\frac{{1 + r}}{{\sqrt {1 + 2r} }}} \right)^{1 + n}}\frac{{3(1 - {\nu ^2})}}{{2E\left( {1 + n} \right)}}{\left( {\frac{t}{{2\rho }}} \right)^{n - 1}}\theta , $ | (6) |
| $ {\rho ^*} = \frac{{\rho \theta }}{{\theta - \Delta \theta }}. $ | (7) |
在飞机设计过程中,钣金零件结构特征存在较多的下陷,典型直弯边下陷零件如图 2所示.下陷的主要目的是起到躲避其他零件的作用.

|
图 2 典型直弯边下陷零件 Figure 2 Typical straight jogged parts |
下陷区截面示意图如图 3所示,下陷区与两侧弯边结合位置有一段过渡圆角半径区,在成形时,此区域的应力分布比较复杂,为了方便计算弯矩,忽略过渡圆角半径区域的应力计算,将下陷区域简化.
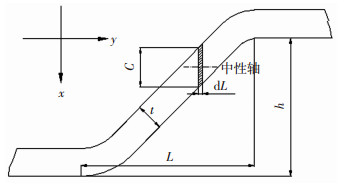
|
图 3 下陷区截面示意图 Figure 3 Section diagram of the jogged zone |
下陷区弯矩与纯弯曲产生弯矩计算类似,其大小为
| $ {M_2} = K{\left( {\frac{{1 + r}}{{\sqrt {1 + 2r} }}} \right)^{1 + n}}\frac{{\sqrt {{L^2} + {h^2}} {t^2}{{\left( {\frac{t}{{2\rho }}} \right)}^n}}}{{4\left( {1 + n} \right)}}. $ | (8) |
方向垂直于下陷区中性面,其中
下陷区卸载后的弯矩ΔM2可分解为两个方向上的弯矩ΔM2x和ΔM2y,其中ΔM2x是下陷区卸载后产生回弹的弯矩,ΔM2y在卸载后变成残余应力贮存在板料中,对回弹没有产生影响.因此用于产生回弹的弯矩为
| $ \Delta {M_2} = \frac{L}{{\sqrt {{L^2} + {h^2}} }}{M_2}. $ | (9) |
沿Y方向将下陷区分成无数个宽度为dL的微元,由几何关系可以确定微元的长度c,其表达式为
| $ c = \frac{{t\sqrt {{L^2} + {h^2}} }}{L}. $ | (10) |
根据材料力学矩形截面惯性矩计算公式得出每个微元的惯性矩为
| $ {\rm{d}}L = \frac{{\left( {\frac{{t\sqrt {{L^2} + {h^2}} }}{L}} \right){\rm{d}}L}}{{12}} $ | (11) |
则整个下陷区的惯性矩为
| $ {I^j} = \int_0^L {{\rm{d}}I = \frac{{\left( {t\sqrt {{L^2} + {h^2}} } \right)}}{{12{L^2}}}.} $ | (12) |
下陷区影响着下陷区两侧弯边的回弹,距离下陷区越远则影响越小.
卸载后的下陷区与两侧弯边总弯矩为
| $ \begin{array}{l} \Delta {M_{\rm{总}}} = \Delta {M_1} + \Delta {M_{2x}} + \Delta {M_3} = {\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;\;\;K{\left( {\frac{{1 + r}}{{\sqrt {1 + 2r} }}} \right)^{1 + n}}\frac{{\left( {L + 2b} \right){t^2}{{\left( {\frac{t}{{2\rho }}} \right)}^n}}}{{4\left( {1 + n} \right)}}. \end{array} $ | (13) |
其中b为下陷两端弯边长度,ΔM1、ΔM3为直弯边部分弯矩,下陷区及其两侧弯边的总惯性矩:
| $ {I_{\rm{总}}} = {I_1} + {I_j} + {I_3} = \frac{{\left[ {2b{L^2} + {{(\sqrt {{L^2} + {h^2}} )}^3}} \right]{t^3}}}{{12{L^2}}}. $ | (14) |
距离下陷区为b的弯边回弹为
| $ \begin{array}{l} \Delta \theta = \frac{{\Delta {M_{\rm{总}}}}}{{E'{I_{\rm{总}}}}} = \frac{{{L^3} + 2b{L^2}}}{{{{\left( {\sqrt {{L^2} + {h^2}} } \right)}^3} + 2b{L^2}}} \cdot \\ \;\;\;\;\;\;\;\;\;K{\left( {\frac{{1 + r}}{{\sqrt {1 + 2r} }}} \right)^{1 + n}}\frac{{3(1 - {\nu ^2}){{\left( {\frac{t}{{2\rho }}} \right)}^n}}}{{E\left( {1 + n} \right)t}}. \end{array} $ | (15) |
从而得出直弯边下陷区回弹补偿因子为
| $ f = \frac{{{L^3} + 2b{L^2}}}{{{{\left( {\sqrt {{L^2} + {h^2}} } \right)}^3} + 2b{L^2}}}. $ | (16) |
此时,回弹补偿公式为
| $ \Delta {\theta _{补偿}} = f \cdot \Delta \theta . $ | (17) |
其中f为补偿因子,Δθ为公式(7)计算的回弹角.
2 回弹补偿模块二次开发 2.1 数据库连接在飞机钣金制造过程中,“一步法”成形是国内采用的革新工艺,其核心是利用铝合金板料经淬火后,采用低温冷藏的办法,保持铝合金板料在新淬火状态下良好的塑性并一次完成成形工作.新淬火状态下板料性能可通过单向拉伸试验测定,将其开发成Access数据库,为回弹补偿计算提供材料参数.
访问Access数据库主要有以下4种方式:(1)ODBC (Open Database Connectivity)开放式数据库连接; (2) DAO (Data Access Object)数据访问对象集; (3) OLEDB (Object Link and Embedding Database)基于COM接口的技术; (4) ADO (ActiveX Data Object)是建立在OLEDB之上的高层数据库访问技术,是对OLEDB的封装.本文采用ADO方式对数据库进行提取和写入,窗口如图 4所示.

|
图 4 材料参数窗口 Figure 4 Material parameters window |
本文提出一种曲线法平面截取补偿算法对板料成形过程中回弹问题进行补偿,通过回弹函数分别计算圆角半径以及弯曲角度的回弹量,利用反向加或减的方式对其进行回弹补偿[12].本文采用CATIA二次开发来实现该算法,曲线法平面截取补偿理论是基于截取平面内的二维补偿方法,主要包括3部分操作:1)提取系统所需特征;2)弯曲圆角区域半径的回弹补偿;3)弯曲角度回弹补偿.
利用Visual C++将公式(16)基于CATIA二次开发出回弹补偿系统,针对长条U形钣金件进行回弹补偿,图 5为直弯边下陷零件工艺参数示意图,其中板将料厚度t=1 mm,圆角半径R=3 mm,弯边高度h=25 mm.

|
图 5 弯边工艺参数 Figure 5 Flanging process parameters |
通过CATIA二次开发的补偿系统对长条U形钣金件进行补偿,对于纯直弯边部分采用未修正的公式6进行补偿,补偿结果如图 6(a)所示.下陷区部分采用带有补偿因子的公式(16)进行补偿,补偿结果如图 6(b)所示.
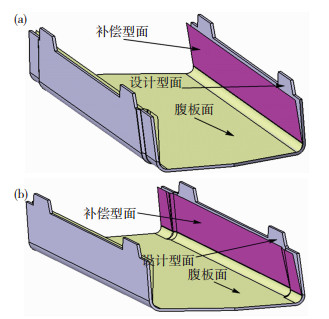
|
图 6 回弹补偿 Figure 6 Springback compensation |
为简化计算,提高效率,二次开发回弹补偿系统中将补偿完成的模具曲面导出,采用Pam-stamp 2G软件模拟来对回弹进行预测,建立有限元模型如图 7所示.主要由4部分组成:工作台、模具、板料和橡皮.模具和工作台为刚体,板料和橡皮为变形体,橡皮边界固定x、y平移自由度以及xyz方向的旋转,模具和工作台固定6个自由度,摩擦均为0.2[13],板料材料为2024铝合金,在压力的作用下橡皮下移变形使得板料与模具贴合,从而成形出合格的钣金零件.
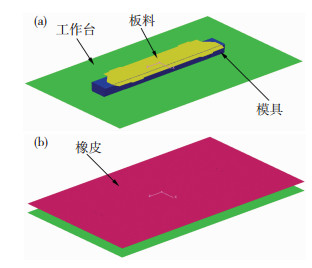
|
图 7 有限元分析模型 Figure 7 Finite element analysis model |
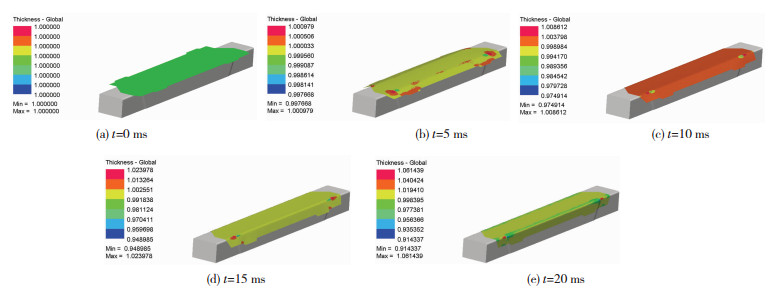
图 8所示为成形过程中板料厚度变化分布图,可以看出,下陷位置厚度明显增厚,不容易成形.图 9为板料回弹分布情况,从图中可以看出,经补偿后模具成形回弹很小且在公差范围内.
|
图 8 成形过程板料厚度分布图 Figure 8 Forming process blank thickness distribution:(a)T=0 ms; (b)T=5 ms; (c)T=10 ms; (d)T=15 ms; (e)T=20 ms |

|
图 9 回弹分布情况 Figure 9 Springback distribution |
试验过程中所用模具为采用二次开发补偿后模具,模具材料为Q235钢.试验选用ABB公司生产的QFC1.4 4-1000橡皮液压机,其工作效率高,省时高效,由于板料在成形过程中,使用不同润滑剂会出现不同的摩擦状况[14, 15],本试验选用SDL水基润滑剂并添加一定量的油酸钠.对板料进行橡皮成形试验,成形压力分别为40、50和60 MPa,试验后板料贴模情况如图 10所示.

|
图 10 板料贴模情况 Figure 10 Blank film situation |
成形出合格的直弯边下陷零件如图 11所示.从图 11(b)可以看出,当成形压力为60 MPa时,下陷效果较为明显.

|
图 11 实际成形零件照片 Figure 11 Photo of formed parts: (a)mass production; (b)the jogged zone photos |
试验结束后,采用通用量角器对图 11中所示直弯边带下陷弯边各位置的回弹角进行测量,结果见表 1.
| 表 1 各位置角度 Table 1 Each position angle |
从表 1可以得出,成形压力对回弹的影响较小,二次开发回弹补偿更精准且二次开发补偿误差均在0.5°之内.采用计算公式二次开发下陷区回弹补偿结果与试验值和模拟值比较如图 12所示.从图中可以看出越靠近下陷区,回弹越小,呈现出波动先增加后减小的趋势.

|
图 12 回弹补偿结果比较 Figure 12 Comparison of springback compensation results |
1) 根据刚度概念推导出基于补偿因子的下陷区回弹补偿公式.
2) 通过CATIA二次开发将补偿公式得以实现并与数据库进行连接,实现了材料参数的快速读取和写入.
3) 在数值模拟的基础上,成形出合格的下陷零件,验证了补偿公式的可靠性.
| [1] | SALA G. A numerical and experimental approach to optimise sheet stamping technologies:part 2-aluminium alloys rubber-forming[J]. Materials and Design,, 2001, 22(4): 299–315. DOI: 10.1016/S0261-3069(00)00088-1 |
| [2] | NADER ASNAFI. On stretch and shrink flanging of sheet aluminium by fluid forming[J]. Journal of Materials Processing Technology, 1999, 96(1-3): 198–214. DOI: 10.1016/S0924-0136(99)00352-0 |
| [3] | LIVATYALI H, ALTAN T. Prediction and elimination of springback in straight flanging using computer aided design methods. Part 1: Experimental investigations[J]. J Mater Process Technol, 2001, 117(1-2): 262–268. DOI: 10.1016/S0924-0136(01)01164-5 |
| [4] | NANU N, BRABIE G. Analytical model for prediction of springback parameters in the case of U stretch-bending process as a function of stresses distribution in the sheet thickness[J]. International Journal of Mechanical Sciences, 2012, 64(1): 11–21. DOI: 10.1016/j.ijmecsci.2012.08.007 |
| [5] | WAGONER R H, WANG J F, LI M. Springback[J]. The Ohio State University, 2006, 14(B): 733–755. |
| [6] | SUN Zhiying, LANG Lihui. Effect of stress distribution on springback in hydroforming process[J]. International Journal of Advanced Manufacturing Technology, 2017, 93(5-8): 1–10. |
| [7] |
裴兴林, 刘书岩. 基于试验设计法的L形薄板弯曲回弹预测[J]. 机械制造, 2010, 48(7): 73–76.
PEI Xinglin, LIU Shuyan. Prediction of bending rebound of L-shaped thin plate based on experimental design method[J]. Machinery, 2010, 48(7): 73–76. DOI: 10.3969/j.issn.1000-4998.2010.07.027 |
| [8] |
阳湘安, 阮锋, 周驰. 基于回弹控制的板料成形工艺多目标优化[J]. 华南理工大学学报(自然科学版), 2010, 38(12): 7–13.
YANG Xiangan, RUAN Feng, ZHOU Chi. Multi-objective optimization of forming process of sheet metal based on springback control[J]. Journal of South China University of Technology(Natural Science Edition), 2010, 38(12): 7–13. DOI: 10.3969/j.issn.1000-565X.2010.12.002 |
| [9] |
陈磊, 李善良, 张亚兵. 板料凹弯边橡皮成形回弹分析与控制方法[J]. 塑性工程学报, 2010, 17(2): 1–5.
CHEN Lei, LI Shanliang, ZHANG Yabing. Analysis and control methods on springback of stretch flanging during rubber fluid forming[J]. Journal of Plasticity Engineering, 2010, 17(2): 1–5. DOI: 10.3969/j.issn.1007-2012.2010.02.001 |
| [10] | LEU D K. A simplified approach for evaluating bendability and springback in plastic bending of anisotropic sheet metals[J]. Journal of Materials Processing Technology, 1997, 66(1-3): 9–17. DOI: 10.1016/S0924-0136(96)02453-3 |
| [11] |
李贵, 崔赛赛, 陈志平, 等. 先进高强钢DP1000地板中央通道的成形回弹及补偿研究[J]. 材料科学与工艺, 2018, 26(1): 39–46.
LI Gui, CUI Saisai, CHEN Zhiping, et al. Research on the forming springback and compensation of floor panel tunnel of advanced high strength steel DP1000[J]. Materials Science and Technology, 2018, 26(1): 39–46. DOI: 10.11951/j.issn.1005-0299.20170221 |
| [12] |
刘闯, 李锦鹏, 王俊彪. 一种带下陷框肋零件弯边变系数回弹精确补偿方法, CN 106295060 A[P]. 2017. LIU Chuang, LI Jinpeng, WANG Junbiao. One kind with sagging box ribbed flange parts with variable coefficients rebound Accurate Compensation Method:, CN 106295060 A[P]. 2017. |
| [13] |
张凌云, 周帅, 孟伟琪, 等. 基于响应面法橡皮成形侧压块参数优化及验证[J]. 材料科学与工艺, 2018, 26(2): 15–70.
ZHANG Lingyun, ZHOU Shuai, MENG Weiqi, et al. Parameters optimization of rubber forming side blank holder based on response surface methodology and verified[J]. Materials Science and Technology, 2018, 26(2): 15–70. DOI: 10.11951/j.issn.1005-0299.20170060 |
| [14] | SUN Z, LANG L. Study on hydroforming process and springback control of large sheet with weak rigidity[J]. International Journal of Precision Engineering & Manufacturing, 2017, 18(6): 903–912. |
| [15] | SINKE J. Spring back of curved flanges of rubber formed aluminum parts[J]. Key Engineering Materials, 2013, 554-557: 1851–1855. DOI: 10.4028/www.scientific.net/KEM.554-557 |
 2018, Vol. 26
2018, Vol. 26


