近些年来,我国稀土电解行业发展迅猛.2016年,我国稀土总产量达到20万吨以上,可以满足全世界的需要[1].但是,我国稀土电解槽早期损坏严重,平均槽寿命只有八十多天,难以达到设计寿命,一直是我国稀土电解行业未能解决的关键问题之一.在大量稀土电解槽早期损坏事故中,石墨内衬开裂,断裂和穿孔等这样的情况很多.因此,作为电解槽中最薄弱的环节,石墨内衬越来越被稀土电解界所关注[2-4].刘建刚[5]改进了筑炉工艺以及使用了新型筑炉材料,从而使电解炉寿命提高到原来的三倍.陈德宏等[6]将Si3N4结合SiC材料代替石墨作为电解槽的内衬进行实验,结果表明,该内衬在电解过程中腐蚀严重,主要受腐蚀的是含Si3N4的结合相.任永红等[7]介绍了一种以NdOF为主要成分的内衬材料取代石墨内衬,通过实践表明,将该内衬应用在稀土电解槽可以提高其性能,使其工作寿命增加.
以上研究表明稀土电解时空气和电解质会向石墨内衬内部渗透,进而氧化腐蚀内衬,从而导致石墨内衬加快破损,而这与石墨内衬的孔隙构造有关[8-10].大量研究已经证明显微CT技术在研究多孔材料孔隙结构方面有定量化、快速化、分辨率高等优点[11-15].郁邦永等[16]利用CT扫描研究了饱和破碎灰岩的孔隙结构.张巍等[17]利用显微CT系统对南京粉砂的孔隙结构进行了定量表征.然而,目前基于显微CT技术对石墨内衬孔隙结构表征的研究报道很少.
本文利用显微CT对石墨内衬进行了扫描分析.以显微CT扫描获取的数字岩心为基础建立图形学模型,度量孔喉的几何参数,并利用分形维数表征了石墨内衬孔隙结构的分形特征和孔隙率,以期构建一种评价石墨内衬质量的新方法,从而为稀土电解槽内衬的优化设计提供一定的技术参数和理论依据.
1 实验 1.1 实验设备显微CT分析系统为天津三英精密仪器股份有限公司生产的nano-Voxel 2000 X射线三维显微镜,其最高分辨率可以达到0.5 μm,采用了基于透镜耦合的光耦探测器,有非常高的灰度动态范围和很好的图像质量.
1.2 测试方法实验样品取自稀土电解槽石墨内衬,扫描前,将石墨内衬制成近似圆柱状待测样品,采用1 μm的体素分辨率对样品扫描成像,各项扫描参数见表 1.用专用工具将待测石墨内衬样品固定在显微CT扫描旋转工作台的中心位置,并且让样品与旋转工作台保持垂直,这样可以保证试件有足够高的放大倍数,如图 1所示.
| 表 1 显微CT扫描参数 Table 1 Microscopic CT scanning parameters |

|
图 1 石墨内衬显微CT扫描实验 Figure 1 Micro CT scanning experiment of graphite lining |
将扫描后的图片进行二维重建得到一系列原始CT灰度图像,共825幅CT灰度图像.选取其中一副CT灰度图像,如图 2(a)所示.由于CT图像围绕外围区域与扫描样品无关,为了方便后续的CT图像预处理,选取原始CT图像上521像素×521像素的一个正方形区域图 2(b)作为该石墨内衬样品孔隙结构的研究对象.然后对选取的图像进行二值化处理得到图 2(c),图像中黑色表示样品的孔隙,白色表示样品中的固体物质.

|
图 2 原始CT图像预处理过程 Figure 2 Original CT image preprocessing process (a) Original CT grayscale images of graphite-based samples; (b)Selected image; (c)Binarized image |
在CT图像预处理的基础上,对序列灰度CT图像进行三维重建,三维重建就是将显微CT扫描得到的一系列CT平面灰度图像(图 3(a))按照一定的顺序依次叠放在一起,这样就可以用平面灰度图像构建出三维数字CT图像(图 3(b)).然后通过阈值划分提取出样品CT三维图像中的孔隙,并用球棒模型进行示意,得到样品孔隙的三维模型,如图 3(c)所示.从样品孔隙三维模型可以看出该样品内部孔隙数量多,而且结构复杂,各孔隙之间连通较好.在进行稀土电解时,空气与电解质在石墨内衬中的流动路径多,导致其与石墨内衬的接触面积大,石墨内衬的腐蚀会变快,进而缩短了稀土电解槽槽体寿命.

|
图 3 样品三维CT图像处理 Figure 3 3D CT image processing of the sample: (a) sample sequence CT grayscale of the sample; (b) 3D CT image of the sample; (c) 3D pore model of the sample |
利用CT图像分析软件对石墨内衬样品的序列CT图像进行处理后,统计孔隙总像素数P0和固体总像素数Pa.则该石墨内衬的孔隙度P可以表示为:
| $ P = \frac{{{P_0}}}{{{P_0} + {P_{\rm{a}}}}}. $ | (1) |
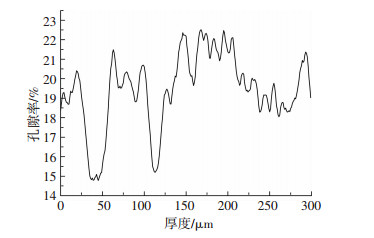
根据式(1),显微CT扫描得到的孔隙率分布,如图 4所示.
|
图 4 孔隙度分布图 Figure 4 Porosity distribution |
由图 4可以看出,该样品的孔隙分布不均匀,大都在18%~23%.实验中,测得石墨内衬样品的平均孔隙度为19.44%,这表明该石墨内衬内部拥有较多孔隙.在进行稀土金属电解过程中,这些孔隙会为电解质和空气提供场所,为它们的流动提供路径,进而增大了电解质和空气与石墨内衬的接触面积,从而加速了石墨内衬的腐蚀,缩短了稀土电解槽槽体寿命.
2.1.2 孔喉尺寸分析利用CT扫描分析系统对石墨内衬样品内部孔喉进行定量分析.结果如表 2所示.
| 表 2 孔喉尺寸定量分析数据 Table 2 Quantitative analysis data of pore throat size |
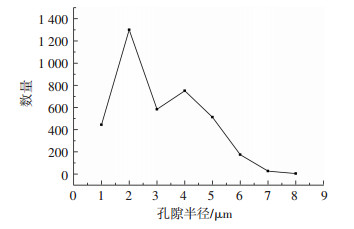
选取尺寸为1~7.79 μm的孔隙进行数量统计,如图 5所示.结果表明,该石墨内衬孔隙的尺寸分布主要集中在1~6 μm,其中孔隙半径为2 μm左右的的孔隙数量最多.选取尺寸为1~5.65 μm的喉道进行数量统计,如图 6所示.结果表明,该石墨内衬喉道的尺寸主要集中在1~5 μm,其中喉道半径为1 μm左右的喉道数量比较多.
|
图 5 孔隙半径分布图 Figure 5 Pore radius distribution |

|
图 6 喉道半径分布图 Figure 6 Throat radius distribution |
从以上分析结果可以看出,该石墨内衬样品中孔喉数量多,而且孔隙与喉道的尺寸相差不大,从而导致其孔隙结构的平均孔喉比值较小,仅仅为2.28.孔喉比值较小意味着孔隙间有较大的喉道连通,在进行稀土电解时,空气和电解质在石墨内衬内部的流动阻力较小,使空气和电解质在石墨内衬内部流动速度加快,这样就增加了空气和电解质与石墨内衬的接触面积,从而加速了石墨内衬的腐蚀,导致电解槽槽体寿命大大缩短.
2.1.3 孔喉形状因子分析孔喉形状因子是定量表征孔喉形状不规则程度的参数.形状因子G定义为[18]
| $G = A/{P^{2}}. $ | (2) |
式中:A为孔喉的截面面积,P为周长.根据上式可以算出圆形孔喉的形状因子为G=πr2/4π2r2=0.079 6,同理可以得出正方形孔喉的形状因子为0.062 5,三角形孔喉和长宽比大于2.8的矩形,呈缝状结构的孔喉形状因子为0~0.048 1.
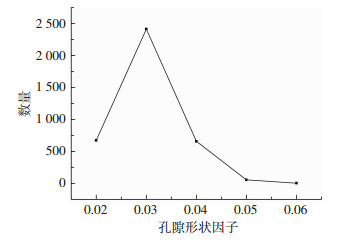
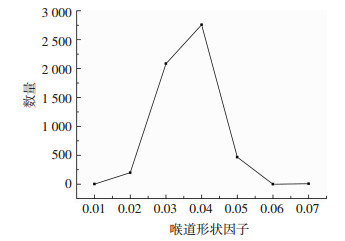
图 7是石墨内衬孔隙的形状因子分布图.从图中可以看到,该石墨内衬孔隙的形状因子主要分布在0.02~0.04,孔隙形状以三角形为主;图 8是石墨内衬喉道形状因子分布图.由图可知,该样品喉道形状因子参数主要分布在0.02~0.05,喉道形状以三角形为主,部分喉道形状为四边形.
|
图 7 孔隙形状因子分布图 Figure 7 Pore shape factor distribution |
|
图 8 喉道形状因子分布图 Figure 8 Throat shape factor distribution |
基于上述分析可以得出,该石墨内衬的孔喉形状大多不规则,呈三角形状的最多,其中有少量的喉道呈四边形.从孔喉的几何形状这一方面来讲,在进行稀土电解的时候,由于孔喉形状不规则,相对于圆形孔喉来讲,不规则的孔喉存在边角结构,导致空气和电解质在石墨内衬中的流动阻力增大,使其在石墨内衬中流动速度减慢,从而减小了空气和电解质与石墨内衬的接触面积,减缓了石墨内衬的破损,提高了电解槽槽体寿命.
2.2 石墨内衬孔隙结构的分形分析 2.2.1 孔隙结构的分形特征分形维数是分形几何的特征参数,可以有效的表征石墨内衬孔隙分布情况.研究对象不同,计算它们的分形维数的方法也有差别.其中盒维数法计算简便,物理意义也比较直观,在多孔介质孔隙结构研究方面应用广泛.盒维数的定义为
| $ D = \mathop {{\rm{lim}}}\limits_{\delta \to 0} \frac{{{\rm{lg}}{N_\delta }\left( F \right)}}{{ - {\rm{lg}}\delta }}. $ | (3) |
式中:Nδ(F)是覆盖Rn空间中子集F、尺寸δ的单元最小数目.
石墨内衬二值化CT切片的分形维数可以利用像素覆盖法来计算.将一副M×M像素的二值化CT图像划分为边长为δi的网格,其中黑色像素表示孔隙,统计覆盖图像上黑色像素的网格数量Nδi, 当δi→0时,lgNδi/(-lgδi)→D, 因此可以得到一系列数据对(δi, Nδi),然后绘制(δi, Nδi)双对数坐标图,拟合得到直线方程如下:
| $ {\rm{lg}}{N_\delta } = D \cdot ( - {\rm{lg}}\delta ) + {\rm{lg}}N. $ | (4) |
式中:斜率D是孔隙结构的分形维数,N为孔隙数量的分布初值.
本文采用盒维数法来计算石墨内衬孔隙构造的分形维数.图 9给出了石墨内衬第285层与718层CT切片孔隙的分形数据,其中直线的斜率为孔隙的分形维数D,从结果来看,相关系数R2基本都在0.9以上,因此,用盒维数法得到的石墨样品孔隙的分形维数是有效的,同时也表明该石墨内衬孔隙结构有很好的分形规律.

|
图 9 二值化CT切片的分形维数 Figure 9 Fractal dimension of binarized CT slices: (a)XY285 slice; (b)XY718 slice |
由以上结果可以得到,该石墨内衬第285层CT切片的孔隙分形维数为1.667 6,第718层CT切片的孔隙分形维数为1.652 9.XY285的分形维数比XY718的分形维数大说明XY285切片中孔隙分布比较复杂,大孔隙占据主要位置.而XY718相对于XY285来说,其CT切片中的孔隙分布比较均匀,小孔隙的数量比较多.这从石墨内衬的二值化切片图像上(图 10)也可以看出,XY285中主要孔隙形态不规则,大孔隙比较多,因此其分形维数较大;反观XY718二值化切片,可以看到切片中小孔隙很多,孔隙结构简单,其分形维数比XY285小.这也证实了孔隙分形维数可以定量表征石墨内衬孔隙分布的复杂程度.

|
图 10 CT灰度切片及其二值化图 Figure 10 XY gray slices of XY285 and XY718 and their binarization graphs:(a)XY285 slice; (b)XY718 slice |
孔隙率是衡量石墨内衬性能的一个重要参数,因此,孔隙率的大小对石墨内衬的性能来说是很重要的.此外,石墨内衬中孔隙结构复杂,符合分形多孔介质特征.
由分形理论知,存在于d维欧氏空间中的一个分形体的物理量应该有如下关系[19]:
| $ M\left( L \right) \propto {L^{\rm{D}}}. $ | (5) |
式中:M(L)为待测物理量;L为物体的线度;D为该分形体的分形维数且有d-1≤D≤d.
现将石墨内衬看作是固相分形体,那么与之共存的是石墨内衬中的孔隙,其孔隙半径的大小r和累积的孔隙数量N(r)存在以下关系:
| $ N\left( r \right) = \int_r^{{r_{{\rm{max}}}}} {P\left( r \right){\rm{d}}r = A{r^{ - D}}.} $ | (6) |
式中:rmax为石墨样品中的最大孔隙半径;A为比例系数;D为石墨内衬的分形维数;P(r)为石墨孔隙半径的分布密度函数.
由式(6)可以得到在一定的孔隙尺寸分布下,单位石墨样品中的总孔隙数量为
| $ N = Ar_{{\rm{min}}}^{ - D} - Ar_{{\rm{max}}}^{ - D} = A(r_{{\rm{min}}}^{ - D} - r_{{\rm{max}}}^{ - D}). $ | (7) |
式中:N为单位石墨样品中的孔隙数;rmax为石墨的最大孔隙半径;rmin为石墨的最小孔隙半径;A为比例系数.
将式(6)两边对r求导,得P(r)的表达式为
| $ P\left( r \right) = - \frac{{{\rm{d}}N\left( r \right)}}{{{\rm{d}}r}} = AD{r^{ - (1 + D)}}. $ | (8) |
由P(r)可得石墨的孔隙率与其分形维数的关系式如下[20]:
| $ \varphi = \int_{{r_{{\rm{min}}}}}^{{r_{{\rm{max}}}}} {P\left( r \right){r^3}{\rm{d}}r = \frac{{AD}}{{3 - D}}(r_{{\rm{max}}}^{3 - D} - r_{{\rm{min}}}^{3 - D}).} $ | (9) |
综合式(7)和(9)可得
| $ \varphi = \frac{{ND}}{{3 - D}}(\frac{{r_{{\rm{max}}}^{3 - D} - r_{{\rm{min}}}^{3 - D}}}{{r_{{\rm{min}}}^{ - D} - r_{{\rm{max}}}^{ - D}}}). $ | (10) |
由式(10)可以看出,石墨内衬的孔隙度取决于分形维数D,孔隙尺寸的上下限rmax, rmin,以及单位石墨内衬的孔隙数N.如果知道上述参数,我们就可以算出石墨内衬的孔隙率,相反,可以由实验测得石墨内衬的孔隙率来计算其分形维数.
对所选石墨内衬样品CT图像进行分析计算,统计单位体积石墨内衬的孔隙数量N,孔隙尺寸的上下限以及计算其分形维数.将上述数据代入式(10)计算得到石墨内衬的孔隙率,如表 3所示.
| 表 3 石墨内衬孔隙率计算结果 Table 3 Calculation results of porosity in graphite lining |
由表 3可以看出,该石墨内衬的理论孔隙率为21.46%,与实际孔隙率19.44%相差不大.由此可以得出,通过理论公式计算的石墨内衬的孔隙率有较好的准确性,可以运用这种方法来预测石墨内衬的实际孔隙率.同样,如果已经知道石墨内衬的孔隙率,可求得其孔隙结构的分形维数,这也为探究石墨内衬孔隙结构的分形特征提供了一个新的办法.
4 结论1) 基于显微CT扫描,能对石墨内衬的孔喉结构进行定量表征.实验测得该样品的孔隙度为19.44%,孔喉半径大都在1~6 μm,孔喉形状因子为0.02~0.05,平均孔喉比、平均孔隙体积、平均喉道体积分别为2.28、1177.64、106.19 μm3.这些孔喉参数可以用来分析空气和电解质在石墨内衬中的流动情况,进而分析石墨内衬的氧化腐蚀程度.
2) 分形维数D可以精确的描述石墨内衬孔隙结构的不规则程度.分形维数的变化与孔隙结构特征有着密切的关系.随着石墨内衬孔隙结构复杂程度的增加,其相应的分形维数就变大.
3) 由石墨内衬孔隙率的分形关系式计算的理论孔隙率为21.46%,与其实际孔隙率19.44%相差很小,有很好的准确性,可以运用这种方法来预测石墨内衬的孔隙率,从而构建了一个探究石墨内衬孔隙结构分形特征的新办法, 同时也为稀土电解槽内衬的优化设计提供一定的技术参数和理论依据.
| [1] |
周明, 刘祥林. 中国稀土生产、贸易与储备分析[J]. 对外经贸, 2017, 03(3): 57–60.
ZHOU Ming, LIU Xianglin. Analysis of China's rare earth production, trade and reserve[J]. Foreign Trade, 2017, 03(3): 57–60. |
| [2] | LUO X W, ROBIN J C, YU S Y. Effect of temperature on graphite oxidation behavior[J]. Nuclear Engineering and Design, 2004, 227(3): 273–280. DOI: 10.1016/j.nucengdes.2003.11.004 |
| [3] |
石富. 稀土电解槽的研究现状及发展趋势[J]. 中国稀土学报, 2007, 25(S1): 70–76.
SHI Fu. Research status and development trend of rare earth electrolyzer[J]. Chinese Journal of Rare Earths, 2007, 25(S1): 70–76. |
| [4] |
杨斌清, 邓宇民, 杨安. 提高稀土金属电解炉使用寿命的研究及生产实践[J]. 江西冶金, 2001, 21(3, 4): 63–65.
YANG Binqing, DENG Yumin, YANG An. Research and production practice of improving service life of rare earth metal electrolytic furnace[J]. Jiangxi Metallurgy, 2001, 21(3, 4): 63–65. |
| [5] |
刘建刚. 稀土熔盐电解炉筑炉工艺改进[J]. 广东化工, 2015, 42(6): 52–59.
LIU Jiangang. Improvement of building technology for rare earth molten salt electrolytic furnace[J]. Guangdong Chemical Industry, 2015, 42(6): 52–59. |
| [6] |
陈德宏, 颜世宏, 李宗安, 等. Si3N4结合SiC材料在稀土电解槽中的应用及效果[J]. 稀土, 2012, 37(3): 12–15.
CHEN Dehong, YAN Shihong, LI Zongan, et al. Application and effect of Si3N4 combined with SiC material in rare earth electrolytic cell[J]. Rare Earth, 2012, 37(3): 12–15. DOI: 10.3969/j.issn.1004-0277.2012.03.003 |
| [7] |
任永红, 陈国华, 张志军, 等. 氟氧化钕耐火材料的研制与应用[J]. 耐火材料, 2003, 03: 147–149.
REN Yonghong, CHEN Guohua, ZHANG Zhijun, et al. Preparation and application of neodymium oxide refractory[J]. Refractory Material, 2003, 03: 147–149. DOI: 10.3969/j.issn.1001-1935.2003.03.008 |
| [8] |
李想, 薛济来, 郎光辉, 等. 铝用石墨质阴极不同焙烧温度下孔隙结构演化[J]. 北京科技大学学报, 2014, 36(9): 1233–1240.
LI Xiang, XUE Jilai, LANG Guanghui, et al. Pore structure evolution of graphite cathode for aluminum under different calcination temperatures[J]. Journal of University of Science and Technology Beijing, 2014, 36(9): 1233–1240. |
| [9] |
刑鹏飞. 稀土熔盐电解石墨阳极的腐蚀与防护[J]. 稀土, 1996, 17(2): 49–51.
XING Pengfei. Corrosion and protection of graphite anode in rare earth molten salt electrolysis[J]. Rare Earth, 1996, 17(2): 49–51. |
| [10] |
刘中兴, 徐子娟, 王伟, 等. 稀土电解槽石墨阳极的研究[J]. 有色金属(冶炼部分), 2014, 01(1): 45–49.
LIU Zhongxing, XU Zijuan, WANG Wei, et al. Study on graphite anode of rare earth electrolytic cell[J]. Nonferrous Metals (smelting parts), 2014, 01(1): 45–49. DOI: 10.3969/j.issn.1007-7545.2014.01.012 |
| [11] | KAREN M.STEEL, ROBIN E., DAWSON DAVID R, et al. Use of rheometry and micro-CT analysis to understand pore structure development[J]. Fuel Processing Technology, 2017, 155: 106–113. DOI: 10.1016/j.fuproc.2016.04.027 |
| [12] | SUN Wei, HOU Kepeng, YANG Zhiquan, et al. X-ray CT three-dimensional reconstruction and discrete element analysis of the cement paste backfill pore structure under uniaxial compression[J]. Construction and Building Materials, 2017, 138: 69–78. DOI: 10.1016/j.conbuildmat.2017.01.088 |
| [13] | AI Li, ZHAO Jiafei, WNAG Jiaqi, et al. Analyzing permeability of the irregular porous media containing methane hydrate using pore network model combined with CT[J]. Energy Procedia, 2017, 105: 4802–4807. DOI: 10.1016/j.egypro.2017.03.950 |
| [14] | Akira Sato, Yuzo Obara. Analysis of pore structure and water permeation property of a shale rock by means of X-ray CT[J]. Procedia Engineering, 2017, 191: 666–673. DOI: 10.1016/j.proeng.2017.05.230 |
| [15] | JONATHAN P. MATHEWS, QUENTIN P. Campbell, XU Hao, et al. A review of the application of X-ray computed tomography to the study of coal[J]. Fuel, 2017, 209: 10–24. DOI: 10.1016/j.fuel.2017.07.079 |
| [16] |
郁邦永, 陈占清, 冯梅梅, 等. 基于CT扫描的饱和破碎灰岩侧限压缩下微观结构演化特征[J]. 煤炭学报, 2017, 42(2): 367–372.
YU Bangyong, CHEN Zhanqing, FENG Meimei, et al. Microstructural evolution characteristics of saturated crushed limestone under lateral compression based on CT scanning[J]. Journal of Coal Industry, 2017, 42(2): 367–372. |
| [17] |
张巍, 梁小龙, 唐心煜, 等. 显微CT扫描南京粉砂空间孔隙结构的精细化表征[J]. 岩土工程学报, 2017, 39(4): 683–689.
ZHANG Wei, LIANG Xiaolong, TANG Xinyu, et al. Fine microscopic characterization of spatial pore structure of silty sand in Nanjing by micro CT scanning[J]. Journal of Geotechnical Engineering, 2017, 39(4): 683–689. |
| [18] |
张天付, 谢淑云, 王鑫, 等. 孔隙型储层的孔隙系统三维量化表征——以四川、塔里木盆地白云岩为例[J]. 海相油气地质, 2016, 21(4): 1–10.
ZHANG Tianfu, XIE Shuyun, WANG Xin, et al. Three dimensional quantitative characterization of pore system in porous reservoirs -- a case study of dolomite in Sichuan and Tarim Basin[J]. Marine Origin Petroleum Geology, 2016, 21(4): 1–10. DOI: 10.3969/j.issn.1672-9854.2016.04.001 |
| [19] |
樊贵超, 钟登华, 任炳昱, 等. 基于分形理论的坝基裂隙岩体注灰量与导水率关系研究[J]. 水利学报, 2017, 48(5): 576–587.
FAN Guichao, ZHONG Denghua, REN Bingyu, et al. Study on relationship between ash injection volume and hydraulic conductivity of fractured rock mass of dam foundation based on Fractal Theory[J]. Journal of HyDraulic Engineering, 2017, 48(5): 576–587. |
| [20] |
吴国铭, 李熙喆, 高树生, 等. 基于CT图像分析探究孔洞型碳酸盐岩储层分维值与微观结构参数关系[J]. 科学技术与工程, 2016, 16(8): 87–92.
WU Guoming, LI Xizhe, GAO Shusheng, et al. Based on CT image analysis, the relationship between fractal dimension and microstructure parameter of pore type carbonate reservoir is studied[J]. Science & Technology and Engineering, 2016, 16(8): 87–92. DOI: 10.3969/j.issn.1671-1815.2016.08.013 |
 2018, Vol. 26
2018, Vol. 26


