2. 装备再制造技术国防科技重点实验室(装甲兵工程学院),北京 100072
2. National Key Lab for Remanufacturing (Academy of Armored Forces Engineering), Beijing 100072, China
再制造是废旧产品高技术修复、改造的产业化[1].随着现代制造业对节约资源、保护环境要求的不断提高,再制造技术正在成为绿色制造业的新方向.再制造过程中,为了提高零件的表面性能和进行尺寸修复,热喷涂技术得到了广泛应用[2].
为保证服役安全,目前重要机械装备主承力构件仍然沿用传统的无限寿命或安全寿命设计方法.这种设计思路源于人们对主承载结构件复杂的失效机制及劣化规律难以详尽掌握,不得不在设计阶段为零件留下较高的安全裕量[3].原型产品预留的超长寿命储备使得退役后的废旧件仍有足够的强度冗余,再制造毛坯基体结构具有充足的承载能力,这是再制造产品能够二次服役的力学基础.但是,再制造毛坯是具有既往服役历史的废旧零件,在工况条件作用下,基体结构可能产生某种程度的劣化和微损伤累积,以致存在隐性或显性缺陷.显性缺陷具有宏观尺寸,易于在再制造毛坯的检测评价环节发现并处理;隐性损伤尤其是早期微损伤,因不具有可分辨的物理参量变化而难以甄别[4].在二次服役时,再制造毛坯作为再制造零件承载的基础结构,再次受到工况载荷,特别是交变载荷的激励,其隐性损伤更容易萌生演化,发展为显性裂纹[5].
裂纹严重危害着热喷涂再制造零件结构的完整性,从而影响构件的性能[6].过低的评估其对热喷涂再制造件结构完整性的影响,可能危害再制造产品的使用安全,降低其服役寿命;而如果过高的评估裂纹缺陷的危害作用,将致使产品进行不必要的修复甚至提前报废,从而造成经济损失[7-9].目前对再制造毛坯的缺陷缺少一个明确的界限,例如对裂纹埋藏深度安全范围的界定、裂纹尺寸的界定等,即缺陷的位置、大小和性质达到何种情况就不能用来进行再制造.因此,为了保障再制造产品的质量,对再制造毛坯中的裂纹进行研究显得至关重要.已有大量学者对裂纹检测方法进行研究,如电磁检测技术对再制造涂覆层与基体材料具有选择性,再制造涂覆层的非均匀结构急剧降低其检测精度,难以发现涂覆层皮下缺陷[10];超声波检测时受喷涂层多孔疏松结构影响,衰减严重,同时涂层与基体异质界面又对入射的高频超声波产生界面反射和散射,对再制造毛坯基体隐性损伤演化成的疲劳裂纹难以发现[11];而声发射检测技术一方面必须施加外部载荷,在加载状态下才能采集包含大量动态噪声的裂纹信号;另一方面受涂覆层的遮挡,基体裂纹信号微弱,难以辨识基体与涂层开裂信号,定量评估非常困难[12];射线检测时对入射射线角度与裂纹位向有严格要求,不适用于基体结构复杂、涂层疏松多孔的再制造零件[13];机器视觉等光学检测技术受再制造涂覆层的隔断亦难以发现表皮下异常缺陷结构.裂纹扩展是一个动态过程,利用实验法观察裂纹具有一定的难度,并且再制造产品由于涂层与基体的性能存在差异,裂纹扩展情况更为复杂[14-16],因此本文使用大型有限元分析软件ABAQUS,利用扩展有限元和内聚力单元结合的方法,对再制造件基体内部裂纹的扩展行为进行深入研究,并探寻基体裂纹倾斜角度、裂纹埋藏深度及位置对热喷涂再制造件基体裂纹扩展行为的影响规律.
1 实验 1.1 扩展有限元扩展有限元(XFEM)在断裂问题的分析中,相较于传统有限元法将裂纹尖端应力的奇异性现象考虑在内.传统有限元只在有限元建模过程中对裂纹尖端位置进行网格细分,确定试样边界条件后即进行有限元计算求解.通过数值分析计算得到每个单元的位移场、应变场和应力场,再利用位移场渐近的关系,由裂纹尖端附近一个节点的位移来推导出裂尖的位移.因而利用传统有限元法分析断裂问题,为了得到比较合理、准确的计算结果,必须对模型进行精细的网格划分,这样无疑大大增加了计算时间.扩展有限元允许裂纹在单元内部扩展和穿过单元,因而可以在规则网格上计算复杂形状的裂纹,同时缩短了计算时间[17].
1.2 有限元模型为了研究再制造零件基体裂纹的扩展行为,使用有限元软件ABAQUS对三点弯曲试验下的裂纹扩展行为进行数值模拟研究.试样分为2种形式,一种为基体中心带有垂直裂纹的三点弯曲试样,另一种为基体中心带有45°倾斜裂纹的三点弯曲试样.两种试样基体的长度均为180 mm、宽度为10 mm、厚度为10 mm,涂层厚1.5 mm,其中垂直裂纹长1 mm,45°倾斜裂纹长
| 表 1 材料力学参数 Table 1 Material mechanical parameters |
实验所采用的基体材料为45钢,使用线切割技术在基体的中心位置分别预制与模拟相同的初始裂纹,其中垂直裂纹长1 mm,45°倾斜裂纹长
| 表 2 3Cr13涂层成分 Table 2 Ingredients of 3Cr13coating |
| 表 3 3Cr13喷涂参数 Table 3 Spraying parameters of 3Cr13 |
通过有限元模拟得到的两种试样在三点弯曲试验下基体裂纹扩展的轮廓图如图 1所示.从图 1可以看出,随着载荷的增加,带有垂直裂纹的试样沿着基体厚度方向竖直扩展.而带有45°倾斜裂纹的试样在竖直方向开始起裂,随后向基体扩展,其扩展路径向试样中心线处靠近,同时部分基体裂纹在涂层-基体界面发生偏转并沿着涂层-基体界面扩展.
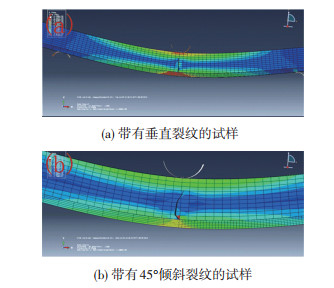
|
图 1 三点弯曲试验下裂纹扩展的轮廓图 Figure 1 Outline drawing of crack propagation under the three-point bending test:(a)specimen with vertical crack; (b)specimen with 45°inclined crack |
为了进一步深入研究基体裂纹埋藏深度对其扩展行为的影响,在基体内部分别设置了距涂覆层-基体界面0、1、2、3、4、5 mm的基体埋藏裂纹,并对其扩展行为进行了数值模拟.其中设置的垂直裂纹初始长度为1 mm,倾斜裂纹的初始长度为
| 表 4 不同埋藏深度下试样发生裂纹扩展时的临界载荷 Table 4 Critical coad for crack propagation at diffevent burial depth |
表 4中的结果表明,临界开裂载荷随着裂纹埋藏深度的增加而增加,在模拟的过程中甚至发现,当埋藏深度达到一定程度时,没有出现裂纹扩展现象.为了验证模拟结果的可靠性,对该现象进行理论分析.
在三点弯曲过程中,试样下部分受拉伸,上部分受挤压,在其断面上存在一个既不受拉,又不受压的中性层,对于单一材料的试样,其中性层位于几何中心,而对于涂层-基体体系,由于涂层和基体的物理性能存在差异,其中性层的位置往往不在其几何中心.此时,中性层的位置可根据下式确定:
| $ \xi = \frac{{{E_{\rm{s}}}h_{\rm{s}}^2 - {E_{\rm{c}}}h_{\rm{c}}^2}}{{2\left( {{E_{\rm{s}}}{h_{\rm{s}}} + {E_{\rm{c}}}{h_{\rm{c}}}} \right)}}. $ | (1) |
式中:hC、hS分别为涂层和基体的厚度; ξ为界面到中性层的距离.在本研究中hC=1.5 mm,hS=10 mm,ES=210 GPa,EC=230 GPa,经过计算可以得到ξ=4.189 mm.即本研究中的试样,其中性层距涂层-基体界面4.189 mm.
图 2为不同材料组成的复合梁在三点弯曲试验过程中的应力分布图,从图 2中可以看出试样下部分的拉伸应力随Y轴方向的增加而增加.因而当基体裂纹距界面距离增大时,拉应力随之下降,因而裂纹发生扩展时压头所需要施加的临界载荷越大.当埋藏裂纹深度超过4.189 mm时,即基体裂纹出现在中性层上方时,该裂纹尖端在三点弯曲过程中受挤压,因而没有出现裂纹扩展现象,此时的基体裂纹即可认为是安全的.以上分析表明,模拟结果与理论推导相符,验证了模拟结果的可靠性.
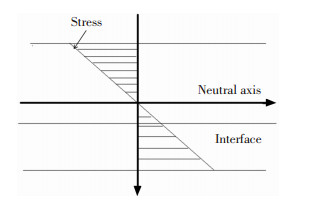
|
图 2 三点弯曲试验中横截面的应力分布 Figure 2 Stress distribution of cross section in three-point bending test |
在基体内部设置了如图 3所示的偏置裂纹,偏置裂纹距离试样的中心线10 mm.其中(a)和(c)中的初始裂纹长1 mm,(b)中的初始裂纹长

|
图 3 基体内部含偏置裂纹的试样模型
Figure 3 Specimen model with offset crack inside the substrate(a) 1mm; (b) |
通过有限元分析,得到三点弯曲试验下基体内部偏置裂纹的扩展形貌如图 4所示.从图中可以看到,3(a)中的垂直裂纹沿着基体厚度方向进行扩展;3(b)中的倾斜裂纹并不是沿着初始裂纹方向起裂并扩展,而是沿着基体厚度方向起裂,其扩展路径向试样中心线处靠近.同时靠近涂层-基体界面的基体裂纹在涂层-基体界面发生偏转并沿着涂层-基体界面扩展.同样,3(c)中与涂层-基体界面相平行的初始裂纹,一方面沿着基体厚度方向起裂并向靠近试样中心线的方向扩展;另一方面裂纹沿基体厚度方向朝涂层-基体界面扩展,并在涂层-基体界面发生偏转,最终沿着涂层-基体界面扩展.通过数值模拟,记录下图 3所示的三种裂纹在三点弯曲试验下裂纹发生扩展时的临界载荷,模拟得到的数据如表 5所示.

|
图 4 三点弯曲下基体内部偏置裂纹的扩展形貌 Figure 4 The entended morphology of offset cracks in the substrate under three-point bending |
| 表 5 不同裂纹扩展时的临界载荷 Table 5 Critical load of different propagation |
根据以上数据可知,当初始裂纹位置一定时,45°倾斜裂纹的裂纹扩展临界载荷大于垂直裂纹的临界载荷.当裂纹形貌一定,也就是裂纹倾斜角度一定时,结合表 4,当裂纹埋藏深度为0 mm时,模拟得到中心带有垂直裂纹试样和45°倾斜裂纹试样发生裂纹扩展时的临界载荷分别为2.42 kN和2.83 kN,偏置裂纹的裂纹扩展临界载荷大于中心线裂纹的临界载荷.以上结果表明,在该三点弯曲试样中,垂直裂纹较倾斜裂纹更为危险,裂纹越靠近试样的中心线越危险.当初始裂纹为图 3(c)所示的横向裂纹时,发生裂纹扩展的临界载荷较大,此时试样较安全.
2.2 实验结果为了验证模拟结果的正确性,对三点弯曲实验下基体裂纹的扩展行为进行实验研究.三点弯曲试验下,垂直裂纹试样的裂纹扩展形貌如图 5(a)所示,45°倾斜裂纹的试样扩展形貌如图 5(b)所示.从图中可以看出,随着载荷的增加,垂直裂纹试样中的基体裂纹一方面沿着基体厚度方向扩展,另一方面向涂层方向扩展,并沿厚度方向垂直穿透涂层,在涂层与基体界面处没有界面裂纹的出现.而45°倾斜裂纹试样中的基体裂纹,一方面在竖直方向开始起裂,向基体扩展,其扩展路径向试样中心线处靠近,另一方面在涂层与基体界面处有界面裂纹萌生,并沿着涂层-基体界面扩展,与此同时部分基体裂纹越过涂层-基体界面向涂层厚度方向扩展直至穿透涂层.实验所观察到的现象与模拟结果略有不同,模拟过程中未能实现基体裂纹越过涂层-基体界面向涂层方向扩展.这是由于运用扩展有限元法模拟裂纹扩展问题时,只能设定单一的开裂区间,即只在选定的部件中对裂纹扩展问题进行研究,当基体裂纹抵达涂层-基体界面时,采用内聚力单元(Cohesive Element)可以实现裂纹沿着涂层与基体界面的扩展,但不能实现基体裂纹越过涂层-基体界面向涂层方向扩展,这是有限元所不能达到的[21-23].并且由于基体裂纹在制备的过程中将涂层也进行了相应的破坏才得以产生,因此我们需采用模拟与实验相结合的方法对裂纹扩展行为进行观察.

|
图 5 三点弯曲试验下的裂纹扩展形貌(a)垂直裂纹试样(b) 45°倾斜裂纹试样 Figure 5 Crack propagation morphology under three-point bending test:(a)Vertical crack specimen; (b)45°inclined crack specimen |
根据加载压头上施加的载荷及压头的位移数据,绘制垂直裂纹试样和45°倾斜裂纹试样在三点弯曲试验中的施力点位移-载荷曲线,如图 6所示,曲线上突变点处的载荷大小即为裂纹开始扩展的临界载荷,最终得到弯曲试验中两种裂纹形式的试样发生裂纹扩展时的临界载荷如表 6所示.垂直裂纹试样用A表示,45°倾斜裂纹用B表示.
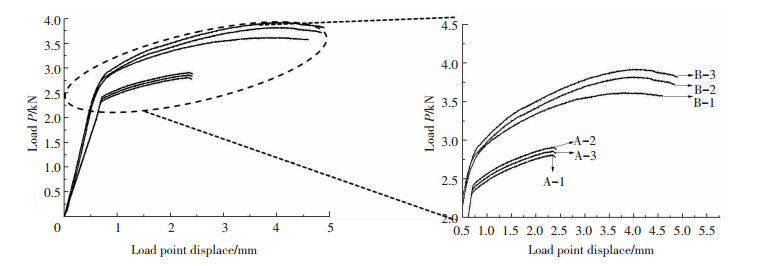
|
图 6 弯曲试验中的施力点位移-载荷曲线 Figure 6 Displacement-load curve of force point in the bending test |
| 表 6 三点弯曲试验中两种试样发生裂纹扩展时的临界载荷 Table 6 Critical load of crack propagation of the two specimens under three-point bending test |
综合图 6与表 6结果表明,基体内部初始裂纹在竖直方向投影长度相同时,垂直裂纹试样发生裂纹扩展时的临界载荷小于45°倾斜裂纹试样的临界载荷,相同条件下,垂直裂纹更加危险.同时,三点弯曲试验下垂直裂纹扩展的平均临界载荷为2.35 kN,有限元模拟得到的临界载荷为2.42 kN;而45°倾斜裂纹试样的平均扩展临界载荷为2.76 kN,有限元模拟得到的临界载荷为2.83 kN,其误差范围均在3%以内,模拟与实验结果相近,证明了模拟的正确性.
3 结论本文利用有限元法对弯曲应力作用下再制造件基体内部裂纹的扩展行为进行了数值模拟,并进一步分析基体内部裂纹形貌及裂纹埋藏深度对其裂纹扩展行为的影响,接下来对弯曲应力作用下再制造件基体内部裂纹的扩展行为进行了试验研究,得出以下结论:
1) 在三点弯曲试验下,当初始裂纹位置一定时,45°倾斜裂纹扩展的临界载荷大于垂直裂纹的临界载荷,即垂直裂纹较倾斜裂纹更为危险.
2) 当裂纹形貌一定,也就是裂纹倾斜角度一定时,偏置裂纹的裂纹扩展临界载荷大于位于中心线的裂纹扩展临界载荷,即裂纹越靠近试样的中心线越危险.
3) 当裂纹形貌一定时,随着裂纹埋藏深度的增加裂纹扩展的临界载荷逐渐增加,且当埋藏深度达到一定程度时,没有出现裂纹扩展现象.
4) 对三点弯曲试验下垂直裂纹和倾斜裂纹的扩展行为进行了实验研究,实验结果与模拟结果相同,验证了模拟了正确性.
| [1] |
徐滨士. 装备再制造工程的理论与技术[M]. 北京国防工业出版社, 2007. XU Binshi, The theory and technology of remanufacturing engineering[M]. Beijing National Defense Industry Press, 2007. |
| [2] |
张显程. 面向再制造的等离子喷涂层结构完整性及寿命预测基础研究[D]. 上海: 上海交通大学, 2007. ZHANG Xiancheng. Basic researches on the structural integrity and life prediction of plasma-sprayed coating based systems aiming for remanufacturing[D]. Shanghai: Shanghai Jiao Tong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10248-2008052214.htm |
| [3] |
成大先. 机械设计手册[M]. 北京: 化学工业出版社, 2003.
CHENG Daxian. Mechanical design manual[M]. Beijing: Chemical Industry Press, 2003. |
| [4] |
徐滨士, 董丽虹. 再制造质量控制中的金属磁记忆检测技术[M]. 北京: 国防工业出版社, 2015.
XU Binshi, DONG Lihong. Metal magnetic memory testing technology in remanufacturing quality control[M]. Beijing: National Defense Industry Press, 2015. |
| [5] | WU Y, LI W, YANG P. A study of fatigue remaining useful life assessment for construction machinery part in remanufacturing[C]// Procedia CIRP. 2015: 758-763. |
| [6] | XU R, ZHANG W X, et al. Effect of periodic surface cracks on the interfacial fracture of thermal barrier coating system[J]. Applied Surface Science, 2012, 258(24): 9816–9823. DOI: 10.1016/j.apsusc.2012.06.036 |
| [7] | DONG H, YANG G J, CAI H N, et al. Propagation feature of cracks in plasma-sprayed YSZ coatings under gradient thermal cycling[J]. Ceramics International, 2014, 41(3): 3481–3489. |
| [8] | BOUAZIA H, BRINZA O, HADDAR N, et al. In-situ SEM study of crack initiation, propagation and interfacial debonding of NiP coating during tensile tests: heat treatment effect[J]. Materials Characterization, 2017, 123: 106–114. DOI: 10.1016/j.matchar.2016.11.017 |
| [9] | VAUNOIS J R, POULAIN M, KANOUTE P, et al. Development of bending tests for near shear mode interfacial toughness measurement of EB-PVD thermal barrier coatings[J]. Engineering Fracture Mechanics, 2017, 171: 110–134. DOI: 10.1016/j.engfracmech.2016.11.009 |
| [10] | ALMEIDA G, GONZALEZ J, ROSADO L, et al. Advances in NDT and Materials Characterization by Eddy Currents[C]// Elsevier B V 2013: 7(12): 359-364. |
| [11] |
肖会芳, 徐金梧, 何飞, 等. 金属内部裂纹的超声衰减特性与近表面缺陷识别[J]. 北京科技大学学报, 2014, 36(6): 838–844.
XIAO Huifang, XU Jinwu, HE Fei, et al. Ultrasonic attenuation characteristics of metal materials with cracks and identification of subsurface fiaws[J]. Journal of University of Science and Technology Beijing, 2014, 36(6): 838–844. |
| [12] |
张辉, 李树君, 王伟平. 声发射技术在热障涂层失效机理研究中的应用[J]. 无损检测, 2010, 32(6): 409–411.
ZHANG Hui, LI Shujun, WANG Weiping. Application of acoustic emission technology in research of failure causation in thermal barrier coating[J]. Nondestructive Testing, 2010, 32(6): 409–411. |
| [13] | EGBEWANDE A, CHEN W, EADIE R, et al. Surface crack growth behavior of pipeline steel under disbonded coating at free corrosion potential in near-neutral ph soil environments[J]. Metallurgical & Materials Transactions A, 2014, 45(11): 4946–4959. |
| [14] | OKAJIMA Y, SAKAGUCHI M, INOUE H. A finite element assessment of influential factors in evaluating interfacial fracture toughness of thermal barrier coating[J]. Surface & Coatings Technology, 2017, 313: 184–190. |
| [15] | RENZELI M, MUGHAL M Z, SEBASTIANI M, et al. Design, fabrication and characterization of multilayer Cr-CrN thin coatings with tailored residual stress profiles[J]. Materials & Design, 2016, 112: 162–171. |
| [16] | NAYEBPASHAEE N, SEYEDEIN S H, ABOUTALEBI M R, et al. Finite element simulation of residual stress and failure mechanism in plasma sprayed thermal barrier coatings using actual microstructure as the representative volume[J]. Surface & Coatings Technology, 2016, 291: 103–114. |
| [17] | ZHANG B J. Ductile failure analysis and crack behavior of X65 buried pipes using extended finite element method[J]. Engineering Failure Analysis, 2014, 45(1): 26–40. |
| [18] | TED Diehl. On using a penalty-based cohesive-zone finite element approach, part Ⅰ: elastic solution benchmarks[J]. International Journal of Adhesion and Adhesives, 2007, 28(4): 237–255. |
| [19] | SORENSEN B F, TORBAN K, JACOBSEN. Characterizing delamination of fibre composites by mixed mode cohesive laws[J]. Composites Science and Technology, 2008, 69(3): 445–456. |
| [20] | ZHAO H F, CHEN M, JIN Y. Determination of interfacial properties between metal film and ceramic substrate with an adhesive layer[J]. Materials and Design, 2008, 30(1): 154–159. |
| [21] |
底月兰, 王海斗, 董丽虹, 等. 扩展有限元法在裂纹扩展问题中的应用[J]. 材料导报, 2017, 31(2): 70–74.
DI Yuelan, WANG Haidou, DONG Lihong, et al. Application of the extended finite element method in crack propagation[J]. Materials Review, 2017, 31(2): 70–74. |
| [22] | STOLARSKA M, CHOPP D L. Modeling thermal fatigue cracking in integrated circuits by level sets and the extended finite element method[J]. International Journal of Engineering Science, 2003, 41(20): 2381. DOI: 10.1016/S0020-7225(03)00217-9 |
| [23] | GRAVOUIL A, MOES N, BELYTSCHKO T. Non-planar 3D crack growth by the extended finite element and level sets-part Ⅱ:level set update[J]. International Journal for Numerical Methods in Engineering, 2002, 53(11): 2549–2568. DOI: 10.1002/nme.v53:11 |
 2018, Vol. 26
2018, Vol. 26


