2. 轧制技术及连轧自动化国家重点实验室(东北大学),沈阳 110819;
3. 安徽工业大学 冶金工程学院,安徽 马鞍山 243032
2. State Key Laboratory of Rolling and Automation(Northeastern University), Shenyang 110819, China;
3. School of Metallurgical Engineering, Anhui University of Technology, Maanshan 243032, China
轧制铜箔广泛用于制造挠性覆铜箔层压板(FCCL)及挠性印制线路板(FPC)、汽车动力与通讯设备用锂离子二次电池、节能产品LED、电子设备的散热与屏蔽等产品.随着电子、计算机、电气元件逐步向微型化及薄型化方向发展,轧制铜箔的应用领域日渐广泛,对其质量和性能也提出了更高要求.轧制铜箔的变形与成形性能是其得以广泛应用的关键,对于不同晶粒结构的轧制铜箔,轧制变形特性存在着差异.对退火态轧制铜箔的研究表明[1],其轧制变形特性与微观组织结构具有密切的关系,目前对于轧制铜箔的变形规律及机制尚不明确.
在金属箔材试样中,当晶粒尺寸大于箔材厚度时,则在箔材厚度方向上可能只分布一层晶粒,称为单层晶[2].单层晶铜箔的厚度只有几十微米,晶粒尺寸和箔材厚度在同一数量级上.极薄带轧制变形时变形区的大小与几个晶粒尺寸相当,晶粒的大小、取向、分布等微观组织结构对箔材性能、塑性变形规律、成形工艺的影响十分突出.多晶体材料宏观尺度的均匀变形在介观尺度上往往表现为非均匀性,其宏观性能是微结构敏感的,依赖于晶粒结构、晶粒取向、晶界分布、滑移系和位错组态等[3].采用实验的方法对极薄带轧制变形进行研究,需要进行大量的重复性实验,浪费时间和消耗巨大,且变形过程中箔材的变形规律及滑移特性也难以获得,而采用数值模拟的方法可大幅度提高研究效率及准确性.
常用的数值模拟方法有泰勒模型[4]和VPSC模型[5],这些模型本构关系忽略多晶体微观结构、介观不均匀性和各向异性的影响,因此不能计算晶粒内滑移系的启动特性以及晶粒间的相互作用,包括变形局部化、晶粒取向变化、滑移系启动.晶体内部的位错滑移是金属材料发生塑性变形的主要机制,晶体塑性有限元模型(CPFEM)将基于位错在滑移系上滑移而建立起来的晶体塑性本构理论与有限元理论相结合,同时考虑了各晶粒的宏观边界条件和不同晶粒间的相互作用,在构建模型过程中引入晶粒尺寸、晶粒取向以及滑移系等微观结构信息,其更接近材料变形的物理本质,被广泛用来描述晶体材料在微观变形时的性能变化.
Taylor等[6]对晶体塑性理论做了开创性的工作,通过假设晶粒间应变或应力平衡来研究材料变形的织构演化.Pierce等[7-8]对率相关晶体塑性本构理论建立了完整的数学模型并解决了其数值求解不稳定问题,为建立精确的模拟大应变变形的多晶体模型指明了方向.Molinari等[9]改进Taylor模型,将单个晶粒的变形进行平均化来研究多晶体材料的变形.晶体塑性理论和模型已广泛应用于:单晶/多晶体变形织构发展与演化分析[10-11]、微观应力应变分布分析[12-13]、变形工艺分析[14]、局部变形[15]、尺寸效应[16-19]等方面.研究者采用晶体塑性有限元模拟介观尺度下材料的微观变形、织构演化时,多将材料简化为单晶体并对其进行建模,以消除晶界的影响[20-21],没有考虑晶界对微观变形及滑移特性的影响.晶界是固体材料中的一种面缺陷,由于晶界的特殊性,使得多晶材料的塑性变形、强度、断裂、疲劳等性能与单晶材料有很大差异,晶界对变形具有阻滞作用及进行多系滑移,晶粒结构及晶界组态对晶内-晶界滑移特性和材料微观变形机制有很大影响.很多研究所设定的压下率小于50%,而采用晶体塑性有限元模拟压下率大于50%时的微观变形及织构演化的研究工作很少.以上工作在一定程度上研究了介观尺度下单晶体/多晶体材料微观变形及织构演化规律,但缺乏晶界组态对极薄带轧制局部滑移特性影响的深入考察.
本文采用晶体塑性有限元模型对轧制单层晶铜箔晶界滑移特性进行模拟分析,所建晶体塑性模型考虑了潜在硬化和晶格旋转的影响,研究不同轧制压下率(40%,60%,80%)对轧制单层晶铜箔晶界滑移系激活特性、晶体取向及局部变形的影响规律.对此的研究可以在较深层次上揭示轧制单层晶极薄带时晶界的微观作用机制.
1 晶体塑性有限元模型采用Peirce[8]提出的率相关晶体塑性滑移理论,考虑晶格旋转和潜硬化,采用切线系数法将其嵌入ABAQUS/Standard-6.13.1有限元软件UMAT子程序中.
晶体弹塑性变形的变形梯度基于极分解定理可分解为位错沿滑移系滑移的塑性变形和晶格畸变与旋转的弹性变形两部分,如图 1所示.
| $ \mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{F}}^{\rm{e}}} \cdot {\mathit{\boldsymbol{F}}^{\rm{p}}}. $ | (1) |

|
图 1 晶体变形梯度的乘法分解 Figure 1 Multiplicative decomposition of deformation gradient |
式中,Fe为晶格畸变和旋转引起的变形梯度张量,Fp为位错沿特定滑移系滑移引起的变形梯度张量.假设第α滑移系的滑移方向和滑移面法向可以用2个正交的单位向量sα和mα表示,则
| $ {\mathit{\boldsymbol{\dot F}}^{\rm{p}}} = {\mathit{\boldsymbol{L}}^{\rm{p}}} \cdot {\mathit{\boldsymbol{F}}^{\rm{p}}}, $ | (2) |
| $ {\mathit{\boldsymbol{L}}^{\rm{p}}} = {\mathit{\boldsymbol{\dot F}}^{\rm{p}}}{\left( {{\mathit{\boldsymbol{F}}^p}} \right)^{ - 1}} = \sum\limits_{\alpha = 1}^N {{{\dot \gamma }^\alpha }{\mathit{\boldsymbol{s}}^\alpha } \otimes {\mathit{\boldsymbol{m}}^\alpha }.} $ | (3) |
式中,
为量化滑移剪切率
| $ {\dot \gamma ^\alpha } = \dot \gamma _0^\alpha {\left| {\frac{{{\tau ^\alpha }}}{{\tau _c^\alpha }}} \right|^n}{\rm{sgn}}\left( {{\tau ^\alpha }} \right). $ | (4) |
式中:
| $ \dot \tau _c^\alpha = \sum\limits_{\beta = 1}^N {{h_{\alpha \beta }}\left| {{{\dot \gamma }^\beta }} \right|.} $ | (5) |
式中:晶体的自硬化(α=β)和潜硬化(α≠β)行为通过硬化模量hαβ来描述,hαβ为γ的函数:
| $ \left\{ \begin{array}{l} {h_{\alpha \alpha }} = \left[ {\left( {{h_0} - {h_s}} \right){\rm{sec}}{{\rm{h}}^2}\left( {\frac{{\left( {{h_0} - {h_s}} \right){\gamma ^\alpha }}}{{{\tau _1} - {\tau _0}}}} \right) + {h_s}} \right] \times \\ \;\;\;\;\;\;\;\;\;\left[ {1 + \sum\limits_N {{f_{\alpha \beta }}{\rm{tanh}}\left( {\frac{{{\gamma ^\beta }}}{{{\gamma _0}}}} \right)} } \right]\left( {\alpha =\beta } \right), \\ {h_{\alpha \beta }} = q{h_{\alpha \alpha }}\left( {\alpha \ne \beta } \right). \end{array} \right. $ | (6) |
式中:γ0为参考剪切应变; γ为累积剪切应变;h0为初始硬化率; hs为易滑移阶段硬化模量; τ0为初始临界分剪切应力; τ1为临界分剪切应力饱和值; q为潜硬化系数与自硬化系数之间的比值; fαβ表示滑移系α与滑移系β间的相互作用系数,其大小取决于滑移系的几何关系,由5个常数ai来表示.
在数值计算时,采用切线系数增量法求解,将式(4)改写成:
| $ \Delta {\gamma ^{\left( \alpha \right)}} = \left[ {\left( {1 - \theta } \right){{\dot \gamma }^{\left( \alpha \right)}}\left( t \right) + \theta {{\dot \gamma }^{\left( \alpha \right)}}\left( {t + \Delta t} \right)} \right]\Delta t. $ | (7) |
纯铜为FCC晶体结构,位错滑移发生在滑移系{1 1 1} <1 1 0>上,其滑移面和滑移方向如表 1所定义.纯铜弹性模量为C11= 168.4 GPa, C12= 121.4 GPa, C44=75.4 GPa,其滑移系相互作用系数fαβ可表示为a1=a2=a3=8,a4=15,a5=20[22].
| 表 1 晶体塑性模型中所用滑移系定义 Table 1 Definition of slip systems (SS) used in the model |
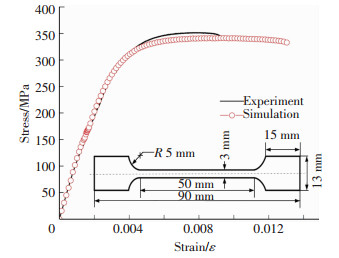
本工作在设定的材料参数下模拟拉伸变形,并与实验对比,选取合适的本构参数.模拟条件:铜箔厚度125 μm,拉伸速度0.05 mm/min,赋予5种不同随机晶粒取向.经过多次模拟验证后得到的参数如表 2所示,实验与模拟得到的应力-应变曲线对比如图 2所示,结果吻合较好.
| 表 2 纯铜的本构参数 Table 2 Constitutive parameters of pure copper |
|
图 2 纯铜在模拟和实验条件下应力-应变曲线对比 Figure 2 Comparison of the simulated and experimental stress-strain curves |
将极薄带轧制简化为平面应变变形,取轧制方向(RD)作为X轴,法向(ND)作为Y轴,横向(TD)作为Z轴,轧制示意图及坐标设定如图 3(a)所示.计算模型尺寸为3 mm ×0.1 mm,采用修正Voronoi图的多晶模型重构初始晶粒形貌,平均晶粒尺寸d=100 μm,即铜箔厚度方向只有一层晶粒(单层晶).经完全退火后,纯铜极薄带晶粒取向随机分布,赋予轧制铜箔初始晶粒{111}极图如图 3(b)所示.模拟过程中,轧辊和铜箔均设置为变形体,采用CPE4R单元离散单层晶极薄带模型,每个晶粒包含100个单元.

|
图 3 (a) 极薄带轧制示意图及坐标轴设定;(b)初始单层晶极薄带晶粒{111}极图 Figure 3 (a) Schematic illustration of foil rolling process and the coordinate system. (b) {111} pole figure of initial crystallographic orientation |
模拟单层晶铜箔轧制工艺参数如下:上下工作轧辊直径为30 mm,上轧辊转速为1.04 rad/s,上下轧辊异速比为1.1,轧辊与轧件之间接触采用库仑摩擦,摩擦系数为0.1,道次压下率分别为40%,60%和80%.
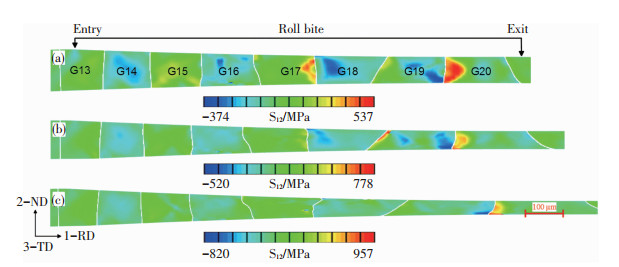
3 模拟结果与讨论图 4显示压下率为40%,60%和80%时轧制变形区的切应力分布.变形区微观切应力的分布反映出沿轧制方向和铜箔厚度方向变形的非均匀性,可见变形非均匀程度和切应力大小随压下率的增加而增大.变形区内各晶粒中心网格的畸变程度明显小于边部网格,单层晶铜箔原来垂直表面的晶界,经过轧制变形后发生了扭转和弯曲,且随压下率的增加而程度明显增大.晶界和晶内存在应力集中区,具有明显的应力梯度现象,随着压下率的增加,应力集中区向晶界处移动,且应力最大值主要分布在晶界.在大压下轧制时,晶界处的应力集中现象是由晶界两侧晶粒取向差增大且处于硬取向状态,滑移系启动所需临界切应力增大,滑移面转动导致应力集中.
|
图 4 不同压下率时轧制变形区切应力分布 Figure 4 Distribution of shear stress in the deformation zone during cold rolling with reduction of(a)40%, (b)60%, and(c)80% |
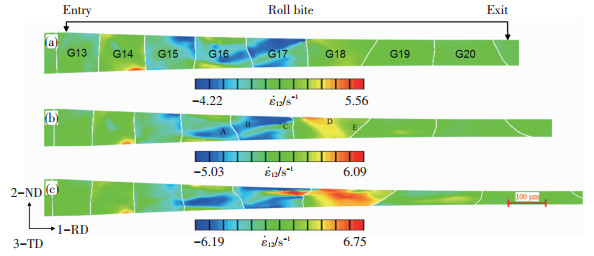
图 5显示压下率为40%,60%和80%时轧制变形区的切应变率分布.由图可知,晶内-晶间应变率分布呈现严重的不均匀性,应变率随压下率的增加而增大,出现贯穿整个晶粒的剪切带及变形局部化现象,当压下率为40%时,剪切带与轧制方向呈45°,夹角随压下率增加而减小,当压下率达到80%时,剪切带与轧制方向平行,如G16和G17内形成贯穿晶粒的剪切带,G18在压下率大于60%时出现贯穿晶粒且与轧制方向呈-45°的剪切带,在剪切带之间出现非变形区,当压下率达到80%时,沿晶粒厚度方向出现方向相反交错排列的剪切带,个别晶粒发生了较大的塑性变形,而有的晶粒及晶粒内部变形较小,如A,C和D处的切应变率值差异较大,这是由部分晶粒处于择优取向而发生较大变形,变形较大处的滑移运动易受到晶界阻碍作用而减弱,晶粒内部位错滑移所受阻碍较小,导致晶间-晶内变形出现局部化现象,且随压下率增加而更显著.
|
图 5 不同压下率时轧制变形区切应变率分布 Figure 5 Distribution of shear strain rate in the deformation zone during cold rolling with reduction of(a)40%, (b)60%, and(c)80% |
图 6显示压下率为40%,60%和80%时相邻晶粒16,17和18轧制变形前后{111}极图的对比,图中青色实体方框表示各晶粒的初始取向.由图可知,轧制变形后各晶粒的取向绕TD方向发生了明显地转动,同一晶粒内部不同区域的转动情况有较大差异,转动角度随压下率的增加而显著增大,当压下率达到80%时,最大转动角度可达60°,当压下率小于40%时,各晶粒取向极点只在初始取向附近产生很小的分散,但当压下率达到60%以上时,变形后晶粒取向极点沿TD方向顺时针和逆时针扩散很大角度,各晶粒变形后取向极点除沿TD方向转动较大角度外,还沿RD和ND方向进行偏移,晶粒16和17变形后取向极点沿TD方向的转动角度和极点分散度明显大于晶粒18,这是晶粒16和17的初始取向处于软状态,易于首先进行滑移而发生变形,因此在晶粒16和17内形成贯穿晶粒的滑移带及发生较大变形,晶界发生明显变形,晶粒18初始取向处于硬状态,压下率小于60%时,变形后晶粒18取向极点仅仅沿TD方向转动很小角度且取向变化很小,但压下率达到80%时,变形后晶粒18取向极点沿TD方向转动很大角度且极点分散度显著增大,可见初始处于硬取向状态的晶粒18只有在大压下率轧制变形时才会发生协调变形.因此当单层晶极薄带采用大压下轧制时,在晶内可产生更多的剪切带,易于促进协调变形.

|
图 6 不同压下率时晶粒16、17和18轧制变形前后{111}极图对比 Figure 6 {111} pole figures of G16, 17 and 18 before and after rolling deformation with reductions of (a) 40%, (b) 60%, and (c) 80% |
图 7为轧制单层晶极薄带变形过程中特殊位置处启动滑移系的状态,位置D处于晶粒18的上表层,位置E处于晶界(如图 5(b)中所标注),可见晶粒内不同位置的滑移系启动情况和滑移状态是不一样的且受轧制压下率的影响较大,启动滑移系的滑移程度随压下率的增加而增大.当压下率低于60%时,在晶粒表层和晶界处,滑移系成对启动,两处开动滑移系的数目都是4个,其中d3沿正方向进行滑移,而a3,b1和b3则沿负方向进行滑移,b1和b3滑移系的滑移剪切率首先达到临界值而启动,随轧制过程的进行,由于b1和b3的运动,导致晶格发生转动,使a3和d3处于软取向状态而被激活;当压下率达到80%时,D处启动滑移系7个,E处启动滑移系5个,两处呈现多系滑移状态,b1和b3在D处首先激活开动,随轧制过程的进行,新滑移系c3被激活,a3和d3在c3停止滑移时被激活开动,在轧制变形的最后阶段,新滑移系d1被激活,同时c3被重新激活运动且滑移方向发生改变,b1和b3在E处首先激活开动,随轧制过程的进行,a3,d1和d3被激活运动,但d1很快就停止运动了,表明其运动程度较小;晶界E处启动滑移系的滑移剪切率波动程度明显大于晶粒表层且随轧制压下率的增加而波动程度增大,这是由晶界两侧晶粒的取向差及晶粒间相互的复杂作用导致晶界处启动滑移系运动程度波动较大;由此可知,轧制单层晶极薄带变形非均匀性、局部化及晶粒取向演化与滑移系开动状态有密切关系,单层晶结构、晶粒取向差、晶粒间相互作用(晶界)会导致轧制变形时滑移系激活与运动的差异性.

|
图 7 不同压下率时特殊位置D、E处启动滑移系情况(图 5(b)中标注) Figure 7 Activated slip systems at position D and E for reduction of (a) 40%, (b) 60%, and (c) 80% |
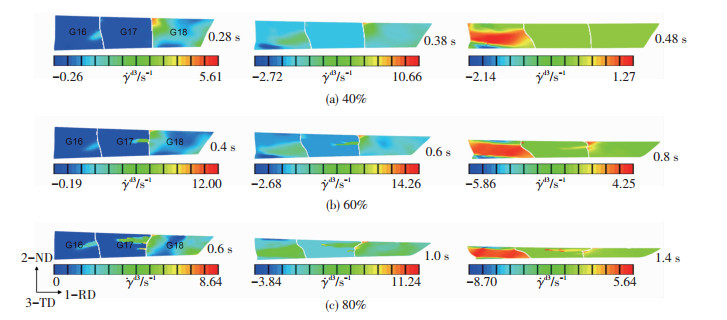
图 8显示压下率为40%,60%和80%时滑移系b3的滑移剪切率演化云图,可见滑移系在不同晶粒及同一晶粒内运动的差异性,b3在3个晶粒内都被激活运动,形成了明显的滑移带,在G16和G18中沿负方向进行滑移,在G17中沿正方向进行滑移,滑移带之间存在非滑移区,表明晶粒内部分区域滑移系b3并没有被激活,其他区域滑移系虽被激活,但其滑移程度较小,另外,滑移主要发生在剪切变形带上,晶界和晶粒表层处滑移系b3的开动程度很显著,当压下率小于60%时,晶粒内部形成的滑移带与轧制方向呈±30°~±45°的夹角,当压下率达到80%时,滑移带与轧制方向平行,滑移运动扩展到整个晶粒,晶内滑移带增多且出现滑移方向的交替变化现象,滑移系b3首先在晶界和晶粒表层处被激活,随轧制过程的进行,形成滑移带并逐渐向晶内扩展;图 9显示压下率为40%,60%和80%时滑移系d3的滑移剪切率演化云图,可见滑移系d3在晶内的滑移状态与b3有较大的差异,当压下率小于60%时,d3并没有在个别晶粒内被激活,其他区域虽被激活,但滑移程度很小,当压下率达到60%以上时,d3在晶内形成了与轧制方向平行的滑移带,当压下率达到80%时,在晶内形成了滑移方向正负相反的滑移带,且滑移带增多,晶内滑移扩展区增大,滑移系d3首先在晶界处被激活,然后向晶内扩展;以上对滑移系b3和d3的滑移运动分析可知,轧制单层晶极薄带时,采用大压下轧制可以促进滑移系的启动与运动,更易增大晶内滑移扩展区,晶内滑移带个数增多,滑移系更易在晶界和单层晶晶粒表层被激活,然后逐渐向晶粒内部进行滑移扩展.对比轧制变形区剪切应变率云图与滑移系运动状态云图可知,随晶内滑移带的增多,晶内剪切变形带亦增多且出现方向相反的剪切变形现象,剪切变形增强.

|
图 8 不同压下率时滑移系b3的滑移剪切率演化情况 Figure 8 Slip shear rate evolution along active slip system b3 of G16, 17 and 18 with reductions of (a) 40%, (b) 60%, and (c) 80% |
|
图 9 不同压下率时滑移系d3的滑移剪切率演化情况 Figure 9 Slip shear rate evolution along active slip system d3 of G16, 17 and 18 with reductions of (a) 40%, (b) 60%, and (c) 80% |
图 10为加热温度920 ℃,保温时间7 h退火后铜箔的显微组织,可知经退火后100 μm厚铜箔试样厚度方向只有一层晶粒,即获得了单层晶.

|
图 10 退火后铜箔的显微组织 Figure 10 Microstructure of the annealed pure copper foil |
采用课题组自主设计研制的四辊微成形轧机(3M轧机)进行箔轧实验,压下率40%和60%,异速比1.1,前后张力各为100 MPa,对每一压下率进行多次箔轧,取平均单位宽度轧制力与模拟结果对比,如表 3所示,可知模拟和实测轧制力都随压下率的增加而增大,且具有较好的吻合性.
| 表 3 模拟和实测的平均单位宽度轧制力对比 Table 3 Comparison beteen Simulated and measured average wnit width rouing forces |
1) 在晶间-晶内均出现变形非均匀性,并出现剪切带和变形局部化现象,这主要是由单层晶结构特征、晶粒取向差及晶界滑移特性造成的.
2) 晶间复杂的相互作用及晶界滑移特性引起晶粒取向主要绕横向发生旋转,且旋转角度和取向极点分散度随压下率的增加而增大.
3) 滑移系启动与单层晶结构及取向密切相关,不同晶粒及晶内不同区域的滑移系激活状态存在显著差异.当压下率低于60%时,在晶粒表层和晶界处,滑移系成对发生启动,当压下率达到80%时,表层和晶界处为多滑移系启动情形.
4) 滑移剪切率沿单层晶极薄带厚度方向分布不均匀,存在明显的梯度波动现象,在滑移带之间存在非滑移区,滑移首先在晶粒表层和晶界处开始,然后向晶内延伸.
5) 随着轧制压下率的增加,启动滑移系数目及晶内滑移带增多,滑移带之间的交互作用及剪切变形增强,在晶内某些区域,只有部分滑移系被激活且滑移程度较弱.
| [1] |
刘雪峰, 李晶琨, 汪汐涌, 等. 压延铜箔轧制压下率与组织织构和耐弯折性能的关系[J]. 材料研究学报, 2014, 28(4): 241–247.
LIU Xuefeng, LI Jingkun, WANG Xiyong, et al. Relations of rolling reduction and microstructure, texture and bending property of rolled copper foils[J]. Chinese Journal of Materials Research, 2014, 28(4): 241–247. |
| [2] | CHEN S D, LIU X H, LIU L Z. Symmetric and asymmetric rolling pure copper foil: crystal plasticity finite element simulation and experiments[J]. Acta Metallurgica Sinica (English letters), 2015, 28(8): 1024–1033. DOI: 10.1007/s40195-015-0290-0 |
| [3] |
赵蒙, 李萍, 李成铭, 等. TA15钛合金高温变形过程的介观模拟计算[J]. 稀有金属材料与工程, 2015, 44(4): 927–932.
ZHAO Meng, LI Ping, LI Chengming, et al. Mesoscale simulation on plastic deformation of TA15 titanium alloy at high temperature[J]. Rare Metal Materials and engineering, 2015, 44(4): 927–932. |
| [4] | LEBENSOHN R A, TOME C N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: application to zirconium alloys[J]. Acta Metallurgica et Materialia, 1993, 41(9): 2611–2624. DOI: 10.1016/0956-7151(93)90130-K |
| [5] | LI S, KALIDINDI S R, BEYERLEIN I J. A crystal plasticity finite element analysis of texture evolution in equal channel angular extrusion[J]. Materials Science and Engineering A, 2005, s410-411(12): 207–212. |
| [6] | TAYLOR G I, FRS M A. Plastic strain in metals[J]. Journal of the Institute of Metals, 1938, 62(5): 307–324. |
| [7] | PERICE D, ASARO R J, NEEDLEMAN A. An analysis of nonuniform and localized deformation in ductile single crystals[J]. Acta Metallurgica, 1982, 30(6): 1087–1119. DOI: 10.1016/0001-6160(82)90005-0 |
| [8] | PERICE D, ASARO R J, NEEDLEMAN A. Material rate dependence and localized deformation in crystalline solids[J]. Acta Metallurgica, 1983, 31(12): 1951–1976. DOI: 10.1016/0001-6160(83)90014-7 |
| [9] | MOLINARI A, CANOVA G R, AHZI S. A self consistent approach of the large deformation polycrystal viscoplasticity[J]. Acta Metallurgica, 1987, 35(12): 2983–2994. DOI: 10.1016/0001-6160(87)90297-5 |
| [10] | TAMIMI S, CORREIA J P, LOPES A B, et al. Asymmetric rolling of thin AA-5182 sheets: Modelling and experiments[J]. Materials Science and Engineering: A, 2014, 603(17): 150–159. |
| [11] | RAWAT S, CHANDRA S, CHAVAN V M, et al. Integrated experimental and computational studies of deformation of single crystal copper at high strain rates[J]. Journal of Applied Physics, 2014, 116(21): 134–138. |
| [12] | LI L, SHEN L M, PROUST G, et al. Three-dimensional crystal plasticity finite element simulation of nanoindentation on aluminium alloy 2024[J]. Materials Science and Engineering: A, 2013, 579(9): 41–49. |
| [13] | ZHANG X, AIFANTIS K E, NGAN A H W. Interpreting the stress-strain response of Al micropillars through gradient plasticity[J]. Materials Science and Engineering: A, 2014, 591(4): 38–45. |
| [14] | LIU M, TIEU A K, LU C, et al. A crystal plasticity study of the effect of friction on the evolution of texture and mechanical behaviour in the nano-indentation of an aluminium single crystal[J]. Computational Materials Science, 2014, 81(2): 30–38. |
| [15] | TURNER T J, SHADE P A, SCHUREN J C, et al. The influence of microstructure on surface strain distributions in a nickel micro-tension specimen[J]. Modelling and Simulation in Materials Science and Engineering, 2013, 21(1): 015002. DOI: 10.1088/0965-0393/21/1/015002 |
| [16] | CHEN Y, KRAFT O, WALTER M. Size effects in thin coarse-grained gold microwires under tensile and torsional loading[J]. Acta Materialia, 2015, 87(4): 78–85. |
| [17] | XU Z T, PENG L F, FU M W, et al. Size effect affected formability of sheet metals in micro/meso scale plastic deformation: Experiment and modeling[J]. International Journal of Plasticity, 2015, 68(5): 34–54. |
| [18] | LI W T, FU M W, WANG J L, et al. Grain size effect on multi-stage micro deep drawing of micro cup with domed bottom[J]. International Journal of Precision Engineering and Manufacturing, 2016, 17(6): 765–773. DOI: 10.1007/s12541-016-0094-9 |
| [19] | XIE H B, MANABE K, FURUSHIMA T, et al. An experimental and numerical investigation on micro rolling for ultra-thin strip[J]. International Journal of Material Forming, 2016, 9(3): 405–412. DOI: 10.1007/s12289-015-1229-8 |
| [20] | DENG G Y, TIEU A K, SI L Y, et al. Influence of cold rolling reduction on the deformation behaviour and crystallographic orientation development[J]. Computational Materials Science, 2014, 81(1): 2–9. |
| [21] |
毛焕泽, 温志勋, 王佰智, 等. 晶体随机取向对单晶切口试样尖端滑移特性的影响[J]. 稀有金属材料与工程, 2014, 43(11): 2743–2747.
MAO Huanze, WEN Zhixun, WANG Baizhi, et al. Effect of randomness orientation on crystal slipping around notch in single crystal superalloy[J]. Rare Metal Materials and Engineering, 2014, 43(11): 2743–2747. |
| [22] | HUANG Y G. Division of Engineering and Applied Science[D]. Harvard University, CB, 1991. https://versus.com/en/division-of-engineering-and-applied-science |
 2018, Vol. 26
2018, Vol. 26


