金属-氢系统的研究已有百年的历史,在推进材料在航空航天、新能源等领域的技术应用方面具有广泛影响.氢作为宇宙中质量最轻,含量最多的元素,在自然界中具有多种存在形式,如氢气和氢化物等.其与金属的相互作用具有正反两个方面:一方面,由于氢非常敏感而极易与金属反应,发生氢脆,导致材料断裂,而被作为有害元素;另一方面,氢又具有极其重要的利用价值,如热氢处理技术的应用,可以很好地提高金属材料的工艺性能,而且金属是一种有效的储氢材料,对促进氢能的广泛应用具有极高的价值.针对金属氢脆问题的研究已经持续了数百年,但对于氢脆的具体机理至今尚未得到统一定论,制约了氢脆问题的解决,目前仍是科学家们的研究热点.如果合理利用并控制氢在金属晶体中的含量及存在形式,则可以提高金属塑性,或将金属作为储氢材料.热氢处理技术正是利用氢在合金中的可逆合金化作用,来控制合金微观结构和提高最终的机械性能.高性能储氢材料的研发是使氢能利用推向实用化、产业化的关键,金属储氢材料是目前研究较为广泛的储氢材料,金属氢化物的储氢量和氢原子在其中的吸收率取决于金属-氢之间的成键作用.因此,为了优化材料的储氢性能及研发新型储氢材料,必须明确材料的储氢机理.过渡金属在各种有关氢的催化反应问题的研究中应用很广泛,可以通过金属催化生产氢气,深入理解相应催化过程,对解决实际工业催化问题具有指导意义.为解决这些问题,需要从微观上探究氢与金属的相互作用.
氢的原子半径非常小,很难完全通过实验方法进行研究,而计算模拟技术则可以基于实验之上更深入地研究氢致塑性微观机理、氢脆机理、储氢机理、过渡金属催化氢机理.第一性原理是电子层次上的计算方法,其可靠性高且应用范围广,既可以做已知材料的计算模拟,还可以设计具有特定性能材料,在材料计算学中具有极高价值.自上世纪90年代开始,第一性原理已被应用于研究杂质对原材料的影响,而后亦有大量学者利用第一性原理对金属-氢系统进行研究,并与实验对比,证明了第一性原理计算的准确性.
1 第一性原理简介第一性原理计算是以量子力学为基础的电子层次的计算方法,包括从头算和密度泛函理论两大类.密度泛函理论将多电子问题转化为单电子问题,较从头算方法简化了计算过程,又保证了计算的精度,是目前计算固体、分子、原子、电子结构和总能量的重要方法,在多粒子系统基态性质研究方向具有极高价值.
第一性原理计算方法根据系统中原子的数目和类型可计算出材料的晶体结构、弹性模量、能量、电荷密度、态密度、能带等性质;根据材料能量可分析材料的稳定性;根据弹性常数、模量等可分析材料的塑性、韧性、强度、硬度等力学性能;还可以研究氢原子在金属表面的吸附、体格扩散、表面能及层错能等.与真实实验相比,第一性原理计算不但能更快地设计出符合要求的实验,还可以弥补真实实验的不足,获得目前的实验和条件无法测得的性质.例如,真实实验有着难以具体描绘复杂反应过程,难以精确得到极端条件(高压、高温等)下的材料结构与物理性质,及成本高等局限性,而第一性原理计算模拟则可以很好地解决这些问题.
目前可采用不同的软件程序来实现第一性原理计算.常用软件主要有:Materials Studio,Gaussian,VASP,PWscf,Wien2k,ABINIT.
2 第一性原理在金属-氢中的应用 2.1 氢在金属中的溶解计算材料的构型及结构参数(键长和键角、原子位置、晶格常数等)对材料的力学性质影响很大.金属-氢晶体中氢原子主要以固溶氢原子、金属氢化物两种形式存在.固溶氢原子出现于当氢在金属中含量小于该温度下的最大固溶度时,氢原子由于半径很小(r=0.079 nm)会优先占据在晶体间隙位置,造成晶格畸变并膨胀.当氢含量继续增大,超过极限固溶度,金属继续吸收氢原子就会形成金属氢化物.在计算模拟中,建立准确的的金属-氢晶体结构模型的首要前提是确定氢在金属晶体中的占位,然后才能计算各种性质.目前确定氢原子占位方法主要是通过比较金属-氢晶体的晶格畸变程度和能量高低,并进一步从微观上分析金属-氢晶体的电子结构.
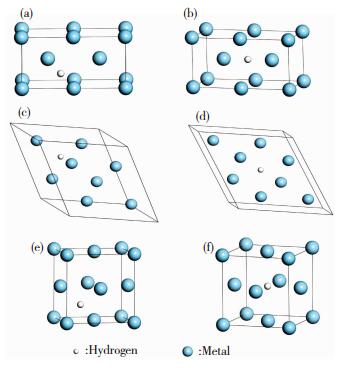
2.1.1 金属-氢晶体结构首先构建金属-氢晶体结构模型,然后通过第一性原理计算研究晶体结构的变化,图 1所示为氢占据在bcc、hcp及fcc金属晶格的四面体及八面体间隙时的结构模型.
|
图 1 金属-氢晶体结构模型 Figure 1 Structure models of Metal-Hydrogen |
韩秀丽等[1]采用第一原理计算程序CASTEP,得到氢占据不同间隙位置时α-Ti—H和β-Ti—H的晶体结构.研究发现,氢的加入导致晶格发生畸变、晶格常数及夹角都发生变化.而且,晶格畸变程度及体积膨胀率随氢含量增加而增大,且位于八面体间隙时氢导致的体积膨胀率要小于四面体间隙.张凤春[2]等人对Fe—H晶体结构研究也得到类似结论,并对H,Fe原子间距进行探讨.尽管α-Fe中四面体间隙半径大于八面体间隙,但氢在八面体间隙的体积膨胀率要小于四面体间隙.这是因为当氢原子处于α-Fe八面体间隙位置时,尽管晶格常数c值增大,但由于a,b值减小,使得体积膨胀率反而小于氢位于四面体间隙,总的点阵畸变也小于四面体间隙位置.法国学者Domain等[3]基于密度泛函理论研究了α-Zr—H系统,发现其晶体结构变化与α-Ti—H类似,但畸变程度小于α-Ti—H,印证了晶格常数越大,畸变程度越小的结论.
表 1为bcc、hcp、fcc的3种晶格结构的间隙大小,表 2为不同金属在各种氢含量下的体积膨胀率.综合表 1、表 2可以看出:一定氢浓度范围下,氢浓度越高造成的体积膨胀率越大;同样的晶格结构下,晶格常数越大,氢原子造成的体积膨胀率越小;在密排六方和面心立方结构下,八面体间隙膨胀率小于四面体间隙,是因为间隙半径越大,体积膨胀率越小.而在体心立方金属中,间隙是不对称的,不服从以上规律,使得氢原子位于半径大的四面体间隙时的体积膨胀率反而大于半径小的八面体间隙,且膨胀率高于密排六方和面心立方晶格,但当氢含量继续增大时,bcc结构中氢原子占据八面体间隙引起的体积膨胀率有可能超过四面体间隙.
| 表 1 不同晶格结构的间隙(r为金属原子半径)[4] Table 1 Interstice of different crystal structures (r is radius of metal atomic)[4] |
外界环境中的氢气首先吸附到金属表面,部分分解成氢原子,再扩散进入晶体内部,形成固溶体.氢在金属中的溶解热就是氢由气态后固溶到金属中发生的能量变化.溶解热越小,晶体结构越稳定,可以此来判断氢原子占位.可由下式计算:
| $ \Delta {H_{{\text{sot}}}} = {E_{{\text{tot}}}} - {E_{{\text{Me}}}} - \frac{1}{2}{E_{{{\text{H}}_{\text{2}}}}}. $ |
式中:Etot为晶体总能量;EMe,EH2分别为金属单质、H2能量.
Domain等[3]计算得出氢在α-Zr四面体间隙的溶解热近似为-0.60 eV,与实验结果近似,较八面体间隙溶解热小,得出氢原子占据四面体间隙的结论,并研究了相同氢含量的不同氢化物相的稳定性.氢在其他hcp结构中(Sc、Y、Er、V等)的占位也是如此,但在α-Ti中则不同,氢原子占据其八面体间隙位置.以上所列举金属中氢的溶解热皆为负值,说明氢在这些金属中的溶解属于放热反应.而美国加利福尼亚大学的Jiang[6]教授等应用密度泛函理论计算的氢在α-Fe四面体间隙中的溶解热为0.2 eV左右.国内学者也对此进行了研究[2],发现氢在γ-Fe中的溶解热也为正值,表明氢原子的溶解需要吸收能量,不容易固溶于α-Fe、γ-Fe晶体中,与相关实验结果一致.
表 3所示为氢在部分金属中的溶解热,可以看出:氢在多数金属中的的溶解热为负,说明氢很容易溶解在金属中.
在多数hcp、bcc金属中,氢在四面体间隙的溶解热要比处在八面体间隙小,说明氢倾向于溶解在四面体间隙位置,但也有例外.有研究表明电荷密度、H—H之间的相互作用、H周围原子都影响到溶解热[12].
还有学者研究了空位、杂质等缺陷对氢在金属中溶解热的影响.如:有研究表明空位的存在降低了氢在Mo中的溶解热[13],W中氢的加入能够诱导空位的产生,且这种诱导作用随氢浓度增加而增强[14],这对金属中氢气泡形成起到了很好的解释作用.氢在V-Ti-Cr合金中会受到Ti的吸引,Cr的排斥,占据靠近Ti的四面体间隙位置时有较小的溶解热,更为稳定[15].NiAl合金中,氢占据在富Al的八面体间隙和Ni3Al中Ni原子构成的八面体间隙位置时,溶解热小[16].可见,空位、杂质对氢在金属中的溶解热有着不可忽视的影响,但对于一些大的缺陷会造成的影响则鲜有研究.
2.1.3 金属-氢系统的电子结构电子结构决定了原子间的成键、离化程度,并影响到材料的结构,继而影响其性能.国内很多学者利用第一性原理计算了金属-氢系统的能带结构、态密度、电荷布居以及电荷差分密度,对氢原子于金属晶体电子结构的影响进行了研究.
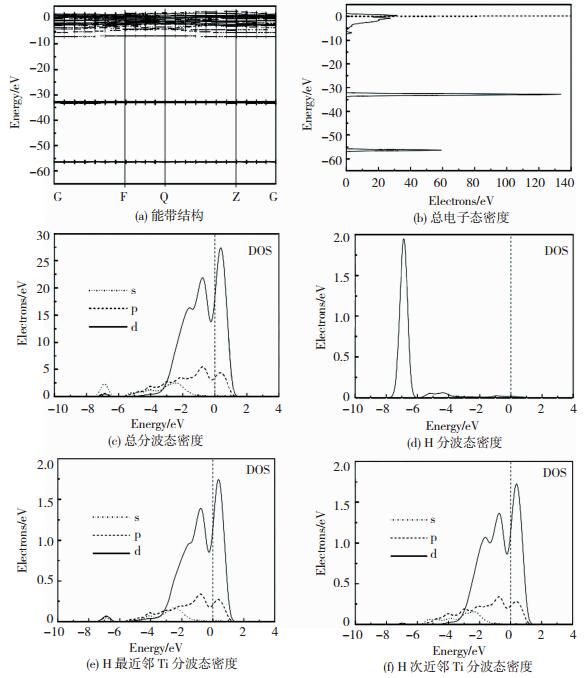
图 2为氢占据α-Ti—H(16Ti+1H)的八面体间隙位置时的能带结构及电子态密度[17].图 2(a)显示价带和导带之间没有带隙,因此,体系仍是金属属性;但在费米面以下有一条新的能带产生,同相邻能带之间形成的带隙宽度约为2 eV,是激发孤立带上的电子加入自由电子活动所需的最小能量值.
|
图 2 α-Ti—H晶体的能带结构和电子态密度[17] Figure 2 Energy band structure and DOS of α-Ti—H crystal[17]: (a)energy band structure; (b) total DOS; (c) total partial DOS; (d) H partial DOS; (e) partial DOS of Ti atom which is the nearest neighbor of H atom; (f) partial DOS of Ti atom which is the next nearest neighbor of H atom |
对比图 2(d)、(e)和(f)发现,新能带的产生主要是H与近邻Ti原子之间的作用,氢改变了近邻Ti原子的电子态密度,但远处的Ti原子电子态密度变化很小,说明氢的作用具有局域性.
原子间键重叠集居数高时,键的共价性强,集居数低时原子间键则偏离子性.在α-Ti—H中,氢原子的加入使其周围钛原子间的键重叠集居数减小,减弱了成键强度,具有弱键效应;而在β-Ti—H中,氢的加入使周围钛原子间的键重叠集居数增加,具有强键效应.对Nb—H[18]、Zr—H[19]体系电子结构的研究也发现类似Ti—H晶体的变化.氢原子加入到六方相α-Fe2O3晶体时,氢原子和氧原子之间会成键,新的杂化能级在费米面附近出现,价带顶被拓宽,导带底下移而使带隙减小,表明氢原子有调节能带结构的作用[20].
2.2 氢在金属中的的吸附及扩散在具有氢气的外界条件下,氢气分子与金属表面碰撞,通过物理吸附留在金属表面.部分氢分子解离成原子氢并与金属表面产生化学吸附.解离后的氢原子迁移到金属晶体内部的空位或间隙,形成置换固溶体或间隙固溶体.随氢原子增加,氢浓度或温度不均匀导致氢原子在金属晶格间隙间扩散,逐渐使浓度或温度趋于均匀.
2.2.1 氢在金属表面的吸附氢和金属表面的相互作用在气体-表面反应中占有极其重要的地位,针对氢在金属表面的吸附、扩散问题已有广泛研究,对于探讨多相催化机理、原子-金属表面间相互作用都有重要意义.很多学者应用第一性原理对氢在金属表面的吸附位置、路径、稳定性等都做了研究.
国内外学者[21-22]的研究表明,氢在Fe(111)、Fe(100)和Fe(110)的3个晶面上稳定吸附,相互作用较强,在晶面上发生扩散,并发现覆盖度会影响吸附位置而对吸附过程及氢与金属表面之间的作用力无明显影响.其他研究也发现氢的吸附位置与覆盖度有关.例如,在Pd(100)面,覆盖度θ < 1时氢原子会吸附到四重洞位,θ>1时,额外的氢原子吸附到次表面或占据桥位,并很可能扩散到体相.
氢在过渡金属表面的解离吸附路径问题一直倍受关注.计算模拟需要预先设计氢分子的解离路径,最佳路径通常需满足:最终吸附构型为氢原子的稳定吸附位置以及接近表面路径具有高对称性两个条件.因此,认为氢在过渡金属(100)面的解离吸附路径应为h-b-h.但存在争议,如:氢分子在Pd(100)面上沿h-t-h路径解离吸附,在Rh(100)面上先沿b-t-b路径吸附,然后扩散到四重洞位.
很多学者还计算了氢分子在在Pd(111)、Pd(110)、Rh(111)等金属表面的解离吸附,近年来也有学者对氢在合金中吸附行为进行了研究[23],但对于氢在结构复杂且有缺陷的金属表面上解离吸附问题,尚有很大的研究空间.
2.2.2 氢在金属晶格中的扩散氢在金属中扩散时,晶体结构不同,原子的跳动方式也会不同,因此,扩散机制也不一样.金属中氢原子的扩散机制主要有:间隙扩散、空位扩散和换位扩散3种机制.研究者利用第一性原理计算方法对氢在金属中沿不同路径的扩散激活能进行计算,通过比较激活能的大小得到最佳扩散路径,并进一步计算扩散系数.
Song[24]等人采用密度泛函理论研究了氢在Pd3Ag中的扩散行为,扩散路径为八面体间隙-四面体间隙-八面体间隙,与Pd[25]、Rh[26]扩散路径相同,但扩散激活能大于Pd,可见Ag减弱了氢的扩散能力.魏洪源等[27]研究了氢在Pu中的扩散行为,认为氢原子最可能在相邻的不同间隙位之间进行交替扩散.刘松等人[28]研究了氢在Ti中的扩散行为,研究表明氢原子在α-Ti晶格中沿八面体间隙-四面体间隙-四面体间隙-八面体间隙路径扩散,在β-Ti晶格中沿四面体间隙-四面体间隙路径扩散,在β-Ti的扩散激活能小于α-Ti中,推测在α+β钛合金中,氢主要在β相四面体间隙之间扩散.德国学者Matous[29]等还专门研究了量子力学效应对氢在Fe、Ni中扩散系数的影响,也有学者研究了空位、杂质元素对氢原子扩散行为的影响[30].
综上研究可见,目前针对氢扩散行为的研究主要集中在完美金属晶格基础上,缺少对于存在缺陷的金属晶格中原子扩散行为的研究,这是未来需要解决的问题.
2.3 金属-氢系统的力学性质 2.3.1 氢对金属表面能的影响表面能指表面分子层所具有的势能,由物质内部的分子迁移到表面做的功转化而成.表面能越高,物质稳定性越差.
第一性原理可用于多个领域材料的表面能计算[31-32],有学者[33]计算对比了Ti(0001)、Cu(111)、Al(111)、Mg(0001)的表面能依次为:2.034、1.793、0.864、0.716 eV,与实验相符,说明了第一性原理在表面能计算中的可靠性.2010年,日本学者Udagawa[34]等利用VASP软件计算了不同氢浓度下的hcp-Zr-H和δ-ZrH1.5系统的表面能,模型如图 3所示.表面能计算表达式为

|
图 3 ZrH1.5(111)表面能及层错能计算模型[34] Figure 3 Schematic views of surface energy calculation and γ-surface calculation in the ZrH1.5(111) plane: (a)perfect; (b)unstuck; (c)faulted structures[34] |
| $ 2{\gamma _{\text{s}}} = E_{{\text{tot}}}^{{\text{surf}}} - E_{{\text{tot}}}^{{\text{orig}}}. $ |
式中:Etotsurf为完整结构的上下部分分开后的结构总能量(图 3(b));Etotorig为原始完整结构总能量(图 3(a)).
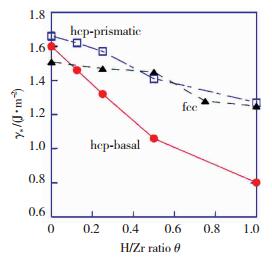
图 4所示为α-Zr—H基面及棱柱面、δ-ZrH1.5{111}面的表面能γs随氢含量的变化.纯Zr基面及棱柱面表面能分别为1.6、1.66 J/m2,与Domain[35]所得相同.氢的加入会降低表面能,且随氢含量增加表面能逐渐降低;当H与Zr的原子数目之比H/Zr(θ) < 0.5时,在α-Zr—H中,表面能降低了15%~34%,基面的表面能小于棱柱面,δ-ZrH1.5表面能降低25%.也有研究[36]表明氢原子使Fe和Al表面能线性降低.由此可见,H的加入提高了金属稳定性.
2.3.2 氢对金属层错能的影响层错使晶体内原子排列出错,对其正常的周期性造成破坏,使晶体能量升高,这种能量即层错能γSF.层错能的高低会影响材料塑性变形的难易程度,位错的滑移和孪生可以通过降低材料的层错能来激发,是优化材料力学性能的一种方法[37].
不稳定堆垛能γus是广义堆垛能的最大值,它会影响到位错芯区的结构,进一步影响材料的韧脆性.材料韧性可以通过表面能γs与不稳定堆垛能γus的比值D=γs/γus来表征.材料韧性与D值大小呈正相关,D值越小,材料越脆.
通过计算错配u=0和u≠0的两个超晶胞总能量之差可以确定广义堆垛能.
| $ {\gamma _{{\text{GSF}}}}\left( u \right) = \frac{{E\left( u \right) - E\left( 0 \right)}}{A}. $ |
式中:A为错配面的面积; E(u)和E(0)(图 3(c)和(a))分别是错配为u和0时的超晶胞总能.
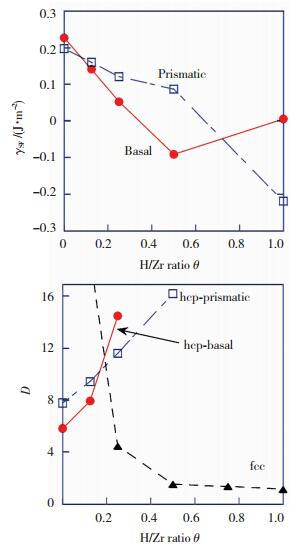
Udagawa等[34]对Zr—H系统第一性原理研究表明,不稳定堆垛能γus与层错能γSF在α-Zr—H基面要比棱柱面大,这与实验结果一致.且随氢含量增加两种能量逐渐降低,如图 5(a)所示.
|
图 5 H含量对层错能(a)及D的影响(b)[34] Figure 5 Influence of H concentration on (a) stacking fault energy and (b) Rice's parameter D[34] |
但当氢与锆的原子数量比达到1时,由于基面上的氢原子会相互排斥,致使层错能急速增大,氢原子排列稀疏的棱柱面上的层错能没有这一突变.图 5(b)为材料韧性指标D随氢含量的变化规律图,可以看到, α-Zr—H的韧性随氢含量增加而变好,但δ-ZrH1.5的韧性却变差.最近,对Zr基面层错能的研究也得到了相同结论[38].国内Wei[39]等人对TiAl-Ti3Al合金的第一性原理的研究也表明氢降低了合金的层错能.
金属-氢系统层错能的计算相对复杂,鲜有学者进行研究,而现有研究的计算体系相对较小且单一,有待进一步研究较复杂体系.
2.3.3 氢对金属弹性模量的影响弹性模量是反映材料性能的重要参数,其值越小,越易发生弹性变形,晶体结构、键和方式、材料成分等都影响到弹性模量的大小.很多学者通过第一性原理计算研究材料的弹性模量,并得到了很有价值的结果[40-41].
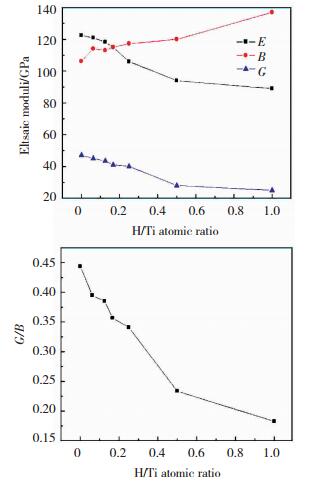
对Ti—H系统应用第一性原理[42]研究其弹性性质,如图 6所示,发现随着氢含量的增加,α-Ti—H晶体的体弹性模量增大,杨氏模量和剪切模量降低,G/B的值随着氢含量的增加而减小,说明氢原子的加入会增加钛的塑性,这与实验结果相符,验证了氢致α-Ti软化的理论.
|
图 6 α-Ti—H体系中氢含量对模量(a)和G/B(b)的影响[42] Figure 6 Influence of H concentration on (a) modulus and (b) G/B of α-Ti—H[42] |
同时,研究也证明氢会使W塑性增强[43].但在β-Ti—H晶体中(图 7),3种模量与氢含量均正相关,造成氢致β-Ti硬化,这与氢提高了其周围Ti—Ti原子间键的强度相符.

|
图 7 β-Ti—H体系模量(a)和G/B(b)随氢含量的变化图[42] Figure 7 Influence of H concentration on (a) modulus and (b) G/B of β-Ti—H[42] |
国内有学者研究了氟化钙结构的不同金属氢化物MH2的弹性模量,见表 4.不同MH2的晶格常数也不同,体弹模量、杨氏模量和剪切模量也不同.且晶格常数越大,弹性模量越小.
推测这种规律产生的原因是由于晶格常数增大会使MH2原子之间产生相互作用的距离变长,平均价键强度减弱,导致MH2抵抗弹性变形的能力减弱,即弹性模量减小.已有研究表明,氢既有可能软化金属也有可能硬化金属,其作用效果不但受到金属种类的影响,还受到晶格结构的影响.但实际工作条件下,金属并不只是在0 K下服役,更高更低的温度都是存在的,而在这些温度下的力学性质更具有现实的指导意义,因此,有必要发展新的计算方法,进行深入研究.
3 讨论计算机模拟技术是目前研究金属-氢之间相互作用比较有效的方法,第一性原理是理论上最严格和最具前途的计算方法,也是最复杂的方法.
本文对目前金属-氢系统性质的研究成果进行了整理分析,阐明了已知的金属-氢之间的相互作用,发现金属种类、晶格类型及常数等都会影响到氢对金属的作用,其根本原因源于不同金属之间电子结构的不同.目前对无缺陷金属-氢系统的基本性质已经有了广泛的研究,未来可以研究带有缺陷(晶界、位错、空位等)的金属-氢系统的性质,如:氢在结构复杂的台阶缺陷金属表面的解离吸附、各种缺陷对氢扩散的影响等,也可研究温度、压强等外界条件的变化对系统影响.
但第一性原理计算也有不可忽视的局限性,计算原子数目有限且速度慢,猜测的一些泛函、参数虽提高了计算速度但确降低了精度.此外,由于氢和金属之间的相互作用相当复杂,一些基本问题尚不清楚,研究空间还很大.但随着计算方法及高性能计算的发展,这些问题会逐渐得到解决,因此,未来在金属-氢系统的研究中,第一性原理计算方法将会发挥更大的作用,对金属-氢系统的认识也会更加深入、全面.
| [1] |
韩秀丽, 王清, 孙东立, 等. 钛-氢体系晶体结构和能量的第一原理计算[J]. 中国有色金属学报, 2008, 18(3): 523–528.
HAN Xiuli, WANG Qing, SUN Dongli, et al. First-principles calculation of crystal structures and energies of Ti-H system[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(3): 523–528. DOI: 10.19476/j.ysxb.1004.0609.2008.03.024 |
| [2] |
张凤春, 李春福, 文平, 等. 金属Fe与间隙H原子相互作用的密度泛函研究[J]. 物理学报, 2014, 64(22): 22701.
ZHANG Fengchun, LI Chunfu, WEN Ping, et al. Density functional theory studies of the Fe and hydrogen[J]. Acta Physica Sinica, 2014, 64(22): 22701. DOI: 10.7498/aps.63.227101 |
| [3] | DOMAIN C, BESSON R, LEGRIS A. Atomic-scale Ab-initio study of the Zr—H system: Ⅰ. Bulk properties[J]. Acta Materialia, 2002, 50: 3513–3526. DOI: 10.1016/S1359-6454(02)00173-8 |
| [4] | 崔仲圻. 金属学与热处理[M]. 版本. 北京: 机械工业出版社, 2007. |
| [5] | ZENG C A, HU J P, OUYANG C Y. Hydrogen solution in tetrahedral or octahedral interstitial sites in Al[J]. Journal of Alloys and Compounds, 2011, 509: 9214–9217. DOI: 10.1016/j.jallcom.2011.06.115 |
| [6] | JIANG D E, CARTER E A. Diffusion of interstitial hydrogen into and through bcc Fe from first principles[J]. Physical Review B, 2004, 70: 064102. DOI: 10.1103/PhysRevB.70.064102 |
| [7] |
陈汝承.钪、钇、饵金属中氢、氦行为的密度泛函理论研究[D].成都: 电子科技大学, 2012. CHEN Rucheng. Density functional theory studies of the H, He in Sc, Y and Er[D].Chengdu: Electronic Science and Technology University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10614-1012472298.htm |
| [8] | KAMAKOTI P, SHOLL D S. A comparison of hydrogen diffusivities in Pd and CuPd alloys using density functional theory[J]. Journal of Membrane Science, 2003, 225: 145–154. DOI: 10.1016/j.memsci.2003.07.008 |
| [9] | ISMER L, PARK M S, JANOTTI A, et al. Interactions between hydrogen impurities and vacancies in Mg and Al: A comparative analysis based on density functional theory[J]. Physical Review, 2009, 80(18): 184110. DOI: 10.1103/PhysRevB.80.184110 |
| [10] | OUYANG C Y, LEE Y S. Hydrogen-induced interactions in vanadium from first-principles calculations[J]. Physical Review B, 2011, 83(4): 045111. DOI: 10.1103/PhysRevB.83.045111 |
| [11] | KONG Xiangshan, WU Xuebang, LIU C S, et al. First-principles calculations of transition metal solute interactions with hydrogen in tungsten[J]. International Atomic Energy Agency, 2016, 56: 026004. DOI: 10.1088/0029-5515/56/2/026004 |
| [12] | YANG Xiaoyong, LU Yong, ZHANG Ping. First-principles study of the stability and diffusion properties of hydrogen in zirconium carbide[J]. Journal of Nuclear Materials, 2016, 479: 130–136. DOI: 10.1016/j.jnucmat.2016.07.008 |
| [13] | SUN Lu, JIN Shuo, ZHOU Hongbo, et al. Dissolution and diffusion of hydrogen in a molybdenum grain boundary: A first-principles investigation[J]. Computational Materials Science, 2015, 102: 243–249. DOI: 10.1016/j.commatsci.2015.02.049 |
| [14] | QIN Shiyao, SHUO Jin, SUN Lu, et al. Hydrogen assisted vacancy formation in tungsten: A first-principles investigation[J]. Journal of Nuclear Materials, 2015, 465: 135–141. DOI: 10.1016/j.jnucmat.2015.05.040 |
| [15] | ZHANG Pengbao, ZHOU Tingting, ZHAO Jijun, et al. Diffusion and retention of hydrogen in vanadium in presence of Ti and Cr: First-principles investigations[J]. Journal of Nuclear Materials, 2017, 484: 276–282. DOI: 10.1016/j.jnucmat.2016.12.013 |
| [16] |
郭宇.氢致Ni-A1系金属间化合物脆性的第一性原理研究[D].哈尔滨: 哈尔滨理工大学, 2015. GUO Yu. First principlies study on hydrogen embrittle of Ni—Al intermetallic compounds[D]. Harbin: Harbin University of Science and Technology, 2015 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D632255 |
| [17] |
韩秀丽.氢在钛晶体中作用的第一原理计算和分子动力学模拟研究[D].哈尔滨: 哈尔滨工业大学, 2010. HAN Xiuli. Research of hydrogen in Ti by first principles calculation and molecular dynamics simulation[D]. Harbin: Harbin Institute of Technology, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D269281 |
| [18] |
饶建平, 欧阳楚英, 雷敏生, 等. 第一性原理计算研究金属Nb和间隙氢原子的相互作用[J]. 物理学报, 2012, 4: 047105.
RAO Jianping, OUYANG Chuying, LEI Minsheng, et al. First principles investigation of interaction between interstitials H atom and Nb metal[J]. Acta Phys Sin, 2012, 4: 047105. DOI: 10.7498/aps.61.047105 |
| [19] | LOPATINA O V, SVYATKIN L A, KOROTEEV Y M, et al. Electronic structures of the Zr-He, Zr-H, and Zr-He-H systems[J]. Physics of the Solid State, 2015, 57(9): 1679–1684. DOI: 10.1134/S106378341509022X |
| [20] |
石瑜, 白洋, 莫丽玢, 等. H掺杂α-Fe2O3的第一性原理研究[J]. 物理学报, 2015, 64(11): 116301.
SHI Yu, BAI Yang, MO Lifen, et al. First-principles calculation for hydrogen-doped hematite[J]. Acta Physica Sinica, 2015, 64(11): 116301. DOI: 10.7498/aps.64.116301 |
| [21] | HUO Chunfang, LI Yongwang, WANG Jianguo, et al. Surface structure energetics of hydrogen adsorption on the Fe(111) surface[J]. Journal of Physical Chemistry B, 2005, 109(29): 14160–14167. DOI: 10.1021/jp051907s |
| [22] | SHEN Xiangjian, CHEN Jun, SUN Y M, et al. Hydrogen diffusion on Fe surface and into subsurface from first principles[J]. Surface Science, 2016, 654: 48–55. DOI: 10.1016/j.susc.2016.08.005 |
| [23] | DAI J, JIANG X, SONG Y. First-principles investigations of transition metal dihydrides[J]. Surface Science, 2016, 653: 22–26. DOI: 10.1088/0953-8984/12/21/301 |
| [24] | WANG J W, SONG M, HE Y H, et al. Stability, adsorption, and diffusion of hydrogen in Pd3Ag phases[J]. Journal of Membrane Science, 2016, 503: 124–131. DOI: 10.1016/j.memsci.2015.11.021 |
| [25] | SARANTOKH Nasantogtokh, CUI Xin, WANG Zhiping. First-principles study of hydrogen diffusion in transition metal palladium[J]. Modern Physics Letters B, 2015, 29(13): 012047. DOI: 10.1142/S0217984915500645 |
| [26] |
乌力吉毕力格.过渡金属铑中氢扩散的第一性原理研究[D].内蒙古: 内蒙古大学, 2014. WULIJI Bilige. First principles study of hydrogen diffusion behavior in Rh[D]. Inner Mongolia: Inner-Mongolian University, 2014 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2729428 |
| [27] |
魏洪源, 罗顺忠, 刘国平, 等. H原子在完美δ-Pu金属体相中的扩散行为[J]. 物理化学学报, 2008, 24(11): 1964–1968.
WEI Hongyuan, LUO Shunzhong, Liu Guoping, et al. Hydrogen diffusion behavior in perfect δ-Pu metal[J]. Acta Physico-Chimica Sinica, 2008, 24(11): 1964–1968. DOI: 10.3866/PKU.WHXB20081105 |
| [28] |
刘松, 王寅岗. 氢在钛晶体中扩散行为的第一性原理[J]. 中国有色金属学报, 2015, 25(11): 3100–3106.
LIU Song, WANG Yangang. First-principles of hydrogen diffusion mechanism in titanium crystals[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(11): 3100–3106. DOI: 10.19476/j.ysxb.1004.0609.2015.11.018 |
| [29] | STEFANO D D, MROVEC M, ELSASSER C. First-principles investigation of quantum mechanical effects on the diffusion of hydrogen[J]. Physical Review B, 2015, 92: 224301. DOI: 10.1103/PhysRevB.92.224301 |
| [30] | XIN Jinghua, WANG Jianchuan, DU Yong, et al. Site preference and diffusion of hydrogen during hydrogenation of Mg: A first-principles study[J]. Science Direct, 2016, 41: 3508–3516. DOI: 10.1016/j.ijhydene.2015.12.157 |
| [31] | YAN Wenli, SYGNATOWICA, LU Guanghong, et al. First-principles study on surface stability of tantalum carbides[J]. Surface Science, 2016, 644: 24–28. DOI: 10.1016/j.susc.2015.09.003 |
| [32] | XU Bin, CHEN Leiming. First-principles study on half-metallic zinc-blende CrS and its (001) surface[J]. Journal of Magnetism and Magnetic Materials, 2016, 417: 21–24. DOI: 10.1016/j.jmmm.2016.05.027 |
| [33] | LIU Yu, HUANG Yuanchun, XIAO Zhengbing, et al. Study of adsorption of hydrogen on Al, Cu, Mg, Ti surfaces in al alloy melt via first principles calculation[J]. Metals, 2017, 7(1): 21. DOI: 10.3390/met7010021 |
| [34] | UADGAWA Y, YAMAGUCHI M, ABE H, et al. Ab initio study on plane defects in zirconium-hydrogen solid solution and zirconium hydride[J]. Acta Materialia, 2010, 58(11): 3927–3938. DOI: 10.1080/00223131.2012.676820 |
| [35] | DOMAIN C, BESSON R, LEGRIS A. Atomic-scale Ab-initio study of the Zr—H system: Ⅱ. Interaction of H with plane defects and mechanical properties[J]. Acta Materialia, 2004, 52: 1495–1502. DOI: 10.1016/j.actamat.2003.11.031 |
| [36] | JIANG D E, CARTER E A. First principles assessment of ideal fracture energies of materials with mobile impurities: Implications for hydrogen embrittlement of metals[J]. Acta Materialia, 2004, 52: 4801–4807. DOI: 10.1016/j.actamat.2004.06.037 |
| [37] | ZHAO Y H, ZHU Y T, LIAO X Z, et al. Tailoring stacking fault energy for high ductility and high strength in ultrafine grained Cu and its alloy[J]. Applied Physics Letters, 2006, 89(12): 121906. DOI: 10.1063/1.2356310 |
| [38] | HOU Songjun, LEI Huaping, ZENG Zhi. Hydrogen influence on generalized stacking fault energies of Zr {0001} basal plane: A first-principles study[J]. RSC Advances, 2016, 6(59): 54371–54376. DOI: 10.1039/C6RA10683H |
| [39] | WEI Y, ZHANG Y, LU G H, et al. A first-principles study of site occupancy and interfacial energetics of an H-doped TiAI-Ti3A1 alloy[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(2): 228–234. DOI: 10.1007/s11433-011-4600-x |
| [40] | SHEN Tao, FENG Yue, HU Chao. First-principles calculations of structural and mechanical properties of YFeO3[J]. Optoelectronics and Advanced Materials-Rapid Communications, 2016, 10(3-4): 268–272. |
| [41] | HU Hai, WU Xiaozhi, WANG Rui, et al. Structural stability, mechanical properties and stacking fault energies of TiAl3 alloyed with Zn, Cu, Ag: First-principles study[J]. Journal of Alloys and Compounds, 2016, 666: 185–196. DOI: 10.1016/j.jallcom.2016.01.106 |
| [42] |
杨诚.氢致纯钛弹塑性变形机制研究[D].哈尔滨: 哈尔滨工业大学, 2015. YANG Cheng. Research of eleastic-plastic deformation mechanism in Ti—H system[D]. Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015981048.htm |
| [43] |
张铮, 赵强, 欧阳晓平. 氢氦在钨中的影响的第一性原理研究[J]. 核化学与放射化学, 2016, 38(1): 19–24.
ZHANG Zheng, ZHAO Qiang, OUYANG Xiaoping. First-principles study on effect of hydrogen and helium in tungsten[J]. Journal of Nuclear and Radiochemistry, 2016, 38(1): 19–24. DOI: 10.7538/hhx.2016.38.01.0019 |
| [44] |
代云雅, 杨莉, 彭述明, 等. 金属氢化物力学性能的第一性原理研究[J]. 物理学报, 2012, 61(10): 108801.
DAI Yunya, YANG Li, PENG Shuming, et al. First-principles calculation for mechanical properties of metal dihydrides[J]. Acta Physica Sinica, 2012, 61(10): 108801. DOI: 10.7498/aps.61.108801 |
| [45] | TAO S X, NOTTEN P H L, SANTEN Van R A, et al. Fluorite transition metal hydride induced destabilization of the MgH2 system in MgH2/TMH2 multilayers (TM=Sc, Ti, V, Cr, Y, Zr, Nb, La, Hf)[J]. Physical Review B, 2010, 82(12): 125448. DOI: 10.1103/PhysRevB.82.125448 |
| [46] | WOLF W, HERZIG P. First-principles investigations of transition metal dihydrides, TH2: T = Sc, Ti, V, Y, Zr, Nb; energetics and chemical bonding[J]. Journal of Physics-Condensed Matter, 2000, 12(21): 4535–4551. DOI: 10.1088/0953-8984/12/21/301 |
 2018, Vol. 26
2018, Vol. 26