2. 南昌大学 材料科学与工程学院,南昌 330031
2. College of Materials Science and Engineering, Nanchang University, Nanchang 330031, China
纤维铺层复合结构由于其高强度、低密度、设计灵活多变等特点,已被广泛应用于生活的各个领域.尤其是碳纤维的铺层复合结构,其具备模量高(平均为钢的10倍)、密度低等优点,已经在军用设备、国防装备、航空航天及高端民用领域得以普遍使用.当前,在高强材料研究领域,碳纤维复合材料研究较普遍[1-5].例如,袁威等[1]研究了5种不同铺层方式的碳纤维环氧树脂材料复合矩形截面的抗弯性能;韩斌斌等[2]采用Ansys ACP数值手段对碳纤维复合综框结构进行了铺层优化设计;史红彬等[3]采用LS-DYNA程序,对碳纤维/环氧树脂复合圆筒材料进行低速冲击损伤的评估[4].本文则关注碳纤维铺层结构在高端民用体育器材类的应用领域.通常木质滑板结构的承载极限在300~400 kg,而相同尺寸的碳纤维/环氧复合铺层滑板结构的压载能力可达数吨以上.这大大提高了滑板器材的使用安全系数和可靠性能.
本文通过一种常用且独特的设计铺层方式,以热固性环氧树脂为基体材料,直纹编织碳纤维布和交叉编织的玻璃纤维布为增强材料,并采用实验和复合结构的数值分析手段,采用Cuntze失效准则[5-7],研究复合滑板压弯过程中滑板结构基体失效导致的层离失效及纤维失效.
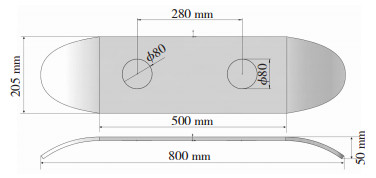
1 实验 1.1 滑板复合结构的总体尺寸及铺层复合方式本文设计和研究的纤维铺层复合滑板结构尺寸如图 1所示.它分为3部分:2个曲边结构及1个平板结构,这3类结构都采用一体化手工糊边制备,每一层铺层都由单层连续纤维布组成.滑板的整体长度为800 mm,整体宽度为205 mm,总体厚度约为13 mm.由于结构内部分布了4层加强层(见图 2),以及铺层过程中树脂的涂抹厚度局部不均匀,总体厚度也会产生相应的偏差.其中,平板结构的长度为500 mm,单边曲边部分长度为150 mm,曲边卷曲高50 mm.同时,由于直板及脚踏部位是作用力集中区域,因此在该部位增加了4层内强化层(具体铺层细节参见图 2).其中,2层为双圆形强化层,圆形直径80 mm,另外2层为矩形强化层,其长和宽分别为500、205 mm.
|
图 1 滑板结构的铺层设计尺寸 Fig.1 Dimension of layers in sikds |
|
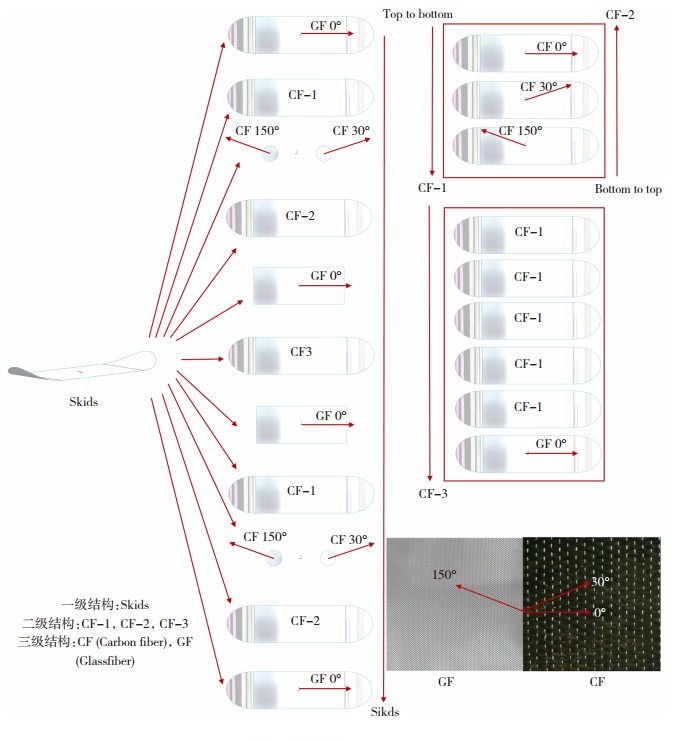
图 2 滑板结构的铺层方式 Fig.2 Layers of skids structure |
本文采用的滑板结构铺层方式如图 2所示,复合滑板的实物与有限元模型见图 3.

|
图 3 复合滑板的实物与有限元模型 Fig.3 Real object and FEM of composite skids: (a) real object of composite skids; (b) FEM of composite skids; (c) thickness distribution of composite skids |
总体采用碳纤维增强材料,只在滑板上下表面各增设一层玻璃纤维起到降低表面硬度、增大表面摩擦系数的作用.其中,单层玻璃纤维布为双向正交编织结构,厚度为0.2 mm;而碳纤维为单向编织结构,厚度为0.4 mm.整个滑板的铺层结构都是呈中心对称式铺层.它又分为2个三级结构(单层碳纤维铺层结构和单层玻璃纤维铺层结构)和3个二级铺层结构(CF-1、CF-2、CF-3).总铺层数为34层,理论铺层总厚度为13.2 mm(0.4 mm×32+0.2 mm×2).在铺层设计中,既要考虑纤维材料在0°方向的力学强度,又要兼顾部分90°方向的力学强度.通常来说,复合板宽度/复合板长度=(正向或反向)设计铺层角/90°.
但是,考虑到制备过程的边角料浪费和成本问题,本文将整个滑板结构的铺层角度总体分为3个方向,分别是0°、30°和150°.其中,碳纤维和玻璃纤维的0°铺层方向为平行于纤维排布的应力主方向,如图 2右下角所示.本文中碳纤维的孔隙率为2.7%,玻璃纤维的孔隙率为0.6%.
1.2 铺层结构的力学性能整个滑板结构采用2种纤维布和1种树脂基所组成,因此,使用数值分析时需要同时考虑到这3种材料对整体结构力学特点的贡献及其对应的不同失效机理.综合考虑铺层结构的基体失效、层离失效及纤维失效的问题,需要确定3种材料在不同方向上的弹塑性及失效的本构特点.由于环氧树脂基体为各项同性,而纤维材料在不同方向上的失效特点为各向异性,因此,纤维材料的应力应变极限属性需要在3个坐标方向上分开确定.具体材料数据参数如表 1~3所示.
| 表 1 碳纤维的力学特性 Table 1 Mechanical properties of carbon fibre |
| 表 2 玻璃纤维的力学特性 Table 2 Mechanical properties of glass fibre |
| 表 3 热固性环氧树脂(固化后)的力学特性 Table 3 Mechanical properties of thermosetting epoxy resin (after curing) |
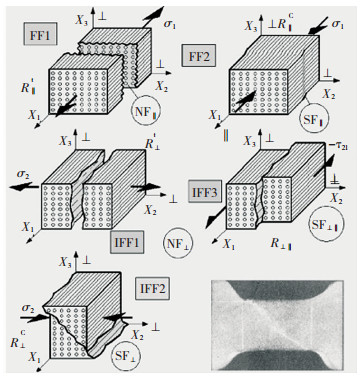
本文采用Cuntze失效准则[6-7]来判定复合滑板在受压状态下的层间失效及损伤.纤维复合材料的Cuntze的失效判定方法是基于它的不变量表述的失效模型概念(可用于各向同性和各向异性材料),在这里运用到横向的各向同性碳纤维UD(单向织物,Uni-Directional Fabric, 后文简称UD材料)材料中.这个概念严格地将5种强度失效模式固有地分配到了UD材料中.由于材料的对称性,需要在5个方向上测量相应的强度,同时,损伤实验的物理的断口形貌指明了每种失效模式仅仅只受一个单一方向上的强度支配(图 4).
|
图 4 UD失效模型 Fig.4 UD failure model |
Cuntze的强度失效条件Strength failure condition(SFC)[6]也可以称为模态条件,它依赖于在一种失效模式下的失效函数(F),而且只包含在这一种相关强度模式中:
| $ {F^{{\rm{mode}}}}\left( {\left\{ \sigma \right\},\left\{ {{R^{{\rm{mode}}}}} \right\}} \right) = 1. $ | (1) |
式中:{σ}为应力张量,包含了6个应力矢量{σ}=(σ1, σ2, σ3, σ23, σ31, σ21)T;Rmode为一种强度模式.
一组模态SFCs需要考虑5种失效模式的相互作用.所观察到的失效模式包括2种纤维失效模式(FF1拉伸和FF2压缩)和3种纤维间失效模式(IFF1横向拉伸、IFF2横向压缩和IFF3剪切).它们这5类模式总体包含了纤维基体之间的内聚力和粘聚力矩阵的失效形式.
Cuntze也提供了5类脆性UD材料失效模式的等效应力,它类似于Hencky-Mises-Huber延展性材料的屈服失效模型[7].
一个等效应力(σeq)包括在一个给定失效模式下的所有应力作用在一起的效果.包含所有等效应力的矢量为
| $ \left\{ {\sigma _{{\rm{eq}}}^{{\rm{mode}}}} \right\} = {\left( {\sigma _{{\rm{eq}}}^{\parallel \sigma },\sigma _{{\rm{eq}}}^{\parallel \tau },\sigma _{{\rm{eq}}}^{ \bot \sigma },\sigma _{{\rm{eq}}}^{ \bot \tau },\sigma _{{\rm{eq}}}^{\parallel \bot }} \right)^{\rm{T}}}. $ | (2) |
式中:{σeqmode}为等效应力张量的失效模式;σeqσ、σeqτ、σeq⊥σ、σeq⊥τ和σeq⊥分别为5种等效应力矢量失效模式,它们的矢量方向分别对应于图 4中的FF1、IFF1、IFF2、FF2和IFF3.
这里的等效应力、模式强度和材料应力效应material stressing effort(EFF)的关系为:
| $ E_{ff}^{{\rm{mode}}} = \frac{{\sigma _{{\rm{eq}}}^{{\rm{mode}}}}}{{{{\bar R}^{{\rm{mode}}}}}}, $ | (3) |
| $ {X_{\rm{t}}} = R_\parallel ^{\rm{t}};{X_{\rm{c}}} = R_\parallel ^V;{Y_{\rm{t}}} = R_ \bot ^{\rm{t}};{Y_{\rm{c}}} = R_ \bot ^{\rm{c}};{S_{xy}} = {R_{ \bot \parallel }}. $ | (4) |
式中:Effmode为材料的应力效应;Rmode为平均模式强度;X表示X方向的失效强度;Y表示Y方向的失效强度;S表示剪切失效强度;R为模式强度;角标‖表示平行方向,⊥为垂直方向,‖⊥为剪切方向,c表示压缩,t表示拉伸.
这里字母上面的横杠标记了静态的平均值,并且模式强度可以被各自的材料应力极限所替代.除了5个强度之外,Cuntze采用2个材料固有失效参数b⊥‖和bb⊥⊥(由Mohr-Coulomb提出),因为SFCs对于脆性材料不能基于单一的强度值.宏观力学SFCs必须考虑到,对于纤维失效模式来说,材料失效可能会在宏观水平起作用.
5种用于形成5类SFCs(2D 3D)[5]的不变量为:
| $ \begin{array}{l} {I_1} = {\sigma _1},\\ {I_2} = {\sigma _2} + {\sigma _3},\\ {I_3} = \tau _{31}^2 + \tau _{21}^2,\\ {I_4} = {\left( {{\sigma _2} - {\sigma _3}} \right)^2} + 4 \cdot \tau _{23}^2,\\ {I_5} = {\left( {{\sigma _2} - {\sigma _3}} \right)^2} \cdot \left( {\tau _{31}^2 - \tau _{21}^2} \right) - 4 \cdot {\tau _{23}} \cdot {\tau _{31}} \cdot {\tau _{21}}. \end{array} $ | (5) |
式中:I1、I2、I3、I4、I5为5种模式失效强度的应力不变量表达式.
对于三维失效问题,替代Cuntze不变量构想的模式失效条件不变量SFCs[7-8]需要伴随相关的应力状态(因素IFF3中不是完全的应力状态组成,但是它是模式失效的驱动应力)并且可以分解为简单的材料应力效应EFF屈服,如下所示:
| $ \begin{array}{l} {\rm{FF1:Ef}}{{\rm{f}}^{\parallel \sigma }} = \frac{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \sigma } }_1}}}{{\bar R_\parallel ^{\rm{t}}}} = \frac{{\sigma _{{\rm{eq}}}^{\parallel \sigma }}}{{\bar R_\parallel ^{\rm{t}}}},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \sigma } }_1} \cong \varepsilon _1^{\rm{t}} \cdot {E_\parallel }.\\ {\rm{FF2:Ef}}{{\rm{f}}^{\parallel \tau }} = \frac{{ - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \sigma } }_1}}}{{\bar R_\parallel ^{\rm{c}}}} = \frac{{\sigma _{{\rm{eq}}}^{\parallel \tau }}}{{\bar R_\parallel ^{\rm{c}}}},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \sigma } }_1} \cong \varepsilon _1^{\rm{c}} \cdot {E_\parallel }.\\ {\rm{IFF1:Ef}}{{\rm{f}}^{ \bot \sigma }} = \frac{{\left( {{\sigma _2} + {\sigma _3}} \right) + \sqrt {{{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + 4\tau _{23}^2} }}{{2\bar R_ \bot ^4}} = \frac{{\sigma _{{\rm{eq}}}^{ \bot \sigma }}}{{\bar R_ \bot ^{\rm{t}}}}.\\ {\rm{IFF2:Ef}}{{\rm{f}}^{ \bot \tau }} = \\ \;\;\;\;\;\frac{{\left( {b{b_{ \bot \bot }} - 1} \right)\left( {{\sigma _2} + {\sigma _3}} \right) + b{b_{ \bot \bot }}\sqrt {{{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + 4\tau _{23}^2} }}{{\bar R_ \bot ^{\rm{c}}}} = \\ \;\;\;\;\;\frac{{\sigma _{{\rm{eq}}}^{ \bot \sigma }}}{{\bar R_ \bot ^{\rm{c}}}}.\\ {\rm{IFF3:Ef}}{{\rm{f}}^{ \bot \parallel }} = \\ \;\;\;\;{\left( {\frac{{{b_{ \bot \parallel }}{I_{23 - 5}} + \sqrt {b_{ \bot \parallel }^2{I_{23 - 5}} + 4R_{ \bot \parallel }^2{{\left( {\tau _{31}^2 + \tau _{21}^2} \right)}^2}} }}{{2\bar R_{ \bot \parallel }^3}}} \right)^{0.5}} = \frac{{\sigma _{{\rm{eq}}}^{ \bot \parallel }}}{{{{\bar R}_{ \bot \parallel }}}}. \end{array} $ | (6) |
其中, I23-5=2σ2τ212+2σ3τ212+4τ23τ31τ21.式中:Eff为材料应力效应的屈服强度;I23-5为一组应力组合方式;ε为应变;E为弹性模量;b为摩擦参数;上下标表示其矢量方向,如前文所述.
摩擦参数(b)可以通过可用的UD材料摩擦系数计算,如文献[8]所述:
| $ \begin{array}{l} {b_{ \bot \parallel }} \cong 2 \cdot {\mu _{ \bot \parallel }},\\ b{b_{ \bot \bot }} \cong \frac{1}{{\left( {1 - {\mu _{ \bot \bot }}} \right)}}. \end{array} $ | (7) |
式中,μ为摩擦系数,数值范围为
| $ 0.5 < {\mu _{ \bot \parallel }} < 0.3,\;\;\;\;0.5 < {\mu _{ \bot \bot }} < 0.2. $ |
如果失效角度的测试数据被给定,那么摩擦系数(μ⊥⊥)由式(8)给出[9-12]:
| $ {\mu _{ \bot \bot }} = - \cos \left( {2 \cdot \theta _{fp}^{C \circ } \cdot \frac{{\rm{ \mathsf{ π} }}}{{{{180}^ \circ }}}} \right). $ | (8) |
式中:θfpCº为失效角度(角度制).
或者直接相关的参数(bb⊥⊥)为
| $ b{b_{ \bot \bot }} = \frac{1}{{\left( {1 + C_{fp}^C} \right)}}. $ | (9) |
这里,
| $ C_{fp}^C = \cos \left( {\frac{{2\theta _{fp}^C}}{{180}}{\rm{ \mathsf{ π} }}} \right). $ |
如果IFF2和IFF3曲线是基于足够的测试数据描绘的,那么2个摩擦参数可以采用式(10)构想来确定:
| $ \begin{array}{*{20}{c}} {b{b_{ \bot \parallel }} = \frac{{R_{ \bot \parallel }^4 - \tau _{21,fr}^4}}{{2 \cdot {R_{ \bot \parallel }} \cdot {\sigma _{2fr}} \cdot \tau _{21,fr}^2}},}\\ {{b_{ \bot \bot }} = \frac{{{\sigma _{2, \bot fr}} + {\sigma _{3, \bot fr}} + R_ \bot ^C}}{{{\sigma _{2, \bot fr}} + {\sigma _{3, \bot fr}} + \sqrt {{{\left( { - {\sigma _{2, \bot fr}} + {\sigma _{3, \bot fr}}} \right)}^2}} }}.} \end{array} $ | (10) |
一种相互作用的失效模式产生取决于这个事实,即完全失效面由5部分组成.Cuntze建立的这些相互作用模式是通过一种简单的、基于概率的串联弹簧模型[5].这些模型描述了层状失效系统是一类当体系内任意一个单元失效,则发生体系失效的模式.每一种模式是这种失效系统的一个单元和与其他单元之间相独立的形式.通过这种方法,FF和IFF之间的相互作用形式,以及各类IFF之间的相互作用形式,是一个四舍五入的过程,这种方法能够确定最终的Eff或反阈值系数(IRF).
| $ \begin{array}{l} {\rm{IR}}{{\rm{F}}^m} = E_{ff}^m = {\left( {{\rm{Ef}}{{\rm{f}}^{\parallel \sigma }}} \right)^m} + {\left( {{\rm{Ef}}{{\rm{f}}^{\parallel \tau }}} \right)^m} + \\ \;\;\;\;\;\;\;\;\;\;\;{\left( {{\rm{Ef}}{{\rm{f}}^{\parallel \sigma }}} \right)^m} + {\left( {{\rm{Ef}}{{\rm{f}}^{\bot \tau }}} \right)^m} + {\left( {{\rm{Ef}}{{\rm{f}}^{\bot \parallel }}} \right)^m}. \end{array} $ | (11) |
换言之,相互作用方程包括所有模式的应力效应以及它们之间的每一种都代表了一个材料承载能力的一部分.在2D问题中,5种模式中的最多3种将互相影响.
模式相互作用的指数(m)由相互作用区域内的测试数据的曲线拟合获得.实验数据表明(对于碳纤维复合材料CFRP),通常,2.5 < m < 3.
指数m在低散度下很高,而在高散度下很低,因此,选择一个低的相互作用指数是非常保守的.作为一个工程假设,m通常总是给定一个同样的值,而忽略相互作用域的清晰模式.对于前期设计,Cuntze推荐的值为m=2.6,并且μ=0.1.
2 结果与讨论 2.1 压弯实验压弯实验采用的设备是三思微机控制电子万能试验机,型号为CMT5205,最大试验力为200 kN,输出功率为3 kW.复合滑板结构由2个枕木垫起,枕木尺寸为300 mm×100 mm,2块枕木间距为300 mm.如图 5所示.其中,图 5(a)所示的为压载试验前工况,图 5(b)为加载后的滑板,图 5(c)为加载后形成的层离失效面,图 5(d)为加载后形成的基体失效印记.

|
图 5 复合滑板结构的压载试验及失效情况 Fig.5 Ballast est and failure of composite skids: (a) experiment layout of ballast; (b) structure of skids after experiment; (c) strip surface of loading procedure; (d) local failure condition of skids after loading |
根据图 5所示,压弯实验中碳纤维复合滑板形成了比较明显的层离失效和基体失效情况,但是表面层纤维失效并不明显(内部层的纤维失效无法直接观察,但通过数值分析结果可以获取到内部的纤维失效信息).
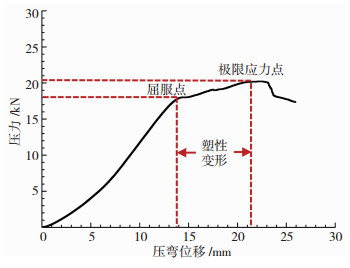
图 6所示为复合滑板结构压载试验过程的压力-位移曲线,根据曲线可知,该复合滑板结构能够承受极限压力载荷(20 220 N)略大于2 t,所对应的压弯位移为21.7 mm.在1.8 t左右时开始产生塑性变形,所对应的压弯位移为13.9 mm.
|
图 6 复合滑板的压弯力-位移曲线 Fig.6 Pressure-displacement curve of composite skids |
采用纤维铺层结构数值分析软件ANSYS Composite Prepost(ACP)对前面所述的压弯实验进行数值模拟,可以方便地定义复合板的铺层及具有丰富的复合材料失效本构,从而对纤维复合结构的受力状况、失效模式进行分析.
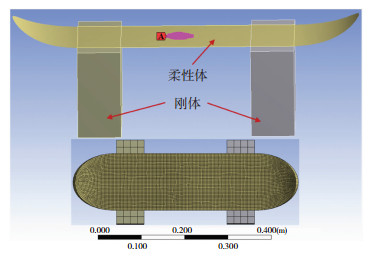
数值模拟采用ACP模块,在这个模块中分为ACP(Pre)和ACP(Post)两部分[13].前者用于定义材料的属性、载荷及便捷条件等前处理信息,后者则专门用于查询复合材料的计算结果及后处理.由于需要对复合板试样进行铺层设置,因此复合板需要采用壳单元来定义,如图 7所示.
|
图 7 有限元模型边界条件及网格的划分 Fig.7 Boundary conditions and meshing of FEM |
复合滑板结构的数值模型中建立了2个实体枕木模型,设定与实验相同的载荷边界条件.由于不考虑枕木的力学性能,只考虑它对复合板的接触边界条件,因此将其设置为刚体,而复合滑板设置为柔性体.同时,模拟中所对应的约束条件为对2个垫片进行全局自由度约束,并且在复合滑板中心A区域施加一个渐进的20 220 N向下的压力.
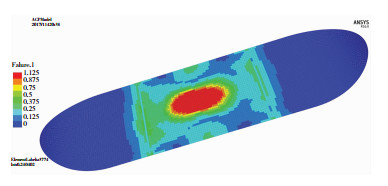
图 8所示是根据数值模拟获取到的复合滑板压弯实验的单元失效分布,但它只反映了全局的失效单元分布特点,以及不同区域单元损伤的严重程度,不能反映每一个失效单元的失效形式及所在的失效层细节.但是根据Cuntze失效准则,需要确定单元的失效类型及所在失效层的计算,需要定义5类失效形式的权重系数.根据前文所述,Cuntze失效可考虑5种失效模态条件,因此它们对应于5种失效形式,包括纤维拉伸失效FF1(代号cft)、纤维压缩失效FF2 (代号cfc)、基体拉伸失效IFF1(代号cmA)、基体压缩失效IFF2(代号cmB)和基体剪切失效IFF3(代号cmC).同时,根据Cuntze建议的UD碳纤维复合材料来说,这5种失效形式所对应的权重系数分别取值为1.0、1.0、1.5、1.7和1.2.
|
图 8 复合滑板单元失效分布 Fig.8 Distribution of element failure in composite skids |
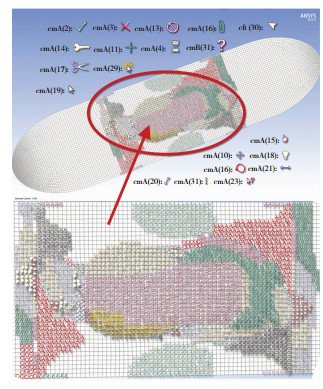
通过对Cuntze失效进行有限元分析,获取复合滑板结构的失效单元失效类型及所在失效层分布的细节,如图 9所示.
|
图 9 失效单元的失效形式及失效层分布 Fig.9 Failure mode and failure layer distribution of failure element |
根据分析结果显示,在加载过程中共20层发生了失效,主要以cmA失效为主(后面括号内的数字表示失效所在的层).同时,在压头周边附近一个椭圆形区域内存在大量的基体压缩失效cmB区域(31)以及部分纤维拉伸失效cft(30)区域.从表观失效特点上看,数值模拟结果与实验结果相符.
3 结论1) 基于UD材料的Cuntze失效准则对碳/玻纤维滑板结构进行压弯性能分析,并对其实验测定,结果表明,该复合结构所能承受高达2 t的质量,远高于普通木质结构,其失效形式主要以基体失效为主,而纤维失效及其微弱,通过数值分析表明,它仅集中于压头加载区域周边的第30层cft(30),该层处于整个滑板最底部的二级结构,且所受加载压力最大.
2) 实验分析与数值模拟结果对比表明,由于滑板在压弯过程中碳纤维上层面与下层面之间存在相互的挤压、滑动等的作用,会形成相应的翘曲变形,而曲率最大则集中于滑板底部,因此,在整个压弯过程中纤维材料的破坏会首先在翘曲变形最大的区域发生.
3) 由于纤维材料与基体材料强度的巨大差异,整个加载过程以环氧树脂基体失效为主(基体失效导致纤维层之间的剥离),纤维失效则非常微弱.因此,整个复合滑板结构的抗压强度主要取决于基体材料的强度,所以,要进一步优化提升滑板的承重能力,可优先选择强度更高的树脂基体,然后再考虑优化纤维的铺层等方式.
| [1] |
袁威, 胡业发, 张锦光. 碳纤维复合材料矩形截面管抗弯性能研究[J]. 玻璃钢/复合材料, 2017(2): 64-68. YUAN Wei, HU Yefa, ZHANG Jinguang. Research on the bending capability of composite fiber reinforced plastic tube with rectangular cross section[J]. FRP/CM, 2017(2): 64-68. DOI:10.3969/j.issn.1003-0999.2017.02.012 |
| [2] |
韩斌斌, 王益轩, 任双宁. 基于ANSYS Workbench碳纤维复合材综框的铺层分析与优化设计[J]. 纺织器材, 2017, 44(3): 140-146. HAN Binbin, WANG Yixuan, REN Shuangning. The ANSYS worckbench layer analysis and optimization design of the heald frame of carbon fiber composite[J]. Tectile Accessories, 2017, 44(3): 140-146. |
| [3] |
史红彬, 杨世源, 王军霞, 等. 碳纤维/环氧树脂复合材料圆筒在低速横向冲击下的数值研究[J]. 材料导报, 2011, 25(12): 148-152. SHI Hongbin, YANG Shiyuan, WANG Junxia, et al. Numerical study of carbn fiber reinforced epoxy composite cylinders subjected to low-velocity transverse impact[J]. Material Review, 2011, 25(12): 148-152. |
| [4] |
肖志, 杜庆勇, 莫富灏, 等. 连续碳纤维增强复合材料汽车顶盖铺层优化[J]. 汽车工程, 2017, 39(6): 722-728. XIAO Zhi, DU Qingyong, MO Fuhao, et al. Ply optimization on ehicle roof of continuous carbon Fiber reinforced Polymer[J]. Automotive Engineering, 2017, 39(6): 722-728. DOI:10.19562/j.chinasae.qcgc.2017.06.018 |
| [5] |
CUNTZE R G, FREUND A. The predictive capability of failure mode concept-based strength criteria for multidirectional laminates[J]. Composites Science and Technology, 2004, 64(3): 343-377. |
| [6] |
CUNTZE R G. Efficient 3D and 2D failure conditions for UD laminae and their application within the verification of the laminate design[J]. Composites Science and Technology, 2006, 66(7/8): 1081-1096. |
| [7] |
CUNTZE R. The predictive capability of failure mode concept-based strength conditions for laminates composed of UD laminas under static tri-axial stress states[J]. Journal of Composite Materials, 2012, 46(19/20): 2563-2594. |
| [8] |
CUNTZE R. Basis Document, Update ComPoLyX Manual Chapter Cuntze and Relationship of Cuntze′s UD Friction Parameters b with Mohr′s Friction Coefficients[M]. Austin: University of Texas Press, 2015: 146-150.
|
| [9] |
PUCK A, SCHNEIDER W. On failure mechanisms and failure criteria of filament-wound glass-fiber/resin composites[J]. Plastic and Polymer Technology, 1969(12): 33-43. |
| [10] |
PUCK A. Festigkeitsberechnung an Glasfaser/Kunststoff-Laminaten bei zusammengesetzter Beanspruchung[J]. Kunststoffe, 1969, 59(11): 780-787. |
| [11] |
PUCK A. Festigkeits analyse von Faser-Matrix-Laminaten Modelle Fur die Praxis[M].[s.l.]: Verlages in Fotokopie, Mikrofilm order ein anderes Verfahren, 1996: 123-131. http://www.doc88.com/p-6953503938348.html.
|
| [12] |
PUCK A, SCHURMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models[J]. Comp Sci Technol, 1998, 58: 1045-1067. DOI:10.1016/S0266-3538(96)00140-6 |
| [13] |
刘笑天, 蒋超奇, 付远, 等. ANSYS Workbench有限元分析工程实例讲解[M]. 北京: 中国铁道出版社, 2017: 270-286.
|
 2019, Vol. 27
2019, Vol. 27


