2. 中国科学院材料力学行为和设计重点实验室(中国科学技术大学),合肥 230026
2. CAS Key Laboratory of Mechanical Behavior and Design of Materials (University of Science and Technology of China), Hefei 230026, China
压延是熔融材料通过压延设备延展成具有一定规格、形状制品的工艺过程.在橡胶行业中,很多半成品都是通过压延得到,如轮胎内衬层、带束层等.早在1950年,Gaskell[1]对牛顿流体和宾汉流体的压延过程进行了理论分析.在此基础上,Kelvey[2]、Chong[3]、Alston等[4]和Brazinsky等[5]运用润滑近似理论对控制方程进行简化,并对幂律流体的压延流场进行了推导,文献[6-8]对这些成果进行了总结.对橡胶这类流变行为较复杂的非牛顿流体而言,上述简化理论模型很难得到符合实际情况的结果.随着计算机技术的发展,许多研究者借助数值模拟手段研究压延问题.Mitsoulis[9]在压延模型中引入了自由表面,通过模拟得到了宾汉流体入口和出口处自由表面的形状.基于有限元软件Polyflow[10],Luther等[11-12]对三维压延过程的速度和压力场进行拟合,研究了不同辊速对牛顿和纯黏性流体流场的影响.
以上研究主要关注压延辊筒间隙内的流场,并没有考虑压延后黏弹性流体的胀大问题.对于橡胶来说,高分子的链弹性回复会造成压延后胶料出现胀大现象,这将直接影响后续产品尺寸.Zheng和Tanner[13]采用简化的单模态PTT流体模型计算了压延的速度压力场,并给出了出口的胀大变形情况.然而,单模态PTT流体模型在表征橡胶黏弹性行为时存在较大偏差,因此,难以获得准确的压延胀大比.此外,在建立压延过程的数值分析模型时,需要事先确定胶料与辊筒的分离点.对于非弹性流体(牛顿、幂律和宾汉流体)而言,分离条件为分离点处压力和压力梯度均为零,可以通过理论分析确定分离点的位置[6-8].然而对于黏弹性流体,由于弹性的存在则不能通过以上分离条件直接确定分离点.为此,Arcos等[14]根据上述分离条件采用迭代计算确定了单模态PTT流体模型下的分离点.而Zheng和Tanner[13]则提出了分离点处切应力为零的新分离条件,并用数值分析验证了单模态PTT模型下该分离条件的有效性.但需要指出的是,文献[13-14]的分离点确定方法对轮胎胶料这类更为复杂的黏弹性流体的压延过程模拟并不实用.
本文将利用Polyflow软件建立轮胎胶料压延过程的二维有限元模型,分别采用BC模型和五模态PTT模型表征胶料的纯黏性和黏弹性行为,并尝试提出确定黏弹性流体压延分离点的方法,通过数值模拟考察不同辊速下胶料的流动情况以及出口胶料变形情况,并与实测结果进行对比.
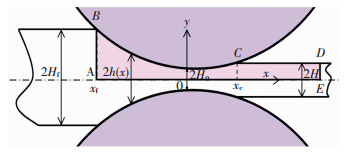
1 计算模型 1.1 控制方程图 1为压延过程示意图.其中,B点为胶料与辊筒的接触点;C点为胶料与辊筒的分离点;Hf为入口处胶料厚度的一半;H为出口胶料厚度的一半;H0为辊筒最小间隙的一半;h(x)为辊筒表面高度的一半;辊筒表面线速度为Vu;辊筒半径为R;胶料与辊筒接触点的横坐标为xf,胶料与辊筒分离时的横坐标为xc.
|
图 1 辊筒间隙的压延流动分析 Fig.1 Flow analysis of calendaring in clearance |
假设橡胶为不可压缩流体.在辊筒间隙内,胶料的流动为二维等温稳态流动,熔融胶料在辊筒壁处无滑移.流动时胶料的惯性力及重力忽略不计,可得出以下控制方程:
连续性方程
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0; $ |
X方向运动方程
| $ \rho u\frac{{\partial u}}{{\partial x}} + \rho v\frac{{\partial u}}{{\partial y}} = - \frac{{\partial P}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}}; $ |
Y方向运动方程
| $ \rho u\frac{{\partial v}}{{\partial x}} + \rho v\frac{{\partial v}}{{\partial y}} = - \frac{{\partial P}}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}}; $ |
边界条件
| $ \begin{array}{l} y = 0;{\tau _{yx}} = 0;\\ y = h\left( x \right);u = U. \end{array} $ |
本文研究对象是上下辊筒半径相等且辊速相同的压延机.由于对称性,取其1/2模型进行几何建模.模型由2个子区域组成,子区域1描述辊筒间隙内部的流动,子区域2描述流体通过辊筒间隙后的胀大行为.引入无量纲量
| $ \begin{array}{l} x' = \frac{x}{{\sqrt {2R{H_0}} }}, y' = \frac{y}{{{H_0}}}, \\ \frac{{h\left( {x'} \right)}}{{{H_0}}} = 1 + \frac{{{x^2}}}{{2R{H_0}}}, {x_{\rm{c}}}^\prime = \frac{{{x_{\rm{c}}}}}{{\sqrt {2R{H_0}} }}. \end{array} $ |
其中,xc′为无量纲化后的分离点横坐标.定义胶料胀大后稳定的厚度与辊筒间隙厚度的比值为胶料的厚度比.
压延过程包含无量纲变量的几何模型如图 2(a)所示.图中AB为胶料入口段,BC为辊筒表面,CD为胶料分离后的自由表面,DE为胶料出口段,AE为对称面.本文试算发现沿Y方向的第一层网格厚度以及C点右方第一排网格宽度对计算结果有较大影响.当上述网格尺寸逐渐减小时,胶料的胀大厚度逐渐趋于稳定.通过反复试算,本文建立的有限元网格模型如图 2(b)所示.

|
图 2 包含无量纲变量的几何模型 Fig.2 Models with dimensionless variables: (a)the geometric model; (b) the mesh model |
压延胶料的流变性能测试工作在橡胶加工分析仪(RPA2000)上进行,测量了3种不同温度下(80、100和120 ℃)和不同剪切速率下胶料的黏度.在此基础上,对胶料的流变性能进行纯黏性和黏弹性拟合[15-17],得出相应的材料参数.由于该胶料受温度影响较小[18],根据工厂实际压延工况,选用100 ℃下的测试结果进行拟合.
纯黏性模型(Bird-Carreau)本构方程为
| $ \mathit{\boldsymbol{\tau }} = 2\eta \mathit{\boldsymbol{D}}, $ | (1) |
| $ \eta = {\eta _\infty } + \left( {{\eta _0} - {\eta _\infty }} \right){\left[ {1 + {{\left( {\lambda \dot \gamma } \right)}^2}} \right]^{\frac{{n - 1}}{2}}}. $ | (2) |
式中:τ为应力张量;η为表观黏度;D为形变速率张量;η∞为极限剪切黏度;η0为零剪切黏度;λ为松弛时间;
| 表 1 BC模型的材料参数 Table 1 Material parameters of BC model |
黏弹性模型(Phan-Thien-Tanner)本构方程为
| $ \mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{T}}_1} + {\mathit{\boldsymbol{T}}_2}, $ | (3) |
| $ \exp \left[ \frac{{{\varepsilon }_{i}}{{\lambda }_{i}}}{{{\eta }_{1}}}\text{tr}\left( {{\mathit{\boldsymbol{T}}}_{1}} \right) \right]{{\mathit{\boldsymbol{T}}}_{1}}+{{\lambda }_{i}}\left[ \left( 1-\frac{{{\xi }_{i}}}{2} \right){{\overset{\nabla }{\mathop{\mathit{\boldsymbol{T}}}}\, }_{1}}+\frac{{{\xi }_{i}}}{2}{{\overset{\Delta }{\mathop{\mathit{\boldsymbol{T}}}}\, }_{1}} \right]=2{{\eta }_{1}}\mathit{\boldsymbol{D}}, $ | (4) |
| $ {\mathit{\boldsymbol{T}}_2} = 2{\eta _2}\mathit{\boldsymbol{D}}. $ | (5) |
其中
| $ {{\eta }_{1}}\text{=}\left( 1-{{\eta }_{\gamma }} \right)\eta , {{\eta }_{2}}={{\eta }_{\gamma }}\eta . $ |
式中:T为应力张量;T1为黏弹性应力分量;T2为纯黏性应力分量;D为形变速率张量;ε为与拉伸黏度相关的材料参数;ξ为与第二法向应力差相关的参数;△为下随体时间导数;▽为上随体时间导数;λ为松弛时间;ηγ为零剪切黏度中纯黏性分量的占比;η为零剪切黏度.
需要指出的是,对于PTT本构模型来说,模态数越多越能获得更好的拟合效果,但过多的模态数会造成后续计算成本的增加.因此,本文在能获得较好拟合结果的基础上,选择了五模态的PTT模型.拟合得到的相关参数如表 2所示.
| 表 2 PTT模型的材料参数 Table 2 Material parameters of PTT model |
压延模型的边界条件如图 2(a)所示,具体如下:
AB:入口边界条件(fn=fs=0);
BC:速度边界条件(Vs=Vu, Vn=0),辊筒速度Vu为0.01 m/min至10 m/min;
CD:自由表面;
DE:出口边界条件(fn=fs=0);
AE:对称边界条件(fs=0, Vn=0).
确定边界条件时,需要特别注意胶料与辊筒分离点C点的位置.分离点是压延模型关键参数,依赖于辊筒规格、辊距及物料本身的性质等.如何确定无量纲化后分离点的横坐标(xc′)一直以来都是研究压延过程的难点之一.对于非弹性流体,C点处应满足分离条件,即P=dP/dx=0.一些较为简单的流体本构模型,如牛顿模型、幂律模型和宾汉模型,根据润滑近似假设(LAT)可直接通过理论计算得出xc′的值.例如,牛顿流体的xc′为0.475.而对于更为复杂的模型,如BC模型,则无法直接求出xc′的值.
为解决复杂模型的分离点确定问题,Zheng和Tanner[13]提出将切应力为零作为分离条件,同时采用试错的方法,找出分离点C点的位置.即取不同的xc′,假设该点为分离点,并计算该处的切应力,若该点处的切应力为0,则将该点作为胶料与辊筒的分离点.以牛顿流体为例,用这种方法得出的xc′值和理论推导得出的结果相差约为1.05%,因此本文首先采用这种方法确定BC模型的分离点.保持辊筒速度不变(Vu=6 m/min),取不同的xc′值作为假设分离点的横坐标分别进行试算,最终得到该辊速下的xc′=0.498,且BC模型的分离点与辊筒速度无关.
对于黏弹性模型(PTT),采用有限元模拟时,材料本身的性质会造成分离点处存在一个非常大的应力[9]梯度,因此,对于本文中的黏弹性模型,将切应力为零作为判定条件并不适用.
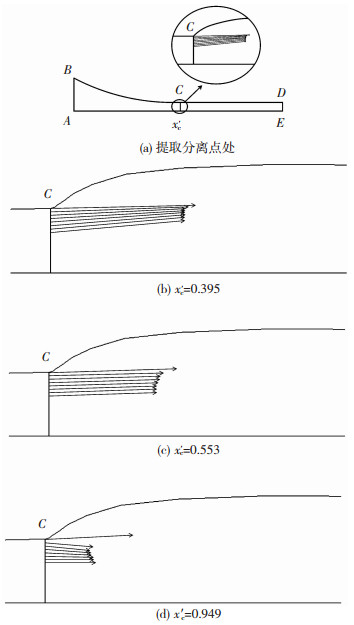
为确定合理的分离点,保持辊筒的速度不变(U=6 m/min),本文计算了一定范围内(0.316≤xc′≤1.028)的10个不同分离点下的压延流场.并以此为基础,尝试给出一个确定分离点坐标值的方法.具体如下:取分离点处的速度矢量进行分析,如图 3(a)所示.分离点C点左边为辊筒表面,C点右边为可以胀大的自由表面.C点处的速度大小与辊筒速度相同,速度方向与辊筒轮廓相切.图 3(b)、(c)、(d)分别为xc′=0.395、0.553和0.949时的速度矢量图.
|
图 3 假设分离点处的速度矢量 Fig.3 Velocity vector at the assumed separation point:(a)velocity vectorobtainedat the separation point; (b) xc′=0.395;(c)xc′=0.553;(d)xc′=0.949 |
由图 3可以看出,随着xc′的增加,C点下方附近的胶料流动方向由向上运动逐渐转变为向下运动.当C点下方附近的速度方向向上时,意味着假设分离点处的胶料还会跟随辊筒继续向上运动,即还未发生分离,此时假设分离点xc′的值小于实际分离点的值.当C点下方附近的速度方向向下时,意味着假设分离点处的胶料有向下运动的趋势,但这与实际并不相符.因为在实际的压延过程中,压出时的辊筒速度始终向上,不可能造成C点下方有向下运动的趋势.这种不合理的现象是由于强制的分离边界条件造成的,即此时已经发生了分离,xc′的值大于实际分离点的值.为保证胶料能被平稳均匀地压出,分离点处胶料流动的速度矢量应尽可能保持水平.为此给出确定分离点的判据为:当分离点处的速度矢量与水平方向一致时,xc′的值等于实际分离点的值.根据上述判据,本文得出分离点处的xc′为0.640.
需要指出的是,对于五模态PTT模型,随着辊速的增加,分离点有向左移动的趋势,但此变化对最终厚度比的影响较小(5%以内),因此本文后续均采用该xc′值对不同辊速下的压延过程进行计算.
3 计算结果与讨论为探究辊速对压延过程的影响,保持上一节获得的分离点xc′值不变,分别使用纯黏性模型和黏弹性模型进行数值模拟,考察不同辊速下的压延流场和自由胀大过程.
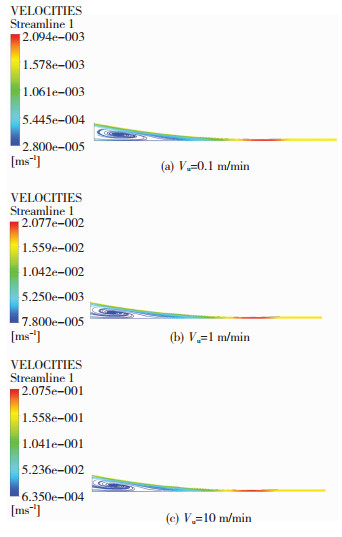
图 4为用BC本构模型计算得到的胶料在0.1、1和10 m/min辊速下的速度流线分布,可以看出,随着辊筒速度的增加,BC模型下的速度流线发生了细微的变化,但整体的分布方式未发生明显改变.就自由段变形来说,未观察到明显的胀大现象.
|
图 4 BC模型不同辊速下的流场和变形 Fig.4 Flow field and deformation at different roller speeds for BC model |
图 5为用PTT本构模型计算得到的胶料在0.1、1和10 m/min辊速下的速度流线分布,可以看出:随着辊筒速度的增加,PTT模型下的速度流线分布方式发生了明显的变化,胶料内部出现一个漩涡;自由段有明显的胀大变形,且厚度比随着辊筒速度增加而增大.

|
图 5 PTT模型不同辊速下的流场和变形 Fig.5 Flow field and deformation at different roller speeds for PTT model |
将计算得到的自由段厚度导出,发现胶料稳定后的厚度大于分离点处的胶料厚度,即胶料发生了胀大变形.
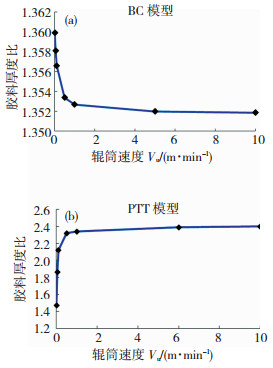
图 6(a)为BC模型的压延厚度比随辊筒速度的变化曲线,可以看出,BC模型厚度比基本上随着辊筒速度的增大而减小.由于不计及弹性,胀大的原因是速度场的重新分布.虽然BC模型能描述材料的剪切变稀特性,但其算出的厚度比过小,且随着辊筒速度的变化与实际不符,所以用BC模型来拟合橡胶类聚合物不合适.图 6(b)为PTT模型的厚度比随辊筒速度的变化曲线,可以看出,当辊筒速度较小(Vu≤0.5 m/min)时,模型的厚度比随着辊筒速度的增大而明显增大,这主要是由胶料的弹性恢复造成的.当辊筒速度逐渐升高(Vu≥0.5 m/min)时,厚度比增加的趋势逐渐趋于平缓.
|
图 6 两种模型厚度比随辊筒速度的变化关系 Fig.6 Relationship between the swell ratio and the roller speeds of the two models |
为考察计算结果有效性,采用塞尺和激光测厚仪分别对实际压延生产中的辊筒间隙和胶片厚度进行了测量,得到辊筒速度6 m/min下的胶料厚度比为2.875,而本文数值仿真得到的厚度比为2.389.仿真结果与实测结果基本吻合,但也存在一定偏差.
造成这一偏差可能的原因有:1)辊筒在工作状态时会承受压延胶料时的巨大压力,因此停机测量的辊筒间隙应比工作时的间隙偏小;2)本文所用的胶料参数是在100 ℃等温状态下测量得到,未考虑温度对胶料性质的影响,实际上胶料压延过程是一个非等温过程,本文忽略了温度场不均匀对压延过程造成的影响.此外,从图 6(b)可以看出,模拟得到的辊速6和10 m/min下的胶料厚度比几乎不变,这也与工厂实测结果一致.以上对比表明,在对橡胶这类弹性比较显著的非牛顿流体而言,在压延过程模拟中必须计及胶料的弹性,才能获得符合实际的结果.
4 结论1) 建立了轮胎胶料压延的二维有限元模型,提出了确定黏弹性流体压延分离点的方法,即假设不同分离点位置进行计算,当假设分离点处速度矢量与水平方向一致时,该点即为实际分离点.
2) 模拟结果发现,采用五模态PTT模型获得的胶料厚度比与实际测量值基本吻合,而采用BC模型的计算值则差异较大,这表明在压延模拟时必须计及胶料的弹性.
3) 研究了辊筒转速对胶料厚度比的影响,胶料厚度比在低辊速下随着辊速增加而迅速增大,在辊速较高时则趋于稳定.
致谢
感谢佳通轮胎(中国)研发中心为本文研究提供支持以及在胶料测试和压延实验方面提供帮助.
| [1] |
GASKELL R E. The calendering of plastic materials[J]. Journal of Applied Mechanics, 1950(17): 334-336. |
| [2] |
KELVEY J M. Polymer Processing[M]. New York: John Wiley and Sons, 1962.
|
| [3] |
CHONG J S. Calendering thermoplastic materials[J]. Journal of Applied Polymer Science, 1968, 12(1): 191-212. DOI:10.1002/app.1968.070120118 |
| [4] |
ALSTON W W, ASTILL K N. An analysis for the calendering of non-newtonian fuilds[J]. Journal of Applied Polymer Science, 1973(17): 3157-3174. |
| [5] |
BRAZINSKY I, COSWAY H F, JR C F V, et al. A theoretical study of liquid-film spread heights in the calendering of newtonian and power law fluids[J]. Journal of Applied Polymer Science, 1970, 14(11): 2771-2784. DOI:10.1002/app.1970.070141111 |
| [6] |
MIDLEMAN S. Fundamentals of Polymer Processing[M]. New York: McGraw Hill, 1977.
|
| [7] |
SOFOU S, MITSOULIS E. Calendering of pseudoplastic and viscoplastic sheets of finite thickness[J]. Journal of Plastic Film & Sheeting, 2004, 20(20): 185-222. |
| [8] |
SOFOU S, MITSOULIS E. Calendering of pseudoplastic and viscoplastic fluids using the lubrication approximation[J]. Journal of Polymer Engineering, 2004, 24(5): 505-522. |
| [9] |
MITSOULIS E. Numerical simulation of calendering viscoplastic fluids[J]. Journal of Non-Newtonian Fluid Mechanics, 2008, 154(2/3): 77-88. |
| [10] |
钱欣, 许王定, 金杨福. POLYFLOW基础及其在塑料加工中的应用[M]. 北京: 化学工业出版社, 2010.
|
| [11] |
LUTHER S, MEWES D. Three-dimensional polymer flow in the calender bank[J]. Polymer Engineering & Science, 2004, 44(9): 1642-1647. |
| [12] |
LUTHER S, MEWES D, SCHUSTER R H. Theoretical study of the three-dimensional flow field in the calender bank[C]//2003 International Mechanical Engineering Congress and Exposition. Washington, D.C.: ASME, 2003: 783-788.
|
| [13] |
ZHENG R, TANNER R I. A numerical analysis of calendering[J]. Journal of Non-Newtonian Fluid Mechanics, 1988, 28(2): 149-170. |
| [14] |
ARCOS J C, BAUTISTA O, MENDEZ F, et al. Theoretical analysis of the calendered exiting thickness of viscoelastic sheets[J]. Journal of Non-Newtonian Fluid Mechanics, 2012(177/178): 29-36. |
| [15] |
YANG C, LI Z. An integrated numerical study of coextrusion flow inside and outside the die[J]. Journal of Applied Polymer Science, 2016, 133(23): 43522. |
| [16] |
YANG C, LI Z. Effects of wall slip on the rheological measurement and extrusion die design of a filled rubber compound[J]. Plastics Rubber & Composites, 2016, 45(7): 326-331. |
| [17] |
YANG C, LI Z. A study of wall slip in the capillary flow of a filled rubber compound[J]. Polymer Testing, 2014, 37(8): 45-50. |
| [18] |
杨川.轮胎生产中挤出工艺的实验研究和数值模拟[D].合肥: 中国科学技术大学, 2016.
|
 2019, Vol. 27
2019, Vol. 27


