分形是一门以非规则几何形态为研究对象的几何学[1-3],分形几何学的建立,引起各学科领域专家学者的关注.大量研究表明,金相组织的晶粒具有分形结构,可以用分形维数对其形貌进行描述[4-6].分形维数的计算方法通常有相似性维数[7]、质量分形维数[8]、Euclid维数[9]、计盒维数[10]等.计盒维数以其简单及易于实现的特点,而被广泛采用.
目前,对于组织分形研究已经取得了一定成果.Kobayashi[11]等利用晶界分形来优化GBE以及对晶粒结构(大小和形状)的考察,并用来判断SUS316L奥氏体不锈钢的晶间腐蚀路径扩展.该文采用盒维数法计算了具有最大连贯性随机晶界的分形维数,发现随机晶界数目越多,其分形维数越大,晶界耐腐蚀性越差.Usov等[12]对不同化学成分材料进行冲击-弯曲试验,同样采用盒维数法计算了试样微观形貌的分形维数,并得到了分形维数与冲击韧性、弯曲度、屈服强度以及极限强度之间的计算公式,将微观形貌与宏观性能联系起来.张青等[13]对热变形Ti-15-3合金再结晶晶粒的分形进行了研究,对比了小岛法和盒维数法计算方法,发现两者差别不大.此外,还有大量文献[14-18]中涉及到晶界的分形维数计算讨论,晶界节点作为晶界交叉处,对材料性能的影响不可忽视[19-20],但针对晶界节点的分形是否存在的研究较少.
本文将以低碳钢冷轧薄板标样铁素体晶粒金相组织为研究对象,利用MATLAB图像处理功能和基于计盒维数法原理自行开发的分形维数计算程序,对晶界节点的分形维数是否存在进行探究.同时,为考察工艺参数对晶界节点分形维数的影响,以耐腐性要求较高的Pb-Ca-Sn-Al合金为试验材料,对其不同工艺条件下晶界节点分形维数进行了研究.
1 确定晶界节点分形维数是否存在基于GB/T4335《低碳钢冷轧薄板铁素体晶粒度测定法》中标准图,为了保证视野中晶界节点的数目不因太少而失去准确度,每组标准下选取6到9级晶粒度金相图像,经过MATLAB图像处理功能,以晶粒延伸度为1的晶粒度为9的金相图片为例,采用改进的分水岭方法[21]将晶界节点提取出来,如图 1所示.其中图 1(a)为原始金相组织图,为了去掉边界的影响,在其中截取了最大的一部分,见图 1(b),图 1(f)是经MATLAB图像处理并将晶界节点提取后的图像.

|
图 1 晶粒度为9、延伸度为1的金相图处理 Fig.1 Metallographic pattern processing with a grain size of 9 and an elongation of 1:(a)original metallographic organization; (b)partial view; (c)watershed mark map; (d)binarization; (e)grain boundary node processing |
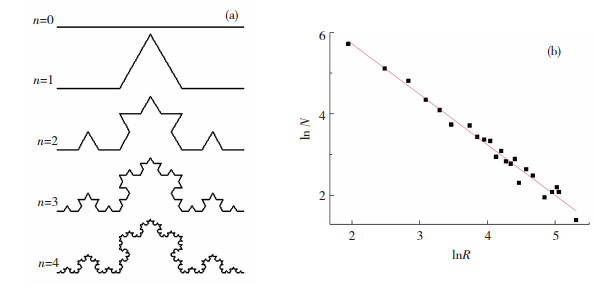
为确定上述标准样晶界节点的分形维数是否存在,利用MATLAB软件编写了基于计盒维数法的原理计算程序.为验证程序的准确性,引入“Koch曲线”这一经典曲线,如图 2所示.“Koch曲线”作为标准分形图,用相似维数的定义计算出的维数约为1.261 78,而利用计程序计算得到Koch曲线分形维数为1.267 68,其中横坐标是盒子尺寸的对数(lnR,R是盒子的尺寸),纵坐标是盒子数目的对数(lnN,N指覆盖了分形图像的盒子),与理论值几乎没有差别,可以认为该程序计算是准确的.
|
图 2 Koch曲线(a)及其拟合结果(b) Fig.2 Koch curve (a) and its fitting results (b) |
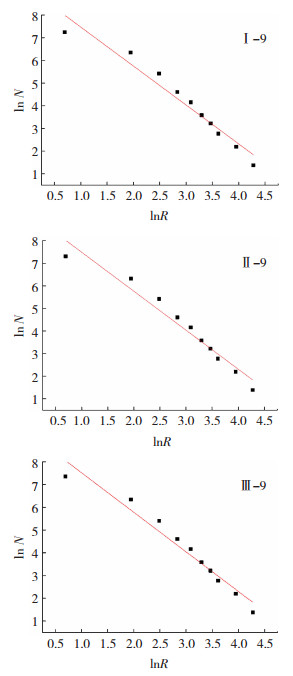
图 3是3种晶粒延伸度下(Ⅰ:晶粒延伸度为1,Ⅱ:晶粒延伸度为2,Ⅲ:晶粒延伸度为3)晶粒度为9的分形维数拟合结果,3种拟合结果的直线相关系数均达到97%以上.以Ⅰ—9为例,在显著性水平α=0.001下,通过F分布表查得临界值Fσ(1.8)=25.42,观测值F0= 153.948 92,F0≫Fα,故回归方程是显著的.Ⅱ—9和Ⅲ—9与Ⅰ—9是类似的,那么lnN与lnR存在线性关系的,即晶界节点的分形维数是存在的.表 1是经过MATLAB分形计算程序得到不同标准下不同晶粒度级别的铁素体晶界节点的分形维数.
|
图 3 3种标准下晶粒度为9的晶界节点分维 Fig.3 Fractal dimension of grain boundary node with grain size 9 under three standards |
| 表 1 不同晶粒度级别下晶界节点的分形维数 Table 1 Fractal dimension of grain boundary nodes at different levels of grain size |
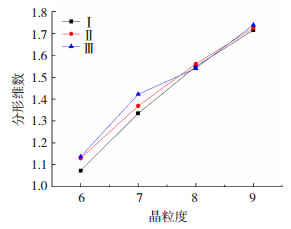
图 4为不同标准不同晶粒度晶界节点分形维数的比较,可以看出,在同一延伸度下,随着晶粒度的增加,晶界节点的分形维数是增加的;在晶粒度较小时,分形维数随着延伸度的增加而增加,晶粒度较大时,晶界节点的分形维数相对接近.
|
图 4 不同标准不同晶粒度晶界节点分形维数 Fig.4 Fractal dimensions of grain boundary nodes with different standards and grain sizes |
为讨论其他工艺参数对晶界节点分形维数的影响,针对不同工艺条件下的Pb-Ca-Sn-Al合金晶界节点的分形维数进行计算.试验所用试样为Pb-Ca-Sn-Al合金,其化学成分如表 2所示.本试验的轧制部分在异步轧机上进行,试验所用轧机的轧辊为Φ110 mm×155 mm,其异速比i可调(
| 表 2 Pb-Ca-Sn-Al合金化学成分(质量分数/%) Table 2 Chemical composition of Pb-Ca-Sn-Al alloy(wt.%) |
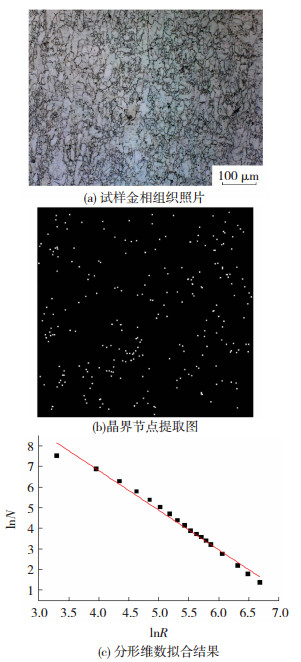
为研究不同工艺参数对Pb-Ca-Sn-Al合金晶界节点分形维数的影响,设置单因素试验,得到试样金相组织.分维计算方法:以任意一组试验试样的金相图为例,按照标准样的图形处理方法,得到晶界节点提取图,并通过计算程序得到其分维值,如图 5所示,其中,图 5(b)为MATLAB图形处理后晶界节点提取图,为了显示效果,将背景调成黑色,晶界节点为白色.
|
图 5 试样分形维数计算示例 Fig.5 Example of sample fractal dimension calculation:(a)sample metallographic photo; (b)grain boundary node extraction map; (c)fractal dimension fitting result |
拟合得到该金相组织图的分形维数为1.918 66,拟合度为98.41%,且符合F检验.由图 5可以看到, Pb-Ca-Sn-Al合金晶界节点分形维数是存在的.针对不同工艺下Pb-Ca-Sn-Al合金晶界节点分形维数,选取5~8张200倍放大倍数下的金相图进行计算,取其平均值,结果如图 6所示.
|
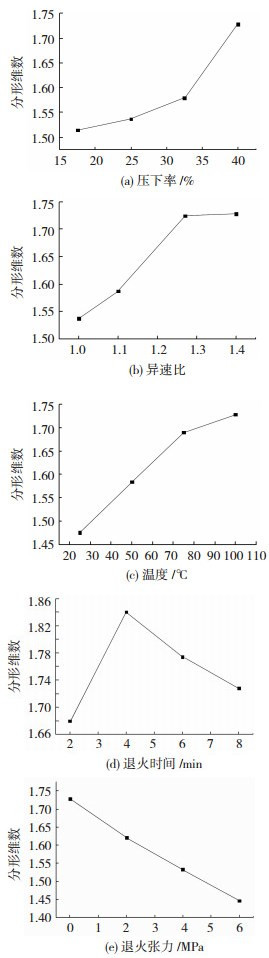
图 6 不同工艺参数对Pb-Ca-Sn-Al合金晶界节点分形维数的影响 Fig.6 Effect of different process parameters on the fractal dimension of grain boundary nodes of Pb-Ca-Sn-Al alloy:(a)reduction rate; (b)allometric ratio; (c)temperature; (d)annealing time; (e)annealing tension |
图 6(a)是异速比为1.4、退火张力为0、退火温度100 ℃、退火时间为8 min不同压下率下晶界节点分形维数变化曲线;图 6(b)是压下率为40%、退火张力为0、退火温度100 ℃、退火时间为8 min不同异速比下晶界节点分形维数变化曲线;图 6(c)是压下率40%、异速比为1.4、退火张力为0,退火时间为8 min不同退火温度下晶界节点分形维数变化曲线;图 6(d)是压下率40%、异速比1.4、退火张力为0、退火温度为100 ℃不同退火时间下晶界节点分形维数变化曲线;图 6(e)是压下率为40%、异速比1.4、退火温度100 ℃、退火时间为8 min不同退火张力下晶界节点分形维数变化曲线.
由图 6可以看出,在一定范围内随着压下率、异速比、退火温度的增加,晶界节点的分形维数随之增加;退火时间增加,Pb-Ca-Sn-Al合金晶界节点分形维数先上升后下降;退火张力增加,晶界节点分形维数下降.
2.3 结果分析由上述分析可以得到, Pb-Ca-Sn-Al合金晶界节点分形维数与其再结晶密切相关.通常静态再结晶可采用Avrami方程描述:
| $ X_{\alpha}=1-\exp \left[-B\left(\frac{t}{t_{0.5}}\right)^{n}\right] $ | (1) |
式中:Xα为静态再结晶软化率; B,n为材料常数; t为再结晶时间(s); t0.5为再结晶体积分数为50%时的停留时间(s); t0.5取决于温度T(K)、应变εeq、应变速率
| $ {t_{0.5}} = A{\varepsilon _{{\rm{eq}}}}^p\dot \varepsilon _{{\rm{eq}}}^q{D^s}{\rm{exp}}\frac{Q}{{RT}} $ | (2) |
式中:A、p、q、s均为材料常数;Q为激活能,J/mol;R为气体常数,J/(mol·K).
根据式(1)和式(2),随着压下率、退火温度、退火时间的增加,通常再结晶百分数是增加的,再结晶越充分,晶粒越细小,晶界节点的分形维数是增加的.本试验条件下压下率和温度对Pb-Ca-Sn-Al合金晶界节点分形维数的影响符合一般规律,但退火时间对其影响则有违常规.这是由于在高压下率、高温退火(铅合金熔点低,在327 ℃以下)条件下,Pb-Ca-Sn-Al合金在较短的时间内完成大部分再结晶,此时分形维数较大,随后,再结晶晶粒逐渐长大,分形维数下降.
异速比对Pb-Ca-Sn-Al合金晶界节点分形维数的影响则是由于异步轧制的特性造成的.异步轧制中上下轧辊与轧件接触的摩擦力的方向不同会形成一个搓轧区.在搓轧区中剪切应力的存在会使得位错更容易开动和攀移,再结晶也就越充分,晶界节点的分形维数越大.退火中施加张力,会对晶界迁移产生影响,已有相关文献证明[22-23].对Pb-Ca-Sn-Al合金来说, 张力是起阻碍作用的[24],延缓再结晶,其晶界节点分形维数随着退火张力的增加而下降.
3 结论1) 晶界节点的分形维数是存在的.
2) 不同工艺参数对Pb-Ca-Sn-Al合金晶界节点分形维数的影响如下:在一定范围内,随着压下率、异速比、退火温度的增加,晶界节点的分形维数随之增加;退火时间增加,Pb-Ca-Sn-Al合金晶界节点分形维数先上升后下降;退火张力增加,晶界节点分形维数下降.
| [1] |
曹晓卿. 分形理论在金属材料研究中的应用[J]. 太原理工大学学报, 1999, 30(2): 133-135. CAO Xiaoqing. Application of fractal theory in the study of metal materials[J]. Journal of Taiyuan University of Technology, 1999, 30(2): 133-135. DOI:10.3969/j.issn.1007-9432.1999.02.007 |
| [2] |
文洪杰, 彭达岩. 分形理论在材料研究中的应用和发展[J]. 钢铁研究报, 2000, 12(5): 70-73. WEN Hongjie, PENG Dayan. Application and development of fractal theory in materials research[J]. Steel research report, 2000, 12(5): 70-73. DOI:10.3321/j.issn:1001-0963.2000.05.017 |
| [3] |
徐炜新, 苏建红, 谢崇津. 分形理论在金相学中的应用[J]. 理化检验:物理分册, 2008, 44(7): 349-353. XU Yixin, SU Jianhong, XIE Chongjing. Application of fractal theory in metallography[J]. Physical and chemical inspection:Physical Volume, 2008, 44(7): 349-353. |
| [4] |
LEHOCKEY E M, PALUMBO G, LIN P, et al. On the relationship between grain boundary character distribution and intergranular corrosion[J]. Scripta Materialia, 1997, 36(10): 1211-1218. DOI:10.1016/S1359-6462(97)00018-3 |
| [5] |
郭洪民, 杨湘杰. 凝固微观组织的多层次模拟[J]. 中国有色金属学报, 2004, 14(6): 928933. GUO Hongmin, YANG Xiangjie. Multi-level simulation of solidified microstructure[J]. Chinese Journal of Nonferrous Metals, 2004, 14(6): 928933. DOI:10.3321/j.issn:1004-0609.2004.06.009 |
| [6] |
GLASS H J, WITH G D. Fractal characterization of the compaction and sintering of ferrites[J]. Materials Characterization, 2001, 47(1): 27-37. DOI:10.1016/S1011-5803(01)00148-6 |
| [7] |
MANDELBROT B. How Long Is the Coast of Britain Statistical Self-Similarity and Fractional Dimension[J]. Science, 1967, 156(3775): 636. DOI:10.1126/science.156.3775.636 |
| [8] |
PERFECT E. Estimating soil mass fractal dimensions from water retention curves 1[J]. Geoderma, 1999, 88(s3-4): 221-231. DOI:10.1016/S0016-7061(98) |
| [9] |
HAN Z, CHEN Y, FU Y. Studying relationships between the fractal dimension of the drainage basins and some of their geomorphological characteristics[J]. International Journal of Geosciences, 2013, 4(3): 636-642. DOI:10.4236/ijg.2013.43058 |
| [10] |
BISWAS M K, GHOSE T, GUHA S, et al. Fractal dimension estimation for texture images: A parallel approach[J]. Pattern Recognition Letters, 1998, 19(3-4): 309-313. DOI:10.1016/S0167-8655(98)000026 |
| [11] |
KOBAYASHI S, KOBAYASHI R, WATANABE T. Control of grain boundary connectivity based on fractal analysis for improvement of intergranular corrosion resistance in SUS316L austenitic stainless steel[J]. Acta Materialia, 2016, 102: 397-405. DOI:10.1016/j.actamat.2015.08.075 |
| [12] |
USOV V V, RABKINA M D, SHKATULYAK N M, et al. Fractal dimension of grain boundaries and mechanical properties of the metal of oxygen cylinders[J]. Materials Science, 2015, 50(4): 1-9. DOI:10.1007/s11003-015-9761-8 |
| [13] |
张青, 李萍, 薛克敏. 热变形Ti-15-3合金再结晶晶粒的分形分析[J]. 中国有色金属学报, 2007, 17(7): 1149-1154. ZHANG Qing, LI Ping, XUE Kemin. Fractal analysis of recrystallized grains of hot deformed Ti-15-3 alloy[J]. Chinese Journal of Nonferrous Metals, 2007, 17(7): 1149-1154. DOI:10.3321/j.issn:1004-0609.2007.07.021 |
| [14] |
XU M, CHEN J, LU H, et al. Effects of residual stress and grain boundary character on creep cracking in 2.25Cr-1.6W steel[J]. Materials Science & Engineering A, 2016, 659: 188-197. DOI:10.1016/j.msea.2016.02.025 |
| [15] |
KOBAYASHI S, TSUREKAWA S, WATANABE T. A new approach to grain boundary engineering for nanocrystalline materials[J]. Beilstein Journal of Nanotechnology, 2016, 7: 1829-1849. DOI:10.3762/bjnano.7.176 |
| [16] |
ZÖLLNER Dana. Topology of grain microstructures in two dimensions: a comparison of grain boundary and triple junction controlled grain growth[J]. Modelling & Simulation in Materials Science & Engineering, 2014, 22(22): 25-28. DOI:10.1088/0965-0393/22/2/025028 |
| [17] |
王静, 吴希俊. 三叉结点对铜-铋三晶断裂行为的影响[J]. 物理学报, 1993, 42(12): 1963-1967. WANG Jing, WU Xijun. Effect of trigeminal junction on the deformation behavior of Cu-Nb tricrystal[J]. Journal of Physics, 1993, 42(12): 1963-1967. |
| [18] |
张其阳, 刘国奇, 杨帅明, 等. 改进的分水岭算法在牛乳体细胞上的分割及应用[J]. 无线互联科技, 2017(5): 101-102. ZHANG Qiyang, LIU Guoqi, YANG Shuaiming, et al. Segmentation and application of improved watershed algorithm on bovine milk cells[J]. Wireless Internet Technology, 2017(5): 101-102. DOI:10.3969/j.issn.1672-6944.2017.05.045 |
| [19] |
LIM A T, HAATAJA M, CAI W, et al. Stress-driven migration of simple low-angle mixed grain boundaries[J]. Acta Materialia, 2012, 60(3): 1395-1407. DOI:10.1016/j.actamat.2011.11.032 |
| [20] |
李德超, 董俊慧, 陈海鹏, 等. 退火张力对无取向硅钢再结晶织构和磁性能的影响[J]. 材料导报, 2017(2): 92-95. LI Dechao, DONG Junhui, CHEN Haipeng, et al. Effect of annealing tension on recrystallization texture and magnetic properties of non-oriented silicon steel[J]. Material Guide, 2017(2): 92-95. DOI:10.11896/j.issn.1005-023X.2017.02.020 |
| [21] |
李彬.张力作用下Pb-Ca-Sn-Al合金再结晶模型与组织模拟的研究[D].武汉: 武汉科技大学, 2015. LI Bing.Study on Recrystallization Model and Microstructure Simulation of Pb-Ca-Sn-Al Alloy under Tension[D].Wuhan: Wuhan University of Science and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10488-1015582487.htm |
 2019, Vol. 27
2019, Vol. 27


