合金的最大固溶度,取决于溶剂、溶质的原子结构,以及由此引起的原子间作用能的改变程度.其中表征物理能的是畸变能,表征化学能的有电负性、电离能、亲和能等.固溶度大小是多种因素综合作用的结果,难以用量子力学进行定量计算.运用热力学理论,将固溶度同电负性、原子半径、价电子浓度等因素联系起来的半经验方法,仍然起着主导作用.其中主要是Hume-Rothery法则和在其基础上建立的Darken-Garry图[1-2].
1 H-R法则与D-G图合金固溶体分为置换型和间隙型两类.关于置换型固溶体,20世纪30年代英国冶金学家Hume-Rothery经多年研究总结出影响固溶度的3条经验规律[1-8].
1) 尺寸因素.溶质与溶剂的原子大小不同引起晶格畸变,达到一定值将使固溶体变得不稳定.通常, 原子半径差△Ra<15%(高熔点溶剂, △Ra<8%~10%),才有利于获得“显著”固溶度(≥5% mol).
2) 电负性效应.两组元的电负性差越大,越容易形成稳定化合物,从而限制它们之间的固溶度,通常电负性差△N<0.4,才有可能获得“显著”固溶度.
3) 相对价效应.两个组元原子价不同,以低价元素为溶剂的固溶度,通常大于以高价元素为溶剂的固溶度.
其中,1)和2)具有普遍性但不是充分条件,只说明在多数情况下满足则有可能获得“显著”固溶度.
后续研究发现,价电子浓度也是决定固溶度极限的重要因素,最大固溶度对应于一定的价电子浓度,超过该浓度固溶体便失去稳定性[1].
1953年Darken-Garry根据Hume-Rothery法则,绘制以原子半径和电负性为判据的二维图用于预测固溶度,称Darken-Garry图[1-2],开创了用图形预测固溶度的先河,为合金设计提供依据.继Darken-Garry图后出现的其他预测图[2],虽然在某些方面有所改进,却各有不足,目前普遍应用的仍是Darken-Garry图.
Darken-Garry图以原子半径差-电负性差为判据预测合金固溶度.溶质与溶剂的原子半径不同,会引起晶格畸变能的增加,促使固溶体不稳定.以原子半径差△Ra=±15%为临界值适用于大多数合金.原子半径按定义分为:轨道半径、范德华半径、共价半径、金属半径.预测合金固溶度,溶质为金属元素采用金属半径,非金属元素采用共价半径.为消除晶型对金属半径的影响,按配位数12修正为标准的哥德斯密德原子半径(Goldschmid atomic radius)R(CN=12)[9],非金属元素半径采用单键共价半径Rc(1)[10].
D-G图采用的是鲍林电负性.1932年鲍林提出,以氟的电负性为4.0,锂的电负性为1.0,计算其他元素的相对电负性,作为原子在分子中对成键电子的吸引能力的量度.它适用于判断元素的金属性和非金属性、化合物中元素化合价的正负,以及化合物分子的键型、共价键的极性[10-11],而用于预测合金固溶度,是认为元素的电负性差越大,越容易形成化合物,从而限制它们之间的固溶度[1].
Darken-Garry图,以横坐标表示原子半径,纵坐标表示电负性;以溶剂元素为中心点,标出待测的溶质元素点;按照Weber建议以摩尔分数5%区分固溶度的大和小[2]选取临界值(原子半径差△Ra=±15%、电负性差△N =±0.4),通过4个临界点作矩形或椭圆形;然后,以溶质元素是否落在边界线内,来判断能否获得“显著”(≥5%)固溶度.
原子半径差正确反映了晶格畸变能影响固溶度的实际,保证了预测的正确率,而电负性却导致预测正确率低[2].电负性对于主族元素来说有明显的变化规律,同一周期从左到右递增,同一族自上而下递减,金属元素与非金属元素分列于周期表的左右,因此,适于判断离子键或共价键化合物的形成倾向.而对处于中部的大量副族元素来说,变化无规律,难以适用于以金属键结合为主的合金固溶度的判断.除电负性外,表征电化学效应的还有价电子浓度、电离能、亲和能等.其中电离能可以定量地比较原子失去电子的难易程度,是原子的核电荷、电子排布和原子半径多个因素综合作用的结果,更能反映元素原子之间的结合强度,从而胜任合金固溶度的判据.据此提出创建A-I图的方案, 通过796个合金系对D-G图和A-I图的预测正确率进行比较.
2 A-I图的建立电离能是气态的基态原子失去一个电子所需要的最小能量,常用I表示,单位为kJ/mol.失去一个电子生成+1价阳离子所需要的能量称为第一电离能,再失去一个电子称第二电离能, 依此类推[10-11].以下均指第一电离能.
溶质与溶剂的电离能越接近越有利于互溶,差值加大则降低固溶度.根据大量合金系已知固溶度元素的统计结果,选取电离能差的临界值.
建立A-I图的具体方法:以原子半径Ra为横坐标、电离能Ei为纵坐标,以溶剂元素为中心点,标出待测的溶质元素点;以摩尔分数5%界定固溶度大小设定判据的临界值(原子半径差取△Ra=±15%,电离能差取△Ei=±20%,),通过4个临界点平行坐标轴作矩形;然后, 以是否落在边界线内来预测能否获得“显著”的固溶度.图 1为Ta合金的A-I图,建图所需数据取自文献[9-15].
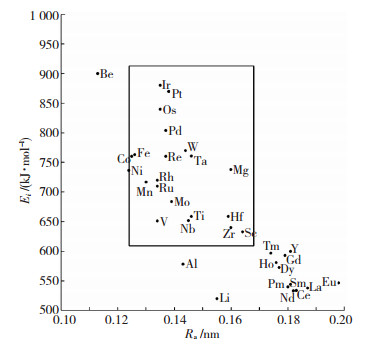
|
图 1 Ta合金的A-I图 Fig.1 A-I diagram of Ta alloys |
从元素周期表ⅡA—ⅤA、ⅠB—ⅦB、Ⅷ12个族中,选择得到较多应用的元素,如Mg、Al、Cu、Ti、V等20个元素作溶剂组元,若干已知固溶度的元素作溶质,组成796个合金系对D-G图与A-I图进行比较,同时兼顾可溶与不可溶元素的预测正确率.对于固溶度≥5%的元素,以落入边界线内为正确;<5%的元素,以落在边界线外为正确.
D-G图:原子半径差△Ra=±15%,电负性差△N =±0.4椭圆形边界;
A-I图:原子半径差△Ra=±15%,电离能差△Ei=±20%,矩形边界.
D-G图采用椭圆形,是基于尺寸因素和电负性因素都处于边缘条件的溶质,难以获得较大固溶度的推理,并未被证实,也不像Gschneidner指出的:“使用矩形会使预测可溶元素的准确率有所下降,而预测不溶元素的准确率会略有升高,椭圆形优于矩形”[2].
事实上,使用矩形相当于放宽边界条件,使可溶元素的预测正确率升高,不可溶元素的预测正确率降低,各有利弊.A-I图采用矩形参与验证,与D-G图的比较结果见表 1.
| 表 1 D-G图与A-I图预测错误统计 Table 1 Statistics of error prediction by D-G diagram and A-I diagram |
根据表 1对预测错误的统计:固溶度≥5%的可溶元素共289个,按照D-G图,落在椭圆形外的142个,预测错误率为49%.其中落在椭圆形与外切矩形之间的有24个,减去这部分(相当于以矩形边为分界线),预测错误率将降至41%.按照A-I图,落在矩形外的79个,预测错误率为27%.两种情况,D-G图比A-I图的预测错误率分别高22%和14%.
固溶度<5%的不可溶元素共507个,按照D-G图,落在椭圆形内的55个,预测错误率为11%.落在椭圆形与外切矩形之间的有26个,加上这部分(相当于以矩形边为分界线),预测错误率将升至16%.按照A-I图,落在矩形内的80个,预测错误率为16%.D-G图采用椭圆形边界线,预测错误率比A-I图低5%,采用矩形边界线二者相等.表明在对不可溶元素预测错误率相等的条件下,对可溶元素,A-I图比D-G图的预测错误率低14%,可见作为预测固溶度的判据,电离能优于电负性.
4 结语1) A-I图比D-G图提高了预测正确率,对于副族元素尤为显著.
2) 电离能比电负性更胜任预测合金固溶度判据的角色.
3) 采用椭圆形边界线,使可溶元素的预测错误率升高,不可溶元素的预测错误率降低.
| [1] |
余永宁. 金属学原理[M]. 北京: 冶金工业出版社, 2000: 76-78.
|
| [2] |
张邦维, 廖树帜. 合金固溶度理论研究的进展[J]. 上海金属, 1999, 21(3): 5-7. |
| [3] |
MIZHTANI U. Hume-Rothery rules for structural complex alloy phases[M]. Britain Taylor & Francis Group, 2010.
|
| [4] |
HOSFORD William F. Physical Metallurgy[M]. Second Edition. Boca Raton: CRC Press, 2010.
|
| [5] |
Wikipedia Encyclopedia.Hume-Rothery Rules[EB/OL].[2018-04-30].https://en.wikipedia.org/wiki/Hume-Rothery_rules.
|
| [6] |
HICKS M. Engine Materials[EB/OL].(2012-10-25).https://wenku.baidu.com/view/2f1d677e31b765ce05081416.html
|
| [7] |
张晓燕. 材料科学基础[M]. 2版. 北京: 北京大学出版社, 2014: 26-29.
|
| [8] |
郑子樵. 材料科学基础[M]. 2版. 长沙: 中南大学出版社, 2013: 38-41.
|
| [9] |
潘金生, 田民波. 材料科学基础[M]. 北京: 清华大学出版社, 1998: 90-92.
|
| [10] |
夏少武, 夏树伟. 结构化学[M]. 北京: 科学出版社, 2012: 71.
|
| [11] |
薛冬峰, 李克艳, 张方方. 材料化学进展[M]. 上海: 华东理工大学出版社, 2011: 3-9.
|
| [12] |
黎文献. 镁及镁合金[M]. 长沙: 中南大学出版社, 2005: 76-88.
|
| [13] |
朱莉雅.二元合金系固溶体固溶度的计算化学研究与预报[D].上海: 上海大学, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1150519
|
| [14] |
BRANDES E A, BROOK G B. Smithells Metals Reference Book[M]. London: London Butterworths, 1992: 404-882.
|
| [15] |
《材料科学技术百科全书》委员会. 材料科学技术百科全书[M]. 北京: 中国大百科全书出版社, 1995: 3-4.
|
 2019, Vol. 27
2019, Vol. 27


