由于吸波材料能够有效吸收电磁波,并减少电磁波反向散射,有望用于飞行器的隐身技术、微波暗室、电磁兼容等方面而受到人们的广泛关注[1-3].理想的吸波材料应满足如下性能:吸波频段宽、吸收能力强、质量轻、吸波涂层厚度薄.因此,人们致力于开发具有高磁导率和高磁损耗的新型微波吸收材料[4-6].在铁磁性纳米片中,交换能、偶极能和各向异性能之间存在着复杂的竞争.因此, 这种结构化介质的静态和动态性能与构成材料的固有磁特性、各个元素的形状尺寸及纳米片间相互作用等有着密切的关系[7-9].已有研究表明, 具有低于临界厚度的单层铁磁薄膜可以显示一个良好限定的均匀铁磁共振模型[10].坡莫合金纳米带通常存在两种共振模式,“块体”共振模式和“边缘”共振模式[11-12].矩形铁磁性纳米片长宽比越大,则“块体”模式的强度越强.随着矩形比逐渐减小,低频共振峰峰高会变得大于高频共振峰峰高,最终出现一个明显共振峰和一些微小共振峰[13].但关于两纳米片的相对位置、纳米片间距、磁各向异性方向对铁磁性纳米片微波磁性影响的研究鲜有报道.本文提出了多纳米片结构,其具有较强的形状各向异性和高磁导率, 通过调节纳米片的相对位置、纳米片间距、磁各向异性方向展宽磁共振峰的峰宽,使其能有效地工作在一个较宽的吸收频带.
1 微磁学理论及模拟方法在微磁学模拟中,磁介质表示为宏观连续体,其特征取决于依赖空间和时间的磁化强度M(ri, t),且在恒温下磁化矢量模为常数,即|M(ri, t)|=Ms.通过求解Landau-Lifshitz-Gilbert (LLG)常微分方程获得磁化分布的演变.
| $ \begin{array}{*{20}{c}} {\frac{{\partial \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right)}}{{\partial t}} = - \gamma \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right) \times {\mathit{\boldsymbol{H}}_{{\rm{eff}}}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right) + }\\ {\frac{\alpha }{{{M_{\rm{s}}}}}\mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right) \times \frac{{\partial \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right)}}{{\partial t}}.} \end{array} $ | (1) |
式中:M(ri, t)为磁化强度矢量;γ为旋磁比(γ取2.21×105 m/(A·s));α为阻尼系数;Heff(ri, t)为有效场(包括交换场、磁晶各向异性场、退磁场和外磁场),它是吉布斯自由能对磁极化强度的负数微分,即
| $ {\mathit{\boldsymbol{H}}_{{\rm{eff}}}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right) = - \frac{1}{{{\mu _0}}}\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right)}}. $ | (2) |
吉布斯自由能E由4个能量项组成(忽略弹性势能和表面各向异性能):交换能、磁晶各向异性能、退磁能和Zeeman能(外场能)[14-15].首先在未加外磁场情况下,通过求解时域中的磁化运动方程(LLG),获得磁体的静态磁矩分布.然后,采用静态磁矩分布作为初始状态,计算铁磁性纳米片的高频响应.为了计算与弱交变外磁场δh(t)相关的线性磁响应δm(ri, t),磁化强度和有效场分别由静态部分和小的动态扰动组成[7-12].
| $ \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right) = {\mathit{\boldsymbol{M}}_{{\rm{eq}}}}\left( {{\mathit{\boldsymbol{r}}_i}} \right) + \delta \mathit{\boldsymbol{m}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right), $ | (3) |
| $ {\mathit{\boldsymbol{H}}_{{\rm{eff}}}}\left( {{\mathit{\boldsymbol{r}}_\mathit{i}}, t} \right) = {\mathit{\boldsymbol{H}}_{{\rm{eq}}}}\left( {{\mathit{\boldsymbol{r}}_i}} \right) + \delta \mathit{\boldsymbol{h}}(t) + {\mathit{\boldsymbol{H}}_{{\rm{eq}}}}\left( {\delta \mathit{\boldsymbol{m}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right)} \right). $ | (4) |
且
| $ \begin{array}{l} \frac{{\partial \delta \mathit{\pmb{m}}}}{{\partial t}} = - \gamma \left\{ {\delta \mathit{\pmb{m}} \times {\mathit{\boldsymbol{H}}_{{\rm{eq}}}}\left( {{\mathit{\boldsymbol{r}}_i}} \right) + {\mathit{\boldsymbol{M}}_{{\rm{eq}}}}\left( {{\mathit{\boldsymbol{r}}_i}} \right) \times [\delta \mathit{\boldsymbol{h}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{H}}_{{\rm{eq}}}}(\delta \mathit{\boldsymbol{m}})]} \right\} + \frac{\alpha }{{{\mathit{\boldsymbol{M}}_\rm{s}}}}{\mathit{\boldsymbol{M}}_{{\rm{eq}}}}\left( {{\mathit{\boldsymbol{r}}_i}} \right) \times \frac{{\partial \delta \mathit{\pmb{m}}}}{{\partial t}}. \end{array} $ | (5) |
对于一个给定的弱交变场δh(t),式(4)的解允许访问交变磁化强度δm(ri, t),其中交变磁化强度δm(ri, t)是交变外磁场δh(t)和磁化率χ(ri, t)的卷积.
| $ \delta \mathit{\boldsymbol{m}}\left( {{\mathit{\boldsymbol{r}}_i}, t} \right) = \chi \left( {{\mathit{\boldsymbol{r}}_i}, t} \right)*\delta \mathit{\boldsymbol{h}}(t). $ | (6) |
通过快速傅里叶变换(Fast Fourier Transform,FFT)可以将式(6)变换到频域,
| $ \delta \mathit{\pmb{m}}\left( {{\mathit{\pmb{r}}_i}, \mathit{\pmb{\omega}}} \right) = \chi \left( {{\mathit{\pmb{r}}_i}, \mathit{\pmb{\omega}}} \right)*\delta \mathit{\pmb{h}}(\mathit{\pmb{\omega}}). $ | (7) |
为了减小非线性行为,通过外加一个弱的交变磁场激励系统来获得磁化率.
| $ \delta h(t) = 7.96\exp ( - 7.675t). $ |
式中:t为时间,ns;h为磁场强度,A/m.上式通过快速傅里叶变换得到
| $ \delta h(\omega ) = 7.96/(7.675 + 2{\rm{ \mathsf{ π} }}i\omega ) $ |
其中,ω为交变磁场的固定频率,GHz.这种形式有高达20 GHz的频率响应,可计算得到这个频率的磁化率[10-12],且该交变磁场在矩形铁磁性纳米片内是一个空间均匀的场.
本文选择尺寸为100 nm×80 nm×4 nm的单个矩形铁磁性纳米片作为参考对象,如图 1(a)所示.其本征磁参数设置如下:饱和磁化强度Ms=0.8×106A/m,交换作用常数A=1.3×10-11J/m,磁晶各向异性常数K=4.8×103J/m3,易轴取向沿矩形铁磁纳米片的宽度[12-13].仿真时采用的网格单元大小为4 nm×4 nm×4 nm(网格尺寸小于材料的交换长度
|
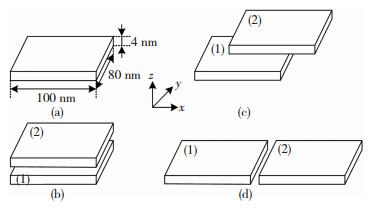
图 1 仿真对象模型图:(a)单个矩形纳米片模型;(b)上下平行排列的两个矩形纳米片模型;(c)上下平行且有相对位移的两个矩形纳米片模型;(d)左右平行排列的两个矩形纳米片模型 Fig.1 Simulation object model: (a) single rectangular nanosheet model; (b) two rectangular nanosheet models arranged parallel to each other; (c) two rectangular nanosheet models arranged up and down with relative displacements; (d) two rectangular nanosheet models arranged parallel to each other |
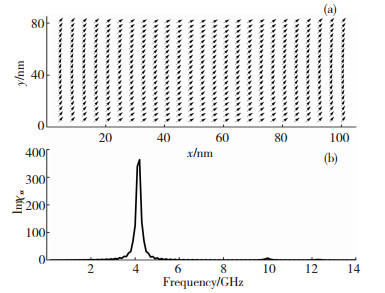
首先,计算单个矩形铁磁性纳米片的静态磁矩分布和磁谱,如图 2所示.从图 2(a)可以看出,矩形铁磁性纳米片长轴中间部分的磁矩偏离长轴,并与长轴呈45°排列,而长轴两端的磁矩趋向于沿短轴方向,且纳米片所有区域中的相邻磁矩彼此几乎都趋于平行.在铁磁性纳米片体系中,磁晶各向异性有利于磁矩平行或反平行于易轴,交换作用使相邻磁矩平行排列,而退磁相互作用使得矩形铁磁性纳米片两端的磁矩偏离矩形铁磁性纳米片的长轴.各向异性能、交换能和退磁能的竞争最终导致一个不均匀的磁化状态,见图 2(a).从图 2(b)可以看出,磁谱由一个频率为4.2 GHz的强共振峰和一个频率为10 GHz的弱共振峰组成,这是由纳米片边缘和纳米片中间的局部有效场变化引起的.
|
图 2 单个矩形铁磁性纳米片的静态磁矩分布(a)和磁化率(Imχxx)虚部(b) Fig.2 Equilibrium configuration (a)and imaginary part of susceptibility (Imχxx)(b)of single rectangular ferromagnetic nanosheets |
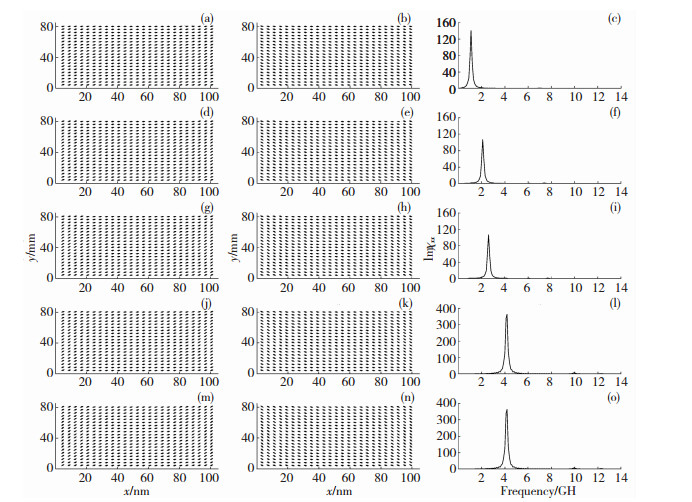
图 3为相距分别为1、2、3、4、5 nm的上下平行排列的两个矩形铁磁性纳米片的静态磁矩分布和磁谱.图 3(a)、(d)、(g)、(j)、(m)分别为相距1、2、3、4、5 nm的上下平行排列的两个矩形铁磁性纳米片的下部分,图 3(b)、(e)、(h)、(k)、(n)分别为相距1、2、3、4、5 nm的上下平行排列的两个矩形铁磁性纳米片的上部分.比较图 3(a)、(d)、(g)、(j)、(m),发现其静态磁矩分布非常相似,纳米片长轴中间部分的磁矩都倾向于沿长轴方向排列,纳米片长轴两端的磁矩稍偏离长轴方向,且相邻磁矩彼此几乎趋于平行.同样,图 3的(b)、(e)、(h)、(k)、(n)与图 3(a)、(d)、(g)、(j)、(m)的静态磁矩分布相似,只是磁矩方向相反.这是交换能、退磁能、各向异性能共同决定的总自由能取最小值的体现.图 3(c)、(f)、(i)、(l)、(o)分别为相距1、2、3、4、5 nm的上下平行排列的两个矩形铁磁性纳米片的磁谱,可以看到,磁谱都是由一个较低频率的强共振峰和一个较高频率的弱共振峰组成,这是由纳米片边缘和纳米片中间的局部有效场变化引起的,并且,随着两矩形铁磁性纳米片之间距离的增加,磁谱的主共振峰随之增大,接近于单个矩形铁磁性纳米片的磁谱的主共振峰(图 2(b)).这可能是由于随着两纳米片之间距离变大,两纳米片之间的相互作用变小,当两纳米片间的距离增大到一定程度,它们之间不存在相互作用,相当于两个单个矩形铁磁性纳米片.相距4、5 nm时,强共振峰与单个矩形铁磁性纳米片的磁谱的主共振峰(4.2 GHz)相同.说明从相距大于4 nm时,两矩形铁磁性纳米片相当于两个彼此独立的单矩形铁磁性纳米片.
|
图 3 图 1中(b)模型的静态磁矩分布和磁谱 Fig.3 Equilibrium configurations and the imaginary parts of susceptibility of the (b) model in Fig. 1 |
图 4为磁各向异性方向分别呈0°、30°、45°、60°、90°的上下平行排列的两个矩形铁磁性纳米片(两纳米片上下相距1 nm)的静态磁矩分布和磁谱.图 4(a)、(d)、(g)、(j)、(m)分别为磁各向异性方向呈0°、30°、45°、60°、90°的上下平行排列的两个矩形铁磁性纳米片的下部分(即图 1(b)中的(1)部分)的静态磁矩分布.图 4(b)、(e)、(h)、(k)、(n)分别为磁各向异性方向呈0°、30°、45°、60°、90°的上下平行排列的两个矩形铁磁性纳米片的上部分(即图 1(b)中的(2)部分)的静态磁矩分布.从图 4(a)、(b)、(d)、(e)的静态磁矩分布中可以看出,除磁矩方向不同外,磁矩几乎都倾向于沿长轴方向排列,只有纳米片长轴两端的磁矩稍微偏离长轴方向.图 4(c)、(f)分别为磁各向异性方向分别呈0°、30°的上下平行排列的两个矩形铁磁性纳米片的磁谱,两图中磁谱都只有一个较低频率的共振峰,且频率和峰值几乎相同.这说明当改变两个矩形铁磁性纳米片的磁各向异性方向所呈角度较小时,对矩形铁磁性纳米片的磁性能的影响可以忽略不计.从图 4(g)、(j)、(m)的静态磁矩分布可以发现,所有磁矩都偏离长轴方向且与长轴呈45°排列.图 4(h)、(k)、(n)中的静态磁矩分布也是如此,只是磁矩的方向与图 4(g)、(j)、(m)中磁矩的方向相反.图 4(i)、(l)、(o)分别为磁各向异性方向分别呈45°、60°、90°的上下平行排列的两个矩形铁磁性纳米片的磁谱.比较图 3(c)、(f)与(i)可以发现,其磁谱都由一个强共振峰和多个弱共振峰组成,且主共振峰移动到一个较高的频率8.5 GHz上.说明两个矩形铁磁性纳米片的磁各向异性方向所呈角度由45°增加到90°时,对矩形铁磁性纳米片的磁性能的影响变化不大.由上述结果可以得出,随着两个矩形铁磁性纳米片的磁各向异性方向所呈角度由30°增加到45°,其磁谱的主共振峰随之由2.2 GHz增加到8.5 GHz.

|
图 4 磁各向异性方向分别呈0°、30°、45°、60°、90°的上((b)、(e)、(h)、(k)、(n))下((a)、(d)、(g)、(j)、(m))平行排列的两个矩形铁磁性纳米片的静态磁矩分布和磁谱((c)、(f)、(i)、(l)、(o)) Fig.4 Equilibrium configurations and the imaginary parts of susceptibility Imχxx of two parallel rectangular ferromagnetic nanosheets with the magnetic anisotropic directions at 0°, 30°, 45°, 60°and 90°, respectively |
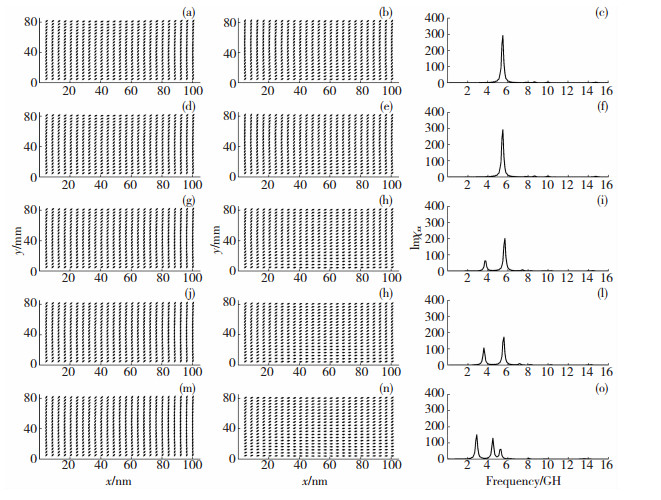
图 5为磁各向异性方向分别呈0°、30°、45°、60°、90°的上下平行排列且有相对位移(上部分相对下部分x轴位移40 nm,y轴位移48 nm)的两个矩形铁磁性纳米片(两纳米片上下相距1 nm)的静态磁矩分布和磁谱.图 5(a)、(d)、(g)、(j)、(m)分别为磁各向异性方向呈0°、30°、45°、60°、90°的上下平行排列且有相对位移的两个矩形铁磁性纳米片的下部分(即图 1(c)中的(1)部分)的静态磁矩分布.图 5(b)、(e)、(h)、(k)、(n)分别为磁各向异性方向呈0°、30°、45°、60°、90°的上下平行排列且有相对位移的两个矩形铁磁性纳米片的上部分(即图 1(c)中的(2)部分)的静态磁矩分布.从图 5(a)、(b)、(d)、(e)的静态磁矩分布可以发现,纳米片短轴中间部分的磁矩几乎都倾向于沿短轴方向排列,纳米片短轴两端的磁矩偏离长轴方向且与长轴呈45°排列,且这4个磁谱中的磁矩的方向一致.图 5(c)、(f)分别为磁各向异性方向分别呈0°、30°的上下平行排列且有相对位移的两个矩形铁磁性纳米片的磁谱.比较图 5(c)与图 2(a)可以发现,图 5(c)磁谱的主共振峰移动到一个较高的频率5.5 GHz上.说明两纳米片间的相互作用对纳米片磁性能的影响有所增加.比较图 5(f)与图 5(c)发现, 磁谱的主共振峰没有明显变化.说明当改变两个矩形铁磁性纳米片的磁各向异性方向所呈角度较小时,对矩形铁磁性纳米片的磁性能的影响不大.
|
图 5 磁各向异性方向分别呈0°、30°、45°、60°、90°的上((b)、(e)、(h)、(k)、(n))下((a)、(d)、(g)、(j)、(m))排列且有相对位移的两个矩形铁磁纳米片的静态磁矩分布和磁谱((c)、(f)、(i)、(l)、(o)) Fig.5 Equilibrium configurations and the imaginary parts of susceptibility Imχxx of the two rectangular ferromagnetic nanosheets with relative displacement and the magnetic anisotropy directions at 0°, 30°, 45°, 60°and 90°, respectively |
同样,图 5(g)、(j)、(m)的静态磁矩分布中纳米片短轴中间部分的磁矩几乎都倾向于沿短轴方向排列,纳米片短轴两端的磁矩偏离长轴方向且与长轴呈45°排列,它们磁谱中磁矩的方向一致且彼此平行.但是,图 5(h)、(k)、(n)的静态磁矩分布中纳米片长轴中间部分的磁矩几乎都倾向于沿长轴方向排列,纳米片长轴两端的磁矩偏离长轴方向且与长轴呈45°排列,它们磁谱中磁矩的方向一致且彼此平行.图 5(i)、(l)、(o)分别为磁各向异性方向分别呈45°、60°、90°的上下平行排列且有相对位移的两个矩形铁磁性纳米片的磁谱.从图 5(i)中可看出,磁谱虚部存在3个共振峰,频率分别为3.6、5.1、7.5 GHz,它们的峰宽约为1.5 GHz.图 5(l)与图 5(i)比较,共振峰的数目相同,频率分别为3.6、5.1、7.2 GHz,其中频率为3.6 GHz的共振峰峰值比图 5(i)中频率为3.6 GHz的共振峰峰值高.图 5(n)磁谱的共振峰频率分别为3、4.5、5.5 GHz,由于频率相近而产生交叠,在一定意义上相当于增大了共振峰的峰宽,整体峰宽约为4 GHz.本文推测两个矩形铁磁性纳米片的磁谱存在多个共振峰可能是由于其内部存在多个不同大小的局域有效场,由于改变两纳米片的相对位置以及磁各向异性方向,破坏了纳米片原有较为均匀的有效场,导致了更加不均匀的场强分布.
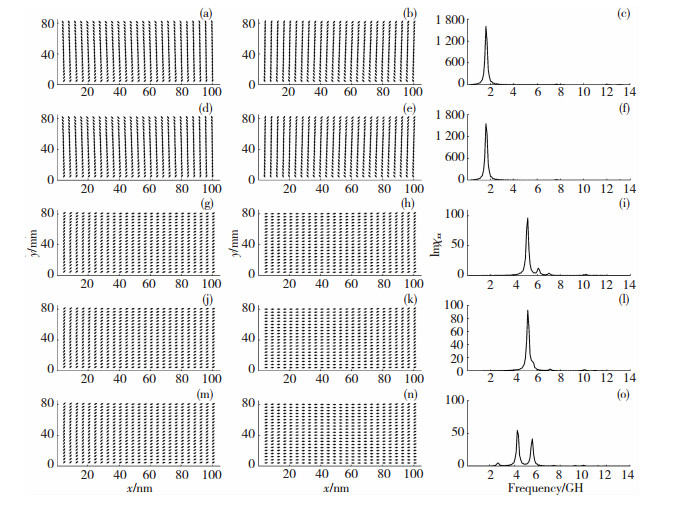
图 6为磁各向异性方向分别呈0°、30°、45°、60°、90°的左右平行排列的两个矩形铁磁性纳米片(左右两纳米片相距1 nm)的静态磁矩分布和磁谱.图 6(a)、(d)、(g)、(j)、(m)分别为磁各向异性方向呈0°、30°、45°、60°、90°的左右平行排列的两个矩形铁磁性纳米片的下部分(即图 1(d)中的(1)部分)的静态磁矩分布.图 6(b)、(e)、(h)、(k)、(n)分别为磁各向异性方向呈0°、30°、45°、60°、90°的左右平行排列的两个矩形铁磁性纳米片的上部分(即图 1(d)中的(2)部分)的静态磁矩分布.从图 6(a)、(b)、(d)、(e)的静态磁矩分布可以发现,纳米片短轴中间部分的磁矩几乎都倾向于沿短轴方向排列,纳米片短轴两端的磁矩偏离长轴方向且与长轴呈45°排列,但两端的磁矩方向相反,类似一个C形.图 6(c)、(f)分别为磁各向异性方向分别呈0°、30°的左右平行排列的两个矩形铁磁性纳米片的磁谱.从图 6(c)、(f)可以发现,磁谱的主共振峰峰值高达1500,这可能是因为找到的是一个亚稳态状态.图 6(g)、(h)、(j)、(k)、(m)、(n)的静态磁矩分布中磁矩几乎都倾向于沿长轴方向排列,两端的磁矩稍偏离长轴方向排列,其磁谱中的磁矩方向一致且彼此平行.图 6(i)、(l)、(o)分别为磁各向异性方向分别呈45°、60°、90°的左右平行排列的两个矩形铁磁性纳米片的磁谱.从图 6(i)可看出,磁谱虚部存在3个相距很近的共振峰,频率分别为5、6、7 GHz,整体峰宽约为4 GHz.图 6(l)与图 6(i)比较,频率为5、6 GHz的共振峰交叠在一起,邻近的还有一个频率为7 GHz的较小的共振峰.图 6(n)磁谱的共振峰频率分别为2.5、4.5、5.5 GHz,由于频率相近而产生交叠,增大了共振峰的峰宽,整体峰宽约为4 GHz.
|
图 6 图 1中(d)模型在不同磁各向异性方向下的静态磁矩分布和磁谱 Fig.6 Equilibrium configurations and the imaginary parts of susceptibility of the (d) model in Fig. 1 in different directions of magnetic anisotropy |
1) 相对位置、纳米片间距影响两矩形铁磁性纳米片共振峰频率的分布,当两矩形纳米片磁各向异性方向所呈角度由0°增加到30°时,其磁性质没有明显的变化,而从30°到90°时,其磁性质对磁各向异性方向变化比较敏感.
2) 改变两个矩形铁磁性纳米片的磁各向异性方向所呈角度,可显著影响磁损耗峰的数目、强度、峰宽和频率分布.因此,可以通过改变纳米片相对位置、纳米片间距及磁各向异性方向调控铁磁性纳米片的磁性质.可用于制备具有各种频率和较宽吸收频带的微波吸收材料.
| [1] |
TANG X, HU K. Preparation and electromagnetic wave absorption properties of Fe-doped zinc oxide coated barium ferrite composites[J]. Materials Science and Engineering: B, 2007, 139(2): 119-123. DOI:10.1016/j.mseb.2007.01.052 |
| [2] |
HAN Mangui, GUO Wei, WU Yanhui, et al. Electromagnetic wave absorbing properties and hyperfine interactions of Fe-Cu-Nb-Si-B nanocomposites[J]. Chinese Physics B, 2014, 23(8): 083301. DOI:10.1088/1674-1056/23/8/083301 |
| [3] |
HAN Z, LI D, WANG H, et al. Broadband electromagnetic- wave absorption by FeCo/C nanocapsules[J]. Applied Physics Litters, 2009, 95: 023114. DOI:10.1063/1.3177067 |
| [4] |
涂宽, 韩满贵. 磁性多孔纳米片微波磁导率的微磁学研究[J]. 物理学报, 2015, 64(23): 237501-237501. TU Kuan, HAN ManGui. Micromagnetics simulation on the microwave permeability of magnetic porous nano-flakes[J]. Acta Phys Sin, 2015, 64(23): 237501-237501. DOI:10.7498/aps.64.237501 |
| [5] |
周克省, 黄可龙, 孔德明, 等. 吸波材料的物理机制及其设计[J]. 中南工业大学学报, 2001, 32(6): 617-621. ZHOU Kesheng, HUANG Kelong, KONG Deming, et al. Physical mechanism and design of materials with electromagnetic wave absorption function[J]. J Cent South Univ Technol, 2001, 32(6): 617-621. DOI:10.3969/j.issn.1672-7207.2001.06.017 |
| [6] |
SNOKE J L. Dispersion and absorption in magnetic ferrites at frequencies above one Mc/s[J]. Physica, 1948, 14(4): 207-217. DOI:10.1016/0031-8914(48)90038-X |
| [7] |
VUKADINOVIC N. High-frequency response of nanostructured magnetic materials[J]. Journal of Magnetism and Magnetic Materials, 2009, 321(14): 2074-2081. DOI:10.1016/j.jmmm.2009.01.049 |
| [8] |
FIOVIK V, MACIA F, HERNANDEZ J M, et al. Tailoring the magnetodynamic properties of nanomagnets using magnetocrystalline and shape anisotropies[J]. Physical Review B, 2015, 92(10): 104406. DOI:10.1103/PhysRevB.92.104406 |
| [9] |
YAMAGUCHI M, KIM K H, IKEDAA S. Soft magnetic materials application in the RF range[J]. Journal of Magnetism and Magnetic Materials, 2006, 304(2): 208-213. DOI:10.1016/j.jmmm.2006.02.143 |
| [10] |
YOUSSEF J B, VUKADINOVIC N, BILLET D, et al. Thickness-dependent magnetic excitations in Permalloy films with nonuniform magnetization[J]. Physical Review B, 2004, 69(17): 174402. DOI:10.1103/PhysRevB.69.174402 |
| [11] |
GERARDIN O, LE G H, DONAHUE M J, et al. Micromagnetic calculation of the high frequency dynamics of nano-size rectangular ferromagnetic stripes[J]. Journal of Applied Physics, 2001, 89(11): 7012-7014. DOI:10.1063/1.1360390 |
| [12] |
LIU R L, WANG J B, LIU Q F, et al. Micromagnetic simulation of the magnetic spectrum of ferromagnetic nanowire[J]. Journal of Applied Physics, 2008, 103(1): 013910. DOI:10.1063/1.2829817 |
| [13] |
CHEN J H, CHEN J W, TANG D M, et al. Micromagnetic studies on magnetic spectra of submicron ferromagnetic particles with different aspect ratio[J]. Phys, Lett, 2010, 374: 620. DOI:10.1016/j.physleta.2009.11.029 |
| [14] |
VUKADINOVIC N, LABRUNE M, YOUSSEF J B, et al. Ferromagnetic resonance spectra in a weak stripe domain structure[J]. Physical Review B, 2001, 65(5): 054403. DOI:10.1103/PhysRevB.65.054403 |
| [15] |
RIVKIN K, HEIFET A, SIEVERT P R, et al. Resonant modes of dipole-coupled lattices[J]. Physical Review B, 2004, 70(18): 184410. DOI:10.1103/PhysRevB.70.184410 |
 2019, Vol. 27
2019, Vol. 27


