焊缝起始点自动导引技术是实现智能焊接机器人自动焊接的重要前提[1-3].大多数工业生产中应用的焊接机器人[4-5]主要采用示教-再现的工作方式,操作精度完全依赖于示教经验,且改变待焊工件的位置需重新示教,劳动强度大,工作效率低.目前,焊接起始点自动导引技术的研究并不多见.传统基于视觉的焊接初始位置三维信息的获取方法主要为立体视觉的方法[6-8],该方法是根据双目视觉原理利用摄像机在不同位置获得目标点的图像,经过图像处理、立体匹配、空间定位等过程计算目标点的三维坐标,进而控制机器人向目标点运动.而立体标定和立体匹配的算法复杂,且摄像机需要多次变换位置对目标点景物进行图像采集,为减小相机畸变的影响,需要尽量防止目标点位于视野边缘,操作过程较为繁琐.近年来,采用单目视觉的焊缝起始点位置识别的研究中包含的模板匹配、角点检测等算法停留在图像处理的层面上[9-11],仅检测出了目标点在成像平面上的二维坐标,无法满足实际焊接的要求.
针对以上问题,本文提出了一种十字激光单目视觉的两步导引法,利用单目视觉的图像处理技术确定目标点的二维位置信息,调整摄像机姿态使目标点位于摄像机坐标系z轴上;结合十字激光发生器,控制机器人沿摄像机坐标系z轴向目标点运动,对焊缝起点位置进行快速精确的导引.
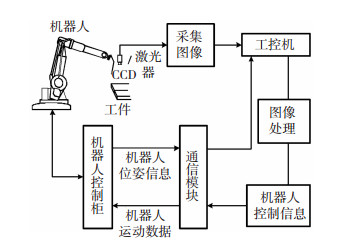
1 系统结构与前期工作采用Eye-in-hand的方式固定CCD摄像机采集被测工件的图像,机器人为瑞士ABB公司的IRB 1410型工业机器人,与工控机之间的通信采用其内置的Interface模块实现.CCD摄像机与十字激光器采用标准的结构光安装方式,注意在固定过程中尽量使十字激光交叉线与摄像机光轴位于同一平面.试验工件为2块50 mm×180 mm、厚度5 mm的普通碳钢平板对接成的v型坡口样件.试验装置如图 1所示,工控机为系统的主要控制核心,承担了图像采集、图像处理、数据运算及机器人运动状态的读取和控制等工作.
|
图 1 试验装置示意图 Fig.1 Schematic of test device |
由于该试验中的导引为一个由远及近的过程,首先,控制机器人位于工件上方一定距离,并保证焊缝起始点在摄像机视野范围内;然后,对采集到的图像进行Hough直线检测,求取直线交点的方法获得焊缝起始点的图像坐标[12],为后续的导引工作做准备.
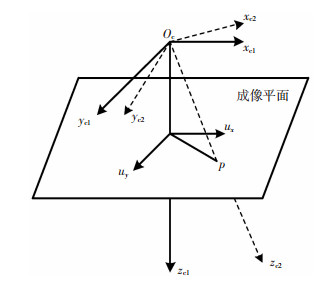
2 摄像机坐标系的姿态调整根据焊缝起始点在成像平面的坐标,建立如图 2所示的新坐标系,并求取新旧坐标系之间的转换关系.
|
图 2 坐标系转换 Fig.2 Conversion chart of coordinate |
焊缝起始点P在摄像机坐标系中的坐标为(xc, yc, f),其中f为相机焦距,xc、yc为P点在成像平面上的坐标,光源中心Oc与图像中目标点P可确定一条直线,设直线方程为
| $ \frac{x}{{{x_{\rm{c}}}}} = \frac{y}{{{y_{\rm{c}}}}} = \frac{z}{f}. $ | (1) |
对式(1)进行归一化处理,则该直线的单位向量可用式(2)表示:
| $ \frac{1}{{\sqrt {\left( {x_{\rm{c}}^2 + y_{\rm{c}}^2 + {f^2}} \right)} }}\left( {{x_{\rm{c}}}, {y_{\rm{c}}}, f} \right). $ | (2) |
以向量OP作为新坐标系的z轴,根据光源中心点O(0, 0, 0)、点(0, 0, f)以及点(xc, yc, f)决定的平面的垂向量按右手定则确定新坐标系的x轴与y轴,令两坐标系间转换矩阵为Rot
| $ \mathit{\boldsymbol{Rot}} = \left[ {\begin{array}{*{20}{l}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}} \end{array}} \right], $ | (3) |
| $ \frac{1}{{\sqrt {\left( {x_\text{c}^2 + y_\text{c}^2 + {f^2}} \right)} }}\left[ {\begin{array}{*{20}{c}} {{x_\text{c}}}\\ {{y_\text{c}}}\\ f \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]. $ | (4) |
由式(4)结合坐标系绕空间中任意一轴旋转的旋转矩阵[3],即可求得转换矩阵Rot:
| $ \mathit{\boldsymbol{Rot}} = \left[ {\begin{array}{*{20}{c}} {\frac{{y_\text{c}^2}}{m}{f_n} + \frac{f}{{\sqrt n }}}&{\frac{{ - {x_{\rm{c}}}{y_{\rm{c}}}}}{m}{f_n}}&{\frac{{{x_{\rm{c}}}}}{{\sqrt n }}}\\ {\frac{{ - {x_\text{c}}{y_{\rm{c}}}}}{m}{f_n}}&{\frac{{x_{\rm{c}}^2}}{m}{f_n} + \frac{f}{{\sqrt n }}}&{\frac{{{y_{\rm{c}}}}}{{\sqrt n }}}\\ {\frac{{ - {x_{\rm{c}}}}}{{\sqrt n }}}&{\frac{{ - {y_{\rm{c}}}}}{{\sqrt n }}}&{\frac{f}{{\sqrt n }}} \end{array}} \right]. $ | (5) |
式中,
| $ \left\{ {\begin{array}{*{20}{l}} {m = x_{\rm{c}}^2 + y_{\rm{c}}^2, }\\ {n = x_{\rm{c}}^2 + y_{\rm{c}}^2 + {f^2}, }\\ {{f_n} = 1 - \frac{f}{{\sqrt n }}.} \end{array}} \right. $ | (6) |
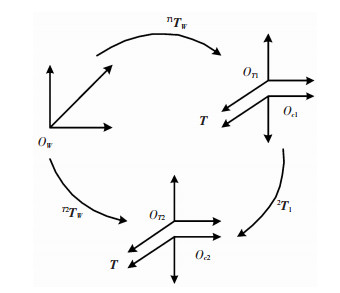
利用上述推导的旋转矩阵对机器人进行姿态变换,如图 3所示,W为机器人基坐标系,T1、T2分别为机器人运动前后机器人末端坐标系,c1、c2分别为机器人运动前后相机坐标系,摄像机坐标系与工具坐标系的转换矩阵T为常量矩阵,由两步标定法可以求解[13];T1TW、T2TW为世界坐标系与运动前后工具坐标系之间的转换矩阵,2T1为运动前后摄像基坐标系间的转换矩阵,存在如下关系:
| $ ^{T2}{\mathit{\boldsymbol{T}}_W} = {\mathit{\boldsymbol{T}}^{ - 1}} \cdot \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Rot}}}&0\\ 0&1 \end{array}} \right] \cdot \mathit{\boldsymbol{T}}{ \cdot ^{T1}}{\mathit{\boldsymbol{T}}_n}. $ | (7) |
|
图 3 系统坐标转换关系 Fig.3 Diagram of coordinate transformation |
经过2T1的变换,控制机器人运动即可使焊缝起始点在摄像机光轴上.
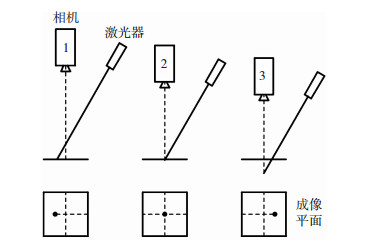
3 光轴方向的导引焊枪向目标点接近的过程中,由CCD摄像机拍摄获得的图像可知,激光交点不断向图像中心移动,如图 4所示,随着光点的不断靠近,焊枪距焊缝起始点的距离也是一个由远及近的过程.在调整摄像机姿后,十字激光交点可能没有出现在视野范围或距离图像中心较远.为节省计算时间,可通过激光点距离图像中心较远和较近两种控制模式对机器人进行控制,通过判断激光点是否出现在图像中对控制模式进行转换.
|
图 4 激光点位置示意图 Fig.4 Map of laser spot location |
导引过程主要对光轴方向上机器人移动的距离进行判定,假设机器人每次移动距离d,工具坐标系也在光轴方向上位移d,此时在得知机器人初始位姿矩阵iTW的情况下,即可对下一时刻的位姿进行估计,由式(7)可知:
| $ ^{i + 1}{\mathit{\boldsymbol{T}}_W} = {\mathit{\boldsymbol{T}}^{ - 1}} \cdot \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&{kd}\\ 0&0&0&1 \end{array}} \right] \cdot \mathit{\boldsymbol{T}}{ \cdot ^i}{\mathit{\boldsymbol{T}}_W}. $ | (8) |
式中,系数k随着工具坐标系在光轴方向的位移变化不断进行调整.
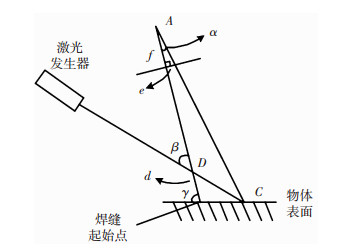
3.2 激光点距离图像中心较近的引导系统精确导引的原理如图 5所示,图中d即为需要向焊缝起始点移动的距离,f为焦距,AD为激光平面与摄像机坐标系轴交点坐标的矢量,β为激光器与摄像机光轴夹角,e为激光点在图像坐标系中距图像中心的距离,γ为光轴与工件平面夹角.其中,e、β、f、γ均为已知,AD可利用基于机器人运动和平面约束的激光平面方程标定方法[14]求得,三角形几何关系为
| $ |AC| = |AD|\cos \alpha + \frac{{|AD|\sin \alpha }}{{\tan (\beta - \alpha )}}, $ | (9) |
| $ d=|AD|\left( \varepsilon \left( 1-\tan \alpha \tan \left( {{90}^{{}^\circ }}-\alpha \right) \right)-1 \right). $ | (10) |
|
图 5 精确导引原理图 Fig.5 Principle diagram of precise guidance |
式中,
| $\alpha = \arctan \frac{e}{f}, $ | (11) |
| $ \varepsilon = {\cos ^2}\alpha + \frac{{\sin (2\alpha )}}{{2\tan (\beta - \alpha )}}. $ | (12) |
根据式(8),即可对焊枪的移动距离进行精确导引.
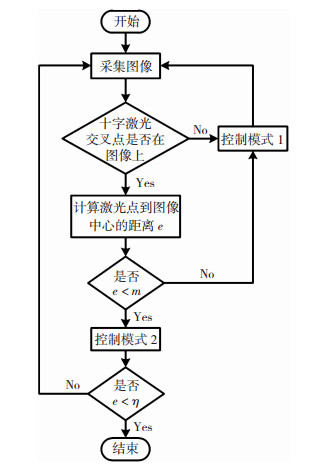
3.3 系统控制策略系统沿光轴方向导引的控制过程如图 6所示,控制模式1为激光点距离图像中心较远的导引,这个过程只是单一的控制机器人按给定的步长沿摄像机坐标系z轴向被测工件以较快速度靠近.控制模式2为激光点距离图像中心较近的引导,该模式下需要实时计算实际移动距离与给定步长之间的关系确定系数k,控制机器人进行精确导引.
|
图 6 系统控制流程图 Fig.6 Flow chart of system control |
系统的控制过程中设置了2个阈值.阈值m用来判断控制模式的转换,即使十字激光交点出现在图像视野中,但它到图像中心的距离大于阈值m则依然采用控制模式1,以此来减少不必要的计算,节省导引时间;阈值η用来判断导引结果,当激光点到图像中心的距离小于该参数时停止导引,避免导引过程中存在的细小误差使程序运行错误.
4 试验分析焊缝起始点导引试验系统如图 7所示.首先,进行机器人手眼标定[15]以及十字激光单一平面方程参数标定,求解相机坐标系相对于机器人末端坐标系的转换矩阵T和摄像机坐标系下的激光平面方程.
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {0.06632}&{0.3026}&{0.6864}&{439.43}\\ {0.6969}&{ - 0.5832}&{ - 0.4173}&{ - 1300.8}\\ {0.2730}&{0.7538}&{ - 0.5976}&{ - 1137.5}\\ 0&0&0&1 \end{array}} \right]. $ | (13) |
| $ 0.3288x - 0.4596y + 0.08862z + 1 = 0. $ | (14) |

|
图 7 试验系统图 Fig.7 Diagram of test system |
采集焊缝图像对焊缝初始点进行识别,获得起始点位置的像素坐标为(422.9,317.3),根据标定过程中获得的相机参数求得相机的旋转矩阵Rot
| $ \mathit{\boldsymbol{Rot}} = \left[ {\begin{array}{*{20}{c}} {0.9368}&{ - 0.0452}&{0.3471}\\ { - 0.0452}&{0.9677}&{0.2480}\\ { - 0.3471}&{ - 0.2480}&{0.9044} \end{array}} \right]. $ | (15) |
转换前后的图片对比如图 8(a)和(b)所示,转换后的起始点像素坐标为(328.6,248.3)与摄像机标定所获得的像素中心坐标(334.6,243.1)相差较小,可知该方法可以实现对相机姿态的调整,进而为下一步指导焊枪向起始点靠近做准备.

|
图 8 起始点位置变化 Fig.8 Change of the initial point position: (a) position of the initial point before adjustment; (b) position of the initial point after adjustment; (c) positions of laser and the initial point before approaching; (d) positions of laser and the initial point after approaching |
如图 8(c)所示,激光器发出的十字激光交叉点已出现在摄像机成像平面内,可直接进行精确导引.十字激光交叉点像素坐标为(338.8,355.4),结合转换后的起始点像素坐标以及所标定的激光平面方程,可计算出式(10)所需的已知量,将其代入式(10),求得机器人沿摄像机z轴方向移动的精确值d=144 mm.再将d代入式(8)中,控制机器人沿摄像机光轴(即摄像机坐标系z轴)移动至光点到达焊缝起始点,如图 8(d)所示.最终根据文献[14]中介绍的激光条纹上特征点三维坐标的计算方法,计算出该点的三维坐标,进而控制机器人是焊枪末端到达焊缝起始点.
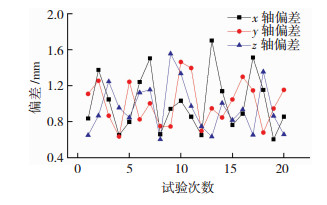
为验证导引方法的有效性,共进行了20次实验,将导引结果的焊缝起始点位置计算值,与通过已标定精确的焊枪末端尖点示教读出的起始点位置进行比较,得出导引结果相对于真实起始点位置的偏差如图 9所示,可知导引精度在0.5~1.6 mm,可满足实际焊接的需要.
|
图 9 试验结果误差图 Fig.9 Chart of test result error |
1) 提出单目视觉与十字激光相结合的两步法,只要保证目标点位于摄像机视野范围内,即可自动完成导引,方法简单、稳定性高.克服了传统基于“单目双位”的立体视觉方法中,匹配算法复杂、导引效率不高等问题.
2) 采用激光点距离图像中心较近、较远两种控制模式对焊枪接近焊接起始点过程进行改进,在获得导引效率的同时又能保证导引精度.
| [1] |
宋天虎, 刘永华, 陈树君. 关于机器人焊接技术的研发与应用之探讨[J]. 焊接, 2016(8): 1-10. SONG Tianhu, LIU Yonghua, CHEN Shujun. The discussion of the technology development and application on the welding robot[J]. Welding & Joining, 2016(8): 1-10. DOI:10.3969/j.issn.1001-1382.2016.08.001 |
| [2] |
陈善本, 林涛. 智能化焊接机器人技术[M]. 北京: 机械工业出版社, 2006. CHEN Shanben, LIN Tao. Intelligent Welding Robot Technology[M]. Beijing: China Machine Press, 2006. |
| [3] |
FANG Z, XU D, TAN M. Vision-based initial weld point positioning using the geometric relationship between two seams[J]. International Journal of Advanced Manufacturing Technology, 2013, 66(9/10/11/12): 1535-1543. |
| [4] |
WANG X, XUE L, YAN Y, et al. Welding robot collision-free path optimization[J]. Applied Sciences, 2017, 7(2): 89. DOI:10.3390/app7020089 |
| [5] |
CHEN Z, WANG J, LI S, et al. An optimized trajectory planning for welding robot[J]. Materials Science and Engineering, 2018, 324(1): 012009. DOI:10.1088/1757-899X/324/1/012009 |
| [6] |
侯震, 许燕玲, 黄色吉, 等. 视觉传感技术在机器人焊接中的应用[J]. 上海交通大学学报, 2016, 50(增刊1): 55-58. HOU Zhen, XU Yanling, HUANG Seji, et al. Application status of vision sensing used in robotic welding[J]. Journal of Shanghai Jiaotong University, 2016, 50(Sup 1): 55-58. DOI:10.16183/j.cnki.jsjtu.2016.S.014 |
| [7] |
SINISTERRA A J, DHANAK M R, ELLENRIEDER K V. Stereovision-based target tracking system for USV operations[J]. Ocean Engineering, 2017, 133: 197-214. DOI:10.1016/j.oceaneng.2017.01.024 |
| [8] |
许仁超, 周方艳, 张启灿. 基于双目视觉的数字散斑时空相关三维面形测量[J]. 激光杂志, 2018, 39(3): 32-36. XU Renchao, ZHOU Fangyan, ZHANG Qican, et al. 3D shape measurement based on binocular vision and digital speckle spatio-temporal correlation[J]. Laser Journal, 2018, 39(3): 32-36. DOI:10.14016/j.cnki.jgzz.2018.03.032 |
| [9] |
陈希章, 陈善本. 弧焊机器人起始焊接位置图像识别与定位[J]. 焊接学报, 2009, 30(4): 17-20. CHEN Xizhang, CHEN Shanben. Arc welding robot initial welding position image recognition and positioning[J]. Transactions of the China Welding Institution, 2009, 30(4): 17-20. DOI:10.3321/j.issn:0253-360X.2009.04.005 |
| [10] |
SHAH H N M, SULAIMAN M, SHUKOR A Z, et al. Butt welding joints recognition and location identification by using local thresholding[J]. Robotics and Computer-Integrated Manufacturing, 2018, 51: 181-188. DOI:10.1016/j.rcim.2017.12.007 |
| [11] |
HAO X, LI W, SUN Z, et al. Detection of ball grid array solder joints based on adaptive template matching[J]. International Journal of Heat & Technology, 2018, 36(1): 189-194. |
| [12] |
熊睿, 马国红, 聂军, 等. 基于多结构元素的形态学焊缝起始点识别[J]. 热加工工艺, 2014, 43(21): 158-160. XIONG Rui, MA Guohong, NIE Jun, et al. Identification of initial welding position in morphology by using multi-structure element[J]. Hot Working Technology, 2014, 43(21): 158-160. |
| [13] |
SICILIANO B, SCIAVICCO L, ORIOLO G. Robotics:Modelling, Planning and Control[M]. NewYork: Springer, 2010.
|
| [14] |
徐德, 王麟琨, 谭民. 基于运动的手眼系统机构光参数标定[J]. 仪器仪表学报, 2005, 26(11): 5-9. XU De, WANG Linkun, TAN Min. A calibration method of structured light stripe for Hand-eye system based on robot movement[J]. Chinese Journal of Scientific Instrument, 2005, 26(11): 5-9. DOI:10.19650/j.cnki.cjsi.2005.11.001 |
| [15] |
TSAI R Y, LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEE Transactions on Robotics & Automation, 1989, 5(3): 345-358. |
 2019, Vol. 27
2019, Vol. 27


